1 Introduction

Hairy black holes are interesting solutions of Einstein’s Theory of Gravity and also of certain types of Modified Gravity Theories. The first attempts to couple a scalar field to gravity was done in an asymptotically flat spacetime finding hairy black hole solutions [1–3] but these solutions violated the no-hair theorems because they were not physically acceptable as the scalar field was divergent on the horizon and stability analysis showed that they were unstable [4]. Then, by introducing a cosmological constant hairy black hole solutions with a minimally coupled scalar field and a self-interaction potential in asymptotically dS space were found, but they were unstable [5, 6]. Also, a hairy black hole configuration was reported for a scalar field non-minimally coupled to gravity [7], but perturbation analysis showed the instability of the solution [8, 9]. In the case of a negative cosmological constant, stable solutions were found numerically for spherical geometries [10, 11] and an exact solution in asymptotically AdS space with hyperbolic geometry was presented in [12] and generalized later to include electric charge [13, 14]. Then a generalization to non-conformal solutions was discussed in [15]. Further hairy solutions in the presence of a cosmological constant were reported in [16–21] with various properties. On the other hand, by introducing a coupling of a scalar field to Einstein tensor that acts as an effective cosmological constant [22, 23] a hairy black hole solution was presented [24], and spherically symmetric hairy black hole solutions with scalar hair were found [25]. Additionally, there are also very interesting recent developments in Observational Astronomy. High precision astronomical observations of the supermassive black holes may pave the way to experimentally test the no-hair conjecture [26]. Also, there are numerical investigations of single and binary black holes in the presence of scalar fields [27], and more recently it was shown that it is not necessary to introduce a cosmological constant to get scalar hairy black holes [28, 29].

On the other hand, the recent developments in string theory and specially the application of the AdS/CFT principle to condensed matter phenomena like superconductivity (for a review see [30]), triggered the interest of further study of the behavior of matter fields outside the black hole horizon [31, 32]. In this context, the gauge/gravity duality is a principle which relates strongly coupled systems to their weak coupled gravity duals. One of the best-studied system is the holographic superconductor. In its simplest form, the gravity sector is a gravitating system with a cosmological constant, a gauge field and a charged scalar field with a potential (for a review see [33]). The dynamics of the system defines a critical temperature above which the system finds itself in its normal phase and the scalar field does not have any dynamics. Below the critical temperature the system undergoes a phase transition to a new configuration. From the gravity side this is interpreted as the black hole to acquire hair while from boundary conformal field theory site this is interpreted as a condensation of the scalar field and the system enters a superconducting phase.

It is well known that all solar system observations, such as light deflection, the perihelion shift of planets, and the gravitational time delay among others, are described within Einstein’s General Relativity. The study of geodesics has been performed under several black hole geometries. For instance, see [34–44] for the motion of particles on AdS spacetime. In this work, motivated by black hole solutions with matter fields outside their horizon, we study their effect in the motion of massless and massive particles in the background of a four-dimensional asymptotically AdS black hole with scalar hair [20]. These hairy black holes solutions are characterized by a self-interacting potential that asymptotically tends to the cosmological constant, and the scalar field is regular everywhere outside the event horizon and null at spatial infinity. The geodesics are studied numerically and we discuss the differences in the motion of particles between the four-dimensional asymptotically AdS black holes with scalar hair and their no-hair limit, that is, Schwarzschild AdS black holes. Also, we study classical tests such as perihelion precession, deflection of light and gravitational time delay in order to determine the contribution that arises from the scalar hair.

The paper is organized as follows. In Sect. 2 we give a brief review of the four-dimensional asymptotically AdS black holes with scalar hair that we will consider as background. In Sect. 3 we study the motion of massless and massive particles, and we perform some classical tests such as perihelion precession, deflection of light and gravitational time delay. Finally in Sect. 4 we conclude.

2 Four-dimensional asymptotically AdS black holes with scalar hair

The hairy black hole that we consider is solution of the Einstein–Hilbert action with a negative cosmological constant and a neutral scalar field minimally coupled to the curvature having a self-interacting potential \( V(\phi )\) [20]. The action is given by

$$\begin{aligned} S=\int \mathrm{d}^{4}x\sqrt{-g}\left( \frac{1}{2 \kappa }R-\frac{1}{2}g^{\mu \nu }\nabla _{\mu }\phi \nabla _{\nu }\phi -V(\phi )\right) , \end{aligned}$$
(1)

the self-interacting potential being

$$\begin{aligned} V\left( \phi \right)= & {} -F\left( 2+\cosh \left( \sqrt{2}\phi \right) \right) + \frac{G}{\nu ^{3}}\left( 6\sinh \left( \sqrt{2}\phi \right) \right. \nonumber \\&\left. -2\sqrt{2}\phi \left( 2+\cosh \left( \sqrt{2}\phi \right) \right) \right) . \end{aligned}$$
(2)

Here, the cosmological constant is incorporated in the potential, that is, \( \Lambda =V(0)\) (\(V(0)<0\)). Here \(\Lambda =-6l^{-2}/\kappa \), l being the length of the AdS space and \(\kappa =8 \pi G_N\), with \(G_N\) the Newton constant. This potential has a global maximum at \(\phi =0\). The equations of motion are

$$\begin{aligned} R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R=\kappa T^{(\phi )}_{\mu \nu }, \end{aligned}$$
(3)

where the energy momentum tensor \(T^{(\phi )}_{\mu \nu }\) for the scalar field is

$$\begin{aligned} T^{(\phi )}_{\mu \nu }=\nabla _{\mu }\phi \nabla _{\nu }\phi - g_{\mu \nu }\left[ \frac{1}{2}g^{\rho \sigma }\nabla _{\rho }\phi \nabla _{\sigma }\phi +V(\phi )\right] ~, \end{aligned}$$
(4)

and the Klein–Gordon equation of the scalar field reads

$$\begin{aligned} \Box \phi =\frac{\mathrm{d} V}{\mathrm{d} \phi }. \end{aligned}$$
(5)

The following metric is a solution of the theory defined by (1):

$$\begin{aligned} \mathrm{d}s^{2}=-f(r)\mathrm{d}t^{2}+f^{-1}(r)\mathrm{d}r^{2}+a^{2}(r)\mathrm{d} \sigma _{k}^2, \end{aligned}$$
(6)

where

$$\begin{aligned} f\left( r\right)= & {} k+Fr\left( r+\nu \right) \nonumber \\&+\frac{G}{\nu ^{3}}\left( -\nu \left( \nu +2r\right) +2r\left( r+\nu \right) \ln \left( \frac{r+\nu }{r} \right) \right) ,\nonumber \\\end{aligned}$$
(7)
$$\begin{aligned} a^{2}(r)= & {} r(r+\nu ), \end{aligned}$$
(8)

and the scalar field is

$$\begin{aligned} \phi \left( r\right) =\frac{1}{\sqrt{2}}\ln \left( 1+\frac{\nu }{r}\right) . \end{aligned}$$
(9)

In Eq. (6), \(\mathrm{d} \sigma _{k} ^2\) is the metric of the spatial 2-section, which can have positive, negative or zero curvature, and the coordinates are defined in the ranges \(0<r<\infty \), \(-\infty <t<\infty \), \(0\le \theta <\pi \), \(0\le \phi <2\pi \). For the lapse function \(k=1,0,-1\) parametrizes the curvature of the spatial 2-sections and F, G are constants being proportional to the cosmological constant and to the mass respectively. It was shown that for spherical horizons \(k=1\) there is no phase transition of the hairy asymptotically AdS black holes to Schwarzschild AdS black hole. However, for hyperbolic horizons \(k=-1\) there exists a phase transition only for negative masses, and the hairy black hole dominates for small temperatures, while for large temperatures the topological black hole would be preferred, for more details see [20].

Fig. 1
figure 1

The behavior of f(r) (top figure), R(r) and \(R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }(r)\) (center figure) and \(R_{\mu \nu }R^{\mu \nu }(r)\) (bottom figure) with \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\)

Full size image

In the next section we perform a numerical analysis of the geodesics by considering the hairy black hole solution. So, without loss of generality, we consider the following values for the parameters: \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\). Thus, in order to show that these parameters yield a hairy black hole solution we plot in Fig. 1 the behavior of the metric function \(f\left( r\right) \), which changes sign for \(r=1.15\), signaling the presence of an horizon. Also we plot the behavior of the Ricci scalar R(r), the principal quadratic invariant of the Ricci tensor \(R^{\mu \nu }R_{\mu \nu }(r)\), and the Kretschmann scalar \(R^{\mu \nu \lambda \tau }R_{\mu \nu \lambda \tau }(r)\), and we observe that there is no Riemann curvature singularity outside the horizon. Also, we observe that the Riemann curvature singularities are covered by the horizon. Therefore, the choice of parameters mentioned above gives a hairy black hole solution which is asymptotically AdS.

3 Geodesics

In order to find the geodesics of the spacetime described by (6), we will solve the Euler–Lagrange equations for the variational problem associated with this metric. The Lagrangian associated to the metric (6) is given by

$$\begin{aligned} 2\mathcal {L}=- f(r)\dot{t}^2+ \frac{\dot{r}^2}{f(r)}+a^2(r)(\dot{\theta }^2+\sin ^2\theta \,\dot{\phi }^2)=-m, \end{aligned}$$
(10)

where \(\dot{q}=\mathrm{d}q/\mathrm{d}\tau \), and \(\tau \) is an affine parameter along the geodesic that we choose as the proper time. Since the Lagrangian (10) is independent of the cyclic coordinates (\(t, \phi \)), their conjugate momenta (\(\Pi _t, \Pi _{\phi }\)) are conserved and the equations of motion read

$$\begin{aligned} \dot{\Pi }_{q} - \frac{\partial \mathcal {L}}{\partial q} = 0, \end{aligned}$$
(11)

where \(\Pi _{q} = \partial \mathcal {L}/\partial \dot{q}\) is the conjugate momentum to the coordinate q. The above equation can be written as

$$\begin{aligned} \dot{\Pi }_{t} = 0, \quad \dot{\Pi }_{r}= & {} -{\dot{t}^{2}\over 2}{\mathrm{d}f(r)\over \mathrm{d}r}+ {\dot{r}^{2}\over 2}{\mathrm{d}f(r)^{-1}\over \mathrm{d}r}\nonumber \\&+a(r){\mathrm{d}a(r)\over \mathrm{d}r}(\dot{\theta } ^{2}+\sin ^{2}\theta \dot{\phi }^2), \end{aligned}$$
(12)
$$\begin{aligned} \dot{\Pi }_{\theta } = a^2(r)\sin \theta \cos \theta \,\dot{\phi }^2, \quad \text {and}\quad \dot{\Pi }_{\phi }=0, \end{aligned}$$
(13)

which yields

$$\begin{aligned} \Pi _{t}= & {} -f(r) \dot{t}, \quad \Pi _{r}= {\dot{r}\over f(r)},\end{aligned}$$
(14)
$$\begin{aligned} \Pi _{\theta }= & {} a^{2}\dot{\theta }, \quad \text {and}\quad \Pi _{\phi } = a^{2}\sin ^{2}\theta \dot{\phi }. \end{aligned}$$
(15)

Now, without loss of generality, we consider the motion to develop in the invariant plane \(\theta = \pi /2\) and \(\dot{\theta }=0\), which is characteristic of the central fields. With this choice, Eqs. (15) and (16) become

$$\begin{aligned} \Pi _{t} = -f(r) \dot{t}\equiv -\sqrt{E}, \quad \Pi _{\phi }= a^{2}\dot{\phi }\equiv L, \end{aligned}$$
(16)

where E and L are dimensionless integration constants associated to each of them. So, inserting Eq. (16) into Eq. (10) we obtain

$$\begin{aligned} \left( \frac{\mathrm{d}r}{\mathrm{d}\tau }\right) ^2=E-V(r), \end{aligned}$$
(17)

where V(r) is the effective potential given by

$$\begin{aligned} V(r)=f(r)\left[ m+\frac{L^2}{r(r+\nu )}\right] , \end{aligned}$$
(18)

where m is the test mass. Finally, by normalization, we shall take \(m=1\) for massive particles and \(m=0\) for photons.

3.1 Time-like geodesic

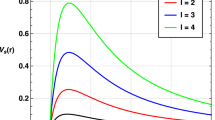
In order to observe the possible orbits, we plot the effective potential for massive particles (18) which is shown in Fig. (2). In the following, we describe the radial motion and the angular motion.

Fig. 2
figure 2

The behavior of V(r) for radial (\(L=7\)) and non-radial (\(L=0\)) particles, with \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\)

Full size image
Fig. 3
figure 3

The behavior of the proper (\(\tau \)) and coordinate (t) time as a function of r, with \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\)

Full size image

3.1.1 Radial motion

In this case \(L=0\). The particles always fall into the horizon from an upper distance determined by the constant of motion \(E=30.88\). This fact is due to the attractive force generated by the proportional term to the cosmological constant; see Fig. 2. In Fig. 3 we plot the proper (\(\tau \)) and coordinate (t) time as a function of r for a particle falling from a finite distance with zero initial velocity, and we can see that the particle falls toward the horizon in a finite proper time. The situation is very different if we consider the trajectory in the coordinate time, where t goes to infinity. This physical result is consistent with the Schwarzschild AdS black hole.

3.1.2 Angular motion

For the angular motion we consider \(L>0\). The allowed orbits depend on the value of the constant E.

  • If \(E=61.6\) the particle can orbit in a stable circular orbit at \(r_s=2.84\); see Fig. 2.

  • If \(E=69.4\) the particle can orbit in an unstable circular orbit at \(r_u=1.518\). Also, there are two critic orbits that approximates asymptotically to the unstable circular orbit. For the first kind, the particle starts from the rest and a finite distance greater than the unstable radio; see Fig. 4. For the second kind, the particle starts from a finite distance greater than the horizon, but smaller than the unstable radio; see Fig. 4.

  • The planetary orbits are constrained to oscillate between an aphelion and a perihelion. We plot in Fig. 5 the planetary orbit for \(E=65\). We can observe that the particle completes an oscillation in an angle less than \(2\pi \), contrary to the Schwarzschild AdS black hole, where the angle is greater than \(2\pi \) [45].

Fig. 4
figure 4

The first (left figure) and second (right figure) kind of critical orbits with \(L=7\), \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\)

Full size image

It is possible to calculate the periods of the circular orbits (\(r_{\mathrm{c.o.}}\)), which can be stable (\(r_\mathrm{s}\)) or unstable (\(r_\mathrm{u}\)) orbits using the constant of motion \(\sqrt{E}\) and L, given by (16), which yields

$$\begin{aligned} T_{\tau }=\frac{2\pi r_{\mathrm{c.o.}}(r_{\mathrm{c.o.}}+\nu )}{L}, \end{aligned}$$
(19)

and

$$\begin{aligned} T_t=\frac{2\pi \sqrt{E}r_{\mathrm{c.o.}}(r_{\mathrm{c.o.}}+\nu )}{L f(r_{\mathrm{c.o.}})}, \end{aligned}$$
(20)

where \(T_{\tau }\) is the period of the orbit with respect to the proper time and \(T_t\) is the period of the orbit with respect to the coordinate time. It is worth to mention that the periods depend on the value of \(\nu \) and in the limit \(\nu \rightarrow 0\) these periods correspond to the periods of the circular orbits in the spacetime Schwarzschild AdS. On the other hand, for the stable circular orbits it is possible to find the epicycle frequency, given by \(\kappa ^2=V''(r_\mathrm{s})/2\).

Fig. 5
figure 5

The planetary orbit with \(L=7\), \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\) for \(E=69.4\)

Full size image

3.1.3 Perihelion precession

Here, we follow the treatment performed by Cornbleet [46], which allows us to derive the formula for the advance of the perihelia of planetary orbits. The starting point is to consider the line element in unperturbed Lorentz coordinates

$$\begin{aligned} \mathrm{d}s^2 = -\mathrm{d}t^2 + \mathrm{d}r^2 + r^2(\mathrm{d}\theta ^2 + \sin ^2 \theta \mathrm{d}\phi ^2), \end{aligned}$$
(21)

together with line element (6). So, considering only the radial and time coordinates in the binomial approximation, the transformation gives

$$\begin{aligned} \mathrm{d}\tilde{t}\approx \left( 1-\frac{G}{6r}+\frac{Fr^2}{2}+\frac{G\nu }{12r^2}+\frac{F\nu r}{2}\right) \mathrm{d}t, \end{aligned}$$
(22)
$$\begin{aligned} \mathrm{d}\tilde{r}\approx \left( 1+\frac{G}{6r}-\frac{Fr^2}{2}-\frac{G\nu }{12r^2}-\frac{F\nu r}{2}\right) \mathrm{d}r. \end{aligned}$$
(23)

We will consider two elliptical orbits, one the classical Kepler orbit in (r, t) space and a hairy AdS orbit in \((\tilde{r},\tilde{t})\) space. Then in the Lorentz space \(\mathrm{d}A = \int _0^{\mathcal {R}}r\mathrm{d}r\mathrm{d}\phi =\mathcal {R}^2\mathrm{d}\phi /2\), and hence

$$\begin{aligned} \frac{\mathrm{d}A}{\mathrm{d}t}=\frac{1}{2}\mathcal {R}^2\frac{\mathrm{d}\phi }{\mathrm{d}t}, \end{aligned}$$
(24)

which corresponds to Kepler’s second law. For the hairy AdS case we have

$$\begin{aligned} \mathrm{d}\tilde{A}=\int _0^{\mathcal {R}}a(r)\mathrm{d}\tilde{r}\mathrm{d}\phi , \end{aligned}$$
(25)

where d\(\tilde{r}\) is given by Eq. (23), and the binomial approximation for the radial function a(r) is

$$\begin{aligned} a(r)\approx r\left( 1+\frac{\nu }{2r}\right) . \end{aligned}$$
(26)

So, we can write (25) as

(27)

Therefore, applying the binomial approximation we obtain

$$\begin{aligned} \frac{ \mathrm{d}\tilde{A}}{\mathrm{d}\tilde{t}}= & {} \frac{\mathcal {R}}{2}\left( 1+\frac{G}{3\mathcal {R}}-\frac{F\mathcal {R}^2}{4}+\frac{\nu }{\mathcal {R}} \right) \frac{\mathrm{d}\phi }{\mathrm{d}\tilde{t}}\nonumber \\\approx & {} \frac{\mathcal {R}}{2}\left( 1+\frac{G}{3\mathcal {R}}-\frac{F\mathcal {R}^2}{4}+\frac{\nu }{\mathcal {R}} \right) \nonumber \\&\times \left( 1+\frac{G}{6\mathcal {R}}-\frac{F\mathcal {R}^2}{2}-\frac{G\nu }{12\mathcal {R}^2}-\frac{F\nu \mathcal {R}}{2}\right) \frac{\mathrm{d}\phi }{\mathrm{d}t}. \end{aligned}$$
(28)

So, we use this increase to improve the elemental angle from d\(\phi \) to d\(\tilde{\phi }\). Then for a single orbit

$$\begin{aligned} \int _0^{\Delta \tilde{\phi }}\mathrm{d}\tilde{\phi }=\int _0^{\Delta \phi =2\pi }\left( 1+\frac{G}{2\mathcal {R}}-\frac{3F\mathcal {R}^2}{4} + \frac{\nu }{\mathcal {R}} \right) \mathrm{d}\phi , \end{aligned}$$
(29)

where we have neglected products of G, F, and \(\nu \). The polar form of an ellipse is given by

$$\begin{aligned} \mathcal {R}=\frac{l}{1+\epsilon \cos \phi }, \end{aligned}$$
(30)

where \(\epsilon \) is the eccentricity and l is the semi-latus rectum. In this way, plugging Eq. (30) into Eq. (29), we obtain

$$\begin{aligned} \Delta \tilde{\phi }= & {} 2\pi +\frac{G}{2}\int _0^{2\pi } \frac{1+\epsilon \cos \phi }{l} \mathrm{d}\phi \nonumber \\&-\frac{3F}{4}\int _0^{2\pi } \left( \frac{l}{1+\epsilon \cos \phi } \right) ^2 \mathrm{d}\phi \nonumber \\&+\,\nu \int _0^{2\pi }\frac{1+\epsilon \cos \phi }{l} \mathrm{d}\phi , \end{aligned}$$
(31)

which at first order yields

$$\begin{aligned} \Delta \tilde{\phi }\approx 2\pi +\frac{\pi G}{l}+\frac{3\pi F l^2}{2} +\frac{2\pi \nu }{l}. \end{aligned}$$
(32)

Therefore, the perihelion advance has the standard value of general relativity plus the correction term coming from cosmological constant and scalar hair. It is worth to mention that there is a (negative) discrepancy between the observational value of the precession of perihelion for Mercury, \(\Delta \tilde{\phi }_{\mathrm{Obs.}}=5599.74\,\mathrm{arcsec/Julian-century}\) and the total \(\Delta \tilde{\phi }_{\mathrm{Total}}= 5603.24\,\mathrm{arcsec/Julian-century}\); see [47]. This may be attributed to the scalar hair correction, given \(\nu = -0.359 \,\mathrm{km}\).

3.2 Null geodesic

In the next analysis, we consider two kinds of motion, for \(L=0\) (radial motion), and \(L>0\) (angular motion) of the photons (\(m=0\)).

3.2.1 Radial motion

In this case, the master equation (17) can be written as

$$\begin{aligned} \frac{\mathrm{d}r}{\mathrm{d}\tau }=\pm \sqrt{E}, \end{aligned}$$
(33)

where (\(+\)) stands for outgoing photons and \((-)\) stands for ingoing photons. The solution of the above equation yields

$$\begin{aligned} r=\pm \sqrt{E} \tau + r_0, \end{aligned}$$
(34)

where \(r_0\) is an integration constant that corresponds to the initial position of the photon, as in the Schwarzschild AdS case. The photons always fall into the horizon from an upper distance determined by the constant of motion \(E=30.88\). In Fig. 6 we plot the proper (\(\tau \)) and coordinate (t) time as a function of r for a photon falling from a finite distance (\(r_0=6\)), we can see that photons fall toward the horizon in a finite proper time. The situation is very different if we consider the trajectory in the coordinate time, where t goes to infinity.

Fig. 6
figure 6

The behavior of the proper (\(\tau \)) and coordinate (t) time for ingoing photons as a function of r, with \(L=0\), \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\)

Full size image

3.2.2 Angular motion

In this case, the allowed orbits for photons depend on the value of the impact parameter \(b\equiv L/\sqrt{E}\). Next, based on the impact parameter values shown in Fig. 7, we give a brief qualitative description of the allowed angular motions for photons, described in the following.

Fig. 7
figure 7

The behavior of the effective potential for photons as a function of r, with \(L=2\), \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\)

Full size image
Fig. 8
figure 8

The first (left figure) and second (right figure) kind of critical orbits with \(L=2\) with \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\) for \(E=5.58\)

Full size image
Fig. 9
figure 9

The deflection of the light with \(L=2\), \(k=1\), \(\nu =-1\), \(F=1\), and \(G=2\) for \(E=5\)

Full size image

  • Capture zone: If \(0< b < b_{u}\), photons fall inexorably to the horizon, and its cross section, \(\sigma \), in this geometry is [48]

    $$\begin{aligned} \sigma =\pi \,b_u^2. \end{aligned}$$
    (35)

  • Critical trajectories: If \(b=b_{u}\) (\(E_u=5.58\)), photons can stay in one of the unstable inner circular orbit of radius \(r_{u}\) (\(r_u=1.5\)). Therefore, the photons that arrive from the initial distance \(r_i\) (\(r_+ < r_i< r_u\), or \(r_u< r_i<\infty \)) can asymptotically fall into a circle of radius \(r_{u}\); see Fig. 8.

  • Deflection zone. If \(b_{u} <b <b_{0}=1/\sqrt{F}\), the photons can fall from infinity to a minimum distance \(r_d=2.09\) and can go back to infinity. This photons are deflected; see Fig. 9. The other allowed orbits correspond to photons moving into the other side of the potential barrier, which plunge into the singularity. In the next section, we will focus on this topic.

3.2.3 Deflection of light

The deflection of light is important because the deflection of light by the Sun is one of the most important tests of general relativity, and the deflection of light by galaxies is the mechanism behind gravitational lenses. The distance of the closest approach, \(r_0\), for the metric (6) can be defined by

$$\begin{aligned} \left( \frac{\mathrm{d}r}{\mathrm{d}\phi }\right) ^2=\frac{a(r)^4}{b^2}-a(r)^2f(r), \end{aligned}$$
(36)

where b is the impact parameter. Now, by using the change of variables \(u=1/r\), the above equation can be written as

$$\begin{aligned} \left( -\frac{\mathrm{d}u}{\mathrm{d}\phi }\right) ^2=\frac{1}{b^2}(1+\nu \, u)^2-(1+\nu \, u)u^2f(u), \end{aligned}$$
(37)

which at first order and applying the binomial approximation wherever necessary leads to

$$\begin{aligned} \left( -\frac{\mathrm{d}u}{\mathrm{d}\phi }\right) ^2=\frac{1}{b^2}-F+ \frac{2\nu \, u}{b^2}-u^2+\left( \frac{G}{3}-\nu \right) u^3. \end{aligned}$$
(38)

Following [49] we define

$$\begin{aligned} y\approx u- \frac{\nu }{b^2}-\frac{1}{2}\left( \frac{G}{3}-\nu \right) u^2. \end{aligned}$$
(39)

So, solving for u yields

$$\begin{aligned} u= \frac{\nu }{b^2}+y+\frac{1}{2}\left( \frac{G}{3}-\nu \right) y^2, \end{aligned}$$
(40)

where we have considered the first order terms. Therefore (38) becomes

$$\begin{aligned} \phi (u)= \int _{(1/b^2-F)^{-1/2}}^\infty \frac{1+\left( \frac{G}{3}-\nu \right) y}{\sqrt{\frac{1}{b^2}-F-y^2}}\mathrm{d}y. \end{aligned}$$
(41)

This can be integrated to give

$$\begin{aligned} \phi _\infty = {\pi \over 2}+\left( \frac{G}{3}-\nu \right) \sqrt{\frac{1}{b^2}-F}, \end{aligned}$$
(42)

and by considering \(\Delta \phi =2\,\phi _\infty -\pi \) (see Fig. 9), it is possible to find the deflection angle accurately, and it reads

$$\begin{aligned} \Delta \phi = 2\left( \frac{G}{3}-\nu \right) \sqrt{\frac{1}{b^2}-F}. \end{aligned}$$
(43)

Therefore, the deflection of light is given by the standard value plus the correction term coming from the cosmological constant (F) and scalar hair (\(\nu \)). It is worth to mention that there is a discrepancy between the theoretical value and the observational value of deflection light measured by Eddington and Dyson in the solar eclipse of March 29, 1919. For the Sobral expedition this value is \(\Delta {\phi }_{\mathrm{Obs.}}= 1.98 \pm 0.16''\), and it is \(\Delta {\phi }_{\mathrm{Obs.}}= 1.61 \pm 0.40''\) for the Principe expedition [50]. Currently, the mean value is \(\Delta {\phi }_{\mathrm{Obs.}}= 1.89\) [51]. So, by attributing this discrepancy to the scalar hair correction and neglecting the contribution from the cosmological constant, one finds \(\nu = -0.386\, \mathrm{km}\), for \(\Delta {\phi }_{\mathrm{Obs.}}= 1.98\), and \(\nu = -0.235\, \mathrm{km}\), for the mean value of \(\Delta {\phi }_{\mathrm{Obs.}}\).

3.2.4 Gravitational time delay

An interesting relativistic effect in the propagation of light rays is the apparent delay in the time of propagation for a light signal passing near the Sun, which is a relevant correction for astronomic observations, and is called the Shapiro time delay. The time delay of Radar Echoes corresponds to the determination of the time delay of radar signals which are transmitted from the Earth through a region near the Sun to another planet or spacecraft and then reflected back to the Earth. The time interval between emission and return of a pulse as measured by a clock on the Earth is

$$\begin{aligned} t_{12}=2\, t(r_1,\rho _0)+2\, t(r_2,\rho _0), \end{aligned}$$
(44)

where \(\rho _0\) is the closest approach to the Sun. Now, in order to calculate the time delay we use (17) and the coordinate time,

$$\begin{aligned} \dot{r}=\dot{t}\,\frac{\mathrm{d}r}{\mathrm{d}t}=\frac{\sqrt{E}}{f(r)}\frac{\mathrm{d}r}{\mathrm{d}t}. \end{aligned}$$
(45)

So, (17) can be written as

$$\begin{aligned} \frac{\sqrt{E}}{f(r)}\frac{\mathrm{d}r}{\mathrm{d}t}=\sqrt{E-\frac{L^2}{a(r)^2}f(r)}. \end{aligned}$$
(46)

By considering \(\rho _0\), the closest approach to the Sun, d\(r/\mathrm{d}t\) vanishes, so that

$$\begin{aligned} \frac{E}{L^2}=\frac{f(\rho _0)}{a(\rho _0)^2}. \end{aligned}$$
(47)

Now, by inserting (47) in (46), the coordinate time which the light requires to go from \(\rho _0\) to r is

$$\begin{aligned} t(r,\rho _0)=\int _{\rho _0}^r \frac{\mathrm{d}r}{f(r)\sqrt{1-\frac{a(\rho _0)^2}{f(\rho _0)}\frac{f(r)}{a(r)^2}}}. \end{aligned}$$
(48)

So, at first order correction we obtain

$$\begin{aligned} t(r, \rho _0)&=\sqrt{r^2-\rho _0^2}+\frac{G}{3}ln\left( \frac{r+\sqrt{r^2-\rho _0^2}}{\rho _0}\right) \nonumber \\&\quad +\frac{1}{2}\left( \frac{G}{3}+\nu \right) \sqrt{\frac{r-\rho _0}{r+\rho _0}}\nonumber \\&\quad -\frac{F}{6}\sqrt{r^2-\rho _0^2}(2r^2+\rho _0^2). \end{aligned}$$
(49)

Therefore, for the circuit from point 1 to point 2 and back, the delay in the coordinate time is

$$\begin{aligned} \Delta t:= & {} 2\left[ t(r_1, \rho _0)+t(r_2,\rho _0)-\sqrt{r_1^2-\rho _0^2}-\sqrt{r_2^2-\rho _0^2}\right] \nonumber \\= & {} t_G+t_F+t_{\nu }, \end{aligned}$$
(50)

where

$$\begin{aligned} t_G= & {} \frac{G}{3}\left[ 2\, \mathrm{ln}\left( \frac{\left( r_1+\sqrt{r_1^2-\rho _0^2}\right) \left( r_2+\sqrt{r_2^2-\rho _0^2}\right) }{\rho _0^2}\right) \right. \nonumber \\&\left. +\sqrt{\frac{r_1-\rho _0}{r_1+\rho _0}}+\sqrt{\frac{r_2-\rho _0}{r_2+\rho _0}}\right] ,\end{aligned}$$
(51)
$$\begin{aligned} t_F= & {} -\frac{F}{6}\left[ \sqrt{r_1^2-\rho _0^2}(2r_1^2+\rho _0^2)+\sqrt{r_2^2-\rho _0^2}(2r_2^2+\rho _0^2)\right] ,\nonumber \\\end{aligned}$$
(52)
$$\begin{aligned} t_\nu= & {} \nu \left( \sqrt{\frac{r_1-\rho _0}{r_1+\rho _0}}+\sqrt{\frac{r_2-\rho _0}{r_2+\rho _0}}\right) . \end{aligned}$$
(53)

For a round trip in the solar system, we have (\(\rho _0<<r_1,r_2\))

$$\begin{aligned} \Delta t \approx \frac{2G}{3}\, \mathrm{ln} \left( \frac{4r_1r_2}{\rho _0}\right) +2\left( \frac{G}{3}+\nu \right) -\frac{F}{3}(r_1^3+r_2^3). \end{aligned}$$
(54)

Therefore, as in the previous cases the time delay has the standard value of general relativity plus the correction term coming from the cosmological constant and scalar hair.

4 Concluding comments

We have considered a four-dimensional asymptotically AdS black hole with scalar hair [20]. These solutions asymptotically give the Schwarzschild anti-de Sitter solution, and they are characterized by a scalar field with a logarithmic behavior, being regular everywhere outside the event horizon and null at spatial infinity, and by a self-interacting potential, which tends to the cosmological constant at spatial infinity. The equations for the geodesics were solved numerically in order to study their behavior. We note that radial motion as a result is found to be equivalent to the Schwarzschild AdS spacetime [45]. Mainly, we have found that it is possible to find bounded orbits like planetary orbits in the background of a four-dimensional asymptotically AdS black holes with scalar hair. However, the periods associated to circular orbits are modified by the presence of the scalar hair. Besides, we have found that some classical tests such as perihelion precession, deflection of light, and gravitational time delay have the standard value of general relativity plus a correction term coming from the cosmological constant and scalar hair. Finally, we found a specific value of the parameter associated to the scalar hair, in order to explain the discrepancy between the theory and the observations, for the perihelion precession of Mercury (\(\nu = -0.359\, \mathrm{km}\)) and light deflection (\(\nu = -0.386\, \mathrm{km}\) for \(\Delta {\phi }_{\mathrm{Obs.}}= 1.98\)). Interestingly, these values are of the same order and sign. In furthering our understanding, it would be interesting to study the motion of massless and massive particles in a charged hairy black hole. Work in this direction is in progress.