1 Introduction

In the 1970s, Bekenstein and Smarr found the Smarr relation for a Kerr–Newman black hole and Hawking proved the existence of black hole radiation. Since then black hole thermodynamics has become an interesting and challenging subject. It turns out that the black hole system has a precise analogy with the non-gravitational thermodynamic system in nature. A black hole not only has a temperature or an entropy, but also it possesses a rich phase structure and admits critical phenomena. Especially, when it comes to AdS spacetimes, there exists a Hawking–Page phase transition between a stable large black hole and a thermal gas which can be explained as the confinement/deconfinement phase transition of a gauge field [1, 2]. This AdS/CFT correspondence [3–5] can be used to study quark–gluon plasmas and various condensed matter phenomena which makes the AdS black hole thermodynamics more attractive.

In the early time, the charged AdS (RN-AdS) black hole was assigned thermodynamical variables such as temperature, entropy, and charge, electric potential, but not volume and pressure. An attempt to introduce the pressure was carried out in Refs. [6, 7]. They rearranged the characters of thermodynamical variables: 1 / T was identified with P, \(r_{+}\) was identified with V, Q was identified with T (where T is the temperature, P is the pressure, \(r_{+}\) is the radius, V is the volume, Q is the charge, for a black hole). This approach is not uniquely defined and mismatches intensive and extensive thermodynamical variables [8]. Recently, treating the variation of the cosmological constant \(\Lambda \) as a pressure has attained increasing attention [8–20]. This interpretation is much more physically sound and avoids the confusion among intensive and extensive variables. What is more, when \(\Lambda \) is identified with the pressure and the black hole mass M is identified with the enthalpy rather than the internal energy, the first law is consistent with the Smarr relation [10].

With this interpretation of the cosmological constant, many works on the AdS black hole phase transition were carried out [21–29]. In Ref. [8], the authors showed that the graph plotted by the state equation of an AdS black hole for fixed T in the P–\(r_{+}\) or P–V plane is reminiscent of the van der Waals (VDW) system. There is an oscillating part of the graph (for \(T<T_{c}\)) which denotes a phase transition. The oscillating part needs to be replaced by an isobar such that the areas above and below it are equal to each other. This treatment is called Maxwell’s equal area law. They also showed that the graph of the Gibbs free energy G (during the phase transition) which possesses a characteristic swallow tail is also reminiscent of the VDW system. What is more, they found the phase transition coexistence line P–T where G and T coincide, they also studied the critical exponents and showed that the results coincide with those of the VDW system. That is why we use the equal area law, which is valid for the VDW system to address the phase transition of an RN-AdS black hole.

As far as we know, there are two ways to obtain the phase diagram or the coexistence line of an AdS black hole: (1) using the Maxwell equal area law, (2) analyzing the characteristic swallow tail behavior of the Gibbs free energy. In this paper, we will use the equal area law to obtain the coexistence line (P–T) and the coexistence surface (P–T–Q) of an RN-AdS black hole. Especially, we use the method which was used in T–S plane (S is the entropy for a black hole) in Ref. [18] to explicitly argue the viewpoint raised in Ref. [30]: that the equal area law can be only used in the P–V, T–S, and \(\phi \)–Q planes, but not in the T–\(r_{+}\) or P–\(\nu \) plane (\(\nu \) is the specific volume defined in Eq. (42)), though for these cases there is also an oscillating behavior below the critical point. Moreover, we obtained the analytical phase transition point relation P–T–Q of an RN-AdS black hole from the P–V plane.

This paper is organized as follows. In Sect. 2, we review the thermodynamical state equation of the RN-AdS black hole in the T–\(r_{+}\) plane. We use the critical point to rescale the state equation and give a brief analysis of the oscillating part. In Sect. 3, we use the equal area law in the T–S, P–V, and P–\(\nu \) planes to obtain the analytical phase transition point relation P–T–Q and discuss the equal area law, the Smarr relation, and the first law. In Sect. 4, we discuss some results and draw conclusions.

2 Thermodynamic state equation of charged AdS black hole and the system’s critical point

The line element of the RN-AdS metric is given as

$$\begin{aligned} \mathrm{d}s^{2}=-F\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{F}+\mathrm{d}\Omega _{2}^{2}, \end{aligned}$$
(1)

where \(\mathrm{d}\Omega _{2}^{2}\) stands for the standard element on \(S^{2}\) and the function F is given by

$$\begin{aligned} F=1-\frac{2M}{r}+\frac{Q^{2}}{r^{2}}+\frac{r^{2}}{l^{2}}. \end{aligned}$$
(2)

The parameter M represents the ADM mass of the black hole, Q represents the total charge, and the AdS curvature radius l is related to the cosmological constant as \(\Lambda =-3/l^2\).

The black hole radius \(r_{+}\), the same as the event horizon position, is determined as the largest root of \(F(r_{+})=0\). The black hole temperature T is given by

$$\begin{aligned} T= & {} \frac{\kappa }{2\pi }=\frac{1}{2\pi }\left( -\frac{1}{2}\sqrt{\frac{g^{11}}{-\hat{g}_{00}}}\hat{g}_{00,1}\right) \nonumber \\= & {} \frac{1}{4\pi {r_{+}}}\left( 1+\frac{3r_{+}^{2}}{l^{2}}-\frac{Q^{2}}{r_{+}^{2}}\right) \end{aligned}$$
(3)

where g is the RN-AdS metric tensor, \(g_{00}\) is the 00 component of the covariant metric tensor g, \(g^{11}\) is the 11 component of the contravariant metric tensor g, and \(\hat{g}_{00}=g_{00}-g^{2}_{03}/g_{33}\). By setting \(T=0\), we can get the extremal RN-AdS black hole as [18]

$$\begin{aligned}&r_{0}^{2}=\frac{l^{2}}{6}\left( \sqrt{1+\frac{12Q^{2}}{l^{2}}}-1\right) ,\nonumber \\&M_{0}=\frac{r_{0}}{3}\left( 2+\sqrt{1+\frac{12Q^{2}}{l^{2}}}\right) . \end{aligned}$$
(4)

In fact, Eq. (3) is the thermodynamic state equation of the black hole and we will frequently use it when we argue about the equal area law. Now we are going to find the critical point and some state information of the RN-AdS black hole from the T–\(r_{+}\) plane. The T–\(r_{+}\) plane is preferred in Ref. [18] because Eq. (3) here is the original thermodynamic state equation, regardless of the thermodynamic quantities P and V. We treat Q as a constant, then T is a function of \(r_{+}\). The critical point occurs when \(T(r_{+})\) has an inflection point,

$$\begin{aligned} \frac{\partial {T}}{\partial {r_{+}}}=0 ,\quad \frac{\partial ^{2}{T}}{\partial {r_{+}^{2}}}=0. \end{aligned}$$
(5)

From the above two equations, we get the critical values (we replace \(\frac{3}{8\pi {l}^{2}}\) by P; this is just for convenience here, but we find in Ref. [10] that P can be treated as the pressure of the AdS black hole system). We write

$$\begin{aligned} r_{c}=\sqrt{6}Q ,\quad \frac{3}{8\pi {l_{c}}^{2}}=\frac{1}{96\pi {Q}^{2}}\equiv {P_{c}},\quad T_{c}=\frac{\sqrt{6}}{18\pi {Q}}. \end{aligned}$$
(6)

From Eq. (6) we can see \(\frac{P_{c}r_{c}}{T_{c}}=\frac{3}{16}\), so we can rescale Eq. (3) to get rid of Q by defining [18]

$$\begin{aligned} r_{+}=\tilde{r}r_{c} ,\quad P=pP_{c} ,\quad T=tT_{c}, \end{aligned}$$
(7)

\(r_{+}\) and \(\tilde{r}\) both are the radius of a black hole—\(\tilde{r}\) is a rescaling of \(r_{+}\).

Then the rescaled equation of T becomes

$$\begin{aligned} t=\frac{3}{4}\left( \frac{1}{\tilde{r}}+\frac{\tilde{r}p}{2}-\frac{1}{6\tilde{r}^{3}}\right) . \end{aligned}$$
(8)

The t–\(\tilde{r}\) graphs for different p are plotted in Fig. 1.

Fig. 1
figure 1

The rescaled t–\(\tilde{r}\) thermodynamical state graph of RN-AdS black hole for different p. The critical point is at \(p=1,\tilde{r}=1,t=1\), which is an inflection point

Full size image

For \(p=1\), there is an inflection point at \(t=1,\tilde{r}=1\), which is just the critical point. For \(p>1\), which is beyond the critical point, the temperature t increases as the radius \(\tilde{r}\) increases. It is a thermally stable “gas” phase black hole (here the term “gas” means that the black hole radius changes largely as the temperature changes just like a gas does, and the term “liquid” means that the black hole radius almost does not change as the temperature changes just like a liquid does). For \(p<1\), which is below the critical point, the t–\(\tilde{r}\) graph is oscillating. There are one maximum point at \((\tilde{r}_{\max },t_{\max })\) and one minimum point at \((\tilde{r}_{\min },t_{\min })\). For \(\tilde{r}<\tilde{r}_{\max }\), the temperature t increases as the radius \(\tilde{r}\) increases, it is a small, thermally stable, near-extremal black hole. For \(\tilde{r}_{\max }<\tilde{r}<\tilde{r}_{\min }\), the temperature t decreases as radius \(\tilde{r}\) increases, it is a thermally unstable black hole. For \(\tilde{r}_{\min }<\tilde{r}\), the temperature t increases as the radius \(\tilde{r}\) increases; it is a large, thermally stable black hole. Inspired by the VDW gas–fluid P–V graph, we can replace the oscillating part of the isopiestic for \(p<1\) by an isobar. For the VDW P–V graph, the isobar should make sure that the areas above and below it are equal to each other, which is called the equal area law. One may say we can use the equal area law here too. In fact, in Ref. [18], one applied the method for the P–\(\nu \) graph. But we find that the equal area law cannot be used here. We will show that the oscillating part should be replaced by an isobar but not the equal area isobar later. Now, we suppose that the oscillating part is replaced by an isobar of which the left hand side is \(\tilde{r}_{l}\) and the right hand side is \(\tilde{r}_{g}\). Just like the VDW case, from right to left, for \(\tilde{r}>\tilde{r}_{g}\) the black hole system is in its “gas” phase, for \(\tilde{r}_{l}<\tilde{r}<\tilde{r}_{g}\) it goes through a phase transition from “gas” phase to the “liquid” phase, for \(\tilde{r}<\tilde{r}_{l}\) it is in the “liquid” phase.

3 Equal area law and phase transition

It was for a first time suggested in Ref. [10] that we may regard the cosmological constant as a variable and treat it as a dynamical pressure of a black hole,

$$\begin{aligned} p=-\frac{1}{8\pi }\Lambda =\frac{3}{8\pi {l^{2}}}. \end{aligned}$$
(9)

With this interpretation, the black hole mass is identified with enthalpy rather than internal energy. Recently, there has been great interest in studying the phase transition of the RN-AdS black hole system in this extended phase space. Based on Ref. [18], we will use the equal area law in the T–S, P–V, and P–\(\nu \) planes to investigate the phase transition in detail.

3.1 Equal area law in T–S plane

The entropy of the black hole system is

$$\begin{aligned} S=\frac{A}{4},\quad A=4\pi {r_{+}^{2}}. \end{aligned}$$
(10)

We can rewrite the thermodynamic state equation as

$$\begin{aligned} T=\frac{1}{4\sqrt{\pi {S}}}\left( 1+8PS-\frac{\pi {Q^{2}}}{S}\right) . \end{aligned}$$
(11)

At the critical point, the entropy is \(S_{c}=\pi {r_{c}^{2}}=6\pi {Q^{2}}\). So, just as the above section, we can rescale \(S=sS_{c}\). Together with the rescaled T and P, the state equation can be written as

$$\begin{aligned} t=\frac{3}{8}\left( p\sqrt{s}+\frac{2}{\sqrt{s}}-\frac{1}{3s^{\frac{3}{2}}}\right) . \end{aligned}$$
(12)

To show the phase transition, t, p should be smaller than the critical point, which means \(t<1\) and \(p<1\). We plot the graph t–s for \(p=0.7615\) in Fig. 2.

Fig. 2
figure 2

The rescaled t–s graph of an RN-AdS black hole for \(p=0.7615\). The oscillating areas above and below the straight line are equal to each other. The equal area law tells us the phase transition point is at \(p=0.7615,t=0.9\)

Full size image

The oscillating part should be replaced by an isobar which satisfies the requirement that the areas above and below it are equal to each other. We suppose the isobar is \(t=t^{*}\), so the left cross point in \(s_{l}\) denotes the “liquid” phase entropy and the right cross point in \(s_{g}\) denotes the “gas” phase entropy. Then the equal area law is manifest as follows:

$$\begin{aligned} t^{*}(s_{g}-s_{l})=\int _{s_{l}}^{s_{g}}t(s)\mathrm{d}s, \end{aligned}$$
(13)

so we obtain

$$\begin{aligned} t^{*}= & {} \frac{1}{\sqrt{s_{g}}+\sqrt{s_{l}}}\left( \frac{3}{2}-\frac{1}{4\sqrt{s_{l}s_{g}}} \right. \nonumber \\&+\left. \frac{p^{*}}{4}(s_{l}+s_{g}+\sqrt{s_{l}s_{g}})\right) . \end{aligned}$$
(14)

Our purpose is to find the coexistence phase transition line for (t, p), thus we just need to solve Eqs. (12) and (14). For Eq. (12), from Fig. 2, the left and right cross points give us two equations. Using \(x=\sqrt{s_{l}},y=\sqrt{s_{g}}\), together with Eq. (14) we have

$$\begin{aligned} t^{*}&=\frac{3}{8}\left( p^{*}x+\frac{2}{x}-\frac{1}{3x^{3}}\right) ,\end{aligned}$$
(15)
$$\begin{aligned} t^{*}&=\frac{3}{8}\left( p^{*}y+\frac{2}{y}-\frac{1}{3y^{3}}\right) ,\end{aligned}$$
(16)
$$\begin{aligned} t^{*}&=\frac{1}{x+y}\left( \frac{3}{2}-\frac{1}{4xy}+\frac{p^{*}}{4}(x^{2}+y^{2}+xy)\right) . \end{aligned}$$
(17)

The equations can be solved straightforwardly. However, it is difficult and complicated. Now we will calculate it in a simpler way.

Equations (15)–(16) \(=\) 0 will give

$$\begin{aligned} x^{2}+y^{2}=-3p^{*}x^{3}y^{3}+6x^{2}y^{2}-xy. \end{aligned}$$
(18)

Setting 2*Eq. (17) = Eqs. (15) + (16) will give

$$\begin{aligned}&p^{*}(x^{2}+y^{2})x^{3}y^{3}-6(x^{2}+y^{2})x^{2}y^{2}+(x^{2}+y^{2})^{2} \nonumber \\&\quad +(x^{2}+y^{2})xy=2p^{*}x^{4}y^{4}-12x^{3}y^{3}+2x^{2}y^{2}. \end{aligned}$$
(19)

Then putting Eq. (18) into Eq. (19) to get rid of \(x^{2}+y^{2}\) and making the replacement \(z=xy\), we have

$$\begin{aligned} {p^{*}}^{2}z^{4}-2p^{*}z^{3}+2z-1=0=z^{2}(p^{*}z-1)^{2}-(z-1)^{2}, \end{aligned}$$
(20)

so we obtain

$$\begin{aligned} z_{1,2}=\pm \frac{1}{\sqrt{p^{*}}},\quad z_{3,4}=\frac{1}{p^{*}}(1\pm \sqrt{1-p^{*}}), \end{aligned}$$
(21)

where \(z_{2}<0\) is meaningless and \(z_{3,4}\) are also unreasonable as \(s_{l}=s_{g}\). So we only have \(z=\frac{1}{\sqrt{p^{*}}}\). Together with Eq. (18), we get

$$\begin{aligned} s_{g,l}&=\frac{1}{2p^{*}}\left( \sqrt{3-\sqrt{p^{*}}}\pm \sqrt{3-3\sqrt{p^{*}}}\right) ^{2},\end{aligned}$$
(22)
$$\begin{aligned} t^{*}&=\sqrt{p^{*}(3-\sqrt{p^{*}})/2}. \end{aligned}$$
(23)

This is the coexistence line of the“gas” and “liquid” phases for the black hole system. We can also rewrite it as

$$\begin{aligned} p^{*}=\left[ 1-2\cos \left( \frac{\mathrm{arccos(}1-{t^{*}}^{2})+\pi }{3}\right) \right] ^{2}. \end{aligned}$$
(24)

Finally, we can rescale back \(P=pP_{c},T=tT_{c}\) to get the phase transition phase as

$$\begin{aligned} T=\sqrt{\frac{8P(3-\sqrt{96\pi {Q^{2}}P)}}{9\pi }}, \end{aligned}$$
(25)

with \(T<T_{c}=\frac{\sqrt{6}}{18\pi {Q}}\) and \(P<P_{c}=\frac{1}{96\pi {Q^{2}}}\). For \(P>P_{c}\), the black hole only exists in its “gas” phase.

3.2 Equal area law in P–V plane

The volume of the black hole is

$$\begin{aligned} V=\frac{4}{3}\pi {r_{+}}^{3}. \end{aligned}$$
(26)

Thus we can rewrite the thermodynamical state equation as

$$\begin{aligned} P=\frac{T}{2}\left( \frac{4\pi }{3V}\right) ^{\frac{1}{3}}-\frac{1}{8\pi }\left( \frac{4\pi }{3V}\right) ^{\frac{2}{3}}+\frac{Q^{2}}{8\pi }\left( \frac{4\pi }{3V}\right) ^{\frac{4}{3}}. \end{aligned}$$
(27)

At the critical point, \(V_{c}=\frac{4}{3}\pi {r_{c}}^{3}=8\sqrt{6}\pi {Q}^{3}\). Thus we can use the same rescaling method \(V=vV_{c}\) together with T, P to rewrite the above state equation

$$\begin{aligned} p=\frac{8t}{3}v^{-\frac{1}{3}}-2v^{-\frac{2}{3}}+\frac{1}{3}v^{-\frac{4}{3}}. \end{aligned}$$
(28)

We plot the p(v) graph in Fig. 3 for \(t=0.9\).

Fig. 3
figure 3

The rescaled p–v graph of RN-AdS black hole for \(t=0.9\). The oscillating areas above and below the straight line are equal to each other. The equal area law tells us the phase transition point is at \(p=0.7615,t=0.9\)

Full size image

The oscillating part should be replaced by an isobar which satisfies the requirement that the areas above and below the isobar are equal to each other. We suppose the isobar is \(p=p^{*}\), the left cross point in \(v_{l}\) denotes the “liquid” phase volume and the right cross point in \(v_{g}\) denotes the “gas” phase volume. Then the equal area law is manifest as follows:

$$\begin{aligned} p^{*}(v_{g}-v_{l})=\int _{v_{l}}^{v_{g}}p(v)\mathrm{d}v, \end{aligned}$$
(29)

so we obtain

$$\begin{aligned} p^{*}= & {} \frac{1}{v_{g}-v_{l}}\left[ 4t^{*}\left( {v_{g}}^{\frac{2}{3}}-{v_{l}}^{\frac{2}{3}}\right) -6\left( {v_{g}}^{\frac{1}{3}}-{v_{l}}^{\frac{1}{3}}\right) \right. \nonumber \\&-\left. \left( {v_{g}}^{-\frac{1}{3}}-{v_{l}}^{-\frac{1}{3}}\right) \right] . \end{aligned}$$
(30)

Using \(x^{3}=v_{l},y^{3}=v_{g}\), from Eqs. (28) and (30), we have

$$\begin{aligned} p^{*}&=\frac{8t^{*}}{3x}-\frac{2}{x^{2}}+\frac{1}{3x^{4}},\end{aligned}$$
(31)
$$\begin{aligned} p^{*}&=\frac{8t^{*}}{3y}-\frac{2}{y^{2}}+\frac{1}{3y^{4}},\end{aligned}$$
(32)
$$\begin{aligned} p^{*}&=\frac{4t^{*}(x+y)-6+\frac{1}{xy}}{x^{2}+xy+y^{2}}. \end{aligned}$$
(33)

Equations (31)–(32) set to 0 will give

$$\begin{aligned} 8t^{*}x^{3}y^{3}-6(x+y)x^{2}y^{2}+(x^{2}+y^{2})(x+y)=0. \end{aligned}$$
(34)

Setting 2*Eq. (33) \(=\) Eqs. (31) + (32) will give

$$\begin{aligned}&24t^{*}(x+y)x^{5}y^{5}-36x^{4}y^{4}+6x^{3}y^{3}=(x^{2}+xy+y^{2})\nonumber \\&\quad \times [8t^{*}(x+y)x^{3}y^{3}-6(x^{2}+y^{2})x^{2}y^{2}+x^{4}+y^{4}].\nonumber \\ \end{aligned}$$
(35)

Equations (34) and (35) can be simplified as

$$\begin{aligned} 2t^{*}x^{2}y^{2}&=x+y,\end{aligned}$$
(36)
$$\begin{aligned} 2{t^{*}}^{2}x^{3}y^{3}-3xy+1&=0. \end{aligned}$$
(37)

According to Eq. (37), we get

$$\begin{aligned} xy= & {} -\frac{\sqrt{2}}{t^{*}}\cos \left( \frac{\theta }{3}\right) ,\quad \frac{\sqrt{2}}{t^{*}}\cos \left( \frac{\theta +\pi }{3}\right) ,\nonumber \\&\frac{\sqrt{2}}{t^{*}}\cos \left( \frac{\pi -\theta }{3}\right) ,\quad \cos (\theta )=\frac{\sqrt{2}}{2}t^{*}. \end{aligned}$$
(38)

Only the last one is correct as xy should be larger than 1. Putting it back into Eq. (36) and using \(\varphi =\frac{\pi -\theta }{3}\), we have

$$\begin{aligned} x= & {} \frac{2}{t^{*}}\cos ^{2}\varphi -\sqrt{\frac{4}{{t^{*}}^{2}}\cos ^{4}\varphi -\frac{\sqrt{2}}{t^{*}}\cos \varphi }, \nonumber \\ y= & {} \frac{2}{t^{*}}\cos ^{2}\varphi +\sqrt{\frac{4}{{t^{*}}^{2}}\cos ^{4}\varphi -\frac{\sqrt{2}}{t^{*}}\cos \varphi }, \nonumber \\ \varphi= & {} \frac{\pi -\theta }{3},\quad \cos \theta =\frac{\sqrt{2}}{2}t^{*}. \end{aligned}$$
(39)

So from Eq. (32) we have

$$\begin{aligned} p^{*}= & {} \frac{8t^{*}}{3y}-\frac{2}{y^{2}}+\frac{1}{3y^{4}}\nonumber \\= & {} \frac{8t^{*}}{3}\Bigg (\sqrt{2}\cos \varphi -\sqrt{2\cos ^{2}\varphi -\frac{t^{*}}{\sqrt{2}\cos \varphi }}\Bigg )\nonumber \\&-2\Bigg (\sqrt{2}\cos \varphi -\sqrt{2\cos ^{2}\varphi -\frac{t^{*}}{\sqrt{2}\cos \varphi }}\Bigg )^{2}\nonumber \\&+\frac{1}{3}\Bigg (\sqrt{2}\cos \varphi -\sqrt{2\cos ^{2}\varphi -\frac{t^{*}}{\sqrt{2}\cos \varphi }}\Bigg )^{4}\nonumber \\= & {} 16\left( \cos \frac{\theta }{3}\cos \frac{\pi +\theta }{3}\right) ^{2}\nonumber \\= & {} \left( 1-2\cos \frac{2(\pi -\arccos \frac{t^{*}}{\sqrt{2}})}{3}\right) ^{2}\nonumber \\= & {} \left( 1-2\cos \frac{\arccos (1-{t^{*}}^{2})+\pi }{3}\right) ^{2}, \end{aligned}$$
(40)

where \(0\le {t^{*}}\le 1\) is just for the physical cases that we are interested in. Now, we have

$$\begin{aligned} t^{*}=\sqrt{p^{*}(3-\sqrt{p^{*}})/2}. \end{aligned}$$
(41)

We find that this result is just the same as Eq. (23). This means the equal area law is identical in the T–S plane and the P–V plane. Thus, we get the analytical result of p(t) or P(T, Q) [rescale p(t) back] for the coexistence line using the P–V equal area law.

3.3 Equal area law in P–\(\nu \) plane

In Refs. [8] and [18], the RN-AdS black hole’s thermodynamical state equation is compared with the VDW equation and the specific volume is identified

$$\begin{aligned} \nu =2l_{p}^{2}r_{+}, \end{aligned}$$
(42)

where \(l_{p}\) denotes the Planck length. In this subsection, we will use the equal area law in P–\(\nu \) plane to get the coexistence line p(t). By setting \(l_{p}=1\), the state equation can be written as

$$\begin{aligned} P=\frac{T}{\nu }-\frac{1}{2\pi {\nu }^{2}}+\frac{2Q^{2}}{\pi {\nu }^{4}}. \end{aligned}$$
(43)

At the critical point, \(\nu _{c}=2\sqrt{6}Q\). We rescale it by \(\nu =\mu \nu _{c}\). Together with the rescaled T, P, we have

$$\begin{aligned} p=\frac{8t}{3\mu }-\frac{2}{\mu ^{2}}+\frac{1}{3\mu ^{4}}. \end{aligned}$$
(44)

We plot the graph in Fig. 4 for \(t=0.9\).

Fig. 4
figure 4

The rescaled p–\(\mu \) graph of the RN-AdS black hole for \(t=0.9\). The oscillating areas above and below the straight line are equal to each other. The equal area law tells us the phase transition point is at \(p=0.751,t=0.9\)

Full size image

The oscillating part should be replaced by an isobar which satisfies the requirement that the areas above and below the isobar are equal to each other. We suppose the isobar is \(p=p^{*}\), the left cross point in \(\mu _{l}\) denotes the “liquid” phase volume and the right cross point in \(\mu _{g}\) denotes the “gas” phase volume. Then the equal area law is manifest as follows:

$$\begin{aligned} p^{*}(\mu _{g}-\mu _{l})=\int _{\mu _{l}}^{\mu _{g}}p(\mu )\mathrm{d}\mu , \end{aligned}$$
(45)

so we obtain

$$\begin{aligned} p^{*}=\frac{1}{\mu _{g}-\mu _{l}}\left( \frac{8t^{*}}{3}\ln \left( \frac{\mu _{g}}{\mu _{l}}\right) +\frac{2}{\mu _{g}}-\frac{2}{\mu _{l}}-\frac{1}{9\mu _{g}^{3}}+\frac{1}{9\mu _{l}^{3}}\right) .\nonumber \\ \end{aligned}$$
(46)

Using \(x=\frac{1}{\mu _{l}},y=\frac{1}{\mu _{g}}\), from Eqs. (44) and (46) we have

$$\begin{aligned} p^{*}&=\frac{8t^{*}}{3}x-2x^{2}+\frac{1}{3}x^{4},\end{aligned}$$
(47)
$$\begin{aligned} p^{*}&=\frac{8t^{*}}{3}y-2y^{2}+\frac{1}{3}y^{4},\end{aligned}$$
(48)
$$\begin{aligned} p^{*}&=\frac{xy}{x-y}\left( \frac{8t^{*}}{3}\ln \frac{x}{y}-2(x-y)+\frac{1}{9}(x^{3}-y^{3})\right) . \end{aligned}$$
(49)

Using the straightforward way, an implicit function of \(p^{*}(t^{*})\) can be obtained. We have

$$\begin{aligned} x_{1}= & {} \sqrt{1+\frac{\Delta }{4}}-\sqrt{2-\frac{\Delta }{4}-\frac{4t^{*}}{\sqrt{4+\Delta }}},\nonumber \\ x_{2}= & {} \sqrt{1+\frac{\Delta }{4}}+\sqrt{2-\frac{\Delta }{4}-\frac{4t^{*}}{\sqrt{4+\Delta }}},\nonumber \\ x_{3}= & {} -\sqrt{1+\frac{\Delta }{4}}-\sqrt{2-\frac{\Delta }{4}+\frac{4t^{*}}{\sqrt{4+\Delta }}},\nonumber \\ x_{4}= & {} -\sqrt{1+\frac{\Delta }{4}}+\sqrt{2-\frac{\Delta }{4}+\frac{4t^{*}}{\sqrt{4+\Delta }}},\nonumber \\ \Delta\equiv & {} \frac{2(1-p^{*})}{A^{\frac{1}{3}}}+2A^{\frac{1}{3}}, \nonumber \\ A\equiv & {} 4{t^{*}}^{2}-3p^{*}-1+\sqrt{(p^{*}-1)^{3}+(1+3p^{*}-4{t^{*}}^{2})^{2}}.\nonumber \\ \end{aligned}$$
(50)

For \(1<x\) and \(0<y<1\), we identify \(x=x_{2}\) and \(y=x_{4}\). Putting them back to Eq. (49), we get an implicit function of \(p^{*}=p^{*}(t^{*})\) as

$$\begin{aligned} p^{*}=\frac{x_{2}x_{4}}{x_{2}-x_{4}}\left[ \frac{8t^{*}}{3}\ln \frac{x_{2}}{x_{4}}-2(x_{2}-x_{4})+\frac{1}{9}({x_{2}}^{3}-{x_{4}}^{3})\right] .\nonumber \\ \end{aligned}$$
(51)

3.4 The Smarr relation and the first law

In the above three subsections, we have got three phase transition coexistence lines for the RN-AdS black hole, while only two lines are identical. However, a thermodynamical system should have only one real phase transition coexistence line, which means the same phase transition point at \(t=0.9\) in Figs. 2, 3, and 4. Unfortunately, the one obtained from the P–\(\nu \) plane is not identical to the other two cases. In the black hole phase transition research, the P–\(\nu \) possibly cannot be used to identify the transition point by the equal area law directly.

We note that in Ref. [30], the authors obtained a numerical result of the phase transition coexistence line by using the second method (analyzing the characteristic swallow tail behavior of the Gibbs free energy). Their fitting formula is (Eq. (45) in their paper)

$$\begin{aligned} \tilde{P}= & {} 0.666902\tilde{T}^{2}+0.175830\tilde{T}^{3}+0.127273\tilde{T}^{4}\nonumber \\&-0.230638\tilde{T}^{5}+0.795846\tilde{T}^{6}-1.36972\tilde{T}^{7}\nonumber \\&+1.47494\tilde{T}^{8}-0.867209\tilde{T}^{9}+0.226773\tilde{T}^{10},\quad \tilde{T}\in (0,1).\nonumber \\ \end{aligned}$$
(52)

The fitting formula displays an overlap with our analytical results Eqs. (24) and (40) in the p–t graph, Fig. 5. This also indicates that the phase transition coexistence line Eq. (51) is wrong.

Fig. 5
figure 5

The phase transition coexistence lines (rescaled p–t graph) for the RN-AdS black hole. Line 1 is from Eqs. (24), (40), and (52), which display an overlap. The former two are obtained by using the equal area law in the T–S plane and the P–V plane, the latter one is obtained by analyzing the characteristic swallow tail behavior of the Gibbs free energy. Line 2 is from Eq. (51) using the equal area law in the P–\(\nu \) plane

Full size image

That is why we emphasize that the equal area law cannot be used in the P–\(\nu \) plane. The equal area law comes from the first law (the differential formula of mass) or the Smarr relation (the integral formula of mass). So the reason originates with the first law or the Smarr relation for the RN-AdS black hole. When the mass, as the original internal energy, is treated as the enthalpy (\(M\equiv {H}\)) of the system [8, 10], the Smarr relation is

$$\begin{aligned} H=2TS-2PV+Q\phi , \end{aligned}$$
(53)

and the first law is

$$\begin{aligned} \mathrm{d}H=T\mathrm{d}S+V\mathrm{d}P+\phi {\mathrm{d}}Q. \end{aligned}$$
(54)

Equation (53) follows from Eq. (54) via integrating a scale transformation. But if P is treated as a constant, then the first law Eq. (54) reduces to a first law without the \(V\mathrm{d}P\) term and the Smarr relation Eq. (53) no longer follows from the first law by the scaling argument. Thus the treatments of the cosmological constant as a variable pressure and the mass as an enthalpy are reasonable.

Then the Gibbs free energy can be obtained as

$$\begin{aligned} \mathrm{d}G=-S\mathrm{d}T+V\mathrm{d}P+\phi {\mathrm{d}}Q. \end{aligned}$$
(55)

During the phase transition, the chemical potential is identical between the two phases. So the Gibbs free energy is unchanged, which means

$$\begin{aligned} -S\mathrm{d}T+V\mathrm{d}P+\phi {\mathrm{d}}Q=0. \end{aligned}$$
(56)

Fixing T and Q, we get

$$\begin{aligned} \int _{P_{g}}^{P_{l}}V\mathrm{d}P=0. \end{aligned}$$
(57)

This gives the equal area law,

$$\begin{aligned} P(V_{g}-V_{l})=\int _{V_{l}}^{V_{g}}P(V)\mathrm{d}V. \end{aligned}$$
(58)

By fixing P and Q, or T and P, we get the other two equal area laws in the T–S and Q–\(\phi \) planes [18, 31]. The equal area law is right only for special planes rather than any kind of oscillating lines (such as the T–r plane in Fig. 1 or the P–\(\nu \) plane). For the P–V plane, the V is the volume of the black hole rather than the specific volume \(\nu \). That is why the equal area law cannot be used in the P–\(\nu \) plane. So far, we have explicitly checked that the equal area law cannot be used in the P–\(\nu \) plane by comparing the p–t phase transition graphs obtained by using the equal area law in the T–S, P–V, P–\(\nu \) planes and by analyzing the characteristic swallow tail behavior of the Gibbs free energy, and it is also checked from the Smarr equation.

4 Discussion and conclusion

The equal area law is investigated for a black hole phase transition. For the especial case of an RN-AdS black hole, we argued that the equal area law can be only used in the P–V, T–S, and \(\phi \)–Q planes. Though in the T–r or P–\(\nu \) plane there is an oscillating behavior below the critical point, the equal area isobar cannot be used to replace the oscillating part. To address this argument, first of all, we make the assumption that the equal area law holds for any state graph which possesses an oscillating behavior. Then we have obtained the phase transition points (an analytical relation between T, P, Q) by using the equal area law in the T–S, P–V, P–\(\nu \) planes. The result shows that the phase diagrams obtained from the T–S, P–V planes are identical but they are different from the one obtained from the P–\(\nu \) plane. There should be only one phase diagram for a thermodynamical system, so the phase diagram obtained from the P–\(\nu \) plane is wrong, contradicting our assumption. We have also made a comparison of our results with the fitting formula Eq. (52) obtained in Ref. [30], which indicates that the phase diagram obtained from the P–\(\nu \) plane is wrong. To further understand why the equal area law cannot be used in these planes, we traced back the derivation of the equal area law and found that the Smarr relation or the first law, which guarantees the equal area law, can only be used in the P–V, T–S, and \(\phi \)–Q planes.

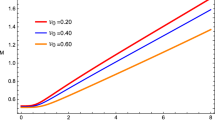
In Sects. 3.1 and 3.2, we get the analytical T–P–Q phase transition relation. With this analytical phase transition relation, it is convenient to analyze the phenomena near the critical point. The graph is plotted in Fig. 6.

Fig. 6
figure 6

The phase transition coexistence surface (T–P–Q graph) for the RN-AdS black hole. The phase transition line of P–T decreases as the charge Q increases, the pressure P increases as the temperature T increases

Full size image

We see that the RN-AdS black hole’s P–T coexistence line for fixed charge Q is just the same as the VDW case: as the temperature T increases in the smaller T region, the corresponding pressure P increases very slowly, while in the bigger T region, P increases quickly as T increases. The critical points are very different for different Q; the critical point quickly decreases as the Q increases. This means that the condition for a highly charged RN-AdS black hole to transit from its “gas” phase to a “liquid” phase is very difficult to reach, which requires a very low temperature.

The RN-AdS black hole system is reminiscent of the VDW system in many aspects, except for the specific volume. For the VDW case, the equal area law can be used in the P–\(\nu \) plane. The specific volume is \(\nu =\frac{V}{Nm}\sim \frac{V}{N}\), here N stands for the molecule number in V and m stands for the molecule mass. The molecule mass is a constant, so the specific volume can stand for one molecule’s volume. This means the specific volume gives us microscopic information of the VDW system. We may expect that the specific volume of the black hole can give us some microscopic information too. The different specific volume between a RN-AdS black hole system and a VDW system probably means there are different microscopic structures.