1 Introduction

It is well known that the Tsallis distribution gives excellent fits to the transverse momentum distributions observed at the Relativistic Heavy Ion Collider (RHIC) [1–3] and at the Large Hadron Collider (LHC) [4–8] with only three parameters, q, T, and dN / dy (or, alternatively, a volume V [9–11]). The parameter q is referred to as the Tsallis parameter and discussed elsewhere [12] in detail. The parameter T obeys the standard thermodynamic relation,

$$\begin{aligned} \left. T = \frac{\partial E}{\partial S}\right| _{N, V}, \end{aligned}$$

however, the entropy used in the above equation is the Tsallis entropy [13], not the standard Boltzmann–Gibbs (BG) entropy. The parameter V is not necessarily related to a volume deduced from other models like HBT calculations.

It was recently shown that these fits extend to values [14] of \(p_T\) up to 200 GeV/c [15, 16]. This is unexpected because in this kinematic range hard scattering processes become important [17]. A description of the high \(p_T\) results has been discussed in [18] where a model using a combination of Tsallis at low \(p_T\) and QCD hard scattering at high \(p_T\) was considered. The present analysis shows that the Tsallis distribution describes measurements up to the highest \(p_T\) using the same Tsallis parameters as those obtained at low \(p_T\).

A power law based on the Tsallis distribution [13] is used to fit the \(p_T\) spectra of charged particles measured by the ATLAS and CMS collaborations. The ATLAS collaboration has reported the transverse momentum in an inclusive phase space region taking into account at least two charged particles in the kinematic range \(|\eta | < 2.5\) and \(p_T > 100\) MeV [7]. The CMS collaboration has presented the differential transverse momentum distribution covering a \(p_T\) range up to 200 GeV/c, the largest range ever measured in a colliding beam experiment [14]. The results for the charged particle multiplicities are consistent with those of ATLAS measurements.

Moreover, the results are compared with those obtained in [15–17, 19, 20] where very good fits to transverse momentum distributions were presented. We confirm the quality of the fits but obtain different values of the parameters albeit using a different version of the Tsallis model.

2 Tsallis distribution

Power law distributions have been widely applied in high energy physics [1–8] to describe the transverse momentum spectra of secondary particles produced in proton–proton collisions. With the advent of the LHC, transverse momenta of hundreds of GeV have been measured. It is of great interest to choose a distribution which describes such high \(p_T\) measurements very well. A well-suited form of the Tsallis distribution is discussed in this paper and our main criterion for choosing such a distribution was thermodynamic consistency, which has not always been implemented fully [21–23].

It is well established that there are numerous physical systems under which BG statistics encounters many difficulties. In particular, when analyzing the \(p_T\) spectra of hadrons it is found that spectra decrease far slower than predicted by BG statistics, and they appear to follow some power law at high \(p_T\). The Tsallis distribution was first proposed about 27 years [13] ago as a generalization of the BG distribution.

The Tsallis form of the BG distribution is given by

$$\begin{aligned} f(E) \equiv \exp _{q}\left( -\frac{E-\mu }{T}\right) , \end{aligned}$$
(1)

where E is the energy and \(\mu \) is the chemical potential and the function \(\exp _{q}(x)\) is usually defined as

(2)

in the limit where \(q \rightarrow 1\) it reduces to the standard exponential:

$$\begin{aligned} \lim _{q \rightarrow 1} \exp _q(x) \rightarrow \exp (x). \end{aligned}$$

The expressions of the relevant thermodynamic quantities like entropy, S, energy density, \(\epsilon (= E/V)\), pressure, P, and particle number, N, are given below using the q-logarithm function,

$$\begin{aligned} \ln _q(x) \equiv \frac{x^{1-q} - 1}{1 - q}, \end{aligned}$$

as integrals over the function defined in Eq. (1) [11, 22, 23]:

$$\begin{aligned}&S = - gV\int \frac{\mathrm{d}^3p}{(2\pi )^3}\left[ f^{q}\ln _{q}f - f\right] ,\end{aligned}$$
(3)
$$\begin{aligned}&\epsilon = g\int \frac{\mathrm{d}^3p}{(2\pi )^3}~E~f^{q},\end{aligned}$$
(4)
$$\begin{aligned}&P = g\int \frac{\mathrm{d}^3p}{(2\pi )^3}\frac{p^{2}}{3E}~f^{q},\end{aligned}$$
(5)
$$\begin{aligned}&N = gV\int \frac{\mathrm{d}^3p}{(2\pi )^3} f^{q} , \end{aligned}$$
(6)

where g is the degeneracy factor and V is the volume. The Tsallis distribution used in this paper is thermodynamically consistent, which means that the following relations, derived from the differential form of the first and second laws of thermodynamics, are satisfied [23]:

$$\begin{aligned} T&= \left. \frac{\partial \epsilon }{\partial s}\right| _n,\quad \mu = \left. \frac{\partial \epsilon }{\partial n}\right| _s, \nonumber \\ n&= \left. \frac{\partial P}{\partial \mu }\right| _T, \quad s = \left. \frac{\partial P}{\partial T}\right| _\mu , \end{aligned}$$
(7)

where s and n are the entropy and particle number densities respectively.

The corresponding momentum distribution deduced from Eq. (6) is given by

$$\begin{aligned} E \frac{\mathrm{d}^{3}N}{dp^3} = gVE \frac{1}{(2\pi )^3}\left[ 1 + (q-1)\frac{E-\mu }{T}\right] ^{-\frac{q}{q-1}}, \end{aligned}$$
(8)

which in terms of the rapidity, y, and transverse mass, \(m_T\), variables (\(E = m_{T}\cosh y\)) at mid-rapidity and for \(\mu = 0\) becomes [11, 22]

$$\begin{aligned} \left. \frac{\mathrm{d}^{2}N}{\mathrm{d}p_{T}\mathrm{d}y}\right| _{y = 0} = gV\frac{p_{T}m_{T}}{(2\pi )^2}\left[ 1 + (q - 1) \frac{m_T}{T}\right] ^{-\frac{q}{q-1}}. \end{aligned}$$
(9)

The relationship between the above parameterization and the one used by the RHIC and LHC collaborations [1–8] has been discussed in [9].

Additionally, a comparison with high-energy data has been made in [15–17, 19, 20], using a simplified form:

$$\begin{aligned} \left. \frac{\mathrm{d}^{2}N_{ch}}{\mathrm{d}p_T\mathrm{d}y}\right| _{y = 0} = A\left[ 1 + (q - 1)\frac{p_T}{T}\right] ^{-\frac{1}{q - 1}} \end{aligned}$$
(10)

where A is a normalization factor and T is a parameter used to fit the transverse momentum distribution and not related to the temperature in the thermodynamic sense as in Eq. (9).

Furthermore, integration of Eq. (9) over the transverse momentum leads to [10]

$$\begin{aligned} \left. \frac{\mathrm{d}N}{\mathrm{d}y}\right| _{y = 0}&= \frac{gV}{(2\pi )^2} \int _0^\infty p_{T}\mathrm{d}p_{T}m_{T} \left[ 1 + (q - 1) \frac{m_T}{T}\right] ^{-\frac{q}{q-1}}\nonumber \\&= \frac{gVT}{(2\pi )^2} \left[ \frac{(2 - q)m^{2} + 2mT + 2T^{2}}{(2 - q)(3 - 2q)}\right] \nonumber \\&\quad \times \left[ 1 + (q - 1) \frac{m}{T}\right] ^{-\frac{1}{q-1}}, \end{aligned}$$
(11)

where m is the rest mass.

Using the values of parameters q, T, and V obtained from Tsallis fit, using Eq. (9), the above equation enables us to obtain the values of \(\mathrm{d}N/\mathrm{d}y\) for pions, kaons, and protons. Their sum gives the values of \(\mathrm{d}N/\mathrm{d}y\) for charged particles.

3 Fit details

The charged particle transverse momentum spectra measured by the ATLAS and CMS detectors in proton–proton collisions at LHC energies are fitted using Eq. (9).

It is well established that the charged particle \(p_T\) spectra is composed of contribution from pions, kaons, and protons. Hence, a sum of three Tsallis distributions for pions, \(\pi ^{+}\)’s, kaons, \(K^{+}\)’s, and protons, p, has been applied to fit the charged particle \(p_T\) spectra in the following way:

$$\begin{aligned} \left. \frac{\mathrm{d}^2N_{ch}}{\mathrm{d}p_T\mathrm{d}y}\right| _{y = 0}&= 2p_T\frac{V}{(2\pi )^{2}}\sum _{i = 1}^3g_{i}m_{T,i}\nonumber \\&\quad \times \left[ 1 + (q - 1) \frac{m_{T,i}}{T}\right] ^{-\frac{q}{q-1}} \end{aligned}$$
(12)

where \(i = \pi ^{+}, K^{+}, p\). The additional factor of 2 on the right-hand side of Eq. (12) takes into account the negatively charged particles \(\pi ^{-}, K^{-}, \bar{p}\). The relative weights between particles were determined by the corresponding degeneracy factors and are given by \(g_{\pi ^{+}} = g_{K^{+}} = 1\) and \(g_p = 2\). The square root of the sum of the squares of the statistical and systematic errors (quadrature) was taken into account for fitting the data.

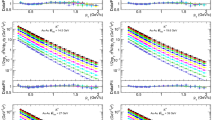
The charged particle multiplicity as a function of the transverse momentum measured by the ATLAS collaboration for events with \(n_{ch} \ge 2\), \(p_T > 100\) MeV and \(|\eta | < 2.5\) at \(\sqrt{s} = 0.9\) and 7 TeV in proton–proton collisions are shown in Fig. 1. The parameterization given in Eq. (12) has been used to fit the spectra. In order to show the quality of the fits in more detail, Fig. 2 shows the ratios of the data to the fit values at \(\sqrt{s} = 0.9\) and 7 TeV for the ATLAS data. The largest deviations occur at the lower energy 0.9 TeV, while the 7 TeV data show deviations from the Tsallis fits which are at most in the 10 % range.

Fig. 1
figure 1

Charged particle multiplicities as a function of the transverse momentum measured by the ATLAS detector for events with \(n_{ch} \ge 2\), \(p_T > 100\) MeV and \(|\eta | < 2.5\) at \(\sqrt{s} = 0.9\) and 7 TeV in proton–proton collisions [7] fitted with a Tsallis distribution

Full size image
Fig. 2
figure 2

Ratios of the data to the fit values measured by the ATLAS detector at \(\sqrt{s} = 0.9\) and 7 TeV

Full size image

The charged particle differential transverse momentum yields in proton–proton collisions at \(\sqrt{s} = 0.9\) and 7 TeV have been measured within \(|\eta | < 2.4\) by the CMS detector. The CMS measurements are described by the Tsallis fit and displayed in Fig. 3. The ratios of the data to the Tsallis fit at \(\sqrt{s} = 0.9\) and 7 TeV are shown in Fig. 4. Again, in order to show the quality of the fits in more detail, Fig. 4 shows the ratios of the data to the fit values at \(\sqrt{s} = 0.9\) and 7 TeV for the CMS data. The largest deviations occur at the highest values of \(p_T\), where also the error bars are largest.

Fig. 3
figure 3

Charged particle differential transverse momentum yields measured within \(|\eta | < 2.4\) by the CMS detector in proton–proton collisions at \(\sqrt{s} = 0.9\) and 7 TeV [14] fitted with a Tsallis distribution

Full size image
Fig. 4
figure 4

Ratios of the data to the fit values measured by the CMS detector at \(\sqrt{s} = 0.9\) and 7 TeV

Full size image

4 Results and discussions

A thermodynamically consistent form of the Tsallis distribution, given in Eq. (9), has been used to fit the transverse momentum spectra of the charged particle measured by both ATLAS and CMS collaborations in proton–proton collisions at \(\sqrt{s} = 0.9\) and 7 TeV. It is observed from Figs. 1 and 3 that the Tsallis distribution fits well the measured \(p_T\) spectra, albeit that the kinematical conditions of the data of both detectors were not identical. It is clear that the proposed form of the Tsallis distribution fits not only the low \(p_T\) but covers a wide range of \(p_T\) spectra up to 200 GeV/c.

The ratios of the experimental data over the fit values, depicted in Figs. 2 and 4, show an intriguing log-periodic oscillation as a function of the transverse momentum not only for high \(p_T\) data sets [14] but also for low \(p_T\) data sets [7]. This was first noticed in [19, 20] for CMS data sets only. The origin of such oscillations is a matter of investigation aiming to draw some useful physics out of it.

The values of the fit parameters, q, T, and the corresponding \(\chi ^2/NDF\) obtained from the fits of the \(p_T\) spectra are given in Table 1. For the highest values of \(p_T\), reaching 200 GeV/c, a value of \(\chi ^2/NDF\approx 0.52/24\) for the CMS data is obtained.

Table 1 Values of the q, T, and R parameters and \(\chi ^2/NDF\) obtained using Eq. (9) to fit the \(p_T\) spectra measured by the ATLAS [7] and CMS [14] detectors
Full size table

Instead of parameter V, a parameter \(R \equiv [V \frac{3}{4\pi }]^{1/3}\), referred to as radius, is listed in the table. It has been found that the value of q increases slowly but clearly with increase in the center-of-mass energy. The thermodynamically consistent version leads to a temperature \(T \approx 75\) MeV at both values of \(\sqrt{s}\). It can be observed that the parameter \(R \approx 4.5\) and 5.0 fm for \(\sqrt{s} = 0.9\) and 7 TeV, respectively, for both ATLAS and CMS data sets. These results are in agreement with the previous analysis done for lower \(p_T\) data [9, 11].

Table 2 shows the values of \(\left. \frac{\mathrm{d}N}{\mathrm{d}y}\right| _{y=0}\) for pions, kaons, protons, and total charged particles evaluated using Eq. (11). The \(\left. \frac{\mathrm{d}N_{ch}}{\mathrm{d}\eta }\right| _{\eta =0}\) values measured by the ATLAS detector is also present. It can be found that the production of pions is less and more kaons and protons are produced at higher energies. The charged particle multiplicity found for ATLAS using a Tsallis fit is close to the measured values. An estimate of the charged particle multiplicity is presented for CMS, which can be verified by the CMS collaboration.

Table 2 Values of \(\left. \frac{\mathrm{d}N}{\mathrm{d}y}\right| _{y=0}\) for pions, kaons, protons, and total charged particles obtained using Eq. (11) and \(\left. \frac{\mathrm{d}N_{ch}}{\mathrm{d}\eta }\right| _{\eta =0}\) measured by ATLAS detector
Full size table

5 Conclusions

We find it quite remarkable that the transverse momentum distributions measured up to 200 GeV/c in \(p_T\) can be described consistently over 14 orders of magnitude by a straightforward Tsallis distribution as presented in Eq. (12). The values of \(\chi ^2/NDF\) are listed in Table 1 and for the highest values of beam energy and \(p_T\) it is found to be 0.52/24 for the CMS data. The distribution used is part of a consistent thermodynamic description satisfying the basic consistency conditions given in Eq. (7).

In conclusion, we have shown that the proposed version of the Tsallis distribution fits the transverse momentum spectra with minimal values of \(\chi ^2\) values, and an estimate of the particle multiplicities and particle ratio has been obtained.