Higgs decays into charginos and neutralinos in the complex MSSM: a full one-loop analysis

Abstract

For the search for additional Higgs bosons in the minimal supersymmetric standard model (MSSM) as well as for future precision analyses in the Higgs sector a precise knowledge of their decay properties is mandatory. We evaluate all two-body decay modes of the Higgs bosons into charginos and neutralinos in the MSSM with complex parameters (cMSSM). The evaluation is based on a full one-loop calculation of all decay channels, also including hard QED radiation. We restricted ourselves to a version of our renormalization scheme which is valid for $|M_1| < |M_2|, |\mu |$ and $M_2 \ne \mu$ to simplify the analysis, even though we are able to switch to other parameter regions. The dependence of the Higgs boson predictions on the relevant cMSSM parameters is analyzed numerically. We find sizable contributions to many partial decay widths. They are roughly of 10 % of the tree-level results, but they can go up to 20 % or higher. The full one-loop contributions are important for the correct interpretation of heavy Higgs boson search results at the LHC and, if kinematically allowed, at a future linear $e^+e^-$ collider. There are plans to implement the evaluation of the branching ratios of the Higgs bosons into the Fortran code FeynHiggs, together with an automated choice of the renormalization scheme valid for the full cMSSM parameter space.

1 Introduction

One of the most important tasks at the LHC is to search for physics effects beyond the standard model (SM), where the minimal supersymmetric standard model (MSSM) [1–4] is one of the leading candidates. Supersymmetry (SUSY) predicts two scalar partners for all SM fermions as well as fermionic partners to all SM bosons. Another important task of the LHC is the investigation of the mechanism of electroweak symmetry breaking. The most frequently studied realizations are the Higgs mechanism within the SM and within the MSSM. Contrary to the case of the SM, in the MSSM two Higgs doublets are required. This results in five physical Higgs bosons instead of the single Higgs boson in the SM. In lowest order these are the light and heavy ${\mathcal CP}$-even Higgs bosons, $h$ and $H$, the ${\mathcal CP}$-odd Higgs boson, $A$, and two charged Higgs bosons, $H^\pm$. Within the MSSM with complex parameters (cMSSM), taking higher-order corrections into account, the three neutral Higgs bosons mix and result in the states $h_i$ ($i = 1,2,3$) [5–9]. The Higgs sector of the cMSSM is described at the tree level by two parameters: the mass of the charged Higgs boson, $M_{H^{\pm }}$, and the ratio of the two vacuum expectation values, $\tan \beta \equiv t_\beta = v_2/v_1$. Often the lightest Higgs boson, $h_1$, is identified with the particle discovered at the LHC [10, 11] with a mass around $\sim$ $125\, \mathrm {GeV}$. If the mass of the charged Higgs boson is assumed to be larger than $\sim$ $200\, \mathrm {GeV}$ the four additional Higgs bosons are roughly mass degenerate, $M_{H^{\pm }}\approx m_{h_{2}} \approx m_{h_{3}}$, and they are referred to as the “heavy Higgs bosons”. Discovering one or more of those additional Higgs bosons would be an unambiguous sign of physics beyond the SM and could yield important information as regards their possible supersymmetric origin.

If SUSY is realized in nature and the charged Higgs-boson mass is $M_{H^{\pm }}\lesssim 1.5\, \mathrm {TeV}$, then the heavy Higgs bosons could be detectable at the LHC [12, 13] (including its high luminosity upgrade, HL-LHC; see Ref. [14] and references therein) and/or at a future linear $e^+e^-$ collider such as the ILC [15–19] or CLIC [20, 21]. (Results on the combination of LHC and ILC results can be found in Refs. [22–24].) The discovery potential at the HL-LHC goes up to $\mathcal{O}(1\, \mathrm {TeV})$ for large $\tan \beta$ values and somewhat lower at low $\tan \beta$ values. At an $e^+e^-$ linear collider the heavy Higgs bosons are pair produced, and the reach is limited by the center-of-mass energy, $M_{H^{\pm }}\lesssim \sqrt{s}/2$, roughly independent of $\tan \beta$. Details as regards the discovery process(es) depend strongly on the cMSSM parameters (and they will not be further discussed in this paper).

In the case of the discovery of additional Higgs bosons a subsequent precision measurement of their properties will be crucial to determine their nature and the underlying (SUSY) parameters. In order to yield a sufficient accuracy, one-loop corrections to the various Higgs-boson decay modes have to be considered. Decays to SM fermions have been evaluated at the full one-loop level in the cMSSM in Ref. [25]; see also Ref. [26] as well as Refs. [27–32] for higher-order SUSY corrections. Decays to (lighter) Higgs bosons have been evaluated at the full one-loop level in the cMSSM in Ref. [25]; see also Refs. [33, 34]. Decays to SM gauge bosons (see also Ref. [35]) can be evaluated to a very high precision using the full SM one-loop result [36–38] combined with the appropriate effective couplings [39]. The full one-loop corrections in the cMSSM listed here together with resummed SUSY corrections have been implemented into the code FeynHiggs [39–44]. Corrections at and beyond the one-loop level in the MSSM with real parameters (rMSSM) are implemented into the code HDECAY [45–47]. Both codes were combined by the LHC Higgs Cross Section Working Group to obtain the most precise evaluation for rMSSM Higgs boson decays to SM particles and decays to lighter Higgs bosons [48].

The (heavy) MSSM Higgs bosons can (if kinematically allowed) also decay to SUSY particles, i.e. to charginos, neutralinos and scalar fermions. In Ref. [49] it was demonstrated that the SUSY particle modes can dominate the decay of the heavy Higgs bosons. The lightest neutral Higgs boson, on the other hand, may have a substantial branching ratio into the lightest neutralino, $h_1 \rightarrow \tilde{\chi }_{1}^0\tilde{\chi }_{1}^0$, where the $\tilde{\chi }_{1}^0$ constitutes the dark matter candidate in the MSSM [50, 51]. Bounds on $m_{\tilde{\chi }_{1}^0}$ often assume an underlying SUSY grand unified theory, based on a simple Lie group. Dropping these assumptions, hardly any bound on $m_{\tilde{\chi }_{1}^0}$ can be placed directly (see, e.g., Ref. [52] and references therein), and the decay $h_1 \rightarrow \tilde{\chi }_{1}^0\tilde{\chi }_{1}^0$ is kinematically possible. In order to determine the dark matter properties a precision measurement of this process at the LHC or a future $e^+e^-$ collider will be necessary.

Higher-order contributions to MSSM Higgs boson decays to scalar fermions have been evaluated in various analyses over the last decade. For calculations in the rMSSM, see Refs. [53–55] and references therein. More recently, the results of Ref. [53] were made public in the code HFOLD [56], using a pure ${\overline{\mathrm {DR}}}$ renormalization for the calculation. In Ref. [57] the $\mathcal{O}(\alpha _s)$ corrections to Higgs boson decays to scalar quarks were re-analyzed and included into the code HDECAY. Within the cMSSM a full one-loop calculation of Higgs boson decays to scalar fermions has recently been published in Ref. [58] and will be included into the code FeynHiggs. These results were obtained in a renormalization scheme [39, 59–65] which has been shown to yield stable results over nearly the full cMSSM parameters space. In this work we take another step in the direction of completion of the calculation of all two-body decays at the one-loop level in the cMSSM in this stable and reliable renormalization scheme: we calculate all two-body decay modes of the Higgs bosons to charginos and neutralinos in the cMSSM. More specifically, we calculate the full one-loop corrections to the partial decay widths

$$\begin{aligned}&\Gamma (h_i \rightarrow \tilde{\chi }_{c}^- \tilde{\chi }_{c^\prime }^+)&\quad&(i = 1,2,3;\, c,c^\prime = 1,2), \end{aligned}$$

(1)

$$\begin{aligned}&\Gamma (h_i \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{n^\prime }^0)&\quad&(i = 1,2,3;\, n,n^\prime = 1,2,3,4), \end{aligned}$$

(2)

$$\begin{aligned}&\Gamma (H^\pm \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{c}^\pm )&\quad&(n = 1,2,3,4;\, c = 1,2), \end{aligned}$$

(3)

where $\tilde{\chi }_{c}^\pm$ ($\tilde{\chi }_{n}^0$) denotes the charginos (neutralinos). While we have calculated the decay of all Higgs bosons, in the numerical evaluation below, we will concentrate on the heavy Higgs bosons, $h_{2,3}$ and $H^\pm$, but also show results for $h_1 \rightarrow \tilde{\chi }_{1}^0\tilde{\chi }_{1}^0$.

The evaluation of the channels Eqs. (1)–(3) is based on a full one-loop calculation, i.e. including electroweak corrections, as well as soft and hard QED radiation. For “mixed” decay modes, we evaluate in addition the two “${\mathcal CP}$-versions” $(c \ne c^\prime )$ of Eq. (1) and the two “${\mathcal CP}$-versions” of Eq. (3), which give different results for non-zero complex phases. We restricted ourselves to a version of our renormalization scheme which is valid for $|M_1| < |M_2|, |\mu |$ and $M_2 \ne \mu$ [where $M_1$ and $M_2$ denote the soft SUSY-breaking parameter of the $U(1)$ and $\mathrm{SU}(2)$ gauginos, and $\mu$ is the Higgs mixing parameter] to simplify the analysis, even though we are able to switch to other parameter regions; see the discussion in Refs. [63–65] (see also Ref. [66]).

Higher-order contributions to MSSM Higgs boson decays to charginos and neutralinos have been evaluated in various analyses over the last decade. In Ref. [67] the leading Yukawa corrections to $A/H \rightarrow \tilde{\chi }_{2}^0\tilde{\chi }_{2}^0, \tilde{\chi }_{1}^+\tilde{\chi }_{1}^-$ in the rMSSM have been evaluated, employing an on-shell (OS) scheme (referring to Ref. [68], but without providing further details). Next, in Ref. [69] the full one-loop corrections to $A/H \rightarrow \tilde{\chi }_{c^{}}^+\tilde{\chi }_{c^\prime }^-$ ($c,c^\prime = 1,2$) have been presented in the rMSSM (again without details as regards the OS-like scheme). An effective Lagrangian approach for heavy neutral Higgs boson decays in the rMSSM was published in Refs. [70, 71]. The full one-loop corrections to all heavy Higgs decays to charginos and neutralinos in the rMSSM in the ${\overline{\mathrm {DR}}}$ scheme were published in the code HFOLD [56]. In Refs. [72, 73] the main two-body decays of $A/H$ have been studied in scenarios where the only SUSY particles at low energies are the neutralinos and/or the charginos. More recently also evaluations of Higgs boson decays to charginos and neutralinos in the cMSSM became available. In Ref. [74] the decays $h_i \rightarrow \tilde{\chi }_{c^{}}^+\tilde{\chi }_{c^\prime }^-$ ($i = 1,2,3;\, c,c^\prime = 1,2$) were presented, together with a short discussion of different renormalization schemes (see Sect. 2.2) and a brief analysis of the dependence on the phases of $\mu$, $M_1$, and the trilinear Higgs stop coupling, $A_t$. The decays $h_i \rightarrow \tilde{\chi }_{n^{}}^0\tilde{\chi }_{n^\prime }^0$ ($i = 1,2,3;\, n,n^\prime = 1,2,3,4$) were calculated in Refs. [75, 76], where the numerical analysis concentrated on $h_{2,3} \rightarrow \tilde{\chi }_{2}^0\tilde{\chi }_{2}^0$ and the dependence on the phase of $A_t$. The last two references come close to the calculations presented in this paper. Small differences in the renormalization in the chargino/neutralino sector exist (see Sect. 2.2; Ref. [64]), where we use consistently the scheme detailed in Ref. [62] for all two-body decays simultaneously. In our numerical analysis we focus on the one parameter with a possible complex phase entering at the tree level, $M_1$; see the discussion in Sect. 3. A short numerical comparison with the literature, in particular with Refs. [56, 74–76], will be given in Sect. 4.1.

In this paper we present a full one-loop calculation for all two-body decay channels of the Higgs bosons into charginos and neutralinos in the cMSSM, taking into account soft and hard QED radiation. In Sect. 2 we briefly review the relevant sectors of the cMSSM. Details as regards the calculation can be found in Sect. 3, and the numerical results for all decay channels are presented in Sect. 4 (including comments on comparisons with the results from other groups). The conclusions can be found in Sect. 5. There are plans to implement the evaluation of the branching ratios of the heavy Higgs bosons into the Fortran code FeynHiggs [39–44], together with an automated choice of the renormalization scheme valid for the full cMSSM parameter space.

2 The complex MSSM

The channels (1)–(3) are calculated at the one-loop level, including soft and hard QED radiation. This requires the simultaneous renormalization of several sectors of the cMSSM: the Higgs and gauge boson sector as well as the chargino/neutralino sector. In the following subsections we very briefly review these sectors and their renormalization.

2.1 The Higgs and gauge boson sector

The Higgs and gauge boson sector follow strictly Ref. [62] and references therein (see especially Ref. [39]). This defines in particular the counterterm $\delta \tan \beta \equiv \delta t_\beta$, as well as the counterterms for the $Z$ boson mass, $\delta M_Z^2$, and for the sine of the weak mixing angle, $\delta s_{\mathrm {w}}$ (with $s_{\mathrm {w}}= \sqrt{1 - c_{\mathrm {w}}^2} = \sqrt{1 - M_W^2/M_Z^2}$, where $M_W$ denotes the $W$ boson mass).

2.2 The chargino/neutralino sector

The chargino/neutralino sector is also described in detail in Ref. [62] and references therein; see in particular Refs. [63–65]. In this paper we use the so-called “CCN” scheme, i.e. OS conditions for two charginos and one neutralino, which we choose to be the lightest one. Renormalizing the two charged states OS, i.e. ensuring that they have the same mass at the tree and at the loop level is (in general) crucial for the cancellation of the IR divergencies. In the notation of Ref. [62] we used:

$$\begin{aligned} \mathtt {\$InoScheme = CCN[1]}&\quad \text {fixed CCN scheme with on-}\\&\text {shell} \tilde{\chi }_{1}^0. \end{aligned}$$

This defines in particular the counterterm $\delta \mu$, where $\mu$ denotes the Higgs mixing parameter. This scheme yields numerically stable results for $|M_1| < |M_2|, |\mu |$ and $M_2 \ne \mu$, i.e. the lightest neutralino is bino-like and defines the counterterm for $M_1$ [63–66]. In the numerical analysis this mass pattern holds. Switching to a different mass pattern, e.g. with $|M_2| < |M_1|$ and/or $M_2 \sim \mu$ requires one to switch to a different renormalization scheme [62, 66]. While these schemes are implemented into the FeynArts/FormCalc framework [62], so far no automated choice of the renormalization scheme has been devised. For simplicity we stick to the CCN[1] scheme with a matching choice of SUSY parameters; see Sect. 4.2.

Since both chargino masses $m_{\tilde{\chi }_{1,2}^\pm }$ and the lightest neutralino mass $m_{\tilde{\chi }_{1}^0}$ have been chosen as independent parameters, the one-loop masses of the heavier neutralinos $\tilde{\chi }_{n}^0$ ($n$ = 2,3,4) are obtained from the tree-level ones via the shifts [75, 76]

$$\begin{aligned}&\Delta m_{\tilde{\chi }_{n}^0} = -\mathop {\mathrm {Re}}\left\{ m_{\tilde{\chi }_{n}^0} \left( \Sigma _{\tilde{\chi }_{n}^0}^L\left( m_{\tilde{\chi }_{n}^0}^2\right) \right. \right. \nonumber \\&\quad \left. \left. + \frac{1}{2} \left[ \delta \mathbf {Z}_{\tilde{\chi }_{}^0}^L + \delta \breve{\mathbf {Z}}_{\tilde{\chi }_{}^0}^L + \delta \mathbf {Z}_{\tilde{\chi }_{}^0}^R + \delta \breve{\mathbf {Z}}_{\tilde{\chi }_{}^0}^R \right] _{nn} \right) \right. \nonumber \\&\quad +\left. \Sigma _{\tilde{\chi }_{n}^0}^{SL}\left( m_{\tilde{\chi }_{n}^0}^2\right) - m_{\tilde{\chi }_{n}^0} \left[ \delta \mathbf {Z}_{\tilde{\chi }_{}^0}^L + \delta \breve{\mathbf {Z}}_{\tilde{\chi }_{}^0}^L \right] _{nn} - \left[ \delta \mathbf {M}_{\tilde{\chi }_{}^0} \right] _{nn} \right\} , \end{aligned}$$

(4)

where the renormalization constants $\delta \mathbf {Z}_{}$ and $\delta \breve{\mathbf {Z}}_{}$ can be found in Ref. [62]. For all externally appearing neutralino masses we use the (shifted) “on-shell” masses:

$$\begin{aligned} m_{\tilde{\chi }_{n}^0}^\mathrm {os}&= m_{\tilde{\chi }_{n}^0} + \Delta m_{\tilde{\chi }_{n}^0}. \end{aligned}$$

(5)

In order to yield UV-finite results we use the tree-level values $m_{\tilde{\chi }_{n}^0}$ for all internally appearing neutralino masses in loop calculations.

2.3 The fermion/sfermion sector

To be in accordance with Ref. [58], we use shifted (s)fermion masses in the loop corrections. As requirement for these shifts one needs the renormalization of the fermion/sfermion sector:

• The renormalization of the fermion sector is described in detail in Ref. [62] and references therein. For simplification we use the ${\overline{\mathrm {DR}}}$ renormalization for all three generations of down-type quarks and leptons, again in the notation of Ref. [62]:

  $$\begin{aligned}&\mathtt {UVMf1[4,\,\_] = UVDivergentPart}\\&\quad {\overline{\mathrm {DR}}}\ \text { renormalization for } m_d, m_s, m_b \\&\mathtt {UVMf1[2,\,\_] = UVDivergentPart}\\&\quad {\overline{\mathrm {DR}}}\text { renormalization for } m_e, m_\mu , m_\tau \end{aligned}$$

• The renormalization of the sfermion sector differs slightly from the one described in Ref. [62]. For the squark sector we follow Refs. [59–61] (which agrees with the renormalization scheme used in Refs. [63, 64, 77, 78]) and the slepton sector can be found in Ref. [58]. Concerning our notation we denote by $M_{\tilde{Q}_g, \tilde{L}_g, \tilde{U}_g, \tilde{D}_g, \tilde{E}_g}$ the “diagonal” soft SUSY-breaking parameters for the $\mathrm{SU}(2)$ squark, slepton doublet, the u-, d-type squark singlet, and the e-type slepton singlet, respectively, where $g$ is the generation index. Furthermore we use $A_{\mathrm {u}_g,\mathrm {d}_g,\mathrm {e}_g}$ for the trilinear Higgs-scalar u-, d-, e-type fermion couplings, respectively.

3 Calculation of loop diagrams

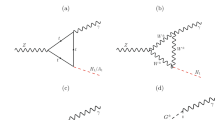
In this section we give some details as regards the calculation of the higher-order corrections to the partial decay widths of Higgs bosons. Sample diagrams for the decays $h_i \rightarrow \tilde{\chi }_{c}^- \tilde{\chi }_{c^\prime }^+$ ($i = 1,2,3;\, c,c^\prime = 1,2$), $h_i \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{n^\prime }^0$ ($i = 1,2,3;\, n,n^\prime = 1,2,3,4$) and $H^+ \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{c}^+$ ($n = 1,2,3,4;\, c = 1,2$) are shown in Figs. 1, 2, and 3, respectively. Not shown are the diagrams for real (hard and soft) photon radiation. They are obtained from the corresponding tree-level diagrams by attaching a photon to the electrically charged particles. The internal generically depicted particles in Figs. 1, 2, and 3 are labeled as follows: $F$ can be a SM fermion $f$, chargino $\tilde{\chi }_{c}^\pm$, neutralino $\tilde{\chi }_{n}^0$; $S$ can be a sfermion ${\tilde{f}}_s$ or a Higgs (Goldstone) boson $h_i$ $(G)$; $V$ can be a photon $\gamma$ or a massive SM gauge boson, $Z$ or $W^\pm$. For internally appearing Higgs bosons no higher-order corrections to their masses or couplings are taken into account; these corrections would correspond to effects beyond one-loop order.¹ For external Higgs bosons, as discussed in Ref. [39], the appropriate $\hat{Z}$ factors are applied and OS masses (including higher-order corrections) are used [39], obtained with FeynHiggs [39–44].

Fig. 1

Generic Feynman diagrams for the decay $h_i \rightarrow \tilde{\chi }_{c}^- \tilde{\chi }_{c^\prime }^+$ ($i = 1,2,3;\, c,c^\prime = 1,2$). $F$ can be a SM fermion, chargino, neutralino; $S$ can be a sfermion or a Higgs/Goldstone boson; $V$ can be a $\gamma$, $Z$, $W^\pm$. Not shown are the diagrams with a $h_i$–$Z$ or $h_i$–$G$ transition contribution on the external Higgs boson leg

Fig. 2

Generic Feynman diagrams for the decay $h_i \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{n^\prime }^0$ ($i = 1,2,3;\, n,n^\prime =1,2,3,4$). $F$ can be a SM fermion, chargino, neutralino; $S$ can be a sfermion or a Higgs/Goldstone boson; $V$ can be a $Z$ or $W^\pm$. Not shown are the diagrams with a $h_i$–$Z$ or $h_i$–$G$ transition contribution on the external Higgs boson leg

Fig. 3

Generic Feynman diagrams for the decay $H^+ \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{c}^+$ ($n = 1,2,3,4;\, c = 1,2$). (It should be noted that all arrows are inverted in the case of a $H^-$ decay.) $F$ can be a SM fermion, chargino, neutralino; $S$ can be a sfermion or a Higgs/Goldstone boson; $V$ can be a $\gamma$, $Z$, $W^\pm$. Not shown are the diagrams with a $H^\pm$–$W^\pm$ or $H^\pm$–$G^\pm$ transition contribution on the external Higgs boson leg

Also not shown are the diagrams with a Higgs boson-gauge/Goldstone self-energy contribution on the external Higgs boson leg. They appear in the decay $h_i \rightarrow \tilde{\chi }_{c}^- \tilde{\chi }_{c^\prime }^+$, Fig. 1, and $h_i \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{n^\prime }^0$, Fig. 2, with a $h_i$–$Z/G$ transition and in the decay $H^\pm \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{c}^\pm$, Fig. 3, with a $H^\pm$–$W^\pm$/$G^\pm$ transition.²

Furthermore, in general, in Figs. 1, 2, and 3 we have omitted diagrams with self-energy type corrections of external (on-shell) particles. While the contributions from the real parts of the loop functions are taken into account via the renormalization constants defined by OS renormalization conditions, the contributions coming from the imaginary part of the loop functions can result in an additional (real) correction if multiplied by complex parameters. In the analytical and numerical evaluation, these diagrams have been taken into account via the prescription described in Ref. [62].

Within our one-loop calculation we neglect finite width effects that can help to cure threshold singularities. Consequently, in the close vicinity of those thresholds our calculation does not give a reliable result. Switching to a complex mass scheme [79] would be another possibility to cure this problem, but its application is beyond the scope of our paper.

The diagrams and corresponding amplitudes have been obtained with FeynArts [80–82]. The model file, including the MSSM counterterms, is largely based on Ref. [62], however, adjusted to match exactly the renormalization prescription described in Sect. 2. The further evaluation has been performed with FormCalc and LoopTools [83].

3.1 Ultraviolet divergences

As the regularization scheme for the UV divergences we have used constrained differential renormalization [84], which has been shown to be equivalent to dimensional reduction [85, 86] at the one-loop level [83]. Thus the employed regularization scheme preserves SUSY [87, 88] and guarantees that the SUSY relations are kept intact, e.g. that the gauge couplings of the SM vertices and the Yukawa couplings of the corresponding SUSY vertices also coincide to one-loop order in the SUSY limit. Therefore, no additional shifts, which might occur when using a different regularization scheme, arise. All UV divergences cancel in the final result.

3.2 Infrared divergences

The IR divergences from diagrams with an internal photon have to cancel with the ones from the corresponding real soft radiation. We have included the soft and hard photon contribution via analytical formulas which are based on the bremsstrahlung integrals given in Appendix D of Ref. [68].³ The IR divergences arising from the diagrams involving a photon are regularized by introducing a photon mass parameter, $\lambda$. All IR divergences, i.e. all divergences in the limit $\lambda \rightarrow 0$, cancel once virtual and real photon radiation for one decay channel are added.

3.3 Tree-level formulas

For completeness we show here also the formulas that have been used to calculate the tree-level decay widths:

$$\begin{aligned}&\Gamma ^\mathrm{tree}(H^\pm \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{c}^\pm ) \nonumber \\&\quad = \Bigg [ \left( |C(H^\pm , \tilde{\chi }_{n}^0, \tilde{\chi }_{c}^\pm )_L|^2+ |C(H^\pm , \tilde{\chi }_{n}^0, \tilde{\chi }_{c}^\pm )_R|^2 \right) \nonumber \\&\quad \qquad (M_{H^{\pm }}^2 - m_{\tilde{\chi }_{n}^0}^2 - m_{\tilde{\chi }_{c}^\pm }^2) \nonumber \\&\quad \quad -\! 4\, \mathop {\mathrm {Re}}\left\{ C(H^\pm , \tilde{\chi }_{n}^0, \tilde{\chi }_{c}^\pm )_L^*\, C(H^\pm , \tilde{\chi }_{n}^0, \tilde{\chi }_{c}^\pm )_R\! \right\} \,\! m_{\tilde{\chi }_{n}^0}\, m_{\tilde{\chi }_{c}^\pm } \!\Bigg ] \nonumber \\&\quad \quad \times \frac{\lambda ^{1/2}(M_{H^{\pm }}^2,m_{\tilde{\chi }_{n}^0}^2,m_{\tilde{\chi }_{c}^\pm }^2)}{16\, \pi \, M_{H^{\pm }}^3} \quad (c = 1,2;\, n = 1,2,3,4), \end{aligned}$$

(6)

$$\begin{aligned}&\Gamma ^\mathrm{tree}(h_i \rightarrow \tilde{\chi }_{c}^- \tilde{\chi }_{c^\prime }^+) \nonumber \\&\quad = \Bigg [ \left( |C(h_i, \tilde{\chi }_{c^{}}^-, \tilde{\chi }_{c^\prime }^+)_L|^2 + |C(h_i, \tilde{\chi }_{c^{}}^-, \tilde{\chi }_{c^\prime }^+)_R|^2 \right) \nonumber \\&\quad \qquad (m_{h_{i}}^2 - m_{\tilde{\chi }_{c^{}}^-}^2 - m_{\tilde{\chi }_{c^\prime }^+}^2) \nonumber \\&\quad \quad - 4\, \mathop {\mathrm {Re}}\left\{ C(h_i, \tilde{\chi }_{c^{}}^-, \tilde{\chi }_{c^\prime }^+)_L^*\, C(h_i, \tilde{\chi }_{c^{}}^-, \tilde{\chi }_{c^\prime }^+)_R \right\} \, m_{\tilde{\chi }_{c^{}}^-}\, m_{\tilde{\chi }_{c^\prime }^+} \Bigg ] \nonumber \\&\quad \quad \times \frac{\lambda ^{1/2}(m_{h_{i}}^2,m_{\tilde{\chi }_{c^{}}^-}^2,m_{\tilde{\chi }_{c^\prime }^+}^2)}{16\, \pi \, m_{h_{i}}^3} \quad (i = 1,2,3;\, c,c^\prime = 1,2), \end{aligned}$$

(7)

$$\begin{aligned}&\Gamma ^\mathrm{tree}(h_i \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{n^\prime }^0) \nonumber \\&\quad = \Bigg [ \left( |C(h_i, \tilde{\chi }_{n}^0, \tilde{\chi }_{n^\prime }^0)_L|^2 + |C(h_i, \tilde{\chi }_{n}^0, \tilde{\chi }_{n^\prime }^0)_R|^2 \right) \nonumber \\&\quad \qquad (m_{h_{i}}^2 - m_{\tilde{\chi }_{n^{}}^0}^2 - m_{\tilde{\chi }_{n^\prime }^0}^2) \nonumber \\&\quad \quad - 4\, \mathop {\mathrm {Re}}\left\{ C(h_i, \tilde{\chi }_{n^{}}^0, \tilde{\chi }_{n^\prime }^0)_L^*\, C(h_i, \tilde{\chi }_{n^{}}^0, \tilde{\chi }_{n^\prime }^0)_R \right\} \, m_{\tilde{\chi }_{n^{}}^0}\, m_{\tilde{\chi }_{n^\prime }^0} \Bigg ] \nonumber \\&\quad \quad \times \frac{\lambda ^{1/2}(m_{h_{i}}^2,m_{\tilde{\chi }_{n^{}}^0}^2,m_{\tilde{\chi }_{n^\prime }^0}^2)}{16\, \pi \, m_{h_{i}}^3} \quad (i \!=\! 1,2,3;\, n,n^\prime \!=\! 1,2,3,4), \end{aligned}$$

(8)

where $\lambda (x,y,z) = (x - y - z)^2 - 4yz$. The couplings $C(a, b, c)$ can be found in the FeynArts model files; see Ref. [89]. $C(a, b, c)_{L,R}$ denote the part of the coupling which is proportional to $({\small 1}\!\!1\mp \gamma _5)/2$. For the interpretation of the results in the numerical analysis below the following should be kept in mind. In Eqs. (7) and (8) the couplings of the Higgs to charginos/neutralinos result in a relative plus (minus) sign between the two terms (in the first and second line of each equation, respectively) for $h_i$ being a ${\mathcal CP}$-odd (${\mathcal CP}$-even) Higgs, leading to an enhancement (suppression) of the decay width. In the case of equal final state masses ($c = c^\prime$ or $n = n^\prime$) one finds in FeynArts convention⁴ $C(h_i, \tilde{\chi }_{}, \tilde{\chi }_{})_L = -C(h_i, \tilde{\chi }_{}, \tilde{\chi }_{})^*_R =: C(h_i, \tilde{\chi }_{}, \tilde{\chi }_{})$, and the general structure of the tree-level decay width simplifies for real parameters to

$$\begin{aligned}&\Gamma ^\mathrm{tree}(h_i \rightarrow \tilde{\chi }_{} \tilde{\chi }_{})\nonumber \\&\quad =\! \frac{|C(h_i, \tilde{\chi }_{}, \tilde{\chi }_{})|^2}{8\, \pi } \left[ m_{h_{i}}^2 \!-\! 4\, m_{\tilde{\chi }_{}}^2 \right] ^{(1/2)} \quad \text {for } h_{i}\,\, {\mathcal CP}\hbox {-odd}, \end{aligned}$$

(9)

$$\begin{aligned}&\Gamma ^\mathrm{tree}(h_i \rightarrow \tilde{\chi }_{} \tilde{\chi }_{})\nonumber \\&\quad = \!\frac{|C(h_i, \tilde{\chi }_{}, \tilde{\chi }_{})|^2}{8\, \pi \, m_{h_{i}}^2} \left[ m_{h_{i}}^2 \!-\! 4\, m_{\tilde{\chi }_{}}^2 \right] ^{(3/2)} \quad \text {for } h_{i}\,\, {\mathcal CP}\hbox {-even}. \end{aligned}$$

(10)

The latter decay width exhibits a $p$-wave suppression.

4 Numerical analysis

In this section we present the comparisons with results from other groups and our numerical analysis of the light and heavy Higgs boson decay channels into charginos and neutralinos in the cMSSM. In the various figures below we show the partial decay widths and their relative correction at the tree level (“tree”) and at the one-loop level (“full”).

4.1 Comparisons

We performed exhaustive comparisons with results from other groups for Higgs boson decays into charginos and neutralinos. Most of these comparisons were restricted to the MSSM with real parameters. The level of agreement of such comparisons depends on the correct transformation from our renormalization scheme into the schemes used in the respective literature. In view of the non-trivial conversion and the large number of comparisons this is beyond the scope of our paper. Nevertheless this subsection will give an impression that our scheme is reliable and compatible to the wide range of other schemes used in the literature.

• A comparison with Ref. [67] (in the rMSSM) gave an overall qualitative agreement for the decays $H/A \rightarrow \tilde{\chi }_{1}^+ \tilde{\chi }_{1}^-$, as was to be expected, because that work took into account only the leading Yukawa corrections and used a different renormalization scheme. On the other hand, we omit a comparison with the results for $H/A \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{2}^0$ of Ref. [67], because in their setup neutralino masses were used as input parameters, which is rather difficult to adapt to our numerical analysis setup.

• For the comparison with Ref. [69] we calculated the decays $A/H \rightarrow \tilde{\chi }_{1}^+ \tilde{\chi }_{1}^-$ at $\mathcal{O}(\alpha (M_Z))$, using their input parameters as far as possible. We found good (qualitative) agreement with Ref. [69] (where the calculation was restricted to the rMSSM). We successfully reproduced their Figs. 2, 4, 5 and 6, where only a small difference remains due to the different renormalization schemes; see also Table 1 with differences below 5 %.

• We performed a numerical comparison with Refs. [70, 71] for the decay $H/A \rightarrow \tilde{\chi }_{1}^+ \tilde{\chi }_{1}^-$ at $\mathcal{O}(\alpha (M_Z))$ (in the rMSSM); see Table 1, where the columns for Refs. [69–71] where taken over from Table 1 of the first article in Refs. [70, 71]. Their setup differs from ours in the renormalization of the chargino/neutralino sector, leading to different loop corrections. Furthermore they used an “effective one-loop Lagrangian”. Nevertheless, using their input parameters as far as possible, we found differences below the 10 % level.

• A numerical comparison with the program HFOLD Ref. [56] at the benchmark point SPS1a‘ (proposed in the SPA project [90]) can be found in Table 2. Since our results are not yet included in FeynHiggs we do not have an interface to the SLHA standard and are confined to the one point that is given in more detail in Ref. [56]. In Table 2 we show the full one-loop results of HFOLD, using ${\overline{\mathrm {DR}}}$ masses for the internal and external particles, corresponding to the full ${\overline{\mathrm {DR}}}$ renormalization used in the code (where the renormalization scale was set to $1\, \mathrm {TeV}$ [90]). Our results, labeled FeynTools, are evaluated using our renormalization scheme, but inserting the HFOLD ${\overline{\mathrm {DR}}}$ masses. In the tree-level results we find more than ten digits agreement and in the full results we find agreement of 3–15 % (7 % on average).⁵ HFOLD also offers to switch to (the recommended) OS masses for the external particles. In this case, we are including in our calculation $m_{\tilde{\chi }_{2}^0}^\mathrm {os}$ as described in Sect. 2.2, Eq. (5), but using the same OS Higgs boson masses as in HFOLD. With it the agreement between the two calculations is 11 % on average (5–22 %).

• Decays of $h_{2,3}$ to charginos in the cMSSM at the full one-loop level have been numerically compared with Ref. [74] using their latest FeynArts model file implementation. We found overall agreement better than 1 % in the loop corrections for real and complex parameters.⁶

• $h_{2,3}$ boson decays into $\tilde{\chi }_{2}^0 \tilde{\chi }_{2}^0$ in the cMSSM have been analyzed in Refs. [75, 76]. Again we had to use here the latest FeynArts model file implementation of Ref. [74] (which is based mainly on code from Refs. [75, 76]) for the same reasons as described in the previous item. In comparison with that model file [74] we found overall agreement better than 2 % in the loop corrections for real and complex parameters.

Fig. 4

$\Gamma (H^\pm \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{1}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S3 (see Table 3)

Fig. 5

$\Gamma (H^\pm \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{2}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S3 (see Table 3)

Fig. 6

$\Gamma (H^\pm \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{1}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S3 (see Table 3)

Table 1 Comparison of the one-loop corrected partial decay widths (in GeV) with Refs. [70, 71]

Table 2 Comparison of the one-loop corrected partial decay widths (in $10^{-1}\, \mathrm {GeV}$) with HFOLD

Table 3 MSSM parameters for the initial numerical investigation; all parameters (except of $t_\beta$) are in GeV (calculated masses are rounded to 1 MeV). In our analysis $M_{\tilde{Q}_3}$, $M_{\tilde{U}_3}$, $M_{\tilde{D}_3}$, $M_{\tilde{L}_3}$ and $M_{\tilde{E}_3}$ are chosen such that the values of $m_{\tilde{t}_{1}}$, $m_{\tilde{t}_{2}}$, $m_{\tilde{b}_{2}}$, $m_{\tilde{\nu }_{\tau }}$ and $m_{\tilde{\tau }_{2}}$ are realized. For the sfermion sector the shifts in $M_{\tilde{Q}, \tilde{D}}({\tilde{\mathrm{d}}}_g)$ and $M_{\tilde{L}, \tilde{E}}({\tilde{\mathrm{e}}}_g)$ as defined in Ref. [58] are taken into account. The values for the trilinear sfermion Higgs couplings, $A_{\mathrm {u}_g,\mathrm {d}_g,\mathrm {e}_g}$ ($g = 1,2,3$; identical for all $g$) are chosen such that charge- and/or color-breaking minima are avoided [93–99]. It should be noted that for the first and second generation of sfermions we chose instead $M_{\tilde{L}, \tilde{E}} = 1500\, \mathrm {GeV}$ and $M_{\tilde{Q}, \tilde{U}, \tilde{D}} = 2000\, \mathrm {GeV}$. For the neutralino sector the shifts in Eq. (4) are taken into account

4.2 Parameter settings

The renormalization scale $\mu _R$ has been set to the mass of the decaying Higgs boson. The SM parameters are chosen as follows; see also [92]:

• Fermion masses (on-shell masses, if not indicated differently):

  $$\begin{aligned} m_e&= 0.510998928\, \mathrm {MeV}, \quad m_{\nu _e} = 0\, \mathrm {MeV}, \nonumber \\ m_\mu&= 105.65837515\, \mathrm {MeV}, \quad m_{\nu _{\mu }} = 0\, \mathrm {MeV}, \nonumber \\ m_\tau&= 1776.82\, \mathrm {MeV}, \quad m_{\nu _{\tau }} = 0\, \mathrm {MeV}, \nonumber \\ m_u&= 68.7\, \mathrm {MeV}, \quad m_d = 68.7\, \mathrm {MeV}, \nonumber \\ m_c&= 1.275\, \mathrm {GeV}, \quad m_s = 95.0\, \mathrm {MeV}, \nonumber \\ m_t&= 173.21\, \mathrm {GeV}, \quad m_b = 4.18\, \mathrm {GeV}. \end{aligned}$$

  (11)

  According to Ref. [92], $m_s$ is an estimate of a so-called “current quark mass” in the $\overline{\mathrm {MS}}$ scheme at the scale $\mu \approx 2\, \mathrm {GeV}$. $m_c \equiv m_c(m_c)$ and $m_b \equiv m_b(m_b)$ are the “running” masses in the $\overline{\mathrm {MS}}$ scheme.⁷ $m_u$ and $m_d$ are effective parameters, calculated through the hadronic contributions to

  $$\begin{aligned}&\Delta \alpha _{\text {had}}^{(5)}(M_Z)\nonumber \\&= \frac{\alpha }{\pi }\sum _{f = u,c,d,s,b} Q_f^2 \left( \ln \frac{M_Z^2}{m_f^2} - \frac{5}{3}\right) \sim 0.027723. \end{aligned}$$

  (12)

• Gauge boson masses:

  $$\begin{aligned} M_Z = 91.1876\, \mathrm {GeV}, \quad M_W = 80.385\, \mathrm {GeV}. \end{aligned}$$

  (13)

• Coupling constant:

  $$\begin{aligned} \alpha (0) = 1/137.0359895. \end{aligned}$$

  (14)

The Higgs sector quantities (masses, mixings, etc.) have been evaluated using FeynHiggs (version 2.10.2) [39–44].

We emphasize again that the analytical calculation has been done for all decays into charginos/neutralinos. Results are shown for some representative numerical examples. The parameters are chosen according to the scenarios, SX $(X = 1,2,\ldots ,5)$, shown in Table 3, unless otherwise noted. The scenarios are defined such that a maximum number of decay modes are open simultaneously to permit an analysis of all channels, i.e. not picking specific parameters for each decay. For the same reason we do not demand that the lightest Higgs boson has a mass around $\sim$ $125\, \mathrm {GeV}$, although for most of the parameter space this is given. For the light Higgs we will show the variation with $M_{H^{\pm }}$, $|\mu |$, $M_1$, and $\varphi _{M_1}$ (where the last symbol denotes the phase of the gaugino mass parameter $M_1$), whereas for the heavy Higgs bosons we will analyze the variation of $M_{H^{\pm }}$ and $\varphi _{M_1}$.

The numerical results shown in the next subsections are of course dependent on the choice of the SUSY parameters. Nevertheless, they give an idea of the relevance of the full one-loop corrections. Channels (and their respective one-loop corrections) that may look unobservable due to the smallness of their decay width in the plots shown below could become important if other channels are kinematically forbidden.

4.3 Full one-loop results for varying $M_{H^{\pm }}$, $M_1$, and $\varphi _{M_1}$

The results shown in this and the following subsections consist of “tree”, which denotes the tree-level value and of “full”, which is the partial decay width including all one-loop corrections as described in Sect. 3. We restrict ourselves to the analysis of the decay widths themselves, since the one-loop effects on the branching ratios are strongly parameter dependent, as discussed in the previous subsection.

When performing an analysis involving complex parameters it should be noted that the results for physical observables are affected only by certain combinations of the complex phases of the parameters $\mu$, the trilinear couplings $A_f$, and the gaugino mass parameters $M_{1,2,3}$ [100, 101]. It is possible, for instance, to rotate the phase $\varphi _{M_2}$ away. Experimental constraints on the (combinations of) complex phases arise, in particular, from their contributions to electric dipole moments of the electron and the neutron (see Refs. [102–104] and references therein), of the deuteron [105] and of heavy quarks [106, 107]. While SM contributions enter only at the three-loop level, due to its complex phases the MSSM can contribute already at one-loop order. Large phases in the first two generations of sfermions can only be accommodated if these generations are assumed to be very heavy [108, 109] or large cancellations occur [110–112]; see, however, the discussion in Ref. [113]. A review can be found in Ref. [114]. Accordingly (using the convention that $\varphi _{M_2}= 0$, as done in this paper), in particular, the phase $\varphi _{\mu }$ is tightly constrained [115], while the bounds on the phases of the third generation trilinear couplings are much weaker. Setting $\varphi _{\mu }= 0$ and $\varphi _{A_f} = 0$ leaves us with $\varphi _{M_1}$ as the only complex valued parameter.

Since now the complex gaugino mass parameter $M_1$ can appear in the couplings, contributions from absorptive parts of self-energy type corrections on external legs can arise. The corresponding formulas for an inclusion of these absorptive contributions via finite wave function correction factors can be found in Refs. [61, 62].

We begin the numerical analysis with partial decay widths of $H^\pm$ evaluated as a function of $M_{H^{\pm }}$, starting at $M_{H^{\pm }}= 600\, \mathrm {GeV}$ up to $M_{H^{\pm }}= 1.6\, \mathrm {TeV}$, which roughly coincides with the reach of the LHC for high-luminosity running as well as an $e^+e^-$ collider with a center-of-mass energy up to $\sqrt{s} \sim 3\, \mathrm {TeV}$ [20, 21]. Then we turn to the $h_i$ ($i = 1,2,3$) decays. Finally, it should be noted that we expect from the tree-level equations (6)–(8) that the decay widths increase (roughly) linearly with the corresponding Higgs boson masses.

4.3.1 $H^\pm$ decays into charginos/neutralinos

In Figs. 4, 5, 6, 7, 8, 9, 10, and 11 we show the results for the processes $H^\pm \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{c}^\pm$ ($n = 1,2,3,4;\, c = 1,2$) as a function of $M_{H^{\pm }}$ and as a function of the relevant complex phase $\varphi _{M_1}$. These are of particular interest for LHC analyses [116, 117] (as emphasized in Sect. 1). The various visible (or hardly visible) dips/thresholds occurring for different values of $M_{H^{\pm }}$ in the plots are summarized in Table 4, labeled TC1–TC7.

Fig. 7

$\Gamma (H^\pm \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{2}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 8

$\Gamma (H^\pm \rightarrow \tilde{\chi }_{3}^0 \tilde{\chi }_{1}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S3 (see Table 3)

Fig. 9

$\Gamma (H^\pm \rightarrow \tilde{\chi }_{3}^0 \tilde{\chi }_{2}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 10

$\Gamma (H^\pm \rightarrow \tilde{\chi }_{4}^0 \tilde{\chi }_{1}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 11

$\Gamma (H^\pm \rightarrow \tilde{\chi }_{4}^0 \tilde{\chi }_{2}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S5 (see Table 3)

Table 4 Thresholds in charged Higgs boson decays

We start with the decay $H^\pm \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{1}^\pm$. In the left plot of Fig. 4 the first (small) dip is the threshold TC1, see Table 4. The second (large) dip is an effect due to the threshold TC2. The third “apparently single” dip is in reality two dips coming from the thresholds TC3 and TC4. The fourth (small) dip is the threshold TC5 and the last (large) one is the threshold TC6. The size of the corrections of the partial decay widths can be especially large very close to the production threshold⁸ from which on the considered decay mode is kinematically possible. Away from this production threshold relative corrections of $\sim$ $+10\,\%$ are found.

In the right plot of Fig. 4 we show the results for the complex phase $\varphi _{M_1}$ varying for $M_{H^{\pm }}= 1000\, \mathrm {GeV}$. The full corrections are up to $\sim$ $+13\,\%$ at $\varphi _{M_1}= 180^\circ$. At $\varphi _{M_1}= 90^\circ$ the $H^+$ ($H^-$) full corrections reach $\sim$ $+12\,\%$ ($\sim$ $+10\,\%$). Clearly visible is the ${\mathcal CP}$-asymmetry for the decays of the $H^+$ and $H^-$, which can reach the level of several per-cent.

In Fig. 5 we show the results for $H^\pm \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{2}^\pm$. The tree-level decay width $\Gamma (H^\pm \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{2}^\pm )$ happens to be very small for the parameter set chosen; see Table 3. Because of this smallness, the relative size of the one-loop correction becomes larger than the tree-level result, and turn the decay width, $\propto |\mathcal{M}_{{\mathrm{tree}}}|^2 + 2\mathop {\mathrm {Re}}\{\mathcal{M}_{{\mathrm{tree}}}^*\, \mathcal{M}_{\text {1-loop}}^{}\}$, negative. Therefore, only in this case we added the two-loop contribution $|\mathcal{M}_{\text {1-loop}}|^2$ to the full one-loop result to obtain at least a positive decay width.⁹ In the left plot the first (large) spike is the threshold TC2; see Table 4 enhanced through the two-loop contribution $|\mathcal{M}_{\text {1-loop}}|^2$ (i.e. without the explicit two-loop correction the spike would be a “usual dip”). The second “apparently single spike” (hardly visible) is (again) in reality the two thresholds TC3 and TC4. The next (apparently single) “dip” is in reality two steps (anomalous thresholds; see p. 376 and Eqs. (5.1)–(5.6) in Ref. [118]) traced back to the $C$-functions $C_{0,1,2}(M_{H^{\pm }}^2,m_{\tilde{\chi }_{2}^\pm }^2,m_{\tilde{\chi }_{1}^0}^2,m_{\tilde{\chi }_{4}^0}^2,m_{\tilde{\chi }_{1}^\pm }^2,m_{h_{1}}^2)$ at $M_{H^{\pm }}\approx 1126\, \mathrm {GeV}$ and $C_{0,1,2}(M_{H^{\pm }}^2,m_{\tilde{\chi }_{2}^\pm }^2,m_{\tilde{\chi }_{1}^0}^2,m_{\tilde{\chi }_{2}^\pm }^2,m_{\tilde{\chi }_{2}^0}^2,M_W^2)$ at $M_{H^{\pm }}\approx 1129\, \mathrm {GeV}$.¹⁰ Not visible (in the plot) is a spike, which is the threshold TC5. The last spike is the threshold TC6. Relative corrections of $\sim$ $-90\,\%$ are found at $M_{H^{\pm }}= 1000\, \mathrm {GeV}$ (see Table 3), where it should be kept in mind that the tree level already happens to be very small and thus loop corrections can have a relatively large impact.

In the right plot of Fig. 5 the results are shown for S3 as a function of $\varphi _{M_1}$. At $\varphi _{M_1}= 180^\circ$ the full corrections reach $\sim$ $-55\,\%$, again related to the small tree-level result that happens to occur. At $\varphi _{M_1}= 90^\circ$ the $H^+$ ($H^-$) full corrections reach $\sim$ $-59\,\%$ ($\sim$ $-62\,\%$), showing a small ${\mathcal CP}$-asymmetry.

Next, in Fig. 6 the results for $H^\pm \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{1}^\pm$ are displayed. In the left plot the results are shown as a function of $M_{H^{\pm }}$. The four visible dips here are exactly the same as in Fig. 4 (described above), beginning at $M_{H^{\pm }}= 976\, \mathrm {GeV}$. Relative corrections of $\sim$ $+33\,\%$ ($\sim$ $+21\,\%$) are found at $M_{H^{\pm }}= 1000\, \mathrm {GeV}$ ($M_{H^{\pm }}= 1400\, \mathrm {GeV}$); see Table 3.

In the right plot the results are displayed as a function of $\varphi _{M_1}$ in S3, i.e. for $M_{H^{\pm }}= 1000\, \mathrm {GeV}$. One can see that the size of the tree level as well as the corrections to the partial decay width vary substantially with the complex phase $\varphi _{M_1}$. For all $\varphi _{M_1}$ the full corrections lie between $+29$ and $+70\,\%$.¹¹ At $\varphi _{M_1}= 90^\circ$ the $H^+$ ($H^-$) full one-loop corrections reach $\sim$ $+29\,\%$ ($\sim$ $+48\,\%$), i.e. the ${\mathcal CP}$-asymmetry is rather large with $\sim$ $\pm 19\,\%$.

The decay $H^\pm \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{2}^\pm$ is shown in Fig. 7. In the left plot the results are shown as a function of $M_{H^{\pm }}$. The first (hardly visible) dip is (again) the threshold TC5, see Table 4, and the second (large) one is the threshold TC6. The decay width turns out to be relatively large at $\mathcal{O}(1\, \mathrm {GeV})$. Relative corrections of $\sim$ $+6\,\%$ ($\sim$ $+4\,\%$) are found at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ ($M_{H^{\pm }}= 1400\, \mathrm {GeV}$); see Table 3.

In the right plot of Fig. 7 the results are displayed as a function of $\varphi _{M_1}$ in S4, i.e. for $M_{H^{\pm }}= 1200\, \mathrm {GeV}$. The full corrections at $\varphi _{M_1}= 180^\circ$ reach $\sim$ $+7\,\%$. On the other hand it can be seen that the variation with $\varphi _{M_1}$ and the ${\mathcal CP}$-asymmetries ($\sim$ $\pm 0.1\,\%$) are rather small.

Next, in Fig. 8 the results for $H^\pm \rightarrow \tilde{\chi }_{3}^0 \tilde{\chi }_{1}^\pm$ are displayed. In the left plot the results are shown as a function of $M_{H^{\pm }}$. Here the four visible dips are the same as in Fig. 4, beginning at $M_{H^{\pm }}= 976\, \mathrm {GeV}$. Relative corrections of $\sim$ $-18\,\%$ ($\sim$ $-10\,\%$) are found at $M_{H^{\pm }}= 1000\, \mathrm {GeV}$ ($M_{H^{\pm }}= 1400\, \mathrm {GeV}$); see Table 3.

In the right plot the results are displayed as a function of $\varphi _{M_1}$ in S3. One can see that again the tree-level results as well as the size of the corrections to the partial decay width vary substantially with the complex phase $\varphi _{M_1}$. The full corrections can reach $\sim$ $-24\,\%$ and the ${\mathcal CP}$-asymmetry is found to be small at the level of $\sim$ $\pm 2\,\%$.

In Fig. 9 we show the results for $H^\pm \rightarrow \tilde{\chi }_{3}^0 \tilde{\chi }_{2}^\pm$. In the left plot (with $M_{H^{\pm }}$ varying) the dip is (again) the threshold TC6; see Table 4. The decay width is found to be of the same order as for $H^\pm \rightarrow \tilde{\chi }_{2}^0\tilde{\chi }_{2}^\pm$. One-loop corrections of $\sim$ $+5\,\%$ ($\sim$ $+4\,\%$) are found at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ in S4 ($M_{H^{\pm }}= 1400\, \mathrm {GeV}$ in S5); see Table 3.

In the right plot of Fig. 9 the results are shown for S4 as a function of $\varphi _{M_1}$. At $\varphi _{M_1}= 180^\circ$ the full corrections reach $\sim$ $+5\,\%$. At $\varphi _{M_1}= 90^\circ$ the $H^+$ ($H^-$) full corrections reach $\sim$ $+6\,\%$ ($\sim$ $+5\,\%$), i.e. the ${\mathcal CP}$-asymmetries are at the level of $\sim$ $\pm 1\,\%$.

We finish the charged Higgs-boson analysis with the decays involving the heaviest neutralino in Figs. 10 and 11, showing the results for $\Gamma (H^\pm \rightarrow \tilde{\chi }_{4}^0\tilde{\chi }_{1}^\pm )$ and $\Gamma (H^\pm \rightarrow \tilde{\chi }_{4}^0\tilde{\chi }_{2}^\pm )$, respectively.

In the left plot of Fig. 10 the first dip (not visible in the plot) is the threshold TC4; see Table 4. The second (small) dip is (again) the threshold TC5 and the third (large) dip is the threshold TC6. The first step (not visible in the plot) at $M_{H^{\pm }}\approx 1136\, \mathrm {GeV}$ is the anomalous threshold of the $C$-functions $C_{0,1,2}(M_{H^{\pm }}^2,m_{\tilde{\chi }_{1}^\pm }^2,m_{\tilde{\chi }_{4}^0}^2,m_{\tilde{\chi }_{3}^0}^2,m_{\tilde{\chi }_{2}^\pm }^2,M_Z^2)$. The second anomalous threshold at $M_{H^{\pm }}\approx 1340\, \mathrm {GeV}$ is caused by $C_{0,1,2}(m_{\tilde{\chi }_{4}^0}^2,M_{H^{\pm }}^2,m_{\tilde{\chi }_{1}^\pm }^2,m_b^2,m_{\tilde{b}_{1}}^2,m_{\tilde{t}_{2}}^2)$. The last dip (also not visible) is the threshold TC7. The decay width is again found at $\mathcal{O}(1\, \mathrm {GeV})$ with relative corrections of $\sim$ $+6\,\%$ in S4 (see Table 3).

In the right plot of Fig. 10 we show the complex phase $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$. The full corrections are up to $\sim$ $+6\,\%$ at $\varphi _{M_1}= 180^\circ$. Here the asymmetries are extremely small and hardly visible.

Finally, we discuss the decay $H^\pm \rightarrow \tilde{\chi }_{4}^0\tilde{\chi }_{2}^\pm$ in Fig. 11. The overall size of this decay width (with real phases) is (accidentally) very small around $1 \times 10^{-3}\, \mathrm {GeV}$. Consequently, the loop corrections, can be larger than the tree-level result. In the left plot the results are shown as a function of $M_{H^{\pm }}$. The (small) dip is the threshold TC6; see Table 4. Relative corrections of $\sim$ $+56\,\%$ are found at $M_{H^{\pm }}= 1400\, \mathrm {GeV}$ (see Table 3).

In the right plot the results are displayed as a function of $\varphi _{M_1}$ in S5. One can see that the size of the corrections to the partial decay width vary substantially with the complex phase $\varphi _{M_1}$. For all $\varphi _{M_1}$ the full corrections deviate between $+40$ and $+146\,\%$. (The latter value is reached at $\varphi _{M_1}= 180^\circ$ where the tree is extremely small $\sim$ $1 \times 10^{-4}\, \mathrm {GeV}$.) At $\varphi _{M_1}= 90^\circ$ the $H^+$ ($H^-$) full one-loop corrections reach $\sim$ $+40\,\%$ ($\sim$ $+103\,\%$), i.e. the ${\mathcal CP}$-asymmetries are very large with $\sim$ $\pm 60\,\%$.

Overall, for the charged Higgs boson decays to a chargino/neutralino pair we observe, as expected, an increasing decay width $\propto M_{H^{\pm }}$.¹² The full one-loop corrections reach a level of $10\,\%$ for decay widths of $\mathcal{O}(1\, \mathrm {GeV})$. The variation with $\varphi _{M_1}$ is found largest for very small decay widths, but can reach the level of 10–50 % for widths at or below the $1\, \mathrm {GeV}$ level. The ${\mathcal CP}$-asymmetries exceed the level of a few percent only for very small decay widths.

4.3.2 $h_i$ decays into charginos and neutralinos

We now turn to the decay modes $h_i \rightarrow \tilde{\chi }_{c}^- \tilde{\chi }_{c^\prime }^+$ ($i = 2,3;\, c,c^\prime = 1,2$) and $h_i \rightarrow \tilde{\chi }_{n}^0 \tilde{\chi }_{n^\prime }^0$ ($i = 1,2,3;\, n,n^\prime = 1,2,3,4$). Results are shown in the Figs. 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, and 25.

Fig. 12

$\Gamma (h_i \rightarrow \tilde{\chi }_{1}^\mp \tilde{\chi }_{1}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 13

$\Gamma (h_i \rightarrow \tilde{\chi }_{2}^\mp \tilde{\chi }_{2}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S5 (see Table 3)

Fig. 14

$\Gamma (h_i \rightarrow \tilde{\chi }_{1}^\mp \tilde{\chi }_{2}^\pm )$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 15

$\Gamma (h_1 \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{1}^0)$. Tree-level and full one-loop corrected partial decay widths are shown with parameters chosen according to S1 (see Table 3) but here with $|M_1| = 50\, \mathrm {GeV}$. The upper left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The upper right plot shows the complex phase $\varphi _{M_1}$ varying. The lower left (right) plot shows $M_1$ ($|\mu |$) varying

Fig. 16

$\Gamma (h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{1}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S1 (see Table 3)

Fig. 17

$\Gamma (h_i \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{2}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 18

$\Gamma (h_i \rightarrow \tilde{\chi }_{3}^0 \tilde{\chi }_{3}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 19

$\Gamma (h_i \rightarrow \tilde{\chi }_{4}^0 \tilde{\chi }_{4}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S5 (see Table 3)

Fig. 20

$\Gamma (h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{2}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S2 (see Table 3)

Fig. 21

$\Gamma (h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{3}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S2 (see Table 3)

Fig. 22

$\Gamma (h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{4}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 23

$\Gamma (h_i \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{3}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 24

$\Gamma (h_i \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{4}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Fig. 25

$\Gamma (h_i \rightarrow \tilde{\chi }_{3}^0 \tilde{\chi }_{4}^0)$. Tree-level and full one-loop corrected partial decay widths are shown. The left plot shows the partial decay width with $M_{H^{\pm }}$ varying. The right plot shows the complex phase $\varphi _{M_1}$ varying with parameters chosen according to S4 (see Table 3)

Before discussing every figure in detail, it should be noted that there is a subtlety concerning the mixture of the $h_i$ bosons. Depending on the input parameters, the higher-order corrections to the three neutral Higgs boson masses can vary substantially. The mass ordering $m_{h_{1}} < m_{h_{2}} < m_{h_{3}}$ (as performed automatically by FeynHiggs), even in the case of real parameters, can yield a heavy ${\mathcal CP}$-even Higgs mass higher or lower than the (heavy) ${\mathcal CP}$-odd Higgs mass. Such a transition in the mass ordering (or “mass crossing”) is accompanied by an abrupt change in the Higgs mixing matrix $\hat{\mathbf {Z}}$.¹³ For our input parameters (see Table 3) there are two (possible) crossings. The first (called “MC1” below) appears at $M_{H^{\pm }}\approx 1006\, \mathrm {GeV}$. Before the crossing we find $h_2 \sim H$ ($h_3 \sim A$), whereas after the crossing it changes to $h_2 \sim A$ ($h_3 \sim H$). The second crossing (called “MC2”) is found at $M_{H^{\pm }}\approx 1532\, \mathrm {GeV}$, i.e. the changing of the mixture from $h_2 \sim A$ ($h_3 \sim H$) to $h_2 \sim H$ ($h_3 \sim A$). Very close to the mass crossings the $\hat{\mathbf {Z}}$ matrix can yield small numerical instabilities. As an example, for $1532\, \mathrm {GeV}\lesssim M_{H^{\pm }}\lesssim 1536\, \mathrm {GeV}$ the $\hat{\mathbf {Z}}$ matrix causes structures appearing similar to “usual” dips from thresholds (see also the discussion in Ref. [58]). All the dips/thresholds (some are hardly visible) appearing in the figures below are listed in Table 5, labeled as TN1 to TN13.

Table 5 Thresholds in neutral Higgs boson decays

4.3.3 $h_i$ decays into charginos

In this subsection we analyze the decays of the heavy neutral Higgs bosons into charginos. We start with the decay $h_i \rightarrow \tilde{\chi }_{1}^\mp \tilde{\chi }_{1}^\pm$ $(i = 2,3)$ as shown in Fig. 12. The left plot shows the results as a function of $M_{H^{\pm }}$, whereas in the right plot we present the decay widths as a function of $\varphi _{M_1}$ in S4. We show separately the results for the $h_2$ and $h_3$ decay widths. In the left plot of Fig. 12 the first “apparently single” dip in the $h_2$ decay (upper lines) is in reality coming from the thresholds TN6 and TN7; see Table 5. The second (large) dip is the threshold TN10. The last “apparently single” dip is in reality coming from the thresholds TN11 and TN12. The “step” (anomalous threshold) at $M_{H^{\pm }}\approx 1310\, \mathrm {GeV}$ could be traced back to the $C$-functions $C_{0,1,2}(m_{\tilde{\chi }_{1}^\pm }^2,m_{h_{2}}^2,m_{\tilde{\chi }_{1}^\pm }^2,m_b^2,m_{\tilde{t}_{s^{}}}^2,m_{\tilde{t}_{s^\prime }}^2)$ with $s^{}\ne s^\prime$. Away from the production threshold relative corrections of $\sim$ $-3\,\%$ are found in S4 (see Table 3) for the $h_2$ decay. The loop corrections increase with increasing $M_{H^{\pm }}$ and reach $\sim$ $-10\,\%$ in S5. In the case of the $h_3$ decay the dips are the same as for $h_2$ and the relative corrections are only $\sim$ $-2\,\%$ in S4 (see Table 3). The two mass crossings MC1 and MC2 are clearly visible at $M_{H^{\pm }}\approx 1006\, \mathrm {GeV}$ and $M_{H^{\pm }}\approx 1532\, \mathrm {GeV}$ as described above, where $h_2$ and $h_3$ change their role. Between MC1 and MC2 we find $\Gamma (h_2 \rightarrow \tilde{\chi }_{1}^\mp \tilde{\chi }_{1}^\pm ) > \Gamma (h_3 \rightarrow \tilde{\chi }_{1}^\mp \tilde{\chi }_{1}^\pm )$, outside it is vice versa, as can be clearly observed in the left plot of Fig. 12. The suppression of the ${\mathcal CP}$-even decay (lower lines) vs. the ${\mathcal CP}$-odd decay (upper lines) is clearly visible, where at threshold the behavior follows Eqs. (9) and (10). After the threshold the decays grow roughly linear with the Higgs boson masses.

We now turn to the phase dependence of the decay width shown in S4, i.e. for $M_{H^{\pm }}= 1200\, \mathrm {GeV}$, where the right plot in Fig. 12 shows the dependence of $\Gamma (h_i \rightarrow \tilde{\chi }_{1}^\mp \tilde{\chi }_{1}^\pm )$ on $\varphi _{M_1}$. Since $M_1$ does not appear in the chargino mass matrix, the effects of varying its phase enter only via loop corrections and are extremely small. The relative corrections in S4 are the same as in the left plot.

The results for $\Gamma (h_i \rightarrow \tilde{\chi }_{2}^\mp \tilde{\chi }_{2}^\pm )$, as shown in the left plot of Fig. 13 are smaller by roughly a factor of 2 w.r.t. $\Gamma (h_i \rightarrow \tilde{\chi }_{1}^\mp \tilde{\chi }_{1}^\pm )$, largely related to the kinematic suppression. At $M_{H^{\pm }}= 1400\, \mathrm {GeV}$ the full one-loop corrections to the $h_2$ decay reach $\sim$ $+4\,\%$. For the decay of the $h_3$ at $M_{H^{\pm }}= 1400\, \mathrm {GeV}$ we find full corrections at the level of less than $+1\,\%$. As in the upper left plot one can observe the MC2 with an “interchange” of $h_2$ and $h_3$. The same suppression of the ${\mathcal CP}$-even vs. the ${\mathcal CP}$-odd decay, as in Fig. 14 is clearly visible.

In the right plot of Fig. 13 we show the complex phase $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 1400\, \mathrm {GeV}$. The variation with $\varphi _{M_1}$ is extremely small (for the same reasons as explained above), therefore the full relative corrections in S5 are the same as in the left plot; see above.

The results for the “mixed” decay, $\Gamma (h_i \rightarrow \tilde{\chi }_{1}^\mp \tilde{\chi }_{2}^\pm )$, are shown in Fig. 14, where in the left (right) plot we show the dependence on $M_{H^{\pm }}$ ($\varphi _{M_1}$). In the left plot the first dip in the $h_2$ decay (lower lines) is the threshold TN10; see Table 5. The remaining dip (at $M_{H^{\pm }}\approx 1268\, \mathrm {GeV}$) is caused by the two thresholds TN11 and TN12. At $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ the full one-loop corrections to the $h_2$ decay reach $\sim$ $+20\,\%$. Now we turn to the corresponding $h_3$ decay. The first dip (hardly visible in the upper lines) is the threshold TN8. The second dip is the same as for the $h_2$ decay; see above. For the decay of $h_3$ at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ we find full corrections at the level of $+10\,\%$. As in Fig. 12 one can observe the MC2 with an “interchange” of $h_2$ and $h_3$.

In the right plot of Fig. 14 one can see that the variation with $\varphi _{M_1}$ is again very small with tiny ${\mathcal CP}$-asymmetries and the same corrections as in the left plot (for the same reasons as explained above).

Overall, for the neutral Higgs decays to a chargino pair we observe, again as expected, an increasing decay width $\propto M_{H^{\pm }}$, as $m_{h_{2,3}}$ increase nearly linearly with our input parameter $M_{H^{\pm }}$. The full one-loop corrections reach a level of $10\,\%$ for decay widths being of $\mathcal{O}(1\, \mathrm {GeV})$, and they can reach up to $20\,\%$ in the “mixed” decay mode. The variation with $\varphi _{M_1}$ is found to be negligible, as expected, since $M_1$ enters only via the loop corrections.

4.3.4 $h_i$ decays into neutralinos

Next we consider $h_i$ decays into neutralinos with equal indices. First, we present the decay $h_1 \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{1}^0$ in Fig. 15. Bounds on $m_{\tilde{\chi }_{1}^0}$ often assume an underlying GUT based on a simple Lie group, leading to $M_1 = 5/3 (s_{\mathrm {w}}/c_{\mathrm {w}})^2 M_2$. If the latter assumption is dropped, hardly any direct bound on $m_{\tilde{\chi }_{1}^0}$ can be placed [52]. Therefore, we also treat $M_1$ as an independent parameter. The decay $h_1 \rightarrow \tilde{\chi }_{1}^0\tilde{\chi }_{1}^0$ constitutes an invisible decay of the light Higgs boson, where bounds based on a combination of LHC and Tevatron data yield an upper bound on an invisible branching ratio of $\sim$ $40\,\%$ [119]. Since the $\tilde{\chi }_{1}^0$ constitutes a perfect Dark Matter candidate in the MSSM [50, 51], in order to determine the dark matter properties a precision measurement of this process at the LHC or a future $e^+e^-$ collider will be necessary. Consequently, a precise prediction of $\Gamma (h_1 \rightarrow \tilde{\chi }_{1}^0\tilde{\chi }_{1}^0)$ is of particular interest.

In the upper left plot of Fig. 15 we show the results for $M_{H^{\pm }}$ varying in S1, but with $|M_1| = 50\, \mathrm {GeV}$ as the base scenario. The full loop corrections are $\sim$ $+25\,\%$ at $M_{H^{\pm }}= 700\, \mathrm {GeV}$ in the upper left plot. $\varphi _{M_1}$ is varying in the upper right plot. One can observe a strong dependence of the decay width on $\varphi _{M_1}$, which can change by a factor of 8. The largest loop corrections are found as $\sim$ $+31\,\%$ for $\varphi _{M_1}= 72^\circ , 288^\circ$ and $\sim$ $+59\,\%$ at $\varphi _{M_1}= 180^{\circ }$. In the lower left plot of Fig. 15 we show the decay width with $M_1$ varying. Close to $M_1 = 0$ the lightest neutralino becomes massless. For not too small values a decay width of $\sim$ $10^{-4}\, \mathrm {GeV}$ can be observed, going to zero at the kinematic threshold. The one-loop corrections reach up to $\sim$ $+30\,\%$ at $M_1 = 20\, \mathrm {GeV}$. Finally, in the lower right plot $|\mu |$ is varying, and the decay width drops down to $\sim$ $10^{-5}\, \mathrm {GeV}$ for $\mu > 600\, \mathrm {GeV}$ and with corrections between $\sim$ $+6$ and $\sim$ $+28\,\%$.

We now turn to the decays of the heavy neutral Higgs bosons. In Fig. 16 we present the results for the decays $h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{1}^0$ ($i = 2,3$). The dependence on $M_{H^{\pm }}$ is shown in the left plot, whereas the dependence on $\varphi _{M_1}$ for $M_{H^{\pm }}= 700\, \mathrm {GeV}$ is given in the right plot. We start with $\Gamma (h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{1}^0)$ in the left plot. The first dip (lower lines) in the $h_2$ decay is the threshold TN1; see Table 5. The second dip (hardly visible in the upper lines) is the threshold TN4.¹⁴ The third “apparently single” dip is (again) in reality coming from the thresholds TN6 and TN7. The fourth (large) dip is the threshold TN10. The last “apparently single” dip is in reality coming from the thresholds TN11 and TN12. The full loop corrections are $\sim$ $+11\,\%$ at $M_{H^{\pm }}= 700\, \mathrm {GeV}$. Also shown in this plot is the decay $h_3 \rightarrow \tilde{\chi }_{1}^0\tilde{\chi }_{1}^0$. The first dip (upper lines) is in reality coming from the thresholds TN2 and TN3. The second dip (lower lines) in the $h_3$ decay is the threshold TN5. The third dip (lower lines) is the threshold TN8 and the last dip is the threshold TN9. The full relative corrections reach $\sim$ $+10\,\%$ at $M_{H^{\pm }}= 700\, \mathrm {GeV}$. The suppression of the ${\mathcal CP}$-even decay [lower lines, according to Eq. (10) at threshold, and then roughly linear with $m_{h_{2}}$] vs. the ${\mathcal CP}$-odd decay (upper lines, according to Eq. (9) at threshold, and then roughly linear with $m_{h_{3}}$) is again clearly visible.

In the right plot of Fig. 16 we show the $h_2$ decay with the complex phase $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 700\, \mathrm {GeV}$. The variation with $\varphi _{M_1}$ is found to be very large, changing the decay width by up to a factor of 5 where the full relative corrections are up to $\sim$ $+20\,\%$ at $\varphi _{M_1}= 180^{\circ }$ for S1. The $h_3$ decay with the complex phase $\varphi _{M_1}$ shows also a very large variation at $M_{H^{\pm }}= 700\, \mathrm {GeV}$ and the loop corrections reach up to $\sim$ $+19\,\%$ at $\varphi _{M_1}= 180^\circ$.

In Fig. 17 we show the decays $h_i \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{2}^0$, in full analogy to Fig. 16. The same behavior of $h_2$ and $h_3$ concerning MC1 and MC2, as well as the ${\mathcal CP}$-even and ${\mathcal CP}$-odd decay can be observed. The dips (some are hardly visible) are the same as already described in Fig. 16 beginning at $M_{H^{\pm }}\approx 1092\, \mathrm {GeV}$; see above. The full relative corrections for the $h_2$ ($h_3$) decay are $\sim$ $-18\,\%$ ($\sim$ $+10\,\%$) at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$, i.e. S4.

In the right plot of Fig. 17 we show the variation of $\Gamma (h_2 \rightarrow \tilde{\chi }_{2}^0\tilde{\chi }_{2}^0)$ with $\varphi _{M_1}$ at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$. Here the loop corrections can vary between $\sim$ $-18\,\%$ for $\varphi _{M_1}= 0^\circ , 360^\circ$ and $\sim$ $-13\,\%$ at $\varphi _{M_1}= 180^{\circ }$. The $h_3$ decay with $\varphi _{M_1}$ varying reach $\sim$ $+11\,\%$ for $\varphi _{M_1}\sim 90^\circ , 270^{\circ }$ in S4.

Next, in Fig. 18 we present the decays $h_i \rightarrow \tilde{\chi }_{3}^0 \tilde{\chi }_{3}^0$, in full analogy to Fig. 16. The same behavior of $h_2$ and $h_3$ concerning MC1 and MC2 and the ${\mathcal CP}$-even/-odd decay can be observed. The dips (some are hardly visible) are again the same as described in Fig. 16 beginning at $M_{H^{\pm }}\approx 1092\, \mathrm {GeV}$; see above. The “knee” at $M_{H^{\pm }}\approx 1545\, \mathrm {GeV}$ (red line) is the threshold TN13 (see Table 5) in the $C$-functions $C_{0,1,2}(m_{\tilde{\chi }_{3}^0}^2,m_{h_{2}}^2m_{\tilde{\chi }_{3}^0}^2,m_t^2,m_{\tilde{t}_{2}}^2,m_{\tilde{t}_{2}}^2)$. The full one-loop corrections for the $h_2$ decay are $\sim$ $+172\,\%$ at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$. This strange behavior is a numerical effect caused by an interplay of anomalous thresholds in $C_{0,1,2}(m_{\tilde{\chi }_{3}^0}^2,m_{h_{2}}^2,m_{\tilde{\chi }_{3}^0}^2,m_t^2,m_{\tilde{t}_{s^{}}}^2,m_{\tilde{t}_{s^\prime }}^2)$ ($s^{}\ne s^\prime$) with the effects induced by the Higgs mixing matrix $\hat{\mathbf {Z}}$. This effect is absent in the decay of the $h_3$, where we find the full relative corrections at the level of $\sim$ $+25\,\%$ for $M_{H^{\pm }}= 1200\, \mathrm {GeV}$.

In the right plot of Fig. 18 we show the variation of $\Gamma (h_2 \rightarrow \tilde{\chi }_{3}^0\tilde{\chi }_{3}^0)$ with $\varphi _{M_1}$ at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ (i.e. at an “extreme” point for the $h_2$ decay). Here (for the same reasons as in the left plot) the loop corrections reach $\sim$ $+111\,\%$ at $\varphi _{M_1}= 180^{\circ }$. Also in the right plot of Fig. 18 we show $\Gamma (h_3 \rightarrow \tilde{\chi }_{3}^0\tilde{\chi }_{3}^0)$ with $\varphi _{M_1}$ varying in S4. Here the loop corrections can reach $\sim$ $+26\,\%$ at $\varphi _{M_1}= 90^{\circ }, 270^{\circ }$.

In Fig. 19 we present the decays $h_i \rightarrow \tilde{\chi }_{4}^0 \tilde{\chi }_{4}^0$, again in full analogy to Fig. 16. The same behavior of $h_2$ and $h_3$ concerning MC2 and the ${\mathcal CP}$-even/-odd decay can be observed. The full relative corrections for the $h_2$ decay are $\sim$ $+4\,\%$ at $M_{H^{\pm }}= 1400\, \mathrm {GeV}$, i.e. S5, while the $h_3$ decay shows relative corrections less than $+1\,\%$ at $M_{H^{\pm }}= 1400\, \mathrm {GeV}$.

In the right plot of Fig. 19 we show $\Gamma (h_{2,3} \rightarrow \tilde{\chi }_{4}^0\tilde{\chi }_{4}^0)$ at $M_{H^{\pm }}= 1400\, \mathrm {GeV}$. For both decays the variation of $\varphi _{M_1}$ is very small, i.e. the loop corrections reach the same values (in S5) as in the left plot.

We now turn to the neutral Higgs decays to neutralinos with different indices. In this case, contrary to the decay into identical charginos, the ${\mathcal CP}$-asymmetries are also zero, due to the Majorana nature of the neutralinos.

In Fig. 20 we present the decay $h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{2}^0$. In the left plot we show the results as a function of $M_{H^{\pm }}$. The dips are (again) the same as already described in Fig. 16 beginning at $M_{H^{\pm }}\approx 948\, \mathrm {GeV}$; see above. The full relative corrections for the $h_2$ decay are $\sim$ $+9\,\%$ at $M_{H^{\pm }}= 900\, \mathrm {GeV}$ (i.e. S2). The full one-loop corrections for the $h_3$ decay at $M_{H^{\pm }}= 900\, \mathrm {GeV}$ reach $+7\,\%$.

In the right plot of Fig. 20 we show the $h_i$ decay with the complex phase $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 900\, \mathrm {GeV}$. The variation with $\varphi _{M_1}$ is found to be very large and the loop corrections vary between $\sim$ $+9\,\%$ for $\varphi _{M_1}\sim 0^\circ$ and $\sim$ $+6\,\%$ at $\varphi _{M_1}= 90^{\circ }$. We also show the $h_3$ decay in the right plot of Fig. 20 with $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 900\, \mathrm {GeV}$. The variation with $\varphi _{M_1}$ is yet larger than in the $h_2$ case. The full corrections can reach $\sim$ $+10\,\%$ at $\varphi _{M_1}= 180^{\circ }$. The general behavior can be understood as follows. For $\varphi _{M_1}= 0^\circ$ one finds ${\mathcal CP}(h_2 \tilde{\chi }_{1}^0\tilde{\chi }_{2}^0) = -{\mathcal CP}(h_3 \tilde{\chi }_{1}^0\tilde{\chi }_{2}^0) = +1$, leading to the above discussed suppression of the $h_2$ decay; see Eqs. (9) and (10). Going to $\varphi _{M_1}= 180^\circ$ changes the ${\mathcal CP}$-nature of the $\tilde{\chi }_{1}^0$, leading to ${\mathcal CP}(h_2 \tilde{\chi }_{1}^0\tilde{\chi }_{2}^0) = -{\mathcal CP}(h_3 \tilde{\chi }_{1}^0\tilde{\chi }_{2}^0) = -1$ and the corresponding suppression of the $h_3$ decay.

In Fig. 21 we present the decay $h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{3}^0$. It should be noted that the decay $h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{3}^0$ looks quite similar to Fig. 20 but with an interchange of $h_2$ with $h_3$. In the left plot we show the results as a function of $M_{H^{\pm }}$. The dips are (again) the same as already described in Fig. 16 beginning at $M_{H^{\pm }}\approx 948\, \mathrm {GeV}$; see above. The full one-loop corrections for the $h_2$ decay reach $\sim$ $+7\,\%$ at $M_{H^{\pm }}= 900\, \mathrm {GeV}$ (i.e. S2). The relative corrections for the $h_3$ decay at $M_{H^{\pm }}= 900\, \mathrm {GeV}$ are $+14\,\%$. In comparison with Fig. 20 one can observe an “inversion” of the relative size of the decays widths of the $h_2$ and the $h_3$ (green/red lines vs. blue/purple lines). This “inversion” is due to the fact that ${\mathcal CP}(\tilde{\chi }_{1}^0\tilde{\chi }_{2}^0) = -{\mathcal CP}(\tilde{\chi }_{1}^0\tilde{\chi }_{3}^0)$.

In the right plot of Fig. 21 we show the $h_i$ decay with the complex phase $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 900\, \mathrm {GeV}$. This variation is (again) found to be very large, as can be seen in the right plot. The loop corrections for the $h_2$ decay can reach $\sim$ $+9\,\%$ at $\varphi _{M_1}= 180^{\circ }$. In the right plot of Fig. 21 we show also the $h_3$ decay with $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 900\, \mathrm {GeV}$. There the loop corrections vary between $\sim$ $+14\,\%$ for $\varphi _{M_1}\sim 0^\circ$ and $\sim$ $+7\,\%$ at $\varphi _{M_1}= 90^{\circ }$. Again the “inversion” (as in the left plot) can be observed.

In Fig. 22 we present the results for $\Gamma (h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{4}^0)$ as a function of $M_{H^{\pm }}$ in the left plot. The tree-level decay width happens to be very small for the parameter set chosen; see Table 3. Because of this smallness, the relative size of the one-loop correction becomes larger then the tree level, and it can even turn negative. Therefore, in this case we added $|\mathcal{M}_{\text {1-loop}}|^2$ to the full one-loop result to obtain a positive decay width. The dips are (again) the same as already described in Fig. 16 beginning at $M_{H^{\pm }}\approx 948\, \mathrm {GeV}$; see above. The anomalous thresholds (“steps” in the red line) could be traced back to the $C$-functions at

$$\begin{aligned}&M_{H^{\pm }}\approx 1020\, \mathrm {GeV}: C_{0,1,2}\left( m_{h_{2}}^2,m_{\tilde{\chi }_{4}^0}^2,m_{\tilde{\chi }_{1}^0}^2,m_{\tilde{\chi }_{3}^0}^2,m_{\tilde{\chi }_{3}^0}^2,M_Z^2\right) , \\&M_{H^{\pm }}\approx 1026\, \mathrm {GeV}: C_{0,1,2}\left( m_{h_{2}}^2,m_{\tilde{\chi }_{4}^0}^2,m_{\tilde{\chi }_{1}^0}^2,m_{\tilde{\chi }_{2}^\pm }^2,m_{\tilde{\chi }_{1}^\pm }^2,M_W^2\right) , \\&M_{H^{\pm }}\approx 1031\, \mathrm {GeV}: C_{0,1,2}\left( m_{\tilde{\chi }_{1}^0}^2,m_{h_{2}}^2,m_{\tilde{\chi }_{4}^0}^2,m_b^2,m_{\tilde{b}_{2}}^2,m_{\tilde{b}_{1}}^2\right) , \\&M_{H^{\pm }}\approx 1035\, \mathrm {GeV}: C_{0,1,2}\left( m_{h_{2}}^2,m_{\tilde{\chi }_{4}^0}^2,m_{\tilde{\chi }_{1}^0}^2,m_{\tilde{\chi }_{4}^0}^2,m_{\tilde{\chi }_{2}^0}^2,m_{h_{1}}^2\right) , \\&M_{H^{\pm }}\approx 1182\, \mathrm {GeV}: C_{0,1,2}\left( m_{\tilde{\chi }_{1}^0}^2,m_{h_{2}}^2,m_{\tilde{\chi }_{4}^0}^2,m_t^2,m_{\tilde{t}_{2}}^2,m_{\tilde{t}_{1}}^2\right) , \end{aligned}$$

in this order. The full relative corrections for the $h_2$ ($h_3$) decay are $\sim$ $-77\,\%$ ($\sim$ $-93\,\%$) at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ (i.e. S4).

In the right plot of Fig. 22 we show $\Gamma (h_i \rightarrow \tilde{\chi }_{1}^0 \tilde{\chi }_{4}^0)$ with the complex phase $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$. Here (for the same reasons as in the left plot) the loop corrections can be larger than the tree level (and for consistency with the left plot we also add $|\mathcal{M}_{\text {1-loop}}|^2$ here). The loop corrections for the $h_2$ decay vary between $\sim$ $-77\,\%$ at $\varphi _{M_1}\sim 0^\circ , 360^\circ$ and $\sim$ $-44\,\%$ at $\varphi _{M_1}= 180^{\circ }$. The loop corrections for the $h_3$ decay vary between $\sim$ $-93\,\%$ at $\varphi _{M_1}\sim 0^\circ , 360^\circ$ and $\sim$ $-78\,\%$ at $\varphi _{M_1}= 180^{\circ }$.

In Fig. 23 we present the decay $h_i \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{3}^0$. In the left plot we show the results as a function of $M_{H^{\pm }}$. The dips (some are hardly visible) are again the same as already described in Fig. 16 beginning at $M_{H^{\pm }}\approx 1092\, \mathrm {GeV}$; see above. The full relative corrections for the $h_2$ decay reach up to $\sim$ $+59\,\%$ at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ (i.e. S4). The loop corrections for the $h_3$ decay at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ are $\sim$ $-14\,\%$.

In the right plot of Fig. 23 we show the $h_i$ decay with the complex phase $\varphi _{M_1}$ varying at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$. For the $h_2$ decay the variation of $\varphi _{M_1}$ is very small, i.e. the loop corrections reach (in S4) the same values ($\sim$ $+59\,\%$) for all $\varphi _{M_1}$. The variation of $\varphi _{M_1}$ in the $h_3$ decay is also small with corrections at the level of $\sim$ $-14\,\%$.

In Fig. 24 we show the decay $h_i \rightarrow \tilde{\chi }_{2}^0 \tilde{\chi }_{4}^0$. In the left plot we show the results as a function of $M_{H^{\pm }}$. The dips are (again) the same as already described in Fig. 16 beginning at $M_{H^{\pm }}\approx 1171\, \mathrm {GeV}$; see above. The full relative corrections for the $h_2$ decay reach up to $\sim$ $+15\,\%$ at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$, i.e. S4. The loop corrections for the $h_3$ decay at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ are $\sim$ $+9\,\%$

In the right plot of Fig. 24 the $h_i$ decay is shown with the complex phase $\varphi _{M_1}$ varying in S4. For both decays the variation of $\varphi _{M_1}$ is very small, as expected, since $\tilde{\chi }_{2}^0$ and $\tilde{\chi }_{4}^0$ are determined largely by $M_2$ and $\mu$ in the neutralino mass matrix (for the parameters chosen as in Table 3). The loop corrections for the $h_2$ ($h_3$) decay reach $\sim$ $+16\,\%$ ($\sim$ $+9\,\%$) at $\varphi _{M_1}= 180^{\circ }$.

The final decays involving neutralinos are shown in Fig. 25. The results as a function of $M_{H^{\pm }}$ are given in the left plot. The dips are (again) the same as already described in Fig. 16 beginning at $M_{H^{\pm }}\approx 1171\, \mathrm {GeV}$; see above. The full relative corrections are only $\sim$ $+3\,\%$ at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ (i.e. S4). The full relative corrections at $M_{H^{\pm }}= 1200\, \mathrm {GeV}$ reach $+6\,\%$. In comparison with Fig. 24 one can observe (again) an “inversion” of the relative size of the decays widths of the $h_2$ and the $h_3$, due to the fact that ${\mathcal CP}(\tilde{\chi }_{2}^0\tilde{\chi }_{4}^0) = -{\mathcal CP}(\tilde{\chi }_{3}^0\tilde{\chi }_{4}^0)$.

In the right plot of Fig. 25 we show the $h_i$ decay with the complex phase $\varphi _{M_1}$ varying in S4. For both decays the variation of $\varphi _{M_1}$ is again very small, since both neutralinos are largely determined by $\mu$ (for the parameters chosen as in Table 3). The full one-loop corrections are the same as for the left plot.

Overall, for the neutral Higgs decays to a neutralino pair we observed, again as expected, an increasing decay width $\propto m_{h_{i}}$.¹⁵ The full one-loop corrections reach a level of 10–20 % for decay widths of $\mathcal{O}(1\, \mathrm {GeV})$. The variation with $\varphi _{M_1}$ is found largest in the cases where the ${\mathcal CP}$-nature of the decay depends strongly on the phase, there then changes by a factor of 5 or more can be observed.

5 Conclusions

We evaluated all partial decay widths corresponding to a two-body decay of the MSSM Higgs bosons to charginos and neutralinos, allowing for complex parameters. In the case of the discovery of additional Higgs bosons a subsequent precision measurement of their properties will be crucial to determine their nature and the underlying (SUSY) parameters. In order to yield a sufficient accuracy, one-loop corrections to the various Higgs-boson decay modes have to be considered. In this work we take another step in the direction of completion of the calculation of all two-body decays at the one-loop level in the cMSSM in this stable and reliable renormalization scheme: we calculated all two-body decay modes of the Higgs bosons to charginos and neutralinos in the cMSSM.

The decay modes are given in Eqs. (1)–(3). The evaluation is based on a full one-loop calculation of all decay channels, also including hard and soft QED radiation. We restricted ourselves to a version of our renormalization scheme which is valid for $|M_1| < |M_2|, |\mu |$ and $M_2 \ne \mu$ [where $M_1$ and $M_2$ denote the soft SUSY-breaking parameters of the $U(1)$ and $\mathrm{SU}(2)$ gauginos, and $\mu$ is the Higgs mixing parameter] to simplify the analysis, even though our setup allows one to switch to other parameter regions, possibly implying a different renormalization; see the discussion in Refs. [63–65].

We first reviewed the relevant sectors including some details on the one-loop renormalization procedure of the cMSSM, which are relevant for our calculation. In most cases we follow Ref. [62]. However, in the scalar fermion sector, where we differ from Ref. [62] the relevant details are indicated. We have discussed the calculation of the one-loop diagrams, the treatment of UV and IR divergences that are canceled by the inclusion of (hard and soft) QED radiation. We have checked our result against the literature, and in most cases we have found good agreement, once our setup was changed to the one used in the existing analyses.

While the analytical calculation has been performed for all decay modes to charginos and neutralinos, in the numerical analysis we mostly concentrated on the decays of the heavy Higgs bosons, with $h_1 \rightarrow \tilde{\chi }_{1}^0\tilde{\chi }_{1}^0$ being the only channel analyzed for the light neutral Higgs boson. For the analysis we have chosen a parameter set that allows simultaneously for a maximum number of two-body chargino/neutralino decay modes. In the analysis either the charged Higgs boson mass or the phase of $M_1$ has been varying. For $M_{H^{\pm }}$ we investigated an interval starting at $M_{H^{\pm }}= 600\, \mathrm {GeV}$ up to $M_{H^{\pm }}= 1.6\, \mathrm {TeV}$, which roughly coincides with the reach of the LHC for high-luminosity running as well as an $e^+e^-$ collider with a center-of-mass energy up to $\sqrt{s} \sim 3\, \mathrm {TeV}$.

In our numerical scenarios we compared the tree-level partial decay widths with the full one-loop corrected partial decay widths. We concentrated on the analysis of the decay widths themselves, since the size of the corresponding branching ratios (and thus the size of their one-loop effects) is highly parameter dependent.

We found sizable corrections of $\sim$ $10\,\%$ in many channels, sometimes going up to $\sim$ $20\,\%$. Even larger corrections are only found in the cases where the tree-level result happens to be small and thus the decay likely not observable. Corrections at the 10–20 % level have also been found for the decay $h_1 \rightarrow \tilde{\chi }_{1}^0\tilde{\chi }_{1}^0$, which could constitute an important channel for the determination of the dark matter properties in the cMSSM. Consequently, the full one-loop corrections should be taken into account for the interpretation of the searches for charginos/neutralinos as well as for any future precision analyses of those decays.

The tree-level results, but also the size of the full one-loop corrections, often depend strongly on the complex phase analyzed, $\varphi _{M_1}$. The one-loop contributions can vary by a factor of $\sim$ $2$ as a function of the complex phase. Neglecting the phase dependence could lead to a wrong impression of the relative size of the various decay widths.

In the cases where a decay and its complex conjugate final state are possible, i.e. the charged Higgs decays, we have evaluated both decay widths independently. The asymmetries, as a byproduct of our calculation, turn out to be relatively small, at the level of a few per-cent.

The numerical results we have shown are, of course, dependent on the choice of the SUSY parameters. Nevertheless, they give an idea of the relevance of the full one-loop corrections. Decay channels (and their respective one-loop corrections) that may look unobservable due to the smallness of their decay width in our numerical examples could become important if other channels are kinematically forbidden. Following our analysis it is evident that the full one-loop corrections are mandatory for a precise prediction of the various branching ratios. The full one-loop corrections should be taken into account in any precise determination of (SUSY) parameters from the decay of (heavy) MSSM Higgs bosons. There are plans to implement the evaluation of the branching ratios of the (heavy) Higgs bosons into the Fortran code FeynHiggs, together with an automated choice of the renormalization scheme valid for the full cMSSM parameter space.