Inflationary cosmology from quantum conformal gravity

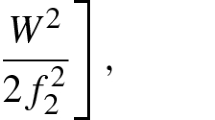
Abstract

We analyze the functional integral for quantum conformal gravity and show that, with the help of a Hubbard–Stratonovich transformation, the action can be broken into a local quadratic-curvature theory coupled to a scalar field. A one-loop effective-action calculation reveals that strong fluctuations of the metric field are capable of spontaneously generating a dimensionally transmuted parameter which, in the weak-field sector of the broken phase, induces a Starobinsky-type f(R)-model with a gravi-cosmological constant. A resulting non-trivial relation between Starobinsky’s parameter and the gravi-cosmological constant is highlighted and implications for cosmic inflation are briefly discussed and compared with the recent PLANCK and BICEP2 data.

1 Introduction

The idea that Einstein’s gravity may be considered as a large-distance effective theory arising from a spontaneous or dynamical symmetry breakdown in some underlying scale-invariant quantum field theory dates back to work of Minkowski [1], Smolin [2], Adler [3, 4], Zee [5], Spokoiny [6], Kleinert and Schmidt [7], and others (see, e.g., Ref. [8] for recent review), even though the motivations can be traced back to seminal papers in the 1960s of Zeldovich [9] and Sakharov [10]. The ensuing mechanisms for symmetry breaking are realized typically by spontaneously breaking a scale invariance in appropriate scale-invariant quantum field theory propagating in a curved spacetime [3, 4] or by a conformal gravity (CG) which is dynamically broken via additional scalar fields [11, 12].

In particular, CG has recently attracted renewed attention because local conformal invariance seems to be the key component in a number of cosmological models. This activity was substantially fueled by Mannheim et al.’s no-ghosts result [13–15],¹ $^{,}$ ² Smilga’s benign-ghost result [20], new non-perturbative approaches [21], and by related work on the conformal anomaly [22]. The CG has since been revisited from various points of view, e.g., as an alternative to standard Einstein gravity giving a (partial) resolution of a flatness problem [23], or as an explanatory frame for missing matter in galaxies [24] and a possibly vanishing cosmological constant [25]. The CG has also been explored recently in a number of theoretical and observational frameworks including conformal supergravity [26], twistor–string theory [27], asymptotic safety theories [28, 29], black-hole complementarity issue [19], AdS/CFT correspondence [30], and the type Ia supernova (SNIa) and H(z) observational data [31].

Unfortunately, the particle spectrum of CG does not contain (at least not on-shell) a scalar field. In fact, CG has six (on-shell) propagating degrees of freedom: the massless spin-2 graviton, massless spin-1 vector boson, and massless spin-2 ghost field [26, 32]. Should the Einstein gravity be induced within CG at low energies, the absence of a fundamental scalar poses immediately two problems: (a) it is difficult to break a conformal symmetry (either spontaneously or dynamically) without a fundamental spinless boson [26]; (b) the scalar degree of freedom is of a central importance to generate correct primordial density perturbations during inflation [8]. For these reasons an external scalar field is sometimes artificially coupled to CG [11, 12]. In this paper we wish to point out the subtle fact that a non-dynamical spurion scalar field can be introduced in CG via the Hubbard–Stratonovich transformation without spoiling the particle spectrum, (non-perturbative) unitarity, and renormalizability of CG. The spurion field is actually an imprint of a scalar degree of freedom that would normally be present in the theory if the (local) conformal symmetry would not decouple it from the on-shell spectrum. The spurion field morphs into a physical scalar field (scalaron or gravi-scalar) after its kinetic term gets generated radiatively. The field then mediates a dynamical breakdown of the conformal symmetry.

In the broken phase the scalaron field acquires a non-trivial vacuum expectation value (VEV) via dimensional transmutation. The resulting low-energy behavior in the broken phase can be identified with Starobinsky’s f(R)-model (SM) with a gravi-cosmological constant or, in a dual picture, with a two-field hybrid inflationary model. A scalaron field helps to form a (composite) inflaton and assists during the inflaton decay in the reheating phase.

2 Quantum conformal gravity

CG is a pure metric theory that possesses general coordinate invariance, which augments standard gravity with the additional Weyl symmetry, i.e., invariance under a local rescaling of the metric $g_{\mu \nu }(x)\rightarrow e^{2\alpha (x)}g_{\mu \nu }(x)$, with $\alpha (x)$ being an arbitrary local function. The simplest CG action, i.e., the action with both reparametrization and Weyl invariance reads [33, 34]

$$\begin{aligned} \mathcal{A}_\mathrm{conf} = -\frac{1}{8\alpha _c^2}\int \mathrm{d}^4x\, (-g)^{1/2}C_{\lambda \mu \nu \kappa } C^{\lambda \mu \nu \kappa } . \end{aligned}$$

(1)

Here $\alpha _c$ is a dimensionless coupling constant (in natural units) and $C_{\lambda \mu \nu \kappa }$ is the Weyl tensor, which in four spacetime dimensions reads

$$\begin{aligned} C_{\lambda \mu \nu \kappa }= & {} R_{\lambda \mu \nu \kappa } {-} \left( g_{\nu [\lambda }R_{\mu ]\kappa } {-} g_{\kappa [\lambda }R_{\mu ]\nu } \right) + \frac{1}{3}R \, g_{\nu [\lambda }g_{\mu ]\kappa } , \end{aligned}$$

(2)

with $R_{\lambda \mu \nu \kappa }$ being the Riemann curvature tensor, $R_{\lambda \nu }=R_{\lambda \mu \nu }{}^\mu$ the Ricci tensor, and $R\equiv R_\mu {}^\mu$ the scalar curvature. Throughout we adopt the signature $(+,-,-,-)$ and the sign conventions of Landau–Lifshitz.

With the help of the Gauss–Bonnet theorem one can cast $\mathcal{A}_\mathrm{conf}$ into the equivalent form (modulo a topological term)

$$\begin{aligned} \mathcal{A}_\mathrm{conf} = -\frac{1}{4\alpha _c^2}\int \mathrm{d}^4x\, (-g)^{1/2}\left[ R_{\mu \kappa }R^{\mu \kappa }- \frac{1}{3} R^2\right] . \end{aligned}$$

(3)

Variation of $\mathcal{A}_\mathrm{conf}$ with respect to the metric yields Bach’s field equation [34],

$$\begin{aligned} 2D_{\lambda } D_{\kappa }C^{\mu \lambda \nu \kappa }_{} -C^{\mu \lambda \nu \kappa }R_{\lambda \kappa } \equiv B^{\mu \nu } = 0\, , \end{aligned}$$

(4)

where $B^{\mu \nu }$ is the Bach tensor and $D_{\alpha }$ the Riemannian covariant derivative.

We formally define a quantum field theory of gravity by a functional integral

$$\begin{aligned} Z = \sum _i \int _{\Sigma _i} \mathcal{D}g_{\mu \nu }\,\, {e}^{i\mathcal{A}_\mathrm{conf}}\, . \end{aligned}$$

(5)

Here $\mathcal{D}g_{\mu \nu }$ denotes the functional-integral measure, whose proper treatment involves the Faddeev–Popov gauge fixing of the gauge symmetry Diff $\times$ Weyl$(\Sigma _i)$ plus the ensuing Faddeev–Popov determinant [35]. Potential local factors $[-\det g_{\mu \nu }(x)]^{\omega }$ with Misner’s ($\omega = -5/2$) or De Witt’s ($\omega = (D-4)(D+1)/8$) indexes are omitted in the measure because they do not contribute to the Feynman rules. Their effect is to introduce terms $\omega \delta ^{(4)}(0) \int \mathrm{d} x^4 \log (-g)$ into the action, which by Veltman’s rule are set to zero in dimensional regularization. The sum in (5) is a sum over four-topologies, that is, a sum over topologically distinct manifolds $\Sigma _i$ (analogous to the sum over genus in string theory or the sum over homotopically inequivalent vacua in the Yang–Mill theory) which can potentially contain topological phase factors, e.g., Euler number of $\Sigma _i$, cf. Ref. [36].³

It should be remarked that despite the fourth-order nature of the Bach equation (4) indicating the presence of on-shell ghost states [32, 37], the recent advances in non-perturbative [21, 38–41] and PT-symmetric [13, 14, 42] techniques suggest that the would-be ghost states disappear from the energy eigenspectrum and that CG is stable (i.e., non-perturbatively unitary). Also, the conformal instability typical for the Euclidean quantum gravity is not presents in CG. A particularly pleasing aspect of the quadratic-curvature action (3) is its power-counting renormalisability⁴ and asymptotic freedom ($\beta$-function for $\alpha _c$ is negative) [44].

3 Uncompleting the $R^2$-term

Here we wish to point out that the large number of derivatives in the free graviton propagator implied by (3) makes fluctuations so violent that the theory might spontaneously create a new mass term. This phenomenon is indeed known to happen in a number of higher-derivative systems ranging from biomembranes [45–47] through string theories with extrinsic curvature [48–50], to gravity-like theories [51]. For instance, in biomembranes and stiff strings the ensuing mass term can be identified with a tension. We shall now show that an analogous mechanism spontaneously generates the Starobinsky action [52],

$$\begin{aligned} \mathcal{A}_\mathrm{St} = - \frac{1}{2\kappa ^2}\int \mathrm{d}^4x\, (-g)^{1/2} (R - \xi ^2 R^2) . \end{aligned}$$

(6)

Here $\kappa ^2 = {8 \pi G_\mathrm{N}}$ where $G_\mathrm{N} = 1/m_p^2$ is Newton’s (gravitational) constant and $m_p$ is the Planck mass. Starobinsky’s parameter $\xi$ is related to the inflational scale and by the Planck satellite data $\xi /\kappa \sim 10^5$ (cf. reference [53] for the Planck constraints on inflationary models. For a general survey of Planck results including inflation, see [54]). The minus sign in front of $R^2$-term is a consequence of the Landau–Lifshitz convention [55].

In order to see how the spontaneous generation of (6) comes about we first observe that the $R^2$-part of the action (3) is the global scale-invariant (“$\mathrm{gsi}$”) expression. This is because under an infinitesimal Weyl transformation $g_{\mu \nu } \rightarrow g_{\mu \nu } + 2\alpha (x) g_{\mu \nu }$, while $R \rightarrow [1-2\alpha (x)]R - 6 D^2 \alpha (x)$ (the covariant derivative $D_{\mu }$ is with respect to $g_{\mu \nu }$). Since $g \rightarrow [1 + 8\alpha (x)] g$, the $R^2$-term part of the action will be scale invariant provided $D^2 \alpha (x) = 0$.

The $R^2$-part of the action can be further decomposed by using the Hubbard–Stratonovich (HS) transformation [56, 57]

$$\begin{aligned} \exp (i\mathcal{A}_\mathrm{gsi})\equiv & {} \exp \left( \frac{i}{12 \alpha ^2_c} \int \mathrm{d}^4 x \, (-g)^{1/2} R^2\right) \nonumber \\= & {} \int \mathcal{D} \lambda \exp \left[ -i \int \mathrm{d}^4 x \, (-g)^{1/2} \left( \frac{3 \alpha ^2_c}{4} \!\lambda ^2 + \frac{\lambda R}{2} \right) \right] \!. \nonumber \\ \end{aligned}$$

(7)

The essence of the HS transformation is a straightforward manipulation of a Gaussian integral, which allows one to decouple quadratic (or generally quartic) terms in the action in terms of an auxiliary (bosonic) field variable whose fluctuations can in principle be described by higher loop diagrams. Due to a radiative correction the HS field can develop in the infrared regime a gradient term which then allows one to identify the HS boson with a genuine dynamical particle. A paradigmatic example of this scenario is obtained when reducing the BCS superconductivity to its low-energy effective level. There the HS boson coincides with the disordered field whose dynamics is described via the famous Ginzburg–Landau equations [58].

The HS transformation has currently a well-established place in solid-state theory [58, 59] and elementary particle physics [60–62]. It has led to a good understanding of important collective physical phenomena such as superconductivity, superfluidity of He$^3$, plasma and other charge-density waves, pion physics and chiral symmetry breaking in quark theories [63], etc.

Although the auxiliary field $\lambda (x)$ in (7) does not have a bare kinetic term, the local conformal symmetry of $\mathcal{A}_\mathrm{conf}$ allows one to rescale the metric so that a kinetic term can easily be generated. For instance, when $g_{\mu \nu } \mapsto |{\lambda }|^{-1} g_{\mu \nu }$ then $\mathcal{A}_\mathrm{gsi}$ goes to

$$\begin{aligned} \int \mathrm{d}^4 x \, (-g)^{1/2} \left( -\frac{\lambda R}{2 |\lambda |} + \frac{3 }{4 \lambda ^2} \partial _{\mu } \lambda \partial ^{\mu } \lambda - \frac{3 \alpha ^2_c}{4} \right) \! \end{aligned}$$

(8)

(and other higher-order derivatives of $\lambda$ will come from the remaining $R^{\mu \nu }R_{\mu \nu }$-term).

Since the $\lambda$-kinetic term depends on the conformal scaling, $\lambda$-kinematics is gauge dependent, implying that $\lambda$ cannot represent a physical field. On the other hand, when the conformal symmetry breaks down then the $\lambda$-field is trapped in a particular (broken) phase with specific kinetic and potential terms. This will be shown below.

To proceed, we separate the $\lambda$-field into a background field $\bar{\lambda }$ corresponding to the VEV of $\lambda$ and fluctuations $\delta \lambda$ which have only nonzero momenta. Of course, the fluctuations must be included to make the theory completely equivalent to the original (5). In the following we employ the standard effective-action strategy, i.e., we neglect all terms involving $\delta \lambda$ and take the saddle-point approximation to the remaining integral over $\bar{\lambda }$.

As will be seen shortly, $\lambda$ spontaneously develops a positive VEV, so that the sign of the R-term in (7) coincides with the sign of the Einstein term. Since we expect that our theory will eventually induce Einstein’s action (at least at low enough energies) it is convenient to rescale $\lambda \rightarrow \lambda /\kappa ^2$.

With the benefit of hindsight we further introduce an arbitrary mixing angle $\theta$ and write formally $\mathcal{A}_\mathrm{gsi} = C^2 \mathcal{A}_\mathrm{gsi} - S^2 \mathcal{A}_\mathrm{gsi}$ where $C\equiv \cosh \theta$, $S\,\equiv \sinh \theta$. Applying the HS transformation only to the $(S^2 \mathcal{A}_\mathrm{gsi})$-part we get, after a formal replacement $\alpha _c^2 \rightarrow -\alpha _c^2/S^2$ in (7),

$$\begin{aligned} \mathcal{A}_\mathrm{gsi}= & {} \frac{C^2}{12\alpha _c^2}\!\int \mathrm{d}^4x\, (-g)^{1/2} R^2 - \frac{1}{2\kappa ^2}\!\int \mathrm{d}^4x\, (-g)^{1/2} \lambda R \nonumber \\&+ \ \frac{3\alpha _c^2}{4S^2\kappa ^4}\!\int \mathrm{d}^4x\, (-g)^{1/2} \lambda ^2 . \end{aligned}$$

(9)

Let us now show that the fluctuations of the metric $g_{\mu \nu }$ can achieve the aforementioned scenario. In particular, we find a set of parameters in the model parameter space for which $\bar{\lambda }\equiv \langle \lambda \rangle =1$. As a result, the long-range behavior of our theory will coincide with that of Starobinsky’s f(R)-model.

4 Emergence of Starobinsky’s model

We proceed by splitting the spacetime metric into the flat Minkowski background plus a fluctuation $h_{\mu \nu }$ defined by $g_{\mu \nu }=\eta _{\mu \nu } + \alpha _c h_{\mu \nu }$ (realizing that $\alpha _c \sim C \kappa /\xi$), and then expanding the Lagrangian in (3) [including the explicit form (9)] to the second order in $\alpha _c$. Omitting total derivatives, using the weak-field relations of Appendix A and setting $\lambda = \bar{\lambda }$, we end up with the following outcome ($\square \equiv \partial ^2$):

$$\begin{aligned} -\mathcal{A}_\mathrm{conf}= & {} \frac{1}{16} \int \mathrm{d}^4x h^{\mu \nu } \square ^2 h_{\mu \nu } - \frac{1}{8} \int \mathrm{d}^4x \partial _{\lambda } h^{\lambda \mu } H_{\mu \nu } \partial _{\rho } h^{\rho \nu }\nonumber \\&+ \frac{1}{4}\left( \frac{1}{4} -\frac{C^2}{3}\right) \int \mathrm{d}^4x \bar{h} \square ^2 \bar{h}\nonumber \\&+ \frac{1}{2\kappa ^2} \int \mathrm{d}^4x \left( { - \alpha _c\bar{\lambda } \square \bar{h}} - \frac{{\alpha }_c^2}{4 }\bar{h} \bar{\lambda } \square \bar{h} \right. \nonumber \\&- \left. \frac{\alpha _c^2}{2}\partial _{\lambda } h^{\lambda \mu } \bar{\lambda } \square ^{-1}H_{\mu \nu } \partial _{\rho } h^{\rho \nu } + \frac{\alpha _c^2}{4} h^{\mu \nu } \bar{\lambda } \square h_{\mu \nu }\right) \nonumber \\&- \frac{3\alpha _c^2}{4S^2\kappa ^4} \int \mathrm{d}^4x \bar{\lambda }^2 \nonumber \\= & {} \int \mathrm{d}^4x h^{\mu \nu } \mathfrak {A}\square ^2 h_{\mu \nu } + \int \mathrm{d}^4x \partial _{\lambda } h^{\lambda \mu } \mathfrak {B} H_{\mu \nu } \partial _{\rho } h^{\rho \nu }\nonumber \\&+ \int \mathrm{d}^4x \bar{h} \mathfrak {C} \square ^2 \bar{h} + \frac{3\alpha _c^2}{4S^2\kappa ^4} \int \mathrm{d}^4x \bar{\lambda }^2 \, , \nonumber \\ \mathfrak {A}= & {} 1/16 + \alpha _c^2 \bar{\lambda } \square ^{-1}/(8 \kappa ^2),\quad \mathfrak {B} = -\mathfrak {A}/2,\nonumber \\ \mathfrak {C}= & {} \frac{1}{4}\left( \frac{1}{4}- \frac{C^2}{3}\right) - \alpha _c^2 \bar{\lambda } \square ^{-1}/(8 \kappa ^2)\, , \end{aligned}$$

(10)

where $H_{\mu \nu } = 1/2 \partial _{\mu }\partial _{\nu } - \square \eta _{\mu \nu }$ and $\bar{h} = h^{\mu }_{\mu } - \partial _{\mu } \square ^{-1}\partial _{\nu } h^{\mu \nu }$.

A phenomenologically consistent long-range behavior of the gravitational field is ensured if $\bar{\lambda }=1$. To see that such a solution exists at energies low enough, we calculate the one-loop contribution to the Minkowski effective action. This is obtained by functionally integrating out the fields $h_{\mu \nu }$ in the exponential $e^{i\mathcal{A}_\mathrm{conf}}$ in which $\lambda$ is approximated by its VEV, i.e., $\bar{\lambda }$. The result is $e^{-i\varOmega _4 V_\mathrm{{eff}}}$, where $\varOmega _4$ is the total four-volume of the universe, and $V_\mathrm{{eff}}$ is the effective potential. The form (10) is particularly convenient for the gauge fixings [11, 26]: $\chi ^{\nu } \equiv \partial _{\mu } h^{\mu \nu } = \zeta ^{\nu }(x)$ (coordinate gauge) and $\chi \equiv \bar{h} = \zeta (x)$ (conformal gauge). Here $\zeta ^{\nu }(x)$ and $\zeta (x)$ are arbitrary functions of x. Using ’t Hooft’s averaging trick [64]:

$$\begin{aligned} \delta [\chi - \zeta ]\rightarrow & {} \int {\mathcal {D}} \zeta e^{i\int \zeta {\mathcal {H}} \zeta } (\det {\mathcal {H}})^{1/2} \delta [\chi - \zeta ] \nonumber \\= & {} \ e^{i\int \chi {\mathcal {H}} \chi } (\det {\mathcal {H}})^{1/2} \end{aligned}$$

(11)

(${\mathcal {H}}$ is an arbitrary symmetric operator), and doing some straightforward computations, we obtain the zero-genus (fixed topology) contribution to the partition function,

$$\begin{aligned} Z_0= & {} {\mathcal {N}} (\det \mathcal {M}_\mathrm{FP}) (\det H_{\mu \nu } \det (\square ^2)_{\bar{h}})^{1/2} [\det (-\square ^2)_{h_{\mu \nu }}]^{-1/2}\nonumber \\&\times (\det \mathfrak {C})^{1/2} (\det \mathfrak {A})^{-3} e^{-i\varOmega _4 3\alpha _c^2 \bar{\lambda }^2/(4 S^2 \kappa ^4) }\nonumber \\= & {} \mathcal {N}\{[\det (-\square )]^{-1/2}\}^{6}(\det \mathfrak {C})^{1/2}(\det \mathfrak {A})^{-3} \nonumber \\&\times e^{-i\varOmega _4 3\alpha _c^2 \bar{\lambda }^2/(4 S^2 \kappa ^4)} \end{aligned}$$

(12)

[$(\mathcal {M}_\mathrm{FP})_{\mu \nu } = -\square \eta _{\mu \nu } - \partial _{\mu } \partial _{\nu }$ is the Faddeev–Popov operator for coordinate gauge].⁵ The factor $\{[\det (-\square )]^{-1/2}\}^{6}$ correctly indicates that the number of propagating modes in the linearized CG is six (cf. Ref. [32]).

From (12) the one-loop $V_\mathrm{{eff}}$ reads

$$\begin{aligned} V_\mathrm{{eff}}= & {} \frac{i}{2}\!\!\int ' \!\! \frac{{\text {d}}^Dk}{(2\pi )^D}\ln \!\left( k^2 - \frac{6\alpha _c^2 \bar{\lambda }}{\kappa ^2 (4^2 +1)}\!\right) \nonumber \\&-\frac{6i}{2} \!\!\int \!\! \frac{{\text {d}}^Dk}{(2\pi )^D}\ln \!\left( k^2 - \frac{2\alpha _c^2 \bar{\lambda }}{\kappa ^2}\!\right) - \frac{3\alpha ^2}{4S^2 \kappa ^4} \bar{\lambda }^2. \end{aligned}$$

(13)

The prime indicates a trivial subtraction of the zero mode. Note that for (assumed) $\bar{\lambda } > 0$ the ensuing massive pole is physical only when $\theta \in (-\text{ arcsinh }(1/4),\infty )$. The integral over k can be evaluated, e.g., with the help of dimensional regularization ($D=4-2\epsilon$) in which case it yields

$$\begin{aligned} V_\mathrm{{eff}}= & {} - \frac{9\alpha ^4_c\bar{\lambda }^2}{16\pi ^2\kappa ^4(4S^2 +1)^2} \left[ \ln \frac{6\alpha _c^2\bar{\lambda }}{ (1+4 S^2) \kappa ^2 \varLambda ^2} -\frac{3}{2}\right] \nonumber \\&+\frac{3\alpha ^4_c\bar{\lambda }^2}{8\pi ^2\kappa ^4} \left[ \ln \frac{2\alpha _c^2\bar{\lambda }}{\kappa ^2 \varLambda ^2} -\frac{3}{2}\right] -\frac{3\alpha ^2_c}{4S^2 \kappa ^4}\bar{\lambda }^2, \end{aligned}$$

(14)

where $\varLambda = \sqrt{4\pi } \mu e^{-\gamma /2} e^{1/2\epsilon }$, $\mu$ is an arbitrary renormalization scale, and $\gamma$ is the Euler–Mascheroni constant. To obtain a finite result as $\epsilon \rightarrow 0$ we utilize the $\overline{\text{ MS }}$ renormalization scheme. This fixes the counterterm so that

$$\begin{aligned} V_\mathrm{{eff}}= & {} - \frac{9\alpha ^4_c\bar{\lambda }^2}{16\pi ^2\kappa ^4(4S^2 + 1)^2} \left[ \ln \frac{6\alpha _c^2\bar{\lambda }}{ (1+4 S^2) \kappa ^2 \mu ^2} -\frac{3}{2}\right] \nonumber \\&+\ \frac{3\alpha ^4_c\bar{\lambda }^2}{8\pi ^2\kappa ^4} \left[ \ln \frac{2\alpha _c^2\bar{\lambda }}{\kappa ^2 \mu ^2} -\frac{3}{2}\right] - \frac{3\alpha ^2_c}{4S^2 \kappa ^4}\bar{\lambda }^2 , \end{aligned}$$

(15)

with $\mu ^2$ being the subtraction point.

The saddle point in $\bar{\lambda }$ corresponding to the VEV is determined by the vanishing of $V_{\bar{\lambda }}\equiv \partial V_\mathrm{eff}/\partial _{\bar{\lambda }}$. This yields the minimal $V_\mathrm{eff}$ for

$$\begin{aligned} \bar{\lambda }(S) \!= & {} \! \exp \left( \frac{3 \alpha _c^2 S^2 \ln \left( \frac{3}{4 S^2\!+\!1}\right) \!+\! 4 \pi ^2 (4 S^2 + 1)^2}{\alpha ^2 S^2 \left( 32 S^4+16 S^2-1\right) } \right) \frac{\kappa ^2\mu ^2 e }{2 \alpha _c^2}\, . \nonumber \\ \end{aligned}$$

(16)

In this case $V_\mathrm{eff}< 0$ for $S^2 > (\sqrt{6} -2)/8 \approx 0.056$, irrespective of the actual values of $\alpha$ and $\kappa$. A trivial solution of $V_{\bar{\lambda }} = 0$, namely $\bar{\lambda }(S) = 0$, yields $V_\mathrm{eff}= 0$ and hence it represents a local maximum (i.e., unstable solution) for the above range of $S^2$.

Although the full theory described by the action (10) is independent of the mixing angle $\theta$, the truncation of the perturbation series after a finite loop order in the fluctuating $h_{\mu \nu }$-field spoils this independence. The optimal result is obtained by utilizing the principle of minimal sensitivity [65] known from the renormalization-group calculus. The principle of minimal sensitivity is at the heart of the $\delta$-perturbation expansion (see, e.g., [66]) and variational perturbation expansion [67, 68]. There, if the perturbation theory depends on an unphysical parameter, say $\theta ,$ the best result is achieved if each order has the weakest possible dependence on the parameter $\theta$.

Consequently, at the one-loop level the value of $\theta$ is determined from the vanishing of the derivative of $V_\mathrm{{eff}}$ with respect to $S^2$. By setting $V_{S^2}\equiv \partial V_\mathrm{eff}/\partial S^2$, we have

$$\begin{aligned} \frac{{\text {d}} V_\mathrm{eff}}{{\text {d}} S^2} = \frac{\partial \bar{\lambda }(\theta )}{\partial S^2} V_{\bar{\lambda }} + V_{S^2} \ = \ V_{S^2} = 0 . \end{aligned}$$

(17)

This is equivalent to the equation

$$\begin{aligned} \frac{\left( 128 S^6 + 96 S^4 + 36 S^2-1\right) }{S^4 \left( 32 S^4+16 S^2-1\right) }\! = \! \frac{12 \alpha ^2 \ln \left( \frac{4 S^2+1}{3}\right) }{\pi ^2 \left( 32 S^4+16 S^2 -1\right) },\nonumber \\ \end{aligned}$$

(18)

which admits two branches of real solutions; either $S^2 = 0.0259237 - 0.0000197 \alpha ^2 + \mathcal {O}(\alpha ^4)$, which, however, does not give a stable $\bar{\lambda }(S)$ (as $V_\mathrm{eff} > 0$) or S should have maximally allowable value within the range of validity of our one-loop approximations. This gives the $\bar{\lambda }(S)$-stable solution $S \sim \xi /\kappa \sim 10^5$.

Consequently, from Eq. (16) we deduce the one-loop VEV [to order $\mathcal {O}(1/S^4)$]

$$\begin{aligned} \bar{\lambda }= \frac{\kappa ^2\mu ^2 }{2 \alpha _c^2} e^{1+{2\pi ^2}/{\alpha _c^2 S^2}} \sim \frac{\kappa ^2\mu ^2 }{2 \alpha _c^2} e^{1 + {2\pi ^2 \kappa ^2}/{\alpha _c^2 \xi ^2}} . \end{aligned}$$

(19)

In particular, for any value of the dimensionless coupling strength $\alpha _c$, we can choose the renormalization mass scale $\mu$, in such a way that $\bar{\lambda }$ has the value 1, which will guarantee phenomenologically correct gravitational forces at long distances. The VEV $\bar{\lambda }$ is thus the dimensionally transmuted parameter of the massless CG. Its role here is completely analogous to the role of the dimensionally transmuted coupling constant in the Coleman–Weinberg treatment of the massless scalar electrodynamics [69]. Namely, we have traded a dimensionless parameter $\alpha _c$ for a dimensionful parameter $\bar{\lambda }/\kappa ^2$ (which does not exist in the symmetric phase).

By assuming that in the broken phase a cosmologically relevant metric is that of Friedmann–Lamaître–Robertson–Walker (FRLW), then, modulo a topological term, the additional condition

$$\begin{aligned} \int \mathrm{d}^4x (-g)^{1/2} 3R_{\mu \nu }R^{\mu \nu } = \int \mathrm{d}^4x (-g)^{1/2} R^2 , \end{aligned}$$

(20)

holds due to a conformal flatness of the FRLW metric [70]. Combining (9), (19), and (20), the low-energy limit of $\mathcal{A}_\mathrm{conf}$ in the broken phase reads

$$\begin{aligned} \mathcal{A}_\mathrm{conf.b.} = - \frac{1}{2\kappa ^2}\int \mathrm{d}^4x\, (-g)^{1/2} (R - \xi ^2 R^2 - 2{\varLambda }) , \end{aligned}$$

(21)

with

$$\begin{aligned} \xi ^2 = \frac{\kappa ^2S^2}{6\alpha _c^2} ,\quad \varLambda = \frac{3 \alpha _c^2}{4S^2\kappa ^2} . \end{aligned}$$

(22)

We stress that our $\varLambda$ is entirely of a geometric origin (it originates from the CG) and it enters in (21) with the opposite sign in comparison with the usual matter-sector induced (de Sitter) cosmological constant. Note the non-trivial relation between $\xi$ and $\varLambda$, namely $\varLambda = 1/(8\xi ^2)$.

5 Gradient term for $\lambda$

The local conformal symmetry dictates that the scalar degree of freedom must decouple from the on-shell spectrum of the CG [26, 32], whereas in theories without conformal invariance (but with the same tensorial content) the scalar field does appear in the spectrum [12, 32, 37]. When the conformal symmetry is broken the scalar field reappears through a radiatively induced gradient term of the spurion field $\lambda$.

The explicit form of the kinetic term (namely its overall sign!) can be decided from the momentum-dependent part of the $\lambda$ self-energy $\Sigma _{\lambda }$. This can be streamlined by considering in (10) a slowly fluctuating $\lambda$ instead of fixed $\bar{\lambda }$. Since the lowest-order contribution to $\Sigma _{\lambda }$ comes from coupling to $\bar{h}$, the only relevant substitutions in (10) are $\bar{\lambda } \square \bar{h} \mapsto \lambda \square \bar{h}$ (which stops to be a total derivative) and $\bar{h} \bar{\lambda } \square \bar{h} \mapsto {\lambda } {h}^{\mu \nu } 3 P^{(0)}_{\mu \nu , \alpha \beta }\square {h^{\alpha \beta }}= \pi _{\mu \nu }(\lambda {h}^{\mu \nu })\square \bar{h}$ ($P^{(0)}_{\mu \nu , \alpha \beta } = \pi _{\mu \nu }\pi _{\alpha \beta }/3$, which is the spin-0 projection, and $\pi _{\mu \nu } = \eta _{\mu \nu } -\partial _{\mu }\square ^{-1} \partial _{\nu }$, which is the transverse vector projection). In the leading $\alpha _c$-order, one can neglect $\alpha _c^2 \partial _{\mu } \lambda$ with respect to $\alpha _c \partial _{\mu } \lambda$ and complete the square in (10) as follows:

$$\begin{aligned}&- \frac{\alpha _c\lambda }{2\kappa ^2}\square \bar{h} + \bar{h} \mathfrak {C} \square ^2 \bar{h} \nonumber \\&\quad \mapsto \ \bar{h} \mathfrak {C} \square ^2 \bar{h} - \frac{\alpha ^2_c}{16\kappa ^4} \square \lambda (\square ^{-2}\mathfrak {C}^{-1} )\square \lambda \nonumber \\&\quad \approx \bar{h} \mathfrak {C} \square ^2 \bar{h} + \frac{1}{2\kappa ^2\bar{\lambda }} \lambda \square \lambda . \end{aligned}$$

(23)

The last approximation holds for $1 \ll \alpha _c^2\square ^{-1}/(C\kappa )^2 \sim \square ^{-1}/\xi ^2 \sim 10^{28} \square ^{-1}$, and thus in the large-scale cosmology where only low-frequency modes of scalar fields (e.g., $\lambda$) are observationally relevant. The square completion procedure employed in (23) changes the (conformal) gauge fixing condition, albeit the only effect of this modification is a redefinition of the function $\zeta$.

Because of a minus sign in front of $\mathcal{A}_\mathrm{conf}$ in (10), the actual kinetic term is $-\frac{1}{2\kappa ^2\bar{\lambda }} \lambda \square \lambda \sim \frac{1}{2\kappa ^2\bar{\lambda }} \partial _{\mu } \lambda \partial ^{\mu } \lambda$, which is positive. As a result, $\lambda$ morphs into a genuine (non-ghost, non-tachyonic) propagating scalar mode.

In passing, we note that since $V_\mathrm{eff}$ in the broken phase is bounded from below and the kinetic energy is positive (i.e., vacuum decay is prevented), the broken one-loop linearized CG does not possess ghost states.

6 Cosmological implications

Recent polarization data from Planck and WMAP satellites [53, 54] support inflationary models with small tensor-to-scalar ratio: $r < 0.12$ at 95 % CL. These include, e.g., the Starobinsky model (6), the non-minimally coupled model ($\propto \phi ^2 R/2$) with a $V(\phi )\propto \phi ^4/4$-potential, and an inflation model based on a Higgs field [53, 54].

In the SM the linear Einstein term determines the long-wavelength behavior, while the $R^2$-term dominates short distances and drives inflation.

In phenomenological cosmology, the SM represents metric gravity with a curvature-driven inflation. In particular, it does not contain any fundamental scalar field that could be an inflaton, even though a scalar field/inflaton formally appears when transforming the SM to the Einstein frame [71].

SM emerges naturally in CG in the weak-field sector of the broken phase, where the action ${\mathcal {A}}_\mathrm{{conf.b.,\lambda }}$ reads

$$\begin{aligned}&- \frac{1}{2\kappa ^2}\int \mathrm{d}^4x\, (-g)^{1/2} \left( \lambda R - \xi ^2 R^2 - \frac{(\partial _{\mu } \lambda )^2}{\bar{\lambda }} - 2\varLambda \lambda ^2\right) \nonumber \\&\quad \mathop {\longrightarrow }\limits ^{\lambda \rightarrow \bar{\lambda }= 1 } - \frac{1}{2\kappa ^2}\int \mathrm{d}^4x\, (-g)^{1/2} (R - \xi ^2 R^2 - 2\varLambda ) . \end{aligned}$$

(24)

Similarly, as in the usual SM, one can set up for ${\mathcal {A}}_\mathrm{{conf.b.,\lambda }}$ a dual description in terms of a non-minimally coupled auxiliary scalar field $\phi$ with the action [8, 71],

$$\begin{aligned} {\mathcal {A}}_{\phi ,J}= & {} - \frac{1}{\kappa ^2}\int \mathrm{d}^4 x (-g)^{1/2}\left( \frac{\lambda + 2\xi \phi }{2} R + \frac{\phi ^2}{2} \right. \nonumber \\&\left. - \frac{(\partial _{\mu } \lambda )^2}{2\bar{\lambda }} - \varLambda \lambda ^2\right) . \end{aligned}$$

(25)

This is a HS-transformed ${\mathcal {A}}_\mathrm{{conf.b.,\lambda }}$ with $\phi$ being the HS field. To analyze (25) we choose to switch from the Jordan frame (25) to the Einstein frame [8, 72]⁶ where the curvature R enters without a non-minimally coupled fields $\lambda$ and $\phi$. This is obtained via rescaling: $g_{\mu \nu }\ \mapsto (\lambda + 2\xi {\phi })^{-1}g_{\mu \nu }$, giving

$$\begin{aligned} {\mathcal {A}}_{\phi ,E}= & {} - \frac{1}{\kappa ^2}\int \mathrm{d}^4 x (-g)^{1/2}\left[ \frac{\tilde{R}}{2} - \frac{3\xi ^2 (\partial _{\mu }\phi )^2 }{(\lambda +2\xi \phi )^2} \right. \nonumber \\&-\frac{3\xi (\partial _{\mu }\phi ) (\partial ^{\mu }\lambda )}{(\lambda +2\xi \phi )^2} - \frac{(\partial _{\mu }\lambda )^2 }{2\bar{\lambda }(\lambda +2\xi \phi )} - \frac{3 (\partial _{\mu }\lambda )^2}{4(\lambda +2\xi \phi )^2} \nonumber \\&\left. + \frac{\phi ^2}{2(\lambda +2\xi \phi )^2} - \frac{\varLambda \lambda ^2 }{(\lambda +2\xi \phi )^2}\right] . \end{aligned}$$

(26)

The above metric rescaling is valid only for the metric-signature-preserving transformation, i.e., only when $(\lambda + 2\xi {\phi })>0$. The action (26) can be brought into a diagonal form if we pass from fields $\{\lambda , \phi \}$ to $\{\lambda , \psi \}$ where the new field $\psi$ is obtained via the redefinition $\phi = [\exp (\sqrt{2/3} |\psi |) -\lambda ]/(2\xi )$. In terms of $\psi$ the action reads

$$\begin{aligned} {\mathcal {A}}_{\psi , E}= & {} - \frac{1}{\kappa ^2}\int \mathrm{d}^4 x (-g)^{1/2}\left[ \frac{\tilde{R}}{2} - \frac{1}{2}(\partial _{\mu }\psi )^2 + U(\psi ,\lambda ) \right. \nonumber \\&\left. -e^{-\sqrt{2/3}|\psi |} \frac{(\partial _{\mu }\lambda )^2}{2\bar{\lambda }}{}\right] , \end{aligned}$$

(27)

where $U(\psi ,\lambda ) = \frac{1}{8\xi ^2}\left( 1- 2\lambda e^{-\sqrt{2/3}|\psi |}\right)$, with $\xi$ from (22). The strength of $\lambda$-field oscillations is controlled by the size of a coefficient in front of the $\lambda$-gradient term [67], i.e., $e^{-\sqrt{2/3}|\psi |}/\kappa ^2$ (more precisely, the local fluctuations square width $\langle (\lambda (x) - \bar{\lambda })\rangle ^2 \sim \kappa ^2 e^{\sqrt{2/3}|\psi (x)|}$).

At large values of the dimensionless scalar field $\psi$, i.e., at values of the dimensionful field $\tilde{\psi } = \psi /\kappa$ that are large compared to the Planck scale, the gradient coefficient is very small and the $\lambda$-field severely fluctuates. Assuming that CG was broken before the onset of inflation, after a brief period of violent oscillations the $\lambda$-fluctuations are strongly damped ⁷ at $\tilde{\psi } \lesssim 10 m_p$. From then on, the $\lambda$-field settles at its potential minimum at $\bar{\lambda } =1$.

Note that $U(\psi ,\bar{\lambda })\le 1/(8\xi ^2) \ll m_p^2$, which is a necessary condition for a successful inflation. At values of $\tilde{\psi } \sim 10 m_p$, the potential $U(\psi ,\bar{\lambda })$ is sufficiently flat to produce the phenomenologically acceptable slow-roll inflation, with the (collective) scalar field $\psi$ playing the role of the inflaton.

Using the slow-roll parameters

$$\begin{aligned}&\epsilon = \frac{1}{2}m_p^2 \left( \frac{\partial _{\psi }U(\psi ,\bar{\lambda })}{U(\psi ,\bar{\lambda })} \right) ^2, \quad \eta \ = \ m_p^2 \frac{\partial ^2_{\psi }U(\psi ,\bar{\lambda })}{U(\psi ,\bar{\lambda })} , \end{aligned}$$

(28)

($\partial _{\psi } \equiv \partial /\partial \psi$) one can write down the tensor-to-scalar ratio r and the spectral index $n_s$ in the slow-role approximation as [53, 54]

$$\begin{aligned} r = 16 \epsilon , \quad n_s = 1- 6\epsilon + 2\eta . \end{aligned}$$

(29)

In terms of the number N of e-folds left to the end of inflation

$$\begin{aligned} N = - \kappa ^2 \int _{\psi }^{\psi _f} \mathrm{d}\psi \frac{U(\psi ,\bar{\lambda })}{\partial _{\psi }U(\psi ,\bar{\lambda })} \ \approx \ \frac{3}{4\bar{\lambda }} e^{\sqrt{2/3}|\psi |} \end{aligned}$$

(30)

($\psi _{f}$ represents the values of the inflaton at the end of inflation, i.e., when $e^{-\sqrt{2/3}|\psi |}\sim 1$), one gets

$$\begin{aligned}&n_s \approx 1- \frac{2}{N},\quad r \approx \frac{12}{N^2} , \end{aligned}$$

(31)

which for $N = 50 \div 60$ (i.e., values relevant for the CMB) is remarkably consistent with the Planck data [53, 54].

While during the inflation, the $\lambda$-field is constant (due to a large coefficient in front of the gradient term) allowing a large-valued inflaton field to descend slowly from a potential plateau, inflation ends gradually when $\lambda$ regains its canonical kinetic term, and a small-valued inflaton field picks up kinetic energy.

From (27) the dominant interaction channel at small $|\psi |$ is $(\partial _{\mu }\lambda )^2 |\psi |$, hence the vacuum energy density stored in the inflaton field is transferred to the $\lambda$ field via inflaton decay $\psi \rightarrow \lambda + \lambda$ (reheating), possibly preceded by a non-perturbative stage (preheating).

Note also that the gravi-cosmological constant $\varLambda$ that was instrumental in setting the inflaton potential in (27) has the opposite sign when compared with an ordinary (matter-sector induced) cosmological constant. Since the conformal symmetry prohibits the existence of a (scale-full) cosmological constant, the gravi-cosmological constant must correspond to a scale at which the conformal symmetry breaks, which in turn determines the cutoff scale of the scalaron.

The magnitude of $\xi$ in the SM is closely linked to the scale of inflation [8]. Using the values relevant for the CMB with 50–60 e-foldings, the Planck data [53, 54] require $\xi \sim 10^{-13}$ GeV$^{-1}$ or equivalently $\xi /\kappa \sim 10^5$. Thus from (22) the vacuum energy density is $\rho _{\varLambda } \equiv \varLambda /\kappa ^2 \sim 10^{-10}(10^{18} \ \text{ GeV })^4 \sim 2\times 10^{100} \text{ erg }/{\text{ cm }}^3$, which corresponds to a zero-point energy density of a scalaron with an ultraviolet cutoff at $10^{15}$–$10^{16}$ GeV. This is in the range of the GUT inflationary scale. For compatibility with an inflation-induced large structure formation the conformal symmetry should be broken before (or during) inflation.⁸ This can be naturally included in a broader theoretical context of the “conformal inflation” paradigm, which has been the thrust of much of the recent research [74–77]. Let us also notice that the existence of a single scalar field with cutoff at the GUT scale and coupled to broken CG (e.g., $\lambda$ or a GUT Higgs field) would contribute with a positive zero-point energy that could substantially reduce or eliminate $\varLambda$.

7 Conclusions

To conclude, we have shown that a spurion-field mediated spontaneous symmetry breakdown of CG is capable of transforming a purely metric conformal gravity into an effective scalar–tensor gravity.

This offers a new paradigm for understanding inflationary and large-scale cosmology. In particular, we have shown that the low-energy dynamics in the broken phase is described by a Starobinsky-type f(R)-model, which can be mapped on a two-field hybrid inflationary model. A dimensional transmutation ties up the values of Starobinsky’s inflation parameter $\xi$ and the gravi-cosmological constant $\varLambda$. This fixes the symmetry-breakdown scale for CG to be roughly the GUT inflationary scale. Despite its simplicity, the presented paradigm reproduces not only a phenomenologically acceptable picture of the large-scale Universe that is compatible with the present Planck and WMAP data, but it also provides a viable mechanism for the reheating. Last but not least, the negative gravi-cosmological constant could help to reduce the difference between theoretically estimated $\rho _{\varLambda }^{(\mathrm {th})}$ and astronomically observed $\rho _{\varLambda }^{(\mathrm {obs})}$. This would be a particularly powerful scenario when the local conformal symmetry were a true fundamental symmetry above the inflationary scale.⁹

If the original BICEP2 collaboration claimed data supporting inflationary models with a large $r > 0.16$ (i.e., we have a large-field case) were true, then the conventional Starobinsky-type inflationary potential would be excluded. In turn, this would also invalidate the outlined scenario. Fortunately, a recent joint analysis of BICEP2/Keck Array and Planck data indicates that the original Planck conclusions (on which the cosmological part of this paper is based) are still valid. In particular, BICEP2/Keck Array and Planck data still support inflationary models with a small tensor-to-scalar ratio with an upper limit $r < 0.12$ [78].

Appendix A

Here we collect some technical points used in the text. The weak-field expansion of $\mathcal{A}_\mathrm{conf}$ is based on the fluctuating field $h_{\mu \nu }$: $g_{\mu \nu } = \eta _{\mu \nu } + \alpha _c h_{\mu \nu }$. This gives ${R}_{\alpha \beta \lambda \delta } = \frac{\alpha _c}{2} \left[ \partial _\beta \partial _\lambda h_{\alpha \delta } + \partial _\alpha \partial _\delta h_{\beta \lambda } - (\alpha \leftrightarrow \beta )\right]$ and to the order $\alpha _c^2$ results in

$$\begin{aligned} \sqrt{-g}= & {} 1 + \frac{\alpha _c}{2} h^{\mu }_{\mu } + \frac{\alpha _c^2}{8}\left( h^{\mu }_{\mu }h^{\nu }_{\nu } - 2 h_{\mu }^{\nu }h_{\nu }^{\mu } \right) , \nonumber \\ \sqrt{-g} {R}_{\alpha \delta }^2\!= & {} \frac{\alpha _c^2}{4} (\partial _\alpha \partial _\lambda h_{\delta }^{\lambda }\! + \partial _\delta \partial _\lambda h_{\alpha }^{\lambda }\! - \partial _\alpha \partial _\delta h\! - \partial ^2 h_{\alpha \delta })^2\, , \nonumber \\ \sqrt{-g}{R}^2= & {} \alpha _c^2(\partial ^2 h - \partial _\alpha \partial _\beta h^{\alpha \beta })^2 . \end{aligned}$$

(32)

With this the weak-field expansion of the Weyl action, (1) reads (modulo total derivatives) [26]

$$\begin{aligned} \mathcal{A}_\mathrm{conf}= & {} -\frac{1}{8\alpha _c^2}\int \mathrm{d}^4x\, (-g)^{1/2}C_{\lambda \mu \nu \kappa } C^{\lambda \mu \nu \kappa }\nonumber \\= & {} -\frac{1}{16}\int \mathrm{d}^4x\, h^{\mu \nu } P^{(2)}_{\mu \nu , \alpha \beta }\square ^2 h^{\alpha \beta } \nonumber \\= & {} -\frac{1}{16}\int \mathrm{d}^4x\, (\square \bar{h}^{\alpha \beta , \bot })^2 . \end{aligned}$$

(33)

Here, $P^{(2)}_{\mu \nu , \alpha \beta }= \pi _{\mu (\alpha }\pi _{\beta )\nu } -\frac{1}{3} \pi _{\mu \nu }\pi _{\alpha \beta }$ is the spin-2 projection, and $\pi _{\mu \nu } = \eta _{\mu \nu } -\partial _{\mu }\square ^{-1} \partial _{\nu }$ is the transverse vector projection. We also used $\bar{h}^{\alpha \beta , \bot }$, which is defined via two tensor decompositions: (a) $h_{\mu \nu } = \bar{h}_{\mu \nu } + \frac{1}{4}\eta _{\mu \nu }\varphi$ ($\varphi \equiv h^{\alpha }_{\alpha }$ so that $\bar{h}^{\alpha }_{\alpha } = 0$) and (b) $\bar{h}_{\mu \nu } = \bar{h}_{\mu \nu }^{\bot } + \partial _{\mu }\eta ^{\bot }_{\nu } + \partial _{\nu }\eta ^{\bot }_{\mu } + \partial _{\mu }\partial _{\nu } \sigma - \frac{1}{4}\eta _{\mu \nu }\partial ^2 \sigma$ (with $\partial ^{\mu }\bar{h}_{\mu \nu }^{\bot } = 0$ and $\partial ^{\mu }\eta ^{\bot }_{\mu }=0$), which serve to identify irreducible degrees of freedom. Using the conformal gauge [11, 26] $\varphi = 0$ and the coordinate gauge $\partial _{\mu }h^{\mu \nu } = 0$ (with the associated Faddeev–Popov operator $(\mathcal {M}_\mathrm{FP})_{\mu \nu } = -\square \eta _{\mu \nu } - \partial _{\mu } \partial _{\nu }$) the functional measure reads

$$\begin{aligned} {\mathcal {D}}h_{\mu \nu }= & {} {\mathcal {D}} \bar{h}_{\mu \nu }^{\bot }{\mathcal {D}} \eta ^{\bot }_{\mu } {\mathcal {D}} \sigma {\mathcal {D}} \varphi \det (-\square )_{\sigma } [\det (-\eta _{\mu \nu }\square )_{\eta ^{\bot }} ]^{1/2}\nonumber \\\mapsto & {} {\mathcal {D}} \bar{h}_{\mu \nu }^{\bot } [\det (-\square )_{\sigma } \det (-\eta _{\mu \nu }\square )_{\eta ^{\bot }} ]^{1/2}\, . \end{aligned}$$

(34)

For one-loop effective-action calculations we used a more convenient approach, in which the weak-field action $\mathcal{A}_\mathrm{conf}$ is written in terms of the unconstrained variable $h_{\mu \nu }$ as

$$\begin{aligned} -\frac{1}{16}\!\int \mathrm{d}^4x \left[ h^{\mu \nu } \square ^2 h_{\mu \nu } - \partial _{\lambda } h^{\lambda \mu } H_{\mu \nu } \partial _{\rho } h^{\rho \nu } - \frac{1}{6} \bar{h} \square ^2 \bar{h}\right] .\nonumber \\ \end{aligned}$$

(35)

Here $H_{\mu \nu } = 1/2 \partial _{\mu }\partial _{\nu } - \square \eta _{\mu \nu }$ and $\bar{h} = h^{\mu }_{\mu } - \partial _{\mu } \square ^{-1}\partial _{\nu } h^{\mu \nu }$. To obtain the diagonal kinetic operator one has to cancel the second and third therm by fixing the gauges: $\chi ^{\nu } \equiv \partial _{\mu } h^{\mu \nu } = \zeta ^{\nu }(x)$ (coordinate gauge) and $\chi \equiv \bar{h} = \zeta (x)$ (conformal gauge). As before, the Faddeev–Popov operator for the coordinate gauge is $(\mathcal {M}_\mathrm{FP})_{\mu \nu } = -\square \eta _{\mu \nu } - \partial _{\mu } \partial _{\nu }$, while for conformal gauge $(\mathcal {N}_\mathrm{FP}) = (D-1)\delta ^{(D)}(x-y)$. In this case the functional-integral measure is

$$\begin{aligned} {\mathcal {D}}h_{\mu \nu } \mapsto {\mathcal {D}}h_{\mu \nu } \delta [\chi - \zeta ]\delta [\chi ^{\nu } - \zeta ^{\nu }] \det (\mathcal {M}_\mathrm{FP})\, \end{aligned}$$

(36)

($\zeta$ and $\zeta ^{\mu }$ are arbitrary functions of x). With the help of ’t-Hooft’s averaging trick the corresponding partition function coincides with that obtained from (33)–(34).