1 Introduction

Non-locality in modern theoretical physics is certainly a key issue, as there are many hints suggesting that the evolution of quantum mechanical states cannot be properly described without taking into account the extension (in space and time) of the whole physical system under consideration (or, naively, its whole wave-function in position space). Non-locality also appears at the classical level in systems in which gravity plays a crucial role, a remarkable example being given by trapping surfaces and horizons. In fact, the location of a trapping surface can be determined by just considering the metric locally; however, the metric itself at a point will in general depend on all of the matter sources around, and in a complicated non-linear manner. An event horizon can then only be identified provided one knows the entire history of the space-time. In any quantum theory of gravity, it is therefore likely that space and time non-locality will become one of the most prominent features overall.

Unusual causal structures, like the trapping surfaces and horizons, could only occur in strongly gravitating systems, such as astrophysical objects that collapse and possibly form black holes. One might argue that, for a large black hole, gravity should appear “locally weak” at the horizon, since tidal forces look small to a freely falling observer (their magnitude being roughly controlled by the surface gravity which is inversely proportional to the horizon radius). However, light (like any other classical signal) is confined inside the horizon, no matter how weak such local forces may appear to a local observer, which we could take as the definition of a “globally strong” interaction. Moreover, for a small black hole (with a mass about the Planck scale), tidal forces become strong both in the local and global sense, thus granting such an energy scale a remarkable role in the search for a quantum theory of gravity. It is indeed not surprising that modifications to the standard commutators of quantum mechanics and generalised uncertainty principles (GUPs) have been proposed, essentially in order to account for the possible existence of small black holes around the Planck scale, and the ensuing minimum measurable length [1, 2]. Unfortunately, that regime is presently well beyond our experimental capabilities, at least if one takes the Planck scale at face value. Nonetheless, there is the possibility that the low energy theory still retains some signature features that could be accessed in the near future (see, for example, Refs. [3, 4]).

Before we start calculating phenomenological predictions, it is of the foremost importance that we clarify the possible conceptual issues arising from the use of arguments and observables that we know work at our every-day scales. One of such key concepts is the gravitational radius of a self-gravitating source, which can be used in order to asses the existence of trapping surfaces, at least in spherically symmetric systems, whose metric \(g_{\mu \nu }\) can be written asFootnote 1

$$\begin{aligned} {\mathrm{d}}s^2=g_{ij}\,{\mathrm{d}}x^i\,{\mathrm{d}}x^j+r^2(x^i)({\mathrm{d}}\theta ^2+\sin ^2\theta \,{\mathrm{d}}\phi ^2), \end{aligned}$$
(1.1)

where \(r\) is the areal coordinate and \(x^i=(x^1,x^2)\) are coordinates on surfaces of constant angles \(\theta \) and \(\phi \). The location of a trapping surface is then determined by the equation

$$\begin{aligned} g^{ij}\,\nabla _i r\,\nabla _j r=0, \end{aligned}$$
(1.2)

where \(\nabla _i r\) is perpendicular to surfaces of constant area \(\mathcal {A}=4\,\pi \,r^2\). If we set \(x^1=t\) and \(x^2=r\) and denote the matter density as \(\rho =\rho (r,t)\), the Einstein field equations tell us that

$$\begin{aligned} g^{rr}=1-\frac{2\,\ell _{\mathrm{p}}\,(m/m_{\mathrm{p}})}{r}, \end{aligned}$$
(1.3)

where the Misner–Sharp mass is given by

$$\begin{aligned} m(r,t)=4\,\pi \int _0^r \rho (\bar{r},t)\,\bar{r}^2\,{\mathrm{d}}\bar{r}, \end{aligned}$$
(1.4)

as if the space inside the sphere were flat. A trapping surface then exists if there are values of \(r\) (and \(t\)) such that the gravitational radius,

$$\begin{aligned} R_{\mathrm{H}}=2\,\ell _{\mathrm{p}}\,\frac{m}{m_{\mathrm{p}}}, \end{aligned}$$
(1.5)

satisfies

$$\begin{aligned} R_{\mathrm{H}}(r,t)\ge r. \end{aligned}$$
(1.6)

If the above relation holds in the vacuum outside the region where the source is located, \(R_{\mathrm{H}}\) becomes the usual Schwarzschild radius, and the above argument gives a mathematical foundation to Thorne’s hoop conjecture [5], which (roughly) states that a black hole forms when the impact parameter \(b\) of two colliding small objects is shorter than the Schwarzschild radius of the system, that is, for \(b \lesssim 2\,\ell _{\mathrm{p}}\,{E}/{m_{\mathrm{p}}}\), where \(E\) is the total energy in the centre-of-mass frame.

The above treatment becomes questionable for sources of the Planck size or lighter, for which we know for an experimental fact that quantum effects may not be neglected. Consider in fact a spin-less point-like particle of mass \(m\), whose Schwarzschild radius is given by \(R_{\mathrm{H}}\) in Eq. (1.5) with \(m\) now a constant. The Heisenberg principle of quantum mechanics introduces an uncertainty in the particle’s spatial localisation of the order of the Compton–de Broglie length, \(\lambda _m \simeq \ell _{\mathrm{p}}\,{m_{\mathrm{p}}}/{m}\). Since quantum physics is a more refined description of reality, we could argue that \(R_{\mathrm{H}}\) only makes sense ifFootnote 2

$$\begin{aligned} R_{\mathrm{H}}\gtrsim \lambda _m\quad \Rightarrow \quad m\gtrsim m_{\mathrm{p}}, \end{aligned}$$
(1.7)

which brings us to face a conceptual challenge: how can we describe quantum mechanical systems (like the elementary particles) which are classically expected to have a horizon smaller than the size of the uncertainty in their position?

In Refs. [6, 7], a proposal was put forward in order to describe the “fuzzy” Schwarzschild (or gravitational) radius of a localised (but likewise fuzzy) quantum source, which was then shown to induce a GUP and minimum measurable length [8], and also yields corrections to the classical hoop conjecture [9]. The same approach shows that Bose–Einstein condensate (BEC) models of black holes [10–17] actually possess a horizon, with a proper semiclassical limit [19]. It is important to emphasise that our approach differs from most previous attempts in which the gravitational degrees of freedom of the horizon, or of the black hole metric, are quantised independently of the nature and state of the source (for some bibliography, see, e.g., Ref. [18]). In our case, the gravitational radius is instead quantised along with the matter source that produces it, somewhat more in line with the highly non-linear general relativistic description of the gravitational interaction. However, having given a practical tool for describing the gravitational radius of a generic quantum system is just the starting point. In fact, when the probability that the source is localised within its gravitational radius is significant, the system should show (some of) the properties ascribed to a black hole in general relativity. These properties, the fact in particular that no signal can escape from the interior, only become relevant once we consider how the overall system evolves. In this work, we shall hence address the crucial issue of the time evolution of quantum states with a “fuzzy” horizon.

In the next section, we shall first review the general idea of the horizon wave-function, and then analyse in detail the case of a massive spherical particle at rest. In Sect. 3, the spherical particle will serve as a toy model to investigate a proposal for a modified, causal evolution, in which the possible presence of a horizon is taken into account. We shall finally comment on our results and some of the limitations of our approach in Sect. 4.

2 Static horizon wave-function

Let us start by reviewing the wave-function for the gravitational radius that can be associated with any localised quantum mechanical particle [6, 7]. As we mentioned in the Introduction, this wave-function emerges from relating the matter source to its gravitational radius at the quantum level, rather than considering quantum gravitational degrees of freedom independently [18], and it allows us to put on more quantitative grounds the condition (1.7), which should distinguish black holes from regular particles.

2.1 Formal definitions

For the sake of clarity, we shall just consider quantum mechanical states representing spherically symmetric sources which are both localised in space and at rest in the chosen reference frame. In fact, localisation is an essential ingredient for generating trapping surfaces and black holes, and we wish to avoid the complications due to the relative motion of the source and departure from sphericity. We shall also ignore any possible time evolution for now. Our “particle-like” state will consequently be described by a wave-function \({\psi }_{\mathrm{S}}\in L^2(\mathbb {R}^3)\), which can be decomposed into energy eigenstates,

$$\begin{aligned} {\vert {\psi }_{\mathrm{S}}\rangle }=\sum _E\,C(E)\,{\vert \psi _E\rangle },\end{aligned}$$
(2.1)

where the sum represents the spectral decomposition in the Hamiltonian eigenmodes,

$$\begin{aligned} \hat{H}\,{\vert \psi _E\rangle }=E\,{\vert \psi _E\rangle }, \end{aligned}$$
(2.2)

and \(H\) should be specified depending on the system we wish to consider.

We can now try and quantise the gravitational radius determined by the Misner–Sharp mass (1.4), by simply expressing the energy in terms of the Schwarzschild radius, \(E=m_{\mathrm{p}}\,{r_{\mathrm{H}}}/{2\,\ell _{\mathrm{p}}}\), and define the horizon wave-function

$$\begin{aligned} {\psi }_{\mathrm{H}}(r_{\mathrm{H}})={\mathcal {N}_{\mathrm{H}}}\,C(r_{\mathrm{H}}(E)), \end{aligned}$$
(2.3)

whose normalisation \(\mathcal {N}_{\mathrm{H}}\) can be fixed by using the norm defined by the scalar product

$$\begin{aligned} {\langle {\psi }_{\mathrm{H}} \mid \phi _{\mathrm{H}} \rangle }=4\,\pi \int _0^\infty {\psi }_{\mathrm{H}}^*(r_{\mathrm{H}})\,\phi _{\mathrm{H}}(r_{\mathrm{H}})\,r_{\mathrm{H}}^2\,{\mathrm{d}}r_{\mathrm{H}}. \end{aligned}$$
(2.4)

Let us remark again that this quantum description of the gravitational radius can be viewed as a particular way of quantising the Einstein equation (1.3), which lifts to the quantum level the relation between \(R_{\mathrm{H}}\) and the Misner–Sharp mass \(m\) determined by the matter source according to Eq. (1.4). In other words, we are assuming that the only relevant quantum degrees of freedom associated with the gravitational structure of space-time (which classically give rise to trapping surfaces) are those determined by the quantum degrees of freedom of the matter source. This implies that, at least in the static case, we can just consider “on-shell” states for the gravitational degrees of freedom [the “mass-shell” relation being here precisely Eq. (1.3) viewed as an operator equation], and we can neglect the contribution of “purely gravitational” fluctuations. The latter could then be studied by employing standard background field method techniques, in the same way one determines the Lamb shift for the hydrogen atom.

We can interpret the normalised wave-function \({\psi }_{\mathrm{H}}\) as yielding the probability that we would detect a gravitational radius of areal radius \(r=r_{\mathrm{H}}\) associated with the particle in the quantum state \({\psi }_{\mathrm{S}}\). Such a radius is necessarily “fuzzy”, like the energy and the position of the particle itself, and it will have an uncertainty

$$\begin{aligned} \Delta r_{\mathrm{H}}=\sqrt{{\langle r_{\mathrm{H}}^2 \rangle }-{\langle r_{\mathrm{H}} \rangle }^2}. \end{aligned}$$
(2.5)

Moreover, having defined the \({\psi }_{\mathrm{H}}\) associated with a given \({\psi }_{\mathrm{S}}\), we can also define the conditional probability density that the particle lies inside its own gravitational radius \(r_{\mathrm{H}}\) as

$$\begin{aligned} \mathcal {P}_<(r<r_{\mathrm{H}})=P_{\mathrm{S}}(r<r_{\mathrm{H}})\,\mathcal {P}_{\mathrm{H}}(r_{\mathrm{H}}), \end{aligned}$$
(2.6)

where

$$\begin{aligned} P_{\mathrm{S}}(r<r_{\mathrm{H}})=4\,\pi \,\int _0^{r_{\mathrm{H}}}|{\psi }_{\mathrm{S}}(r)|^2\,r^2\,{\mathrm{d}}r \end{aligned}$$
(2.7)

is the usual probability that the particle is found inside a sphere of radius \(r=r_{\mathrm{H}}\), and

$$\begin{aligned} \mathcal {P}_{\mathrm{H}}(r_{\mathrm{H}})=4\,\pi \,r_{\mathrm{H}}^2\,|{\psi }_{\mathrm{H}}(r_{\mathrm{H}})|^2 \end{aligned}$$
(2.8)

is the probability density that the gravitational radius is located on the sphere of radius \(r=r_{\mathrm{H}}\). Since this is the analogue of the condition (1.6), one can also view \(\mathcal {P}_<(r<r_{\mathrm{H}})\) as the probability density that the sphere \(r=r_{\mathrm{H}}\) is a trapping surface. Finally, the probability that the particle described by the wave-function \({\psi }_{\mathrm{S}}\) is a black hole (regardless of the horizon size) will be obtained by integrating (2.6) over all possible values of \(r_{\mathrm{H}}\), namely

$$\begin{aligned} P_{\mathrm{BH}}=\int _0^\infty \mathcal {P}_<(r<r_{\mathrm{H}})\,{\mathrm{d}}r_{\mathrm{H}}, \end{aligned}$$
(2.9)

which will depend on the observables and parameters of the specific state \({\psi }_{\mathrm{S}}\) we started the construction. Let us again emphasise that we have frozen any possible time dependence so far, or, equivalently, the above quantities are only defined at a given instant of time.

2.2 Single massive particle

As the simplest example, we shall consider a massive particle at rest described by the Gaussian wave-function [6–8]

$$\begin{aligned} {\psi }_{\mathrm{S}}(r)=\frac{e^{-\frac{r^2}{2\,\ell ^2}}}{\ell ^{3/2}\,\pi ^{3/4}}. \end{aligned}$$
(2.10)

From the usual flat-space normal modes

$$\begin{aligned} j_0(p\,r)=\frac{\sin (p\,r)}{\sqrt{2^3\,\pi ^3}\,p\,r}, \end{aligned}$$
(2.11)

one obtains the momentum space wave-function

$$\begin{aligned} {\psi }_{\mathrm{S}}(p)\equiv 4\,\pi \,\int _0^\infty {\psi }_{\mathrm{S}}(r)\,j_0(p\,r)\,r^2\,{\mathrm{d}}r=\frac{e^{-\frac{p^2}{2\,\Delta ^2}}}{\Delta ^{3/2}\,\pi ^{3/4}},\nonumber \\ \end{aligned}$$
(2.12)

where \(p^2=\vec p\cdot \vec p\) and \(\Delta =m_{\mathrm{p}}\,\ell _{\mathrm{p}}/\ell \). For the energy of the particle, in accord with the above choice of modes, we simply assume the relativistic mass-shell relation in flat space,

$$\begin{aligned} E^2=p^2+m^2\ge m^2, \end{aligned}$$
(2.13)

and we treat \(\lambda _m \simeq \ell _{\mathrm{p}}\,{m_{\mathrm{p}}}/{m}\) and \(\ell \) as two independent length scales, although it is reasonable to assume that

$$\begin{aligned} \ell \gtrsim \lambda _m, \end{aligned}$$
(2.14)

since one does not expect it is physically possible to locate a particle with an accuracy greater than its Compton length. Upon expressing \(E\) in terms of the Schwarzschild radius, \(E=m_{\mathrm{p}}\,{r_{\mathrm{H}}}/{2\,\ell _{\mathrm{p}}}\), we obtain the horizon wave-function

$$\begin{aligned} {\psi }_{\mathrm{H}}(r_{\mathrm{H}})\simeq \Theta (r_{\mathrm{H}}-r_{\mathrm{m}})\,\exp \left[ -\frac{\ell ^2}{8\,\ell _{\mathrm{p}}^4}\,(r_{\mathrm{H}}^2-r_{m}^2)\right] , \end{aligned}$$
(2.15)

where

$$\begin{aligned} r_{m}=2\,\ell _{\mathrm{p}}\,\frac{m}{m_{\mathrm{p}}} \end{aligned}$$
(2.16)

is the minimum allowed value of \(r_{\mathrm{H}}\) corresponding to the minimum value of \(E=m\), and \(\Theta \) is Heaviside’s step function. The normalisation of \({\psi }_{\mathrm{H}}\) should then be fixed in the scalar product (2.4). Since for the minimum width \(\ell \simeq \lambda _m\), one has \({\langle r_{\mathrm{H}} \rangle }\simeq \ell _{\mathrm{p}}^2/\ell \simeq R_{\mathrm{H}}\) and

$$\begin{aligned} \Delta r_{\mathrm{H}}=\sqrt{{\langle r_{\mathrm{H}}^2 \rangle }-{\langle r_{\mathrm{H}} \rangle }^2}\simeq {\ell _{\mathrm{p}}^2}/{\ell }. \end{aligned}$$
(2.17)

One finds the uncertainty \(\Delta r_{\mathrm{H}}\simeq R_{\mathrm{H}}\), which is dangerously large for a macroscopic black hole with \(R_{\mathrm{H}}\gg \ell _{\mathrm{p}}\). In fact, this result could be viewed as supporting the picture that macroscopic black holes should be made of a very large number \(N\) of very light particles, precisely like the BEC of gravitons of Refs. [10–17], for which one instead obtains \(\Delta r_{\mathrm{H}}/{\langle r_{\mathrm{H}} \rangle }\sim 1/N\) [19].

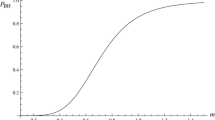
From \({\psi }_{\mathrm{S}}\) in Eq. (2.10) and the normalised \({\psi }_{\mathrm{H}}\) from Eq. (2.15), one can numerically obtain the probability \(P_{\mathrm{BH}}=P_{\mathrm{BH}}(\ell ;m)\), which is plotted in the left panel of Fig. 1, for a few values of \(m\) about and below the Planck scale, and \(\ell \ge \lambda _m\). On considering the limiting case \(\ell =\lambda _m\), one obtains \(P_{\mathrm{BH}}=P_{\mathrm{BH}}(\ell )\) displayed by the dots in the right panel of Fig. 1. It is then interesting to notice that these points are fairly well approximated by the analytical expression used in Refs. [6–8]. By formally taking the limit \(r_{m}\rightarrow 0\) in Eq. (2.15) and normalising according to Eq. (2.4), one obtains

$$\begin{aligned} {\psi }_{\mathrm{H}}(r_{\mathrm{H}})=\frac{\ell ^{3/2}\,e^{-\frac{\ell ^2\,r_{\mathrm{H}}^2}{8\,\ell _{\mathrm{p}}^4}}}{2\,\sqrt{2}\,\ell _{\mathrm{p}}^{3/2}\,\pi ^{3/4}}, \end{aligned}$$
(2.18)

which then leads to

$$\begin{aligned} P_{\mathrm{BH}}(\ell )=\frac{2}{\pi }\left[ \arctan \left( 2\,\frac{\ell _{\mathrm{p}}^2}{\ell ^2}\right) -\frac{2\,\ell ^2\,(\ell ^4/\ell _{\mathrm{p}}^4-4)}{\ell _{\mathrm{p}}^2\,(4+\ell ^4/\ell _{\mathrm{p}}^4)}\right] . \end{aligned}$$
(2.19)

This probability is represented by the solid line in the right panel of Fig. 1, where one can see that it only underestimates the correct probability for values of \(m\gtrsim m_{\mathrm{p}}/2\) (that is, \(\ell \lesssim 2\,\ell _{\mathrm{p}}\)).

Fig. 1
figure 1

Left panel probability that a particle of Gaussian width \(\ell \ge \lambda _m\) is a black hole for mass \(m=m_{\mathrm{p}}\) (solid line), \(m=3\,m_{\mathrm{p}}/4\) (dashed line) and \(m=m_{\mathrm{p}}/2\) (dotted line). Right panel probability that a particle of Gaussian width \(\ell =\lambda _m\) is a black hole (dots) compared to its analytical approximation (2.19)

Full size image

3 Causal time evolution

Let us now try and investigate the time evolution of the simple toy model of a spherically symmetric particle described above. In order to disentangle the effects on the dynamics due to the horizon from other physics, we shall neglect any non-gravitational interaction, and assume that the UV completion of gravity at the Planck scale does not introduce any new mechanisms.Footnote 3

From the point of view of an observer located sufficiently far from the particle, we can assume we have reliable knowledge of two limiting cases:

  1. (a)

    if the particle is not a black hole (\(P_{\mathrm{BH}}\ll 1\)), the evolution occurs according to the usual laws of quantum mechanics. For the free massive particle described by the Gaussian packet (2.10), this means free evolution according to the Hamiltonian \(H=E\) in Eq. (2.13);

  2. (b)

    if the system is a black hole (\(P_{\mathrm{BH}}\simeq 1\)), no evolution appears to occur at all. Note we are specifically neglecting Hawking evaporation in this simplified hypothesis, and we view a black hole like a “frozen star”.Footnote 4

When the particle is in a generic quantum state \({\psi }_{\mathrm{S}}\) not satisfying any of the above two limiting conditions, we then assume that the evolution for “short” time intervals \(\delta t\) is ruled by the simple prescription

$$\begin{aligned} {\psi }_{\mathrm{S}}(r,t+\delta t)=\left[ \mu _{\mathrm{H}}(t)\,\hat{\mathbb {I}}+\bar{\mu }_{\mathrm{H}}(t)\,e^{-\frac{i}{\hbar }\,\hat{H}\,\delta t}\right] {\psi }_{\mathrm{S}}(r,t), \end{aligned}$$
(3.1)

where \(\hat{\mathbb {I}}\) is the identity operator, \(\mu _{\mathrm{H}}(t)\simeq P_{\mathrm{BH}}(t)\) and \(\bar{\mu }_{\mathrm{H}}(t)\simeq 1-P_{\mathrm{BH}}(t)\), so that the two limiting behaviours (a) and (b) are both accounted for by construction. In fact, we first note that, upon assuming that \(\mu _{\mathrm{H}}\) and \(\bar{\mu }_{\mathrm{H}}\) are real, unitarity is preserved provided these coefficients satisfy the normalisation condition

$$\begin{aligned} 1= & {} \mu _{\mathrm{H}}^2+\bar{\mu }_{\mathrm{H}}^2+2\,\bar{\mu }_{\mathrm{H}}\,\mu _{\mathrm{H}}\,\cos \left( (\delta t/\hbar )\,\hat{H}\right) \nonumber \\= & {} \left( \mu _{\mathrm{H}}+\bar{\mu }_{\mathrm{H}}\right) ^2+\mathcal {O}(\delta t^2), \end{aligned}$$
(3.2)

or \(\bar{\mu }_{\mathrm{H}}\simeq 1-\mu _{\mathrm{H}}\). The evolution equation then becomes

$$\begin{aligned} i\,\hbar \,\frac{\delta {\psi }_{\mathrm{S}}(r,t)}{\delta t}\simeq \left[ 1-P_{\mathrm{BH}}(t)\right] \hat{H}\,{\psi }_{\mathrm{S}}(r,t), \end{aligned}$$
(3.3)

which has the form of an effective Schrödinger equation, and the standard quantum mechanical evolution is exactly recovered in the limit \(P_{\mathrm{BH}}\rightarrow 0\) [limiting case (a)]. Note, however, that \(P_{\mathrm{BH}}=P_{\mathrm{BH}}(t)\) depends on the whole wave-function \({\psi }_{\mathrm{S}}={\psi }_{\mathrm{S}}(r,t)\) and the apparently trivial correction it entails is actually highly non-local, in the sense that it cannot be straightforwardly reproduced by an interacting term of the form \(H_{\mathrm{int}}=H_{\mathrm{int}}(r,t)\).

This observation makes it clear that it will in general be very difficult to solve Eq. (3.3) for a finite time interval. It is instead easier to stick with Eq. (3.1), and employ the spectral decomposition at time \(t\),

$$\begin{aligned} {\psi }_{\mathrm{S}}(r,t)=\sum _EC_E(t)\,j_0(E,r), \end{aligned}$$
(3.4)

which then leads to

$$\begin{aligned} i\,\hbar \,\delta C_E(t)\simeq \left[ 1-P_{\mathrm{BH}}(t)\right] E\,C_E(t)\,{\delta t}, \end{aligned}$$
(3.5)

where we recall the time-dependent coefficient \(P_{\mathrm{BH}}=P_{\mathrm{BH}}(t)\) is determined by the whole wave-function \({\psi }_{\mathrm{S}}={\psi }_{\mathrm{S}}(r,t)\). From Eq. (3.5), and knowing \({\psi }_{\mathrm{S}}\) at the time \(t\), one can reconstruct both \({\psi }_{\mathrm{S}}\) and \({\psi }_{\mathrm{H}}\) at \(t+\delta t\). These two wave-functions will then allow one to proceed to the next time step. We also notice that the approximation (3.2) requires

$$\begin{aligned} \delta t\lesssim \frac{\hbar }{E}=\ell _{\mathrm{p}}\,\frac{m_{\mathrm{p}}}{E}, \end{aligned}$$
(3.6)

which shall be duly commented on, and properly taken into account, in the following.

3.1 Short time evolution

The above evolution equations can be applied to the Gaussian wave-function (2.10), for which the initial probability \(P_{\mathrm{BH}}(t=0)=P_{\mathrm{BH}}(\ell ;m)\) was computed numerically in the previous section. From that result, we expect the particle will likely be a black hole only if \(m\gtrsim m_{\mathrm{p}}\) and \(\ell \lesssim \ell _{\mathrm{p}}\).

In particular, according to Eq. (3.6) with \(m\simeq m_{\mathrm{p}}\), we expect our evolution equation (3.5) holds for

$$\begin{aligned} \delta t\lesssim \hbar /E\simeq \ell _{\mathrm{p}}, \end{aligned}$$
(3.7)

and shorter for modes with energy \(E>m_{\mathrm{p}}\). One might question the validity of our approach for trans-Planckian modes, and such sub-Planckian times. First of all, it is interesting to note that the duality \((E>m_{\mathrm{p}})\Leftrightarrow (\delta t<\ell _{\mathrm{p}})\) clearly appears in this dynamics. Further, we have already commented that the evolution equation (3.1) could only hold in the (admittedly unrealistic approximation) that non-gravitational forces can be neglected and the UV completion of gravity is trivial. Different cases could be considered by modifying the dispersion relation (2.13), but we shall see that our very strong simplifications nonetheless allow us to draw some interesting (qualitative) conclusions.

We now proceed to solve Eq. (3.5) with the time step (3.7), and we then invert the spectral decomposition (3.4) in order to reconstruct the wave-function \({\psi }_{\mathrm{S}}\) at the time \(t=\delta t\). This procedure can be carried out analytically, provided the probability \(P_{\mathrm{BH}}(\ell ;m)\) is given, but the result is better described graphically. In Fig. 2, we plot the probability density \({\mathcal P}_{\mathrm{S}}=4\,\pi \,r^2\,|{\psi }_{\mathrm{S}}(r,t)|^2\) at \(t=0\) and \(t=\delta t=\ell _{\mathrm{p}}\) obtained from the modified evolution (3.3), for a value of the mass of \(m=3\,m_{\mathrm{p}}/4\) and \(\ell =\lambda _m=4\,\ell _{\mathrm{p}}/3\), and we confront it with the probability density obtained from the standard free evolution at the same time \(t=\ell _{\mathrm{p}}\). This case corresponds to a minimum gravitational radius \(r_m=1.5\,\ell _{\mathrm{p}}\), an expectation vale of the energy \({\langle E \rangle }\simeq 1.15\,m_{\mathrm{p}}\), a Schwarzschild radius \(R_{\mathrm{H}}={\langle \hat{r}_{\mathrm{H}} \rangle }\simeq 2.3\,\ell _{\mathrm{p}}\), and initial probability \(P_{\mathrm{BH}}\simeq 0.8\). The time step \(\delta t=\ell _{\mathrm{p}}\) saturates (and likely exceeds) the allowed bound, but was chosen in order to make it clear that the packet remains more confined than one would expect according to the usual quantum mechanical evolution. Since the packet still spreads, one expects the probability \(P_{\mathrm{BH}}(t+\delta t)<P_{\mathrm{BH}}(t)\), and the effect of the horizon will weaken over time. In order to support this expectation, we need to be able to study the time evolution over more than one time step.

Fig. 2
figure 2

Time evolution of the probability density for the initial Gaussian packet (2.10) with \(m=3\,m_{\mathrm{p}}/4\) and \(\ell =\lambda _m=4\,\ell _{\mathrm{p}}/3\) (dashed line) according to standard quantum mechanics (dotted line) compared to its causal evolution (3.3) (solid line) for \(\delta t=\ell _{\mathrm{p}}\)

Full size image

3.2 Long time evolution

In order to study the time evolution for longer times, we discretise the whole interval of time by writing \(t=n\,\delta t\), where \(1\le n<N\) is a positive integer, and we recall the time step \(\delta t\) must satisfy the bound (3.6) for all relevant energies \(E\) in the spectral decomposition (3.4) and at all steps \(n\) (this will be kept under control numerically). We can then iteratively compute \(P_{\mathrm{BH}}(n\,\delta t)\) in order to determine \({\psi }_{\mathrm{S}}(r,(n+1)\,\delta t)\) by solving Eq. (3.3), or equivalently Eq. (3.5), and from that compute \(P_{\mathrm{BH}}((n+1)\,\delta t)\). This procedure can be implemented numerically in order to compute the final state \({\psi }_{\mathrm{S}}^\mathrm{fin}={\psi }_{\mathrm{S}}(r,N\,\delta t)\) starting from any given initial state \({\psi }_{\mathrm{S}}^\mathrm{in}={\psi }_{\mathrm{S}}(r,0)\).

The time evolution of the probability density \({\mathcal P}_{\mathrm{S}}\) for the same wave-packet \({\psi }_{\mathrm{S}}\) with \(m=3\,m_{\mathrm{p}}/4\) and \(\ell =\lambda _m=4\,\ell _{\mathrm{p}}/3\) shown in Fig. 2 is displayed in the left panel of Fig. 3, now at the final time \(t=10\,\ell _{\mathrm{p}}\). From this plot one can see that the packet indeed spreads more slowly than predicted by the standard free evolution, but it still gets wider and wider, so that one expects the probability for the system to be a black hole will decrease. The right panel of Fig. 3 also shows that the corresponding initial and final horizon probability densities \({\mathcal P}_{\mathrm{H}}=4\,\pi \,{r_{\mathrm{H}}}^2\,{\psi }_{\mathrm{H}}^2\) do not differ very significantly, with the peaks located roughly around the same value of \(r_{\mathrm{H}}\), in agreement with energy conservation. It is in fact more interesting to display directly the time evolution of the probability \(P_{\mathrm{BH}}=P_{\mathrm{BH}}(t)\). The latter can be seen in Fig. 4, for \(\ell =\lambda _m\), and with the same values of \(m=m_{\mathrm{p}}\), \(m=3\,m_{\mathrm{p}}/4\) and \(m=m_{\mathrm{p}}/2\) used to produce Fig. 1. It is clear that for masses \(m<m_{\mathrm{p}}\), the probability that the system remains a black hole drops very quickly in time. This could be interpreted as a decay of the initial (“fuzzy”) black hole, “without” the well-known Hawking radiation at work (or, alternatively, with the Hawking radiation mimicked by the spreading of the packet). Let us, however, notice that, even putting all of our strong simplifications aside, the results presented here would only apply to particle-like toy objects of extremely large masses \(m\sim m_{\mathrm{p}}\) and with a minimum energy \(E\simeq m\sim m_{\mathrm{p}}\), whose existence is not known in nature. Composite objects, like the more realistic BEC models of black holes of Refs. [10–17], will have to be analysed separately, and the Hawking radiation they naturally describe will then have to be explicitly accommodated for in the dynamical picture.

Fig. 3
figure 3

Left panel probability density from the final wave-packet \({\psi }_{\mathrm{S}}^\mathrm{fin}={\psi }_{\mathrm{S}}(r,10\,\ell _{\mathrm{p}})\) with \(\ell =\lambda _m\) and \(m=3\,m_{\mathrm{p}}/4\) obtained from the modified evolution (3.3) (solid line) compared to the freely evolved packet (dotted line) and initial packet \({\psi }_{\mathrm{S}}^\mathrm{in}={\psi }_{\mathrm{S}}(r,0)\) (dashed line). Right panel horizon probability density for the Gaussian particle in the left panel at \(t=0\) (dotted line) and \(t=10\,\ell _{\mathrm{p}}\) (solid line). Note that \({\psi }_{\mathrm{H}}(r_{\mathrm{H}}<r_m,t)=0\), for \(r_m=1.5\,m_{\mathrm{p}}\)

Full size image
Fig. 4
figure 4

Time evolution of the probability \(P_{\mathrm{BH}}\) for the Gaussian wave-function (2.10) with \(\ell =\lambda _m\) for \(m=m_{\mathrm{p}}\) (solid line) \(m=3\,m_{\mathrm{p}}/4\) (dashed line) and \(m=m_{\mathrm{p}}/2\) (dotted line)

Full size image

4 Conclusions

In this work, we have extended the proposal of a “horizon wave-function” \({\psi }_{\mathrm{H}}\) from Refs. [6, 7] by showing how it can also be used to describe the time evolution of a quantum system with a non-negligible probability to contain a “fuzzy” trapping surface. We have done so by assuming the evolution operator for a black hole is exactly the identity, which means no evolution would occur for an ideal state with probability \(P_{\mathrm{BH}}=1\) (the “frozen star” picture raised to the quantum level). For a general state, the time evolution is instead obtained by replacing \(\hat{H}\rightarrow (1-P_{\mathrm{BH}})\,\hat{H}\) in the Schrödinger equation. This replacement clearly preserves unitarity and also energy conservation (for isolated systems), although the coefficient \(P_{\mathrm{BH}}=P_{\mathrm{BH}}(t)\) depends on the whole wave-function \({\psi }_{\mathrm{S}}={\psi }_{\mathrm{S}}(r,t)\) [and the corresponding \({\psi }_{\mathrm{H}}={\psi }_{\mathrm{H}}(r,t)\)] and cannot therefore be simply derived from a local interaction term. One could further speculate that the proper quantum evolution operator for a black hole should describe the Hawking evaporation, thus differing from the simple identity we assumed here. As we mentioned at the end of the previous section, this aspect can likely be better addressed when considering more realistic models of black holes than the toy Gaussian particle we used here.

At the formal level, one could argue the above picture should be substantiated by providing a more detailed construction of the Hilbert spaces of the two wave-functions \({\psi }_{\mathrm{S}}\) and \({\psi }_{\mathrm{H}}\), and thoroughly analysing the properties of the operator that maps the former into the latter. This construction should indeed be possible by starting explicitly from the canonical quantisation of the relevant Einstein equation (1.3), albeit most likely in a formalism that does not make use of the Arnowitt–Deser–Misner decomposition of space-time that leads to the usual Wheeler–DeWitt equation. It might also be interesting to develop an alternative (possibly equivalent) prescription for the time evolution using a functional integral formalism, with different paths weighted by \({\psi }_{\mathrm{H}}\) or \(P_{\mathrm{BH}}\). Finally, it will certainly be important to generalise the whole approach to sources described by quantum field theory, in order to take into account known properties of standard model particles and interactions, as well as Lorentz invariance. In particular, our approach appears so far non-relativistic, in that it was always applied in the centre-of-mass reference frame in which the (forming or decaying) black hole is at rest [9], and the Planck scale is therein naturally related with the proper mass and radius of a particle [20]. These very important aspects are left for future investigations, but we would like to end by noting the key role played by localisation in this business [5]. In order to understand black hole formation and decay, it is unlikely one can neglect the spatial configuration of the physical system and just work in momentum space. This observation immediately brings to mind long-standing issues, like the very possibility of defining the position of a particle in quantum field theory [21].