New contributions to gluon poles in direct photon production

Abstract

We consider the direct photon production in a two hadron collision with one of the hadrons transversely polarized. By using the contour gauge for gluon fields, we find that there are new twist-$3$ terms present in the hadron tensor of the considered process in addition to the standard twist-$3$ terms. In this work, we demonstrate that the significance of these new terms are twofold: first, they are crucial to both the QED and the QCD gauge invariance and, second, their contributions to the hadron tensor are at least the same as those from the standard ones. We also study the resulting effects which are responsible for the universality breaking of the corresponding twist-$3$ parton distributions.

1 Introduction

The problem of the electromagnetic (QED) gauge invariance in the deeply virtual Compton scattering and similar exclusive processes has intensively been discussed during the last few years (for example, see [1–6]). This development explored the similarity with the earlier studied inclusive spin-dependent processes [7]. The gauge invariance of hard process amplitudes is ensured by twist-3 contributions and by the use of the equations of motion that provide a possibility to exclude the three-particle (quark–gluon) correlators from the amplitude. So that, after combining with the two-particle correlator contributions, one gets the gauge-invariant expressions for the physical amplitudes or, in the case of lepton–hadron processes, for the corresponding hadron tensors [7]. This scheme was originally developed in the case of the particular inclusive processes with transverse polarized hadrons, like structure function $g_2$ in DIS [7] and single spin asymmetry (SSA) [8] due to the soft quark (fermionic poles [9]). Also, the QCD gauge invariance of the so-called gluonic poles contributions [10] has been a subject of studies in [11] where the methods that are used rely on the Wilson exponentials [12–15].

We have shown in our recent work [16, 17] that, in order to ensure the QED gauge invariance of the transverse polarized Drell–Yan (DY) hadron tensor, it is mandatory to include the contribution from the extra diagram originating from the nontrivial imaginary part of the corresponding twist-$3$ function $B^V(x_1,x_2)$. Before this study [16, 17], the function $B^V(x_1,x_2)$ has been argued to be real, and the imaginary part of the amplitude was ensured by means of a specially introduced “propagator”¹ in the hard part of the hadron tensor [18]. However, we have explained in [16, 17] that the $B^V$-function does, in fact, have an imaginary part, and the existence of this imaginary part can be realized with a help of the contour gauge. Moreover, the $B^V$-function with the complex prescription induces a new contribution to the hadron tensor. As has been stressed, this extra contribution leads to the amplification of the corresponding tensor by a factor of $2$. This finding of ours has independently been confirmed in [19] by using a different approach. Besides, from the point of view of phenomenology, the corresponding SSAs in the DY process and the role of gluon pole contributions have previously been discussed in [20–35].

In the present paper, we extend our approach used in [16, 17] to the case of the direct photon production in two hadron collision where one hadron is transversely polarized. We derive the hadron tensor for this process and study the effects which lead to the soft breaking of factorization (or the universality breaking) through the QED and QCD gauge invariance. In a similar manner as in [16, 17], the special role is played by the contour gauge for gluon fields. We demonstrate that the prescriptions for the gluonic poles in the twist-$3$ correlators are dictated by the prescriptions in the corresponding hard parts. We argue that the prescriptions in the gluonic pole contributions differ from each other depending upon the initial or final state interactions (FSIs) of the diagrams under consideration. Moreover, the different prescriptions are needed to ensure the QCD gauge invariance. We treat this situation as a breaking of the universality condition resulting in factorization soft breaking. The extra diagram contributions, which naively do not have an imaginary phase, is discussed in detail.

In the paper, we also show that the new (“non-standard”) terms do contribute to the hadron tensor exactly as the “standard” terms known previously. This is exactly similar to the case of the Drell–Yan process studied in [16, 17].

2 Getting started: case of Drell–Yan process

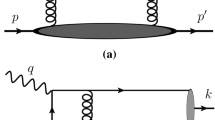
For pedagogical reasons, we recall briefly our findings for the Drell–Yan process where one of the hadrons possesses the transverse polarization; see [16, 17] for all details. As usual, the Drell–Yan process with the transversely polarized nucleon is defined as

$$\begin{aligned} N^{(\uparrow \downarrow )}(p_1) + N(p_2)\rightarrow & {} \gamma ^*(q) + X(P_X)\nonumber \\\rightarrow & {} \ell (l_1) + \bar{\ell }(l_2) + X(P_X), \end{aligned}$$

(1)

where the virtual photon producing the lepton pair ($l_1+l_2=q$) has a large mass squared ($q^2=Q^2$), while the transverse momenta are small and integrated out. The dominant light-cone directions for the DY process (Fig. 1) are defined as $p_1\approx n^*\,Q/(x_B \sqrt{2})$ and $p_2\approx n \,Q/(y_B \sqrt{2})$ with the dimensionless light-cone vectors $n^*_{\mu }=(n^{*\,+},\, 0^-,\, \mathbf{0}_\perp )$ and $n_{\mu }=(0^{+},\,n^{-} ,\, \mathbf{0}_\perp )$.

Fig. 1

The Feynman diagrams which contribute to the polarized Drell–Yan hadron tensor

Since we deal with a large $Q^2$ in the process under consideration, it is possible to apply the factorization theorem to get the corresponding hadron tensor factorized in the form of a convolution:

$$\begin{aligned}&\text {Hadron tensor} \nonumber \\&\quad = \{\text {Hard part (pQCD)}\} \{\text {Soft part (npQCD)} \}. \end{aligned}$$

(2)

Usually both the hard and the soft parts in Eq. (2) are, independent of each other, UV- and IR-renormalizable. Moreover, various parton distributions which parametrize the soft part have to manifest the universality property.

Based on the DY process, it is convenient to study the role of twist-$3$ by exploring different kinds of asymmetries, for instance, the left–right asymmetry. This left–right asymmetry means the transverse momenta of the leptons are correlated with the direction $\mathbf S \times \mathbf e _z$ where $\mathbf S _\mu$ implies the transverse polarization vector of the nucleon and $\mathbf e _z$ is a beam direction [36]. Generally speaking, any SSAs can be presented in the following symbolical form (at this moment, the exact expression for SSA is irrelevant):

$$\begin{aligned} \mathcal{A} \sim \mathrm{d}\sigma ^{(\uparrow )} - \mathrm{d}\sigma ^{(\downarrow )} \sim \mathcal{L}_{\mu \nu }\, H_{\mu \nu }, \end{aligned}$$

(3)

where $\mathcal{L}_{\mu \nu }$ is an unpolarized leptonic tensor and, consequently, has only the real part; $H_{\mu \nu }$ stands for the hadronic tensor, which is also real. Since one of the hadrons is transversely polarized, the corresponding matrix element which forms the soft part of hadron tensor reads [16, 17]

$$\begin{aligned}&\left\langle p_1, S^T | \bar{\psi }(\lambda _1 \tilde{n})\, \gamma ^+ \, g A^{\alpha }_T(\lambda _2\tilde{n}) \,\psi (0) |S^T, p_1 \right\rangle \nonumber \\&\quad = i\varepsilon ^{\alpha + S^T -} (p_1p_2) \int \mathrm{d}x_1 \mathrm{d}x_2 \, e^{i x_1\lambda _1+ i(x_2 - x_1)\lambda _2} B^V(x_1,x_2),\nonumber \\ \end{aligned}$$

(4)

where the light-cone vector $\tilde{n}$ is a dimensionful analog of the vector $n$. Therefore, in order to provide for the condition, $H_{\mu \nu }\in \mathfrak {R}\text {e}$, the complex $i$ in the r.h.s. of (4) has to be compensated for either ($a$) by the complexness of the hard part (this is the standard contribution):

$$\begin{aligned} H^{(a)}_{\mu \nu }\sim & {} i\,\mathfrak {I}\text {m}\,[ \text {Hard}] \nonumber \\&\otimes \left\{ \langle p_1,S_T|\mathcal{O}(\bar{\psi },\psi ,A) |S_T,p_1 \rangle \mathop {\sim }\limits ^{\mathcal{F}} \, i \varepsilon ^{\alpha + S_T -} B^V \right\} ,\nonumber \\ \end{aligned}$$

(5)

or ($b$) by the complexness of the soft part:

$$\begin{aligned}&H^{(b)}_{\mu \nu } \sim \text {Hard} \nonumber \\&\quad \otimes \left\{ \langle p_1,S_T|\mathcal{O}(\bar{\psi },\psi ,A) |S_T,p_1 \rangle \mathop {\sim }\limits ^{\mathcal{F}} \, i \varepsilon ^{\alpha + S_T -} \,i\,\mathfrak {I}\text {m}\,[ B^V ] \right\} .\nonumber \\ \end{aligned}$$

(6)

In Eqs. (5) and (6), $\mathop {\sim }\limits ^{\mathcal{F}}$ and $\mathcal{O}(\bar{\psi },\psi ,A)$ are the shorthands for the Fourier transformation and the corresponding quark–gluon operator, respectively [Eq. (4)]. In general, the hard parts in Eqs. (5) and (6) differ from each other. For instance, the hard part of the diagram presented in Fig. 1a contains the quark propagator in contrast to the hard part of the diagram in Fig. 1b.²

However, in the previous studies (for example [11, 18, 28–30]), $B^V(x_1,x_2)$-function has been assumed to be a purely real function:

$$\begin{aligned} B^V(x_1,x_2)= \frac{\mathcal{P}}{x_1-x_2} T(x_1,x_2)\, \end{aligned}$$

(7)

with the function $T(x_1,x_2)\in \mathfrak {R}\text {e}$ which parametrizes the corresponding projection of $\langle \bar{\psi }\, G_{\alpha \beta }\,\psi \rangle$. Therefore, the scenario (b) [Eq. (6)] will never be realized if the $B^V(x_1,x_2)$-function has the form as in Eq. (7). As a result, the QED gauge invariance of the DY hadron tensor is in question. Indeed, having analyzed the hard subprocess in the context of the QED gauge invariance, we can conclude that only the sum of two diagrams in Fig. 1a, b ensures the QED gauge invariance of the hadron tensor. As shown in [16, 17], the contribution of $H^{(a)}_{\mu \nu }$ is associated with the Feynman diagram in Fig. 1a while the contribution of $H^{(b)}_{\mu \nu }$ is generated by the diagram presented in Fig. 1b.

Thus, we may infer that the real function $B^V(x_1,x_2)$ in the form as in Eq. (7) leads to the violation of the QED gauge invariance of the hadron tensor.

To solve this discrepancy, it is instructive to recall the reason which leads to the representation in Eq. (7). The conclusion that $B^V$ is a real function has come from the ambiguity in the solutions of the differential equation (provided that $A^+=0$):

$$\begin{aligned} \partial ^+\, A^\alpha _T=G^{+\,\alpha }_T. \end{aligned}$$

(8)

Indeed, the formal solutions of Eq. (8) have the following forms:

$$\begin{aligned} A^\mu (z)= & {} \int \limits _{-\infty }^{\infty } \mathrm{d}\omega ^{-}\theta (z^{-} - \omega ^{-}) G^{+\mu } (\omega ^{-}) + A^\mu (-\infty ) \,\end{aligned}$$

(9)

$$\begin{aligned}= & {} - \int \limits _{-\infty }^{\infty } \mathrm{d}\omega ^{-} \theta (\omega ^{-} - z^{-} ) G^{+\mu } (\omega ^{-}) + A^\mu (\infty ) . \end{aligned}$$

(10)

From the first glance, Eqs. (9) and (10) seem to be equivalent each other. However, as we will see below, this is not true.

Now, if we insert Eqs. (9) and (10) into Eq. (4) and use the following parametrization:

$$\begin{aligned}&\left\langle p_1, S^T | \bar{\psi }(\lambda _1 \tilde{n})\, \gamma ^{+} \,\tilde{n}_\nu G^{\nu \alpha }_T(\lambda _2\tilde{n}) \,\psi (0) |S^T, p_1 \right\rangle \nonumber \\&\quad = \varepsilon ^{\alpha + S^T -}\,(p_1p_2) \int \mathrm{d}x_1 \mathrm{d}x_2 \, e^{i x_1\lambda _1+ i(x_2 - x_1)\lambda _2} \, T(x_1,x_2),\nonumber \\ \end{aligned}$$

(11)

we get the following representations:

$$\begin{aligned} B^V(x_1,x_2)= & {} \delta (x_1-x_2)B^V_{A(-\infty )}(x_1)+ \frac{T(x_1,x_2)}{x_1-x_2 + i\epsilon },\end{aligned}$$

(12)

$$\begin{aligned}= & {} \delta (x_1-x_2)B^V_{A(+\infty )}(x_1)+ \frac{T(x_1,x_2)}{x_1-x_2 - i\epsilon },\nonumber \\ \end{aligned}$$

(13)

respectively. In Eqs. (12) and (13), the corresponding $\pm i\epsilon$ prescriptions arise from the integral representation for the $\theta$-function:

$$\begin{aligned} \theta (\pm x) =\frac{\pm i}{2\pi } \int \limits _{-\infty }^{+\infty } \mathrm{d}k\, \frac{e^{-ikx}}{k\pm i\epsilon }. \end{aligned}$$

(14)

Further, if we suppose that the representations (12) and (13) are equivalent to each other, we can calculate the plus and minus combinations of (12) and (13) resulting in

$$\begin{aligned} B^V(x_1,x_2)= & {} \frac{1}{2}B^V(x_1,x_2) + \frac{1}{2}B^V(x_1,x_2)\nonumber \\= & {} \frac{1}{2}\delta (x_1-x_2) \Big \{B^V_{A(-\infty )}(x_1)+B^V_{A(+\infty )}(x_1)\Big \} \nonumber \\&+\frac{\mathcal{P}}{x_1-x_2}T(x_1,x_2)\, \end{aligned}$$

(15)

and

$$\begin{aligned} 0= & {} B^V(x_1,x_2)-B^V(x_1,x_2)\nonumber \\= & {} \delta (x_1-x_2) \Big \{B^V_{A(+\infty )}(x_1)-B^V_{A(-\infty )}(x_1)\Big \} \nonumber \\&-2i\,\pi \, \delta (x_1-x_2)T(x_1,x_2). \end{aligned}$$

(16)

The ambiguity in the solutions of (8) [(12) and (13)] ultimately gives us the standard representation (7) with the real function $B^V$ provided the asymmetric boundary condition for gluons is given by $B^V_{A(\infty )}(x) = - B^V_{A(-\infty )}(x)$.

In fact, the representations (12) and (13) are not equivalent ones [16, 17]. To see that, it is necessary to remember that all axial-type gauges are the particular cases of the most general contour gauge (see Appendix A and the text below for details). Using the contour gauge conception, one can easily check that the representation (12) belongs to the gauge $[x,\,-\infty ]=1$, while the representation (13) belongs to the gauge $[+\infty ,\, x]=1$. Therefore, one has no reason whatsoever to believe that (12) and (13) are equivalent [for details, see (A.12), (A.13)], i.e.

$$\begin{aligned} \{ \text {Eq. (12)}\Longrightarrow B^V_{+}(x_1,x_2)\} \not = \{ B^V_{-}(x_1,x_2) \Longleftarrow \text {Eq. (13)}\}.\nonumber \\ \end{aligned}$$

(17)

Roughly speaking, it resembles the trivial situation where two different vectors have the same projection on the certain direction. In this context, the well-known axial gauge $A^+=0$ can be treated as some type of “projection” which corresponds to two different “vectors” represented by two different contour gauges (see Appendix A).

We now consider the QED gauge-invariant hadron tensor for the DY process with the transverse polarization. In order to understand which contour gauge we need to deal with, before imposing the condition $A^+=0$, it is necessary to take into account the contributions of $\langle p_1,S^T| \bar{\psi }\, \gamma ^+\, A^+\,\psi |S^T,p_1\rangle$ in the standard hadron tensor (see Fig. 1a). Based on the analysis of the $\gamma$-structure of this diagram as shown in [16, 17], the Feynman causal prescription in the quark propagator (see Eqs. (2), (6), and (8) of [16, 17]) uniquely leads to the Wilson line in the quark–gluon correlator:

$$\begin{aligned}{}[-\infty ^-,\, 0^-] = \mathrm{Pexp}\left\{ - i g \int \limits _{-\infty }^{0} \mathrm{d}z^- \, A^+(0,z^-,\vec {\mathbf{0}}_T) \right\} . \end{aligned}$$

(18)

Equation (18) suggests that we have to use the contour gauge $[-\infty ^-,\, 0^-]=1$. Therefore, the contour gauge defined by $[-\infty ^-,\, 0^-]=1$ destroys the ambiguity, and the function $B^V(x_1,x_2)$ has to be described by the following representation (see (A.12) and [16, 17] for details):

$$\begin{aligned} B^V_{+}(x_1,x_2)= \frac{T(x_1,x_2)}{x_1-x_2 + i\epsilon }. \end{aligned}$$

(19)

As a result, the diagram represented in Fig. 1b [or the hadron tensor (6)] does contribute to the hadron tensor, and this together with the first diagram represented in Fig. 1a forms the gauge-invariant hadron tensor (see Eq. (34) of [16, 17]):

$$\begin{aligned} \overline{\mathcal{W}}_{\text {GI}}^{\mu \nu }= & {} \overline{\mathcal{W}}_{(1)}^{\mu \nu } + \overline{\mathcal{W}}_{(2)}^{\mu \nu } \nonumber \\= & {} - \frac{2}{q^2}\,\varepsilon ^{\nu S^T p_1 p_2} \, \big (x_B \, p_{1}^{\mu }- y_B\, p_{2}^{\mu }\big ) \, \bar{q}(y_B)\, T(x_B,x_B).\nonumber \\ \end{aligned}$$

(20)

From Fig. 1, we can also realize that the representation of $B^V(x_1,x_2)$ with the complex prescription $+i\,\epsilon$ in the gluonic pole, see (A.12), corresponds to the initial state interaction (ISI) with respect to the hard subprocess. We want to stress that in the case of DY process we deal with the ISI only as opposed to the case of the direct photon production which is studied below.

For the DY process, the ISI generates $-2\ell ^+ k_2^- + i\epsilon$ (see the diagram in Fig. 1a) in the quark propagator which, in turn, leads to (1) the contour gauge $[-\infty ^-,\, 0^-]=1$ and, then, to (2) the function $B^V_+$ with the certain complex prescription (A.12). The latter ensures the QED gauge invariance for the hadron tensor. Schematically, the mentioned logical chain can be presented as

$$\begin{aligned} {\text {ISI}}\Rightarrow & {} \frac{1}{-\ell ^+ + i\epsilon } \Rightarrow \text {gauge}\,\,\,[z^-,\, -\infty ^-]=1\nonumber \\\Rightarrow & {} \frac{T(x_1,x_2)}{x_1-x_2 +i\epsilon } \Rightarrow {\text {GI}}. \end{aligned}$$

(21)

We can see that the prescription in the quark propagator of the hard part gives information on the contour gauge for gluons from the soft part. In other words the hard and soft parts are not fully independent of each other. In spite of this, the DY hadron tensor has formally been factorized with the mathematical convolution, and the parton distributions, such as the twist-3 function $B^V(x_1,x_2)$, still satisfy the universality condition. In contrast to the DY process, as we will see in the next section, the direct photon production tensor is built with the functions $B^V(x_1,x_2)$, which will not manifest the universality.

We will refer to a soft breaking of the factorization when the factorization procedure results in the mathematical convolution between the finite hard and soft parts, but there is no universality for the soft functions or the hard and soft parts are not totally independent.

To conclude this section, let us note that the situation with the gauge invariance for the DY process (21) is very similar to what has been discussed for the vector meson electroproduction in [38] where the FSI also predetermined the correct prescription for the spurious gluon pole for the validity of QCD factorization.

3 Hadron tensor of the direct photon production I: kinematics and gauge invariance

3.1 Kinematics

In this section, we study the two hadron collisions, where one of the hadrons possesses the transverse polarization, which produces the direct photon in the final state in

$$\begin{aligned} N^{(\uparrow \downarrow )}(p_1) + N(p_2) \rightarrow \gamma (q) + q(k) + X(P_X). \end{aligned}$$

(22)

The gluonic poles are manifest in this process in a similar way to the Drell–Yan process [28]. We perform our calculations within a collinear factorization, and it is convenient (see, e.g., [37]) to fix the dominant light-cone directions as

$$\begin{aligned}&p_1 = \sqrt{\frac{S}{2}}\, n^*,\quad p_2 = \sqrt{\frac{S}{2}}\, n,\quad \text {with}\nonumber \\&n^*_{\mu }=(1/\sqrt{2},\,\mathbf{0}_T,\,1/\sqrt{2}), \quad n_{\mu }=(1/\sqrt{2},\,\mathbf{0}_T,\,-1/\sqrt{2}).\nonumber \\ \end{aligned}$$

(23)

The hadron momenta $p_1$ and $p_2$ have the plus and minus dominant light-cone components, respectively. Accordingly, the quark and gluon momenta $k_1$ and $\ell$ lie along the plus dominant direction, while the gluon momentum $k_2$ is along the minus direction. The final on-shell photon and quark (anti-quark) momenta can be presented as

$$\begin{aligned} \begin{aligned}&q = y_B\, \sqrt{\frac{S}{2}}\, n - \frac{q_\perp ^2}{y_B \sqrt{2 S}}\, n^* + q_\perp , \\&k = x_B\, \sqrt{\frac{S}{2}}\, n^* - \frac{k_\perp ^2}{x_B \sqrt{2 S}}\, n + k_\perp . \end{aligned} \end{aligned}$$

(24)

The Mandelstam variables for the process and subprocess are defined as

$$\begin{aligned} S= & {} (p_1+p_2)^2, \quad T=(p_1-q)^2,\quad U=(q-p_2)^2, \nonumber \\ \hat{s}= & {} (x_1p_1 + yp_2)^2 = x_1 y S, \quad \hat{t}=(x_1p_1 -q)^2=x_1 T, \nonumber \\ \hat{u}= & {} (q-yp_2)^2 = yU. \end{aligned}$$

(25)

Fig. 2

The Feynman diagram describing the hadron tensor of the direct photon production

The amplitude of process (22) involves the contributions from

• the leading (LO) diagrams: two diagrams with a radiation of the photon before ($\mathcal{A}^{\text {LO}}_1$) and after ($\mathcal{A}^{\text {LO}}_2$) the quark–gluon vertex with the gluon going to the lower blob; see the right side of Fig. 2;

• the next-to-leading order (NLO) diagrams: eight diagrams constructed from the LO diagrams by insertion of all possible radiations of the additional gluon, which together with the quark goes to the upper blob, see the left side of Fig. 2.

We denote the sum of the diagrams as

$$\begin{aligned} \mathcal{A}^{\text {LO}}_1 + \mathcal{A}^{\text {LO}}_2 + \sum \limits _{i=1}^{8}\mathcal{B}^{\text {NLO}}_i, \end{aligned}$$

(26)

which generates the hadron tensor related to the corresponding asymmetry:

$$\begin{aligned} \mathrm{d}\sigma ^\uparrow - \mathrm{d}\sigma ^\downarrow \sim \mathcal{W}= \sum \limits _{i=1}^{2}\sum \limits _{j=1}^{8} \mathcal{A}^{\text {LO}}_i \times \mathcal{B}^{\text {NLO}}_j. \end{aligned}$$

(27)

In this work, we mainly dwell on the discussion of the hadron tensor rather than the asymmetry itself. Diagrammatically (Fig. 2) the hadron tensor can be presented in the form of interference between the LO and NLO diagrams: $\mathcal{A}^{\text {LO}}_i \times \mathcal{B}^{\text {NLO}}_j$. In Fig. 2, the upper blob determines the matrix element of the twist-3 quark–gluon operator while the lower blob determines the matrix element of the twist-2 gluon operator related to the unpolarized gluon distribution.

3.2 Factorization procedure

Since the collinear factorization is our main tool, let us outline the main stages of factorization. The factorization procedure contains the following steps:

• the decomposition of loop integration momenta around the corresponding dominant direction: $k_i = x_i p + (k_i\cdot p)n + k_T$ within the certain light cone basis formed by the vectors $p$ and $n$ (in our case, $n^*$ and $n$);

• the replacement $\mathrm{d}^4 k_i \Longrightarrow \mathrm{d}^4 k_i \,\mathrm{d}x_i \delta (x_i-k_i\cdot n)$, which introduces the fractions with the appropriate spectral properties;

• the decomposition of the corresponding propagator products around the dominant direction:

  $$\begin{aligned} H(k) = H(xp) + \frac{\partial H(k)}{\partial k_\rho } \biggl |_{k=xp}\biggr . \, k^T_\rho + \cdots ; \end{aligned}$$

• the use of the collinear Ward identity, if requested by the approximation needed:

  $$\begin{aligned} \frac{\partial H(k)}{\partial k_\rho } = H_{\rho }(k,\,k) ; \end{aligned}$$

• performing of the Fierz decomposition for $\psi _\alpha (z) \, \bar{\psi }_\beta (0)$ in the corresponding space up to the needed projections.

Notice that, for our purposes, it is enough to limit ourselves by the first order of the decomposition in the third item. As a result of this procedure, we should reach the factorized form for the considered subject; see (2).

Fig. 3

The typical Feynman diagrams, contributing to the hadron tensor

3.3 Hadron tensor: QED gauge invariance

At the first item, we want to discuss the QED gauge invariance of the hadron tensor. To check the QED gauge invariance, it is sufficient to consider the typical Feynman diagrams H1, H3, and H5 represented in Fig. 3. For definiteness, we pay attention to the anti-quark contribution. All our results can trivially be extended to the quark contribution as well.

Before factorization, the H1 diagram in Fig. 3 leads to the following expression:

$$\begin{aligned}&\overline{\mathcal{W}}(\text {diag.H1})=\int (\mathrm{d}^4k_1)\,(\mathrm{d}^4k_2) \, \delta ^{(4)}(k_1+k_2-k-q) \, \Phi _g^{\alpha \beta }(k_2)\, \text {C}_2 \nonumber \\&\quad \times \,\bar{v}(k)\hat{\varepsilon }S(k+q)\gamma ^\alpha _\perp \gamma ^- \gamma ^\beta _\perp \int (\mathrm{d}^4\ell )\, S(\ell +k+q)\nonumber \\&\quad \times \,\gamma ^\rho _\perp S(k+q) \hat{q} v(k)\,\bar{\Phi }_\perp ^{[\gamma ^+],\rho }(k_1,\ell ), \end{aligned}$$

(28)

where $\text {C}_2$ implies the corresponding color factor. Here and in what follows the coupling constants are not shown explicitly. In Eq. (28) the gluon (unpolarized) twist-2 parameterizing function is defined as

$$\begin{aligned} \Phi _g^{\alpha \beta }(k_2)= & {} \int \!\!\!\!\!\!\!\sum \limits _X\,\int (\mathrm{d}^4\eta _2)\, e^{-ik_2\eta _2}\, \langle p_2| A^\alpha (0)|P_X\rangle \,\nonumber \\&\times \langle P_X | A^\beta (\eta _2) | p_2\rangle = g^{\alpha \beta }_\perp \, \mathcal{F}^g(k_2), \end{aligned}$$

(29)

while the quark–gluon twist-3 parameterizing function is given by

$$\begin{aligned}&\bar{\Phi }_\perp ^{[\gamma ^+],\rho }(k_1,\ell )= \int \!\!\!\!\!\!\!\sum \limits _X\,\int (\mathrm{d}^4\eta _1)\,(\mathrm{d}^4z)\, e^{-ik_1\eta _1-i\ell z}\,\mathrm {tr}_{D}\,\nonumber \\&\quad \times \,\langle p_1, S^T| \psi (\eta _1) |P_X\rangle \, \langle P_X | \bar{\psi }(0)\gamma ^+ A^\rho _\perp (z) | S^T, p_1\rangle .\nonumber \\ \end{aligned}$$

(30)

We now carry out the standard factorization procedure and, after some algebra, obtain the following expression:

$$\begin{aligned} \overline{\mathcal{W}}(\text {diag.H1})= & {} -2 \,\int \mathrm{d}x_1\, dy \, \delta ^{(4)}(x_1 p_1+y p_2-k-q) \, \mathcal{F}^g(y)\, \text {C}_2 \nonumber \\&\times \bar{v}(k)\hat{\varepsilon }\, \frac{\gamma ^+}{2x_1 p_1 + i\epsilon } \gamma ^- \, \int \mathrm{d}x_2\, \frac{\gamma ^+}{2x_2 p_1 + i\epsilon } \, \gamma ^\rho _\perp \nonumber \\&\times \frac{\gamma ^-}{2y p_2 + i\epsilon } \hat{q} v(k)\bar{\Phi }_\perp ^{[\gamma ^+],\rho }(x_1,x_2), \end{aligned}$$

(31)

where

$$\begin{aligned} \bar{\Phi }_\perp ^{[\gamma ^+],\rho }(x_1,x_2)= & {} \int \!\!\!\!\!\!\!\sum \limits _X\, \int (\mathrm{d}\lambda _1)\,(\mathrm{d}\lambda _2)\, e^{-ix_1\lambda _1-i(x_2-x_1)\lambda _2}\, \nonumber \\&\times \mathrm {tr}_{D}\,\langle p_1, S^T| \psi (\lambda _1 n) |P_X\rangle \, \nonumber \\&\times \langle P_X | \bar{\psi }(0)\gamma ^+ A^\rho _\perp (\lambda _2 n) | S^T, p_1\rangle \, \nonumber \\= & {} \varepsilon ^{\rho + S^T -} (p_1p_2) \, B^V(x_1,x_2). \end{aligned}$$

(32)

In the diagrams H1, H3, and H5, we deal with the FSI with respect to the hard part. Therefore, the $B^V$-function has the representation as in (A.13) (cf. [16, 17]), i.e.

$$\begin{aligned} B^V_{-}(x_1,x_2)\equiv B^V_{\text {FSI}}(x_1,x_2)=\frac{T(x_1,x_2)}{x_1 - x_2 - i\epsilon }. \end{aligned}$$

(33)

In a similar way to the preceding section, we have to restore the path in the Wilson line with $A^+$-fields in the quark–gluon correlators which appear in the diagrams H1, H3, and H5 in Fig. 3. After straightforward calculations, we derive the Wilson line in the form $[+\infty ^-,\, z^-]$, which suggests us to use the representation (A.13) for our $B^V$-function.

The contribution of H5 diagram in Fig. 3 is equal to zero due to the fact that the photon momentum has the dominant minus light-cone component and, therefore, the $\gamma$-structure gives $(\gamma ^-)^2=0$.

We now calculate the hadron tensor term associated with the H3 diagram in Fig. 3; it reads

$$\begin{aligned}&\overline{\mathcal{W}}(\text {diag.H3})= -2 \,\int \mathrm{d}x_1\, \mathrm{d}y \, \delta ^{(4)}(x_1 p_1+y p_2-k-q) \, \mathcal{F}^g(y)\, \text {C}_2 \nonumber \\&\quad \times \,\bar{v}(k)\hat{\varepsilon }\, \frac{\gamma ^+}{2x_1 p_1 + i\epsilon } \gamma ^- \hat{q} \, \int \mathrm{d}x_2\, \frac{\gamma ^-}{- 2y p_2 + i\epsilon } \nonumber \\&\quad \times \,\frac{\gamma ^+}{2x_2 p_1 + i\epsilon } \gamma ^\rho _\perp v(k)\, \bar{\Phi }_\perp ^{[\gamma ^+],\rho }(x_1,x_2), \end{aligned}$$

(34)

where the $B^V$-function is also given by the representation (33) or (A.13).

After some $\gamma$-algebra, we can check that the contribution of (34) is equal to the contribution of (31) but with an opposite sign. Therefore, the sum of all contributions gives us zero (we recall that the second diagram contribution is equal to zero itself) i.e.

$$\begin{aligned} \overline{\mathcal{W}}(\text {diag.H1})+\overline{\mathcal{W}}(\text {diag.H3})+\overline{\mathcal{W}}(\text {diag.H5})=0. \end{aligned}$$

(35)

In fact, the identity (35) reflects the QED gauge invariance for the hadron tensor. We emphasize that the QED gauge invariance occurs owing to the same complex prescriptions in the definitions of $B^V$-function (Eq. 33). In turn, the same complex prescriptions emanate from the FSI presented in H1, H3, and H5 of Fig. 3. Finally, using a similar logical chain to the DY process, we can write

$$\begin{aligned} {\text {FSI}}\Rightarrow & {} \frac{1}{\ell ^+ + i\epsilon } \Rightarrow \text {gauge}\,\,\,[+\infty ^-,\, z^- ]=1\nonumber \\\Rightarrow & {} \frac{T(x_1,x_2)}{x_1-x_2 - i\epsilon } \Rightarrow {\text {QED GI}}. \end{aligned}$$

(36)

We would like to emphasize that the concrete sign of the gluonic pole prescription is not so crucial for the QED gauge invariance because here we deal with only one type of interaction which is the FSI (this distinguishes the case of QCD gauge invariance which is considered below). It is more important to have the same prescriptions in all gluonic poles. In other words, from the point of view of contour gauge, we may use the same wrong $+i\epsilon$ prescription in the representation of $B^V$-function for diagrams H1, H3, and H5 depicted in Fig. 3. But this wrong prescription still leads to QED gauge invariance. However, after calculation of the imaginary parts for the corresponding asymmetry, the wrong prescription definitely plays a negative role.

3.4 Hadron tensor: QCD gauge invariance

We are now in a position to dwell on the QCD gauge invariance of the hadron tensor for the direct photon production. To check this invariance, we have to consider four typical diagrams H1, H5, D1, and H9, depicted in Fig. 3, which come from the corresponding $\xi$-process (see [39]). Notice that the gluon enters in the quark–gluon correlator as an internal field. For the QCD gauge invariance, we have to assume that all charged particles are on-shell, i.e. we deal with the physical gluons only. The substantial differences between this case and a pure perturbative Compton scattering case are discussed in Appendix B.

To write down the Ward identity, we need to replace the gluon transverse polarization $\epsilon ^T_\alpha$ by the gluon longitudinal momentum $\ell ^L_\alpha$ in the quark–gluon correlator:

$$\begin{aligned}&\bar{\Phi }_\perp ^{[\gamma ^+],\rho }(k_1,\ell )=- \int (\mathrm{d}^4\eta _1)\, e^{-ik_1\eta _1}\, \epsilon _T^\rho \,\nonumber \\&\quad \times \,\langle p_1, S^T| \bar{\psi }(0)\gamma ^+ \psi (\eta _1)\, a^+(\ell )| S^T, p_1\rangle \nonumber \\&\quad {\mathop {\Longrightarrow }\limits ^{\epsilon ^T\rightarrow \ell ^L}}- \int (\mathrm{d}^4\eta _1)\, e^{-ik_1\eta _1}\, \ell _L^\rho \,\langle p_1, S^T| \bar{\psi }(0)\gamma ^+ \psi (\eta _1)\, a^+(\ell )| S^T, p_1\rangle ,\nonumber \\ \end{aligned}$$

(37)

where $a^+(\ell )$ stands for the gluon creation operator. The summation over the intermediate states is not shown explicitly. Notice that the parametrization of this correlator through the $B^V$-function stays unchanged.

Consider now the contribution of the H1 diagram in Fig. 3 to the hadron tensor. Before going further, it is instructive to begin with the gluon loop integration corresponding to the mentioned diagram. We have

$$\begin{aligned} \int (\mathrm{d}^4\ell ) S(\ell +k+q) \hat{\ell }_L \langle \ldots a^+(\ell ) \ldots \rangle , \end{aligned}$$

(38)

where we do not explicitly write the operators which are irrelevant at the moment [cf. (37)]. After factorization, we obtain

$$\begin{aligned}&\int \mathrm{d}x_2 \int (\mathrm{d}^4\ell ) \delta (x_2-x_1-\ell n) S(\ell +k+q) \hat{\ell }_L \langle \ldots a^+(\ell ) \ldots \rangle \nonumber \\&\quad =\int \mathrm{d}x_2 S(x_2 p_1+yp_2) \, (x_2-x_1)\hat{p}_1 \, \int (\mathrm{d}^4\ell ) \delta (x_2-x_1-\ell n) \nonumber \\&\quad \quad \times \langle \ldots a^+(\ell ) \ldots \rangle , \end{aligned}$$

(39)

where we decompose the hard part around the dominant direction and put $\ell _L=(x_2-x_1)p_1$, which is actually dictated by the $\gamma$-structure and the momentum conservation. Using all these, we get the following expression:

$$\begin{aligned}&\overline{\mathcal{W}}(\text {diag.H1})\nonumber \\&\quad =-2 \,\int \mathrm{d}x_1\, \mathrm{d}y \, \delta ^{(4)}(x_1 p_1+y p_2-k-q) \,\mathcal{F}^g(y)\, \text {C}_2 \nonumber \\&\quad \quad \times \bar{v}(k)\hat{\varepsilon }\, \frac{\gamma ^+}{2x_1 p_1 + i\epsilon } \gamma ^- \,\int \mathrm{d}x_2\, \frac{(x_2-x_1) \gamma ^+\gamma ^-}{2x_2 + i\epsilon }\frac{\gamma ^+}{2x_1 p_1 + i\epsilon } \hat{\varepsilon }^* v(k)\nonumber \\&\quad \quad \times \left\{ (-)\int (\mathrm{d}\lambda _1)\, e^{-ix_1\lambda _1}\,\langle p_1, S^T| \bar{\psi }(0)\gamma ^+ \psi (\lambda _1 n)\,\right. \nonumber \\&\quad \quad \times \left. \int (\mathrm{d}^4\ell ) \delta (x_2-x_1-\ell n)\, a^+(\ell )| S^T, p_1\rangle \right\} , \end{aligned}$$

(40)

where

$$\begin{aligned}&(-)\int (\mathrm{d}\lambda _1)\,e^{-ix_1\lambda _1}\,\langle p_1, S^T| \bar{\psi }(0)\gamma ^+ \psi (\lambda _1 n)\,\nonumber \\&\quad \times \int (\mathrm{d}^4\ell ) \delta (x_2-x_1-\ell n) a^+(\ell )| S^T, p_1\rangle = B^V(x_1,x_2).\nonumber \\ \end{aligned}$$

(41)

It can be seen, however, that this diagram does not contribute to the Ward identity. Indeed, after calculation of the imaginary part we get the factor $(x_2-x_1)$ in the numerator of (40) which goes to zero owing to $\delta (x_2-x_1)$ from $\mathfrak {I}\text {m}B^V(x_1,x_2)$.

Further, calculation of the H5 diagram, presented in Fig. 3, gives us

$$\begin{aligned}&\overline{\mathcal{W}}(\text {diag.H5})\nonumber \\&\quad =\int \mathrm{d}x_1\, \mathrm{d}y \, \delta ^{(4)}(x_1 p_1+y p_2-k-q) \,\mathcal{F}^g(y)\, \text {C}_2 \nonumber \\&\quad \quad \times \bar{v}(k)\hat{\varepsilon }\, \frac{\gamma ^+}{2x_1 p_1 + i\epsilon } \gamma ^- \, \hat{\varepsilon }^*\nonumber \\&\qquad \times \int \mathrm{d}x_2\, \frac{\gamma ^+\gamma ^-\gamma ^+}{2x_2p_1 + i\epsilon }\, v(k)\, B^V(x_1,x_2), \end{aligned}$$

(42)

while the contribution of the D1 diagram in Fig. 3 takes the form

$$\begin{aligned}&\overline{\mathcal{W}}(\text {diag.D1})\nonumber \\&\quad =- \int \mathrm{d}x_1\, \mathrm{d}y \, \delta ^{(4)}(x_1 p_1+y p_2-k-q) \,\mathcal{F}^g(y)\, \text {C}_1 \nonumber \\&\quad \quad \times \bar{v}(k)\hat{\varepsilon }\, \frac{\gamma ^+}{2x_1 p_1 + i\epsilon } \gamma ^- \gamma ^+ \gamma ^-\,\frac{\gamma ^+}{2x_1p_1 + i\epsilon }\, \hat{\varepsilon }^*\, v(k)\nonumber \\&\qquad \times \int \mathrm{d}x_2\, \, B^V(x_1,x_2). \end{aligned}$$

(43)

Finally, the contribution of the H9 diagram with the three-gluon vertex, see Fig. 3, reads

$$\begin{aligned}&\overline{\mathcal{W}}(\text {diag.H9})\nonumber \\&\quad =-4\,i\, \int \mathrm{d}x_1\, \mathrm{d}y \, \delta ^{(4)}(x_1 p_1+y p_2-k-q) \,\mathcal{F}^g(y)\, \text {C}_3 \nonumber \\&\quad \quad \times \bar{v}(k)\hat{\varepsilon }\, \frac{\gamma ^+}{2x_1 p_1 + i\epsilon } \gamma ^- \, \frac{\gamma ^+}{2x_1p_1 + i\epsilon }\, \hat{\varepsilon }^*\, v(k)\nonumber \\&\quad \quad \times \int \mathrm{d}x_2\, \frac{x_2-x_1}{2(x_2-x_1)+i\epsilon } \, B^V(x_1,x_2). \end{aligned}$$

(44)

We now turn to the contour gauge. First of all, based on our previous discussions we notice that even a fleeting glance is sufficient to anticipate the corresponding prescriptions for the $B^V$-functions in (42)–(44). The H5 diagram in Fig. 3 corresponds to the FSI and, therefore, the function $B^V_-$ should appear here. On the other hand, the D1 and H9 diagrams in Fig. 3 correspond to the ISI which leads to the function $B^V_+$. Performing the explicit calculations (see also [16, 17]), we can arrive at the conclusion mentioned above by restoring the Wilson lines in the quark–gluon correlators of the mentioned diagrams. The Wilson line $[+\infty ^-,\, z^-]$ enters in the hadron tensor represented by the H5 diagram in Fig. 3, while the Wilson line $[z^-,\,-\infty ^- ]$, appears in the hadron tensor represented by the D1 and H9 diagrams in Fig. 3.

We sum all contributions and get the following final expression:

$$\begin{aligned}&\sum \limits _{{N=\text {H1,H5,D1,H9}}}\overline{\mathcal{W}}(\text {diag.N})\nonumber \\&\quad =\frac{\text {C}_2}{8 x_1} \gamma ^+ \gamma ^- \gamma ^+ \gamma ^- \gamma ^+\int \mathrm{d}x_2 \frac{B^V_-(x_1,x_2)}{x_2} \nonumber \\&\qquad + \frac{\text {C}_1}{8 x_1^2} \gamma ^+ \gamma ^- \gamma ^+ \gamma ^- \gamma ^+\int \mathrm{d}x_2 B^V_+(x_1,x_2) \nonumber \\&\qquad +\frac{i\text {C}_3}{4 x_1^2} \gamma ^+ \gamma ^- \gamma ^+\int \mathrm{d}x_2 \frac{(x_2-x_1) B^V_+(x_1,x_2)}{x_2-x_1+i\epsilon } \end{aligned}$$

(45)

where the function $B^V_{-}$ is represented by (A.13) or (33), and the function $B^V_+$ is given by (A.12) or

$$\begin{aligned} B^V_{+}(x_1,x_2)\equiv B^V_{\text {ISI}}(x_1,x_2)= \frac{T(x_1,x_2)}{x_1 - x_2 + i\epsilon }. \end{aligned}$$

(46)

We now calculate the imaginary part and, ultimately, we derive the QCD Ward identity in the form

$$\begin{aligned} \text {C}_2 - \text {C}_1 - i\text {C}_3 = - [t^a, t^b]\, t^b\, t^a + i f^{abc} t^c\, t^b\, t^a \equiv 0. \end{aligned}$$

(47)

We want to stress that the identity (47) occurs provided only the presence of the different complex prescriptions in gluonic poles dictated by the final or ISIs:

$$\begin{aligned}&\left. \begin{array}{l} {\text {FSI}}\Rightarrow \frac{1}{\ell ^+ + i\epsilon } \Rightarrow \text {gauge}\,\,\,[+\infty ^-,\, z^- ]=1 \Rightarrow \frac{T(x_1,x_2)}{x_1-x_2 - i\epsilon }\,\\ {\text {ISI}}\Rightarrow \frac{1}{-\ell ^+ + i\epsilon } \Rightarrow \text {gauge}\,\,\,[z^-,\, -\infty ^-]=1 \Rightarrow \frac{T(x_1,x_2)}{x_1-x_2 +i\epsilon }\,\\ \end{array}\right\} \nonumber \\&\quad \Rightarrow {\text {QCD} \text {GI}}. \end{aligned}$$

(48)

We emphasize the principal differences (see details in Appendix B) between the considered case and the proof of the QCD gauge invariance for the perturbative Compton scattering amplitude with the physical gluons in the initial and final states. The latter does not need any external condition such as the presence of gluon poles.

Thus, the situation which we discuss is again absolutely similar to that one which has been described in [38] for the dijet production. From (48), it is seen that the different diagrams correspond to the different contour gauges and, consequently, to the different functions, $B^V_{\pm }$, which parametrize the hadronic matrix element forming the soft part. In this context, we also have a soft breaking of factorization because, first, it spoils the universality principle and, second, the gluonic pole prescriptions in the soft part are traced to the causal prescriptions in the hard part. At the same time, we can use the replacement [38]

$$\begin{aligned} \frac{T(x_1,x_2)}{x_1-x_2 - i\epsilon } = \frac{T(x_1,x_2)}{x_1-x_2 + i\epsilon } + 2\pi \, i\, \delta (x_1-x_2)T(x_1,x_2)\nonumber \\ \end{aligned}$$

(49)

and finally get the same function $B^V_+$ for all diagrams (in other words, we can use the same contour gauge for all diagrams). However, it contains the additional $\delta (x_1-x_2)$-term which may lead to the collinear factorization violation in the same manner as in [38]. The full analysis of this case will be implemented in our forthcoming work.

4 Hadron tensor of the direct photon production II: new contributions

In this section we calculate the full expression for the hadron tensor, which involves both the standard and the new contributions to the gluon pole terms. The full expression for the hadron tensor related to the case we are discussing can be split into two groups: (1) the first type of contributions corresponds to the diagrams H1–H12 depicted in Fig. 3 and, before factorization, takes the following form:

$$\begin{aligned} \mathcal{W}(\text {diag.H})= & {} \int \frac{\mathrm{d}^3 \vec {q}}{(2\pi )^3 2 E} \frac{\mathrm{d}^3 \vec {k}}{(2\pi )^3 2 \varepsilon } \, \text {C}_H\, \nonumber \\&\times \int (\mathrm{d}^4 k_1) (\mathrm{d}^4 k_2) \delta ^{(4)}(k_1+k_2-q-k)\, \Phi _g^{\alpha \beta }(k_2) \nonumber \\&\times \int (\mathrm{d}^4\ell )\, \Phi ^{[\gamma ^+],\,\rho }_\perp (k_1,\ell )\, H^{\alpha \beta , \rho }(k_1,k_2,\ell ), \end{aligned}$$

(50)

and (2) the second type of contributions, given by the diagrams D1–D4 in Fig. 3, can be presented as

$$\begin{aligned} \mathcal{W}(\text {diag.D})= & {} \int \frac{\mathrm{d}^3 \vec {q}}{(2\pi )^3 2 E} \frac{\mathrm{d}^3 \vec {k}}{(2\pi )^3 2 \varepsilon } \, \text {C}_D\, \nonumber \\&\times \int (\mathrm{d}^4 k_1) (\mathrm{d}^4 k_2) \delta ^{(4)}(k_1+k_2-q-k)\nonumber \\&\times \Phi _g^{\alpha \beta }(k_2)\, \mathrm{tr}_{ D}\big [ \Phi ^{(1)}(k_1)\, \mathrm{d}^{\alpha \beta }(k_1,k_2)\big ] . \end{aligned}$$

(51)

In Eqs. (50) and (51), the corresponding coefficient functions are denoted by $H_{\alpha \beta , \rho }(k_1,k_2,\ell )$ and $D_{\alpha \beta }(k_1,k_2)$. The unpolarized twist-$2$ gluon distribution $\Phi ^g(k_2)$ and the twist-$3$ quark distribution $\Phi _\perp ^{[\gamma ^+],\rho }(k_1,\ell )$ are defined in the standard forms; see (29) and (30). The twist-$3$ quark distribution which appears in the diagrams D1–D4 presented in Fig. 3 is given by

$$\begin{aligned} \Phi ^{(1)}(k_1)= & {} \frac{\gamma ^+ \gamma ^\rho _\perp \, \gamma ^-}{2k_1^++i\epsilon }\, \int (\mathrm{d}^4\eta _1)\, e^{ik_1\eta _1}\,\nonumber \\&\times \langle p_1, S^T| \bar{\psi }(0)\gamma ^+ A^\rho _\perp (0)\psi (\eta _1) | S^T, p_1\rangle , \end{aligned}$$

(52)

where the sum over the corresponding intermediate states is implied. We now perform the factorization procedure for Eqs. (50) and (51), and we obtain

$$\begin{aligned} \mathrm{d}{\mathcal W}(\hbox {diag.H})= & {} \frac{\mathrm{d}^3 \vec {q}}{(2\pi )^3 2 E} \int \frac{\mathrm{d}^3 \vec {k}}{(2\pi )^3 2 \varepsilon } \delta ^{(2)}(\vec {\mathbf{k}}_\perp +\vec {\mathbf{q}}_\perp ) \, \hbox {C}_H\, \nonumber \\&\times \int \mathrm{d}x_1 \mathrm{d}y \delta (x_1-x_B)\,\delta (y-y_B)\,\frac{2}{S} \mathcal{F}^g(y)\,g_\perp ^{\alpha \beta }\nonumber \\&\times \int \mathrm{d}x_2\, \Phi ^{[\gamma ^+],\,\rho }_\perp (x_1,x_2)\, H^{\alpha \beta , \rho }(x_1,x_2) \end{aligned}$$

(53)

for the first type of contributions, and

$$\begin{aligned} \mathrm{d}{\mathcal W}(\hbox {diag.D})= & {} \frac{\mathrm{d}^3 \vec {q}}{(2\pi )^3 2 E} \int \frac{\mathrm{d}^3 \vec {k}}{(2\pi )^3 2 \varepsilon } \delta ^{(2)}(\vec {\mathbf{k}}_\perp +\vec {\mathbf{q}}_\perp ) \, \hbox {C}_D \nonumber \\&\times \int \mathrm{d}x_1 \mathrm{d}y \delta (x_1-x_B)\,\delta (y-y_B)\,\nonumber \\&\times \frac{2}{S} \mathcal{F}^g(y)\,g_\perp ^{\alpha \beta }\, {\mathrm{tr}}_{ D}\big [\Phi ^{(1)}(x_1)\, \mathrm{d}^{\alpha \beta }(x_1)\big ] \end{aligned}$$

(54)

for the second type of contributions.

To simplify our calculations without losing generality, we may choose the frame where $q_\perp ^2\ll S$. The Mandelstam variable defined for the subprocess, $\hat{u}$, is a small variable and can be neglected. It means that the Bjorken fraction $y_B$ becomes independent of $x_B$, and one can write $y_B=-T/S$ (due to $\hat{s} + \hat{t} + \hat{u} =0$).

The next stage is to determine the type of the twist-$3$ function $B^V(x_1,x_2)$ which is related to certain complex prescriptions in the gluon poles according to the way described in the preceding sections. The correct definition of the $B^V(x_1,x_2)$-function should be implemented for each of diagrams. Also, it is instructive to notice that the diagrams H1–H8 would not possess the gluon poles in the case where the function $B^V$ is assumed to be a real one. However, this is not true in our case.

After computing the corresponding traces and performing some simple algebra within the frame we are choosing, it turns out that the only nonzero contributions to the hadron tensor come from the diagrams H1, H7, D4, and H10:

$$\begin{aligned} \mathrm{d}\mathcal{W}(\hbox {diag.H1})= & {} \frac{\mathrm{d}^3 \vec {q}}{(2\pi )^3 2 E} \int \frac{\mathrm{d}^3 \vec {k}}{(2\pi )^3 2 \varepsilon } \delta ^{(2)}(\vec {\mathbf{k}}_\perp +\vec {\mathbf{q}}_\perp ) \, \hbox {C}_2\, \nonumber \\&\times \int \mathrm{d}x_1 \mathrm{d}y \delta (x_1-x_B)\,\delta (y-y_B)\, \mathcal{F}^g(y)\nonumber \\&\times \int \mathrm{d}x_2\, \frac{2 S^2\, x_1 \, y^2}{[x_2 y S + i\epsilon ][x_1 y S + i\epsilon ]^2}\, \frac{\varepsilon ^{q_\perp + S_\perp -}}{p_1^+}\, \nonumber \\&\times B^{V}_-(x_1,x_2), \end{aligned}$$

(55)

$$\begin{aligned} \mathrm{d}\mathcal{W}(\hbox {diag.H7})= & {} \frac{\mathrm{d}^3 \vec {q}}{(2\pi )^3 2 E} \int \frac{\mathrm{d}^3 \vec {k}}{(2\pi )^3 2 \varepsilon } \delta ^{(2)}(\vec {\mathbf{k}}_\perp +\vec {\mathbf{q}}_\perp ) \, \hbox {C}_1\, \nonumber \\&\times \int \mathrm{d}x_1 \mathrm{d}y \delta (x_1-x_B)\,\delta (y-y_B)\, \mathcal{F}^g(y) \nonumber \\&\times \int \mathrm{d}x_2\, \frac{(-2) S\, T\, x_1\, (y-3y_B)}{[x_2 T + i\epsilon ][x_1 T + i\epsilon ]^2}\, \frac{\varepsilon ^{q_\perp + S_\perp -}}{p_1^+}\, \nonumber \\&\times B^{V}_+(x_1,x_2), \end{aligned}$$

(56)

$$\begin{aligned} \mathrm{d}\mathcal{W}(\hbox {diag.D4})= & {} \frac{\mathrm{d}^3 \vec {q}}{(2\pi )^3 2 E} \int \frac{\mathrm{d}^3 \vec {k}}{(2\pi )^3 2 \varepsilon } \delta ^{(1)}(\vec {\mathbf{k}}_\perp +\vec {\mathbf{q}}_\perp ) \, \hbox {C}_1\, \nonumber \\&\times \int \mathrm{d}x_1 \mathrm{d}y \delta (x_1-x_B)\,\delta (y-y_B)\,\frac{2}{S} \mathcal{F}^g(y) \nonumber \\&\times \frac{2 S^2 \,x_1\, (y-2y_B)}{[x_1 T + i\epsilon ]^2}\, \frac{\varepsilon ^{q_\perp + S_\perp -}}{2x_1p_1^+ + i\epsilon }\, \int \mathrm{d}x_2\,\nonumber \\&\times B^{V}_+(x_1,x_2), \end{aligned}$$

(57)

and

$$\begin{aligned} \mathrm{d}\mathcal{W}(\hbox {diag.H10})= & {} \frac{\mathrm{d}^3 \vec {q}}{(2\pi )^3 2 E} \int \frac{\mathrm{d}^3 \vec {k}}{(2\pi )^3 2 \varepsilon } \delta ^{(2)}(\vec {\mathbf{k}}_\perp +\vec {\mathbf{q}}_\perp ) \,\hbox {C}_3\, \nonumber \\&\times \int \mathrm{d}x_1 \mathrm{d}y \delta (x_1-x_B)\,\delta (y-y_B)\, \mathcal{F}^g(y) \nonumber \\&\times \int \mathrm{d}x_2\, \frac{2 T (x_1-x_2) (2 T+S y)}{[x_1 T + i\epsilon ][x_2 T + i\epsilon ][(x_1-x_2) y S + i\epsilon ]}\, \nonumber \\&\times \frac{\varepsilon ^{q_\perp + S_\perp -}}{p_1^+}\, B^{V}_+(x_1,x_2). \end{aligned}$$

(58)

Here, $\hbox {C}_1=C_F^2 N_c$, $\hbox {C}_2=-C_F/2$, $\hbox {C}_3=C_F\, N_c \,C_A/2$. The other diagram contributions disappear owing to the following reasons: (1) the $\gamma$-algebra gives $(\gamma ^-)^2=0$; (2) the common pre-factor $T+yS$ goes to zero, (3) the diagrams H2 and H5 cancel each other.

Analyzing the results for the diagrams H1, H7, D4, and H10 [see Eqs. (55)–(58)], we see that

$$\begin{aligned}&\mathrm{d}\mathcal{W}(\hbox {diag.H1}) + d\mathcal{W}(\hbox {diag.H7}) + d\mathcal{W}(\hbox {diag.D4}) \nonumber \\&\quad = d\mathcal{W}(\hbox {diag.H10}). \end{aligned}$$

(59)

In other words, similar to the Drell–Yan process, the new (“non-standard”) contributions generated by the diagrams H1, H7, and D4 result again in the factor of $2$ compared to the “standard” diagram H10 contribution to the corresponding hadron tensor. This is our principal result.

5 Conclusions

In this work, we explore both the QED and the QCD gauge invariance of the hadron tensor for the direct photon production in two hadron collision where one of the hadrons is transversely polarized. We present the important details related to the use of the contour gauge for the Drell–Yan process with essential transverse polarizations. We study the effects which lead to the soft breaking of factorization through the QED and QCD gauge invariance.

We show that the contour gauges for gluon fields play the crucial role for our study. The contour gauge belongs to the class of non-local gauges that depends on the path connecting two points in the correlators. It turns out, in the cases which we consider, the prescriptions for the gluonic poles in the twist-$3$ correlators are dictated by the prescriptions in the corresponding hard parts in a similar manner to the DY process considered in [16, 17].

For the direct photon production, we demonstrate that the prescriptions in the gluonic pole contributions differ from each other, depending upon the initial or FSIs in the related diagrams. We stress that the different prescriptions are needed to ensure the QCD gauge invariance. This situation has been treated as a soft breaking of the universality condition, resulting in factorization breaking. Besides, the presence of the complex prescriptions in the gluonic pole contributions allow the extra diagrams to contribute nontrivially to the hadron tensor.

We find that the “non-standard” new terms, which exist in the case of the complex twist-$3$ $B^V$-function with the corresponding prescriptions, do contribute to the hadron tensor exactly as the “standard” term known previously. This is another important result of our work. We also observe that this is exactly similar to the case of the Drell–Yan process studied in [16, 17].

Appendices

Appendix A: $B^V(x_1,x_2)$-function within the contour gauge

In this appendix we give some details regarding the use of the contour gauge. The solution of the QED gauge-invariance problem for the DY hadron tensor can be found by using the contour gauge conception (see, for example, [16, 17, 40–42]). Here, we would like to demonstrate that there is no an ambiguity in the integral representation of the gluon fields through the strength tensor [Eqs. (9) and (10)]. It is important to note that the axial gauge condition, $A^+=0$ (as well as the Fock–Schwinger gauges) is actually a particular case of the most general contour gauge where the Wilson line with an arbitrary path determines the gauge transformations. The contour gauge was the subject of very intense studies many years ago. The significance of the use of the contour gauge is that the quantum gauge theory becomes free from the Gribov ambiguities.

Let us briefly discuss the main items of the contour gauge conception. To describe this class of gauges, it is instructive to assume the geometrical interpretation of gluons where the gluon field is a connection of the principal fiber bundle $\mathcal{P}(\mathbb {R}^4, G, \pi )$ (here, $\mathbb {R}^4$ implies the base where the principal fiber bundle is determined, $G$ denotes the group defined on the given fiber and $\pi$ is a transformation of the base $\mathbb {R}^4$ into the fiber bundle $\mathcal{P}$). Each element $\mathbf {g}(x)$ of the fiber, with the help of the gluon field $A_\alpha$, defines the gauge-transformed field:

$$\begin{aligned} A^{\mathbf {g}}_\mu (x)=\mathbf {g}^{-1}(x)A_{\mu }(x) \mathbf {g}(x) + \frac{i}{g}\mathbf {g}^{-1}(x)\partial _{\mu }\mathbf {g}(x). \end{aligned}$$

(A.1)

The set of these fields for all $\mathbf {g}(x)$ forms the orbit of the gauge-equivalent fields. It is well known that in order to quantize the system of the gauge fields, one has to choose the only element of each orbit. In contrast to the usual way, we first fix an arbitrary point $(x_0, \mathbf {g}(x_0))$ ³ in the fiber. Then, we define two directions: one of them in the base, the other in the fiber. The direction in the base $\mathbb {R}^4$ is nothing else than the tangent vector of a curve which goes through the given point $x_0$. At the same time, the direction in the fiber can be uniquely determined as the tangent subspace which is related to the parallel transition. After following this procedure, one can uniquely define the point in the fiber bundle.

Further, solving the parallel transport equation which is defined on the fiber as

$$\begin{aligned} \frac{\mathrm{d}x_\alpha (v)}{\mathrm{d}v} \, \mathcal{D}_\alpha \mathbf {g}(x(v)) = 0, \end{aligned}$$

(A.2)

one can find the solution in terms of the Wilson line:

$$\begin{aligned} \mathbf g (x)=\mathrm{Pexp}\left\{ ig \int \limits _{\mathbb {P}(x_0,x)} \mathrm{d}\omega \cdot A(\omega )\right\} \mathbf g (x_0) , \end{aligned}$$

(A.3)

where the points $x_0$ and $x$ are connected by the path $\mathbb {P}$. The starting point $x_0$ is usually fixed, i.e. $x_0$ is independent on $x$. Here, $\mathbf g (x_0)$ is chosen to be equal to unity.⁴ Note that the fixing of $\mathbf g (x)$ ensures a unique choice of the element in the orbit. Inserting (A.3) into (A.1), one can see that the field $A^\mathbf{g }_\mu (x)$ is completely determined by the form of the path which connects the starting and final points. Moreover, using (A.1) and (A.3), one obtains the property

$$\begin{aligned}&\mathrm{Pexp}\left\{ ig \int \limits _{x_0}^{x} \mathrm{d}\omega \cdot A^\mathbf{g }(\omega )\right\} \nonumber \\&\quad = \mathbf g ^{-1}(x) \mathrm{Pexp}\left\{ ig \int \limits _{x_0}^{x} \mathrm{d}\omega \cdot A(\omega )\right\} \mathbf g (x_0) . \end{aligned}$$

(A.4)

Inserting Eq. (A.3) into Eq.(A.1) (we recall that the point $x_0$ is fixed), we arrive at

$$\begin{aligned} A^\mathbf{g }_\mu (x)= & {} \int \limits _{\mathbb {P}(x_0,x)} \mathrm{d}z_\alpha \frac{\partial z_\beta }{\partial x_\mu }\, \mathbf g ^{-1}(z) \,G_{\alpha \beta }(z| A)\, \mathbf g (z)\nonumber \\= & {} \int \limits _{\mathbb {P}(x_0,x)} \mathrm{d}z_\alpha \frac{\partial z_\beta }{\partial x_\mu }\, G_{\alpha \beta }(z| A^\mathbf{g }) , \end{aligned}$$

(A.5)

where

$$\begin{aligned} G_{\alpha \beta }(z| A^\mathbf{g })\equiv G_{\alpha \beta }^\mathbf{g }(z) =\mathbf g ^{-1}(z) \,G_{\alpha \beta }(z| A)\, \mathbf g (z). \end{aligned}$$

(A.6)

The contour gauge condition demands that $\mathbf g (x)$ is equal to unity for all $x$ belonging to the base, i.e.

$$\begin{aligned}{}[x,\,x_0]\mathop {=}\limits ^{\mathrm{def}}\mathrm{Pexp}\left\{ ig \int \limits _{x_0}^{x} \mathrm{d}\omega \cdot A(\omega )\right\} = 1 , \quad \forall x \in \mathbb {R}^4 . \end{aligned}$$

(A.7)

Therefore, within the contour gauge, the field $A^\mathbf{g }_\mu$ [see (A.5)] becomes

$$\begin{aligned} A^{c.g.}_\mu (x)= \int \limits _{\mathbb {P}(x_0,x)} \mathrm{d}z_\alpha \frac{\partial z_\beta }{\partial x_\mu }\, G_{\alpha \beta }(z| A) , \end{aligned}$$

(A.8)

i.e. the gluon field $A^\mathbf{g }_\mu$ is a linear functional of the tensor $G_{\mu \nu }$. Let us briefly comment on the choice of the boundary conditions for the gluons. As is pointed out in [40], the starting point $x_0$ of the path ${\mathbb {P}(x_0,x)}$ [see (A.8)] is not well defined by construction. In turn, this leads to the presence of the so-called residual gauge transformation. To avoid this ambiguity, it is natural to fix the uncertainty in Eq. (A.8) by $A_{\mu }(x_0)=0$. In other words, the starting point is fixed, and it is independent from the destination of the path ${\mathbb {P}(x_0,x)}$.

It is easy to see that the representations (9) and (10) (or the representations (12) and (13)) can be derived from (A.8) by fixing of the path $\mathbb {P}(x_0,x)$ as a straight line connecting the point $x$ with $\mp \,\infty$, respectively. In fact, it means that the representations (12) and (13) correspond to two different contour gauges and give us two different representations for two different functions $B^V_{-}(x_1,x_2)$ and $B^V_{+}(x_1,x_2)$. These two representations are associated with the final and ISIs [Eqs. (33) and (46)].

Moreover, in order to get a concrete representation for gluons within the axial gauge, we can explicitly parametrize the straight line between the points $x$ and $\pm \infty$ along the “minus” light-cone direction $n^-$:

$$\begin{aligned} x_\alpha (s)\Big |_{x}^{\pm \infty } = x_\alpha \pm n_\alpha \,\lim _{\epsilon \rightarrow 0} \frac{1-e^{-\epsilon s}}{\epsilon } \Big |_{0}^{+\infty }. \end{aligned}$$

(A.9)

Then, using Eq. (A.8), one gets

$$\begin{aligned} A^{ax_{\pm }}_\mu (x)=\mp \, n_\alpha \int \limits _0^\infty \mathrm{d}s \, G_{\alpha \mu }(x\pm ns)\, e^{-\epsilon s}\Big |_{\epsilon \rightarrow 0}. \end{aligned}$$

(A.10)

Based on the contour gauge, the representations (A.10) determine two different contour gauges: $A^{ax_{+}}_\mu (x)$ corresponds to the straight line between $x$ and $+\infty$, and $A^{ax_{-}}_\mu (x)$ corresponds to the line between $-\infty$ and $x$. Moreover, their projections on the light-cone vector $n^-$ are the same:

$$\begin{aligned} n\cdot A^{ax_\pm }(x)=A^+=0. \end{aligned}$$

(A.11)

Thus, we can conclude that the r.h.s. of (12) and (13) correspond to the different functions $B^V_{\pm }(x_1,x_2)$:

$$\begin{aligned} B^V_{+}(x_1,x_2)= & {} \delta (x_1-x_2)B^V_{A(-\infty )}(x_1)+ \frac{T(x_1,x_2)}{x_1-x_2 + i\epsilon }\nonumber \\&\text {for the gauge } [x,\,-\infty ]=1, \end{aligned}$$

(A.12)

$$\begin{aligned} B^V_{-}(x_1,x_2)= & {} \delta (x_1-x_2)B^V_{A(+\infty )}(x_1)+ \frac{T(x_1,x_2)}{x_1-x_2 - i\epsilon }\nonumber \\&\text {for the gauge } [+\infty ,\, x]=1. \end{aligned}$$

(A.13)

It is clear that these two representations cannot be equivalent. Also, it is reasonable to assume the zeroth boundary conditions for the gluons to be $B^V_{A(\pm \infty )}=0$, which is in agreement with Refs. [16, 17, 40–42]. Note that the functions $B^V_{\pm }$ do not possess a certain property under the time-reversal transformation. This property becomes a well-defined one only after calculation of the imaginary part for the hadron tensor.

We thus have no the ambiguity in the solutions of (8). As a result, the $B^V$-function has a nontrivial imaginary part which contributes to $H^{(b)}_{\mu \nu }$ needed for the gauge-invariant set.

Appendix B: Comparison with the perturbative Compton scattering amplitude

In this appendix, we discuss an essential difference between the QCD gauge invariance for the “perturbative” Compton amplitude, $\langle q(k)g(\ell )|\, \mathbb {S} \,| g(k_2) q(k_1)\rangle$, and the “nonperturbative” analog of Compton amplitude, $\langle X(P_X)q(k)|\, \mathbb {S} \,| g(k_2) A(P)\rangle$, where one of gluons is included in the loop integration (see Figs. 4, 5).

1.1 B.1: QCD gauge invariance of the perturbative Compton amplitude

We first consider the “perturbative” Compton amplitude represented in Fig. 4.

Fig. 4

Compton diagrams without the blob (the “perturbative” case)

To prove the QCD gauge invariance, we assume that all gluons are physical ones with the transverse polarizations. The first diagram in Fig. 4 gives us

$$\begin{aligned} \mathcal{A}_{\alpha \beta }(\text {dia.1})= & {} (-i)g\, \bar{u}(k) \gamma _\beta \,\frac{\hat{k}_1 + \hat{k}_2}{(k_1+k_2)^2+i\epsilon }\, \gamma _{\alpha } \,t^a\,t^b\, u(k_1), \quad \nonumber \\ \mathcal{A}(\text {dia.1})= & {} \mathcal{A}_{\alpha \beta }(\text {dia.1}) \epsilon ^\perp _\alpha \, \epsilon ^{*\,\perp }_\beta . \end{aligned}$$

(B.1)

To check the gauge invariance with respect to, for example, the physical gluon with momentum $\ell$, we have to replace the given polarization vector $\epsilon ^{*\,\perp }_\beta$ on the momentum $\ell _\beta$, provided $\ell \cdot \epsilon ^{*\,\perp }=0$, in the amplitude (B.1). We have

$$\begin{aligned} \mathcal{A}(\text {dia.1})=(-i)g\, \bar{u}(k) \hat{\ell }\, \frac{\hat{k}_1 + \hat{k}_2}{(k_1+k_2)^2+i\epsilon } \hat{\epsilon }^\perp \,t^a\,t^b\, u(k_1).\nonumber \\ \end{aligned}$$

(B.2)

Using the momentum conservation, $k_1+k_2=k+\ell$, and the corresponding equations of motion, Eq. (B.2) reduces to the following form:

$$\begin{aligned} \mathcal{A}(\text {dia.1})= & {} (-i)g\,\bar{u}(k)\, [\hat{k}_1 + \hat{k}_2 + \hat{k}] \nonumber \\&\times \frac{\hat{k}_1 + \hat{k}_2}{(k_1+k_2)^2+i\epsilon } \hat{\epsilon }^\perp \,t^a\,t^b\, u(k_1)\nonumber \\= & {} \bar{u}(k) \,\hat{\epsilon }^\perp \,t^a\,t^b\, u(k_1). \end{aligned}$$

(B.3)

In a similar way, we can get the contribution of the second diagram presented in Fig. 4. It reads

$$\begin{aligned} \mathcal{A}(\text {dia.2})= & {} (-i)g\,\bar{u}(k)\,\hat{\epsilon }^\perp \,\frac{ \hat{k}_1 - \hat{\ell }}{ (k_1 - \ell )^2+i\epsilon } \hat{\ell }\,t^b\,t^a\, u(k_1)\nonumber \\= & {} - \,\bar{u}(k) \,\hat{\epsilon }^\perp \,t^b\,t^a\, u(k_1). \end{aligned}$$

(B.4)

Therefore, the sum of these two diagrams gives us the color commutator:

$$\begin{aligned} \mathcal{A}(\text {dia.1}) + \mathcal{A}(\text {dia.2})=(-i)g\,\bar{u}(k) \,\hat{\epsilon }^\perp \,[t^a,\,t^b]\, u(k_1). \end{aligned}$$

(B.5)

Fig. 5

Compton diagrams with the blob (the “nonperturbative” case)

In the Feynman gauge,⁵ the third diagram in Fig. 4 contributes as (here we again replace the transverse gluon polarization on the gluon momentum: $\epsilon ^{*\,\perp }\rightarrow \ell$)

$$\begin{aligned} \mathcal{A}(\text {dia.3})= & {} ig\, \bar{u}(k) \,\gamma _\sigma \,t^c\, u(k_1) \frac{1}{(k-k_1)^2+i\epsilon }if^{acb}\nonumber \\&\times V_{\alpha \sigma \beta }(-k_2; k-k_1; \ell ) \epsilon ^\perp _\alpha \ell _\beta , \end{aligned}$$

(B.6)

where

$$\begin{aligned} V_{\alpha \sigma \beta }(-k_2; k-k_1; \ell )= & {} g_{\alpha \sigma } (k-k_1+k_2)_\beta \nonumber \\&+ g_{\sigma \beta }(\ell -k+k_1)_\alpha - g_{\alpha \beta }(k_2+\ell )_\sigma .\nonumber \\ \end{aligned}$$

(B.7)

Making use of $\epsilon ^\perp \cdot \ell =\epsilon ^{*\,\perp }\cdot \ell =0$ and

$$\begin{aligned} \frac{(k-k_1+k_2)\cdot \ell }{(k-k_1)^2}=\frac{k_2\cdot \ell }{(k_2-\ell )^2}=-1, \end{aligned}$$

(B.8)

we obtain

$$\begin{aligned} \mathcal{A}(\text {dia.3})=i^2g\, f^{abc} \bar{u}(k)\hat{\epsilon }^\perp \, t^c\, u(k_1). \end{aligned}$$

(B.9)

The sum of all three diagrams leads to

$$\begin{aligned} \mathcal{A}(\text {dia.1})+\mathcal{A}(\text {dia.2})+\mathcal{A}(\text {dia.3})=0, \end{aligned}$$

(B.10)

which ensures the QCD gauge invariance. In the case of the “perturbative” Compton amplitude with physical gluons, the momentum conservation, $\delta ^{(4)}(k_1+k_2-\ell -k)$, and the on-shellness of all external particles play important roles for checking of the gauge invariance.

1.2 B.2: QCD gauge invariance of the nonperturbative Compton scattering amplitude

In order to get the diagrams in Fig. 5, we now attach the nonperturbative blobs to the diagrams in Fig. 4.

In contrast to the “perturbative” Compton amplitude, the gluon with momentum, $\ell$, with respect to which we check the gauge invariance, is included in the loop integration. As a result, the momentum conservation for the subprocess has the form $k_1+k_2=k$.

Let us focus on two diagrams in Fig. 5 which are enough to demonstrate how the color commutator contribution can be formed. Both diagrams are given by

$$\begin{aligned}&\langle X(P_X)q(k)|\, \mathbb {S} \,| g(k_2) A(P)\rangle \nonumber \\&\quad = \bar{u}(k)\epsilon ^\perp _\alpha \int (\mathrm{d}^4\xi )(\mathrm{d}^4\eta ) e^{-ik_2\xi +ik\eta } \langle P_X | \frac{\delta ^2 \mathbb {S}}{\delta \bar{\psi }(\eta )\delta A_\alpha (\xi )}| P\rangle \Big |_{\psi =\cdots =A=0}.\nonumber \\ \end{aligned}$$

(B.11)

The first diagram in Fig. 5 contributes as

$$\begin{aligned} \mathcal{B}(\text {dia.1})= & {} \bar{u}(k) \int (\mathrm{d}^4\ell ) \gamma _\beta S(\ell +k)\hat{\epsilon }^\perp \nonumber \\&\times \int (\mathrm{d}^4\eta ) e^{-i\ell \eta } \langle P_X| A_{\beta }(\eta ) \,t^a\,t^b\, \psi (0)|P\rangle . \end{aligned}$$

(B.12)

This expression corresponds to the amplitude before factorization and, therefore, the quark with $k_1+\ell$ and gluon with $\ell$ are off-shell. Next, we apply the factorization procedure and derive the following expression for the first diagram contribution (here we use the light-cone basis presented above):

$$\begin{aligned}&\mathcal{B}(\text {dia.1}) \nonumber \\&\quad =\bar{u}(k) \int \mathrm{d}x_2 (x_{2}-x_1)\hat{n}^* S\big ((x_2-x_1)n^* + k\big )\hat{\epsilon }^\perp \, t^a\,t^b\, u(x_2n^*) \nonumber \\&\quad \quad \times \langle P_X | a^+\big ((x_2-x_1)n^*\big ) b^-(x_2n^*) |P\rangle \end{aligned}$$

(B.13)

or

$$\begin{aligned} \mathcal{B}(\text {dia.1})= & {} \bar{u}(k)\int \mathrm{d}x_2 \gamma ^-\,\gamma ^+ \hat{\epsilon }^\perp \, t^a\,t^b\, u(x_2n^*)\nonumber \\&\times \langle P_X | a^+\big ((x_2-x_1)n^*\big ) b^-(x_2n^*) |P\rangle , \end{aligned}$$

(B.14)

where we replace the transverse gluon polarization vector by the gluon momentum $(x_2-x_1)n^*$. In Eq. (B.14), we use the Fourier transformations for the quark and gluon fields. $a^+$ and $b^-$ denote the gluon creation and quark annihilation operators, respectively.

In a similar manner, we consider the second diagram contribution of Fig. 5. Before factorization, we have

$$\begin{aligned} \mathcal{B}(\text {dia.2})= & {} \bar{u}(k)\hat{\epsilon }^\perp S(k_1) \int (\mathrm{d}^4\ell ) \hat{\ell }\,t^b\,t^a\, u(k_1+\ell )\nonumber \\&\times \langle P_X| a^+(\ell ) b^-(k_1+\ell )|P\rangle . \end{aligned}$$

(B.15)

Having applied the factorization procedure, we derive the following expression:

$$\begin{aligned} \mathcal{B}(\text {dia.2})= & {} \bar{u}(k)\int \mathrm{d}x_2\hat{\epsilon }^\perp \gamma ^-\,\gamma ^+ \,t^b\,t^a\, u(x_2n^*)\nonumber \\&\times \langle P_X| a^+\big ((x_2-x_1)n^*\big ) b^-(x_1n^*) |P\rangle . \end{aligned}$$

(B.16)

Analyzing Eqs. (B.14) and (B.16), one can see that in order to form the color commutator combination we have to insist on the “external” conditions which actually emanate from the presence of gluon poles. Indeed, if the gluon poles are present, the amplitude $\mathcal{B}(\text {dia.1})$ is accompanied by the factor of $i\pi \delta (x_2-x_1)$. At the same time, the amplitude $\mathcal{B}(\text {dia.2})$ has the factor of $-i\pi \delta (x_2-x_1)$ according to the FSI and ISI prescriptions; see (48).

Thus, to check the QCD gauge invariance, the case of the “perturbative” Compton amplitude with the physical gluons in the initial and final states does not need the external condition for the presence of gluon poles. It is sufficient to use only the momentum conservation, $k_1+k_2=\ell +k$, and the equations of motion for the initial and final quarks. At the same time, in order to demonstrate the QCD gauge invariance for the case represented in Fig. 5 where one of the gluon momenta belongs to the loop integration, the existence of the gluon poles with the corresponding FSI and ISI prescriptions must be included.