1 Introduction

Modified \(f(R)\) gravity represents a possible alternative to Einstein’s theory of general relativity which has received increased attention in the last decade. It is based on a generalization of the Einstein field equations that comes as a result of replacing the Ricci scalar curvature, \(R\), with an arbitrary function of the scalar curvature, \(f(R)\), in the gravitational Lagrangian density. One of the main reasons for increased interest in modified gravity theories comes from the possibility of explaining accelerating expansion of the universe, which has basically been confirmed by observations from type Ia supernovae [1–3], but also from other cosmological observations such as those from large scale structure studies [4], and cosmic microwave background radiation [5]. An important feature of \(f(R)\) gravity is that in its framework, unlike in \(\Lambda \) CDM cosmology based on the standard general relativity, there is no need for postulating dark energy or introducing any kind of new scalar or spinor field to explain the accelerated expansion [6, 7]. The action for \(f(R)\) theories is given by

$$\begin{aligned} S=\frac{1}{2k} \int \sqrt{-g}f(R) \mathrm{d}^{4}x + S_{\mathrm{MAT}}, \end{aligned}$$
(1)

where \(k=8 \pi G\), \(g\) is a determinant of the metric, and \(S_{\mathrm{MAT}}\) is the matter action. Depending on the assumptions taken in the variational procedure starting from (1) we can make a distinction between the metric, the Palatini, and the metric-affine formalism [8, 9]. In the metric formalism we proceed from the assumption that the connection is dependent on the metric, namely that it is given by the Christoffel connection. In the Palatini formalism the connection is treated independent of the metric and it is also assumed that the matter part of the action is not dependent on the connection. Finally, in the metric-affine formalism the matter part of the action now depends on the connection which is metric independent. In this work we will use the metric approach which is the simplest of the above mentioned and also usually used in literature. Using this approach and varying the action (1) with respect to the metric we obtain the following modified field equations:

$$\begin{aligned} R_{\mu \nu }f_{R}(R) - \frac{1}{2} g_{\mu \nu }f(R)-(\nabla _{\mu }\nabla _{\nu }- g_{\mu \nu }\square )f_{R}(R) = k T_{\mu \nu } , \end{aligned}$$
(2)

where

$$\begin{aligned} T_{\mu \nu }=\frac{-2}{\sqrt{-g}} \frac{\delta S_{\mathrm{MAT}}}{\delta g^{\mu \nu }} , \end{aligned}$$
(3)

\(f_{R}=\mathrm{d}f(R)/\mathrm{d}R\), and we will use an analogous notation for higher derivatives of \(f(R)\). Adopting the standard definition: \(G_{\mu \nu }=R_{\mu \nu } - 1/2 Rg_{\mu \nu }\), and after some mathematical manipulations, we can obtain the following equation for the Einstein tensor from (2):

$$\begin{aligned} G_{\mu \nu }= & {} \frac{1}{f_{R}}\left\{ f_{RR}\nabla _{\mu }\nabla _{\nu }R + f_{RRR}(\nabla _{\mu }R)(\nabla _{\nu }R) \right. \nonumber \\&-\left. \frac{g_{\mu \nu }}{6}(R f_{R}+ f + 16 \pi GT)+ 8 \pi G T_{\mu \nu }\right\} , \end{aligned}$$
(4)

where \(T\) is the trace of the stress-energy tensor. In this work we have analyzed wormhole solutions in the framework of viable metric \(f(R)\) gravity models which do not violate standard energy conditions. Wormholes are hypothetical tunnels with a throat that connects two asymptotically flat regions of spacetime. In Einstein’s general relativity, a construction of a wormhole is possible only by the use of exotic matter i.e. matter that violates the usual energy conditions [10–12]. The matter threading the wormhole is usually described by the perfect anisotropic fluid \(T_{\mu \nu }=\mathrm{diag}(\rho ,p_{r},p_{t},p_{t})\). It can be shown that the existence of a wormhole in general relativity implies the condition \(\rho + p_{r}<0\) and according to [10] we shall call the material with this property exotic. This violates the weak energy condition (WEC), which is given by \(T_{\mu \nu }k^{\mu }k^{\nu }\ge 0\) for any timelike vector \(k^{\mu }\) [13]. The WEC expresses constraints on a possible matter behavior in order to guarantee some usual properties, such as positive energy density. On the other hand, it was reported that a static spherically symmetric wormhole can be supported by phantom energy [14]. The general question of the WEC violation in modified gravity still remains open [15]. It was shown in [16] that, in modified gravity with the field equations of the form

$$\begin{aligned} g_{1}(\psi ^{i})(G_{\mu \nu } + H_{\mu \nu }) - g_{2}(\psi ^{j})T_{\mu \nu }=k T_{\mu \nu }, \end{aligned}$$
(5)

where \(H_{\mu \nu }\) is an additional geometrical structure, \(g_{i}(\psi ^{j})\) are multiplicative factors, and \(\psi ^{j}\) are the curvature invariants of the gravitational field, normal matter threading the wormhole can satisfy the WEC if it fulfills the following relationship:

$$\begin{aligned} \frac{g_{1}(\psi ^{i})}{k+g_{2}(\psi ^{j})}(G_{\mu \nu } + H_{\mu \nu })k^{\mu } k^{\nu } \ge 0 . \end{aligned}$$
(6)

In modified \(f(R)\) theories of gravity, wormholes can be supported by ordinary matter [17–19]. Therefore, while we are interested in WEC non-violation we are exploring solutions that satisfy \(\rho \ge 0\) and \(\rho + p_{r}\ge 0\) [17]. Our aim is to analyze, without any additional assumptions, possible wormhole solutions in different viable recently proposed \(f(R)\) models that do not imply the existence of exotic material. In Sect. 2. we present the wormhole geometry and effective field equations, and we derive suitable expressions for the WEC non-violation near the throat. In Sect. 3. we present and analyze some specific solutions in different models. The high curvature regime is considered in Sect. 4. We draw conclusions in Sect. 5.

2 Wormholes in \(f(R)\) gravity

The geometry of a static, spherical symmetric wormhole is given by

$$\begin{aligned} \mathrm{d}s^{2}=-e^{2\varphi (r)} \mathrm{d}t^{2}+\frac{1}{1-\frac{b(r)}{r}}\mathrm{d}r^{2}+r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \mathrm{d}\phi ^{2}), \end{aligned}$$
(7)

where \(\varphi (r)\) is the redshift function and \(b(r)\) is a shape function [10]. The functions \(\varphi (r)\) and \(b(r)\) are arbitrary functions of the radial coordinate \(r\), which nonmonotonically decreases from infinity to a minimal value \(r_{0}\) in the throat and increases to infinity. For the throat position \(r=r_{0} \Rightarrow b(r_{0}) = r_{0}\) the metric tensor component is singular. Nevertheless, the proper distance must be well behaved, from which the following integral must be real and regular outside the throat [10]:

$$\begin{aligned} l(r)=\pm \int ^{r}_{r_{0}}\frac{\mathrm{d}r}{\sqrt{1-b(r)/r}}, \end{aligned}$$
(8)

from which follows the condition:

$$\begin{aligned} 1-b(r)/r\ge 0 . \end{aligned}$$
(9)

So, far from the throat in both radial directions space must be asymptotically flat which implies the condition \( b(r)/r\rightarrow 0 \) as \( l\rightarrow \pm \infty \) [10]. One of the fundamental wormhole properties is that by definition \(b(r)\) must fulfill the flaring-out condition at or near the throat: \((b(r)-b(r)'r)/b^{2}>0\) [10], where \(b'(r)=\mathrm{d}b/\mathrm{d}r\) (in further text prime denotes a derivative with respect to the argument of a function). The second condition which we impose is practical: we demand that a wormhole must be traversable which means the absence of horizons. So \(\varphi (r)\) must be finite everywhere. Using standard mathematical procedure from (7) we obtain the Ricci curvature scalar:

$$\begin{aligned} R= & {} -\frac{2}{r^{2}}\left[ \left( \varphi (r)''r^{2}+2{\varphi (r)'}^{2}r^{2}\right) \left( 1-\frac{b(r)}{r}\right) \right. \nonumber \\&-\frac{\varphi (r)'}{2}(b(r)'r-b(r)) -{\varphi (r)'}^{2}r^{2}\left( 1-\frac{b(r)}{r}\right) \nonumber \\&+\left. 2\varphi (r)'r\left( 1-\frac{b(r)}{r}\right) -r\left( \frac{b(r)'}{r}-\frac{b(r)}{r^{2}}\right) -\frac{b(r)}{r}\right] .\nonumber \\ \end{aligned}$$
(10)

While studying wormholes in \(f(R)\) modified theories of gravity, in order to simplify equations, it is common to place an additional condition on redshift function \(\varphi (r)\) to be constant [17, 20, 21]. This condition on \(\varphi (r)\), which is assumed without any physical reason, is not justified because the fundamental parameters of a wormhole should not be restricted in such an artificial way. Moreover, wormhole solutions of modified Einstein’s equations and the WEC violation will in some cases critically depend on \(\varphi (r)\). Matter is described by the stress-energy tensor of the anisotropic perfect fluid:

$$\begin{aligned} T_{\mu \nu }=(\rho + p_{t})U_{\mu }U_{\nu } + p_{t}g_{\mu \nu } + (p_{r} - p_{t})\chi _{\mu }\chi _{\nu }, \end{aligned}$$
(11)

where \(U\) is a four-velocity, \(\rho \) the energy density, \(p_{t}\) and \(p_{r}\) are transversal and radial pressure, respectively, and \(\chi ^{\mu }= \sqrt{1-b(r)/r}\delta ^{\mu }_{r}\). In (1) we select \(k=1\) for simplicity, and from (4) we obtain modified Einstein’s equations for the wormhole geometry

$$\begin{aligned} \frac{b'(r)f_{R}}{r^{2}}= & {} - f_{RR}\left( 1-\frac{b(r)}{r}\right) R'(r)\varphi '(r)+\frac{1}{6}(R(r)f_{R} + f) \nonumber \\&+ \frac{1}{3}(2\rho + 2p_{t} + p_{r}), \end{aligned}$$
(12)
$$\begin{aligned}&\frac{-b(r)+ 2r^{2}\varphi '(r)(1-b(r)/r)}{r^{3}}f_{R}\nonumber \\&\quad = f_{RR} \left[ R''(r)\left( 1-\frac{b(r)}{r}\right) + \frac{R'(r)}{2}\left( \frac{b(r)}{r^{2}} - \frac{b'(r)}{r}\right) \right] \nonumber \\&\quad \quad +f_{RRR}R(r)^{'2}\left( 1-\frac{b(r)}{r}\right) - \frac{1}{6}(R(r)f_{R}+f) \nonumber \\&\quad \quad + \frac{1}{3}(\rho + 2p_{r} - 2p_{t}), \end{aligned}$$
(13)
$$\begin{aligned}&\left( 1-\frac{b(r)}{r}\right) \left( \varphi ''(r) - \frac{b'(r)r - b}{2r(r-b)}\varphi '(r) + \varphi '(r)^{2}\right. \nonumber \\&\quad \quad + \left. \frac{\varphi '(r)}{r} -\frac{b'(r)r - b}{2r^{2}(r-b)}\right) f_{R} \nonumber \\&\quad = \frac{f_{RR}}{r}\left( 1-\frac{b(r)}{r}\right) R'(r)- \frac{1}{6}(R(r)f_{R}+f)\nonumber \\&\quad \quad + \frac{1}{3}(\rho - p_{r} + p_{t}). \end{aligned}$$
(14)

Note that the field equations (12–14) are fourth order nonlinear differential equations in \(\varphi (r)\) and \(b(r)\). However, Eqs. (12–14) at the same time represent the system of algebraic equations for the stress-energy tensor components, which, despite the complexity, have analytic solutions. In our work in specific models of modified \(f(R)\) gravity we consider solutions for the components of the stress-energy tensor by exploring different redshift, \(\varphi (r)\), and shape functions, \(b(r)\). From the field equations (12–14) we can derive a specific form of the WEC for wormhole solutions in \(f(R)\) gravity

$$\begin{aligned} \rho= & {} \frac{1}{2 r^{2}} \left[ 2f_{RRR}{R'}^{2}(r)r(b(r)-r) +f_{RR}(2R''(r)r((b(r)-r)\right. \nonumber \\&+\left. R'(r)(3b(r)+b'(r)r-4r)) + f_{R}(4r(r-b(r))({\varphi }''(r)\right. \nonumber \\&+\left. {\varphi '}^{2}(r)) - 2b'(r)(1+\varphi '(r)) + 2\varphi '(r) (4r-3b(r))\right. \nonumber \\&+\left. r^{2}R(r))+r^{2}f(R)\right] \ge 0, \end{aligned}$$
(15)
$$\begin{aligned} \rho +p_{r}= & {} \frac{1}{ r^{3}} \left[ f_{RRR}{R'}^{2}(r)r^{2}(b(r)-r) \right. \nonumber \\&+\left. f_{RR}(r^{2}R''(r)(b(r)-r) -R'(r) r^{2}\varphi '(r)(b(r)-r)\right. \nonumber \\&+ \left. \frac{R'(r)}{2}r(b'(r)r-b(r))+f_{R}((b'(r)r-b(r))\right. \nonumber \\&-\left. 2\varphi '(r) r(b(r)-r)) \right] \ge 0, \end{aligned}$$
(16)
$$\begin{aligned} \rho +p_{t}= & {} \frac{1}{ r^{2}} \left[ \left[ \frac{b'(r)r+b(r)}{2r} - (b(r)-r)(r\varphi ''(r)\right. \right. \nonumber \\&+\left. \left. r {\varphi '}^{2}(r)+\varphi '(r)) -\frac{b'(r)r-b(r)}{2}\varphi '(r)\right] f_{R}\right. \nonumber \\&+\left. f_{RR} R'(r) (b(r)-r) (1-r\varphi '(r)) \right] \ge 0. \end{aligned}$$
(17)

We require that the matter threading the wormhole satisfies WEC, so we demand that inequalities (15–17) are fulfilled. Since in Einstein’s general relativity, which corresponds to \(f(R)=R\), this is not possible, higher curvature terms in the action support wormhole geometries. We can see that explicit analysis of Eqs. (15–17) is extremely difficult, and that for a specific wormhole geometry WEC violation can critically depend on the redshift functions \(\varphi (r)\) and its derivatives. As an important and interesting case we can consider Eqs. (16) and (17) near the throat. This approach simplifies the problem considerably. Near the throat \(b(r)\simeq r_{0}\) and the Eqs. (16) and (17) become

$$\begin{aligned} \rho + p_{r}= & {} \frac{b'(r)r-b(r)}{ 2r^{3}}[f_{RR}R'(r)r+2f_{R}]\ge 0. \end{aligned}$$
(18)
$$\begin{aligned} \rho + p_{t}= & {} \frac{f_{R}}{r^{2}} \left[ \frac{b'(r)r+b(r)}{ 2r}- \frac{b'(r)r-b(r)}{ 2}\varphi '(r) \right] \ge 0.\nonumber \\ \end{aligned}$$
(19)

From the flaring-out condition we must have \(b'(r)r-b(r)<0\), so for Eq. (18) we simply obtain

$$\begin{aligned} f_{RR}R'(r)r+2f_{R}\le 0 \quad \text {near the throat}. \end{aligned}$$
(20)

This condition is, due to its simplicity, particularly suitable for analyzing the influence of modifying the theory of gravity on the question of the WEC violation. It is obvious that this condition cannot be fulfilled for every choice of \(f(R)\). For instance, if we take \(f(R)=R\) this condition is not satisfied and this corresponds to the need for exotic matter in Einstein’s relativity. As we will show in the later part of our work, for analyzed models we typically have \(f_{R}<0\) near the throat, and from (19) we obtain the condition

$$\begin{aligned} b'(r) \le \frac{b(r)(1+r \varphi '(r))}{ r^{2}\varphi '(r) - r}. \end{aligned}$$
(21)

If \(\varphi (r)\) is taken to be differentiable and continuous function on the interval \([r_{0}, \infty \rangle \) and \(\frac{(1+r \varphi '(r))}{ r^{2}\varphi '(r) - r}\) continuous on the same interval, then according to the Gronwall–Bellman inequality we have

$$\begin{aligned} b(r) \le b(r_{0})\exp \left( \int _{r_{0}}^{r} \frac{1+z\varphi '(z)}{z(z\varphi '(r)-1)} \mathrm{d}z \right) . \end{aligned}$$
(22)

From this expression we can see the importance of \(\varphi (r)\): for a given redshift function we can solve the integral (22) and determine the function that bounds \(b(r)\) near the throat. Taking this bounding function as a critical case we can determine Ricci scalar and check whether (18) is satisfied in the concrete \(f(R)\) model. Let us consider a specific example \(\varphi (r)=\mathrm{constant}\) for simplicity. Bounding shape function is then

$$\begin{aligned} b(r)_{\mathrm{critical}}= b(r_{0})\frac{r_{0}}{r}. \end{aligned}$$
(23)

Then calculating the Ricci scalar and its derivative, from (18) we obtain the condition

$$\begin{aligned} \frac{f_{R}}{f_{RR}} \le - \frac{4 b(r_{0})r_{0}}{r^{4}}, \end{aligned}$$
(24)

which depends only on a specific \(f(R)\) model when the constants \(b(r_{0})\) and \(r_{0}\) are given.

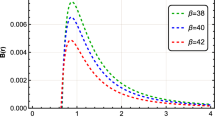
In the next section our approach will be to find specific solutions of Eqs. (12–14) for a given wormhole geometry and then check whether the WEC is satisfied or not, rather than analyze Eqs. (15–17). We will focus on the question of condition (16) violation for the specific \(f(R)\) models, since it is this part of the WEC that is necessary violated near the throat in Einstein’s general theory of relativity, and it was used as a definition for exotic matter in [10]. For the simple choices of \(b(r)\) and \(\varphi (r)\) in the considered models, \(\rho + p_{t}\) is typically violated somewhere away from the throat, as shown in Fig. 1 for all models. This should not be of primary concern, since it is the throat connecting two asymptotically flat regions that is of the main interest, and one can always cut off the solution at some \(r_{c}\) away from the throat and connect it with other asymptotically flat solution of modified Einstein’s equations in that region. This would physically correspond to a wormhole in a spacetime in which another energy-momentum distribution starts to dominate for \(r\ge r_{c}\).

Fig. 1
figure 1

\(\rho +p_{t}\) for all models, respectively, MJWQ model: \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), and parameters \(\beta =2\), \(R_{*}=2\), the Starobinsky model: \(b(r)=r_{0}\ln {r}/r_{0}+r_{0}\), \(\varphi (r)=\sqrt{r_{0}/r}\) and parameters \(q=2\), \(\lambda =1\), the exponential gravity model: \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), and parameters \(\lambda =2\), \(R_{*}=2\), the Tsujikawa model: \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), and parameters \(\mu =2\) \(R_{*}=1\), where \(x=r/r_{0}\)

Full size image

3 Specific models and solutions

In some works which analyze wormholes in the context of \(f(R)\) gravity [17, 20] \(f(R)\) is usually treated as an unknown function, which can be derived from modified field equations, or it is considered to have some simple convenient shape. We prefer the approach in which the \(f(R)\) functions are taken as predetermined characteristic of the theory. In fact, due to the highly hypothetical nature of a wormhole, which is at the moment far away from any empirical observation, we cannot impose conditions on \(f(R)\) in a manner stated above. Therefore, the form of \(f(R)\) should be consistent with observations for the Solar System and cosmological evolution, so we analyze wormhole solutions in several viable models of \(f(R)\) gravity [22–26]:

  • MJWQ model [27]

    $$\begin{aligned} f(R)=R- \beta R_{*}\ln \left( 1+\frac{R}{R_{*}}\right) , \end{aligned}$$
    (25)

    where \(\beta \) and \(R_{*}\) are free positive parameters of the model.

  • Starobinsky model [28–33]

    $$\begin{aligned} f(R)=R + \lambda R_{*}\left[ \left( 1+ \left( \frac{R^{2}}{R_{*}^{2}}\right) \right) ^{- q}-1\right] , \end{aligned}$$
    (26)

    with three free positive parameters \(\lambda \), \(R_{*}\), and \(q\).

  • Exponential gravity model [34, 35]

    $$\begin{aligned} f(R)= R - R_{*}\lambda (1 - e^{-\tilde{R}}), \end{aligned}$$
    (27)

    where \(\tilde{R}=R/R_{*}\), with \(\lambda \) and \(R_{*}\) as free positive parameters of the model.

  • Tsujikawa model [30, 36]

    $$\begin{aligned} f(R)=R-\mu R_{*} \tanh \left( \frac{R}{R_{*}}\right) \end{aligned}$$
    (28)

    where \(\mu \) and \(R_{*}\) are free positive parameters of the model.

In all models \(R_{*}=\sigma H_{0}^{2}\), where \(\sigma \) is some dimensionless parameter and \(H_{0}\) is the current value of the Hubble parameter, which is taken to be \(H_{0}=1\).

It was shown in [37, 38] that for a scalar-tensor theory of gravity, formulated in the Jordan frame with the field Lagrangian

$$\begin{aligned} L=\frac{1}{2}\left[ f(\Phi )R + h(\Phi )g^{\mu \nu }\Phi _{, \mu } \Phi _{, \nu } - 2U(\Phi )\right] , \end{aligned}$$
(29)

no static wormholes that satisfy the null energy condition can be formed, as long as \(f(\Phi )\) is everywhere positive and also

$$\begin{aligned} f(\Phi )h(\Phi )+\frac{3}{2}\left( \frac{\mathrm{d} f}{\mathrm{d} \Phi }\right) ^{2} >0, \end{aligned}$$
(30)

where \(f\), \(h\), and \(U\) are arbitrary functions. For \(f(R)\) gravity we have \(f(\Phi )=f_{R}\), \(h=0\), and \(2U(\Phi )=Rf_{R} - f(R)\). Therefore, two conditions for wormholes non-existence in \(f(R)\) gravity read \(f_{R} >0\) and \(f_{RR}>0\). As can be seen from Fig. 2 the considered models have regions with \(f_{R}<0\) and therefore violate the non-existence theorem conditions. However, this opens the question of the stability of solutions under non-static perturbations which should be considered in the further work.

Fig. 2
figure 2

The MJWQ model: \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), and parameters \(\beta =2\), \(R_{*}=2\), the Starobinsky model: \(b(r)=r_{0}\ln {r}/r_{0}+r_{0}\), \(\varphi (r)=\sqrt{r_{0}/r}\), and parameters \(q=2\), \(\lambda =1\), the exponential gravity model: \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), and parameters \(\lambda =2\), \(R_{*}=2\), the Tsujikawa model: \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), and parameters \(\mu =2\) \(R_{*}=1\), where \(x=r/r_{0}\)

Full size image

3.1 MJWQ model

In MJWQ model (25) we solve field equations (12–14) to obtain components of the stress-energy tensor and check if the conditions \(\rho \ge 0\) and \(\rho +p_{r}\ge 0\) are satisfied. We consider specific redshift and shape functions given by \(\varphi (r)=\ln (r_{0}/r+1)\) and \(b(r)=r_{0}\sqrt{r_{0}/r}\). The parameters of the model, \(\beta \) and \(R_{*}\), are taken to be close to the values proposed in [22]. Above mentioned solutions are depicted in Figs. 3 and 4. A choice of the free parameters in the \(f(R)\) model plays a significant role in the question of the WEC violation. For all shown combinations of parameters both conditions are satisfied, except the case \(\beta =2\) and \(R_{*}=1\), which was proposed in [22].

Fig. 3
figure 3

Energy density, \(\rho \), in the MJWQ model for the specific choice of \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), where \(x=r/r_{0}\)

Full size image
Fig. 4
figure 4

The non-exotic material condition, \(\rho +p_{r}\), in the MJWQ model for the specific choice of \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), where \(x=r/r_{0}\)

Full size image

3.2 Starobinsky model

Let us consider specific functions \(b(r)=r_{0}\ln {r}/r_{0}+r_{0}\), \(\varphi (r)=\sqrt{r_{0}/r}\). As in [22] we choose \(R_{*}=4.17\) with \(\lambda \) and \(q\) close to the values \(\lambda =1\), \(q=2\). The solutions are depicted in Figs. 5 and 6. We see that every combination of parameters implies the need for exotic matter. Moreover, for every considered combination of simple shape and redshift functions we did not find non-exotic matter solutions in the Starobinsky model.

Fig. 5
figure 5

Energy density, \(\rho \), in the Starobinsky model for the specific choice of \(b(r)=r_{0}\ln {r}/r_{0}+r_{0}\), \(\varphi (r)=\sqrt{r_{0}/r}\), where \(x=r/r_{0}\)

Full size image
Fig. 6
figure 6

The non-exotic material condition, \(\rho +p_{r}\), in the Starobinsky model for the specific choice of \(b(r)=r_{0}\ln {r}/r_{0}+r_{0}\), \(\varphi (r)=\sqrt{r_{0}/r}\), where \(x=r/r_{0}\)

Full size image

3.3 Exponential gravity model

We take the shape and the redshift functions previously considered in the MJWQ model with \(\lambda \) and \(R_{*}\) close to the values in [22]. Solutions are presented in Figs. 7 and 8. For all combinations the conditions are satisfied except for the choice \(\lambda =2\) and \(R_{*}=1\).

Fig. 7
figure 7

Energy density, \(\rho \), in the exponential gravity model for the specific choice of \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), where \(x=r/r_{0}\)

Full size image
Fig. 8
figure 8

The non-exotic material condition, \(\rho +p_{r}\), in the exponential gravity model for the specific choice of \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), where \(x=r/r_{0}\)

Full size image

3.4 Tsujikawa model

Finally, the results for the Tsujikawa model are plotted in Figs. 9 and 10. For comparison we choose the same shape and redshift functions as in the MJWQ and the exponential gravity model. For values smaller than \(\mu =2\) and \(R_{*}=1\) the model requires exotic matter.

Fig. 9
figure 9

Energy density, \(\rho \), in the Tsujikawa model for the specific choice of \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), where \(x=r/r_{0}\)

Full size image
Fig. 10
figure 10

The non-exotic material condition, \(\rho +p_{r}\), in the Tsujikawa model for the specific choice of \(b(r)=r_{0}\sqrt{r_{0}/r}\), \(\varphi (r)=\ln (r_{0}/r+1)\), where \(x=r/r_{0}\)

Full size image

4 High curvature regime

It is interesting to consider the high curvature limit in the problem of wormholes in viable \(f(R)\) modified theories of gravity. Specific \(f(R)\) models which are considered in this work should reproduce realistic scenarios of cosmological evolution based on the accelerated expansion of the universe. Cosmological models based on viable \(f(R)\) theories asymptotically approach the de-Sitter solution which in Einstein’s general relativity corresponds to an empty space filled with the positive cosmological constant [39]. In accordance with this demand all considered models share the same mathematical property that in the high curvature limit they have the following form:

$$\begin{aligned} f(R)\approx R-\lambda R_{*}, \end{aligned}$$
(31)

so the models lead to the effective cosmological constant \(\lambda R_{*}/2\), as can be seen by applying (31 to 2) and using the standard definition of the cosmological constant in Einstein’s field equations. Therefore the high curvature regime is interesting because we have an interplay of cosmological features of the \(f(R)\) models and wormhole solutions. We expect to have the high curvature limit in the vicinity of the throat for a suitable choice of \(b(r)\) and \(\varphi (r)\) which will lead to \(R(r)\gg R_{*}\). By rewriting Einstein’s field equations (12–14), with (10) and (31), we can easily obtain the solutions for the stress-energy tensor components in the high curvature limit,

$$\begin{aligned} \rho= & {} -\frac{-2b'(r)+\lambda R_{*}r^{2}}{2r^{2}},\end{aligned}$$
(32)
$$\begin{aligned} p_{r}= & {} -\frac{2 b(r) + 4 b(r) \varphi '(r) r - 4 \varphi '(r) r^2 -\lambda R_{*} r^3}{2r^{3}},\end{aligned}$$
(33)
$$\begin{aligned} p_{t}= & {} \varphi ''(r) + \varphi (r)^2 + \frac{\lambda R_{*}}{2} + \frac{b(r)}{2 r^3} - \frac{b'(r)}{2 r^{2}} \nonumber \\&- \frac{b(r)\varphi '(r)}{ 2 r^2} - \frac{b(r)\varphi ''(r)}{r} + \frac{\varphi '(r)}{r} \nonumber \\&- \frac{b'(r)\varphi '(r)}{ 2 r} - \frac{b(r)\varphi '(r)^{2}}{r}. \end{aligned}$$
(34)

It can be seen that these equations are equal to the ones presented in [10] with addition of an effective cosmological constant, as should be expected. By inspecting (20) it is apparent that the WEC is violated near the throat in the high curvature regime. Since all viable \(f(R)\) models share the same asymptotic behavior described by (31) one can question the critical \(R(r)\) value for every point near the throat, in a specific \(f(R)\) model. By critical value we mean the highest possible \(R(r)\) value for which WEC is satisfied at a specific point in space. Let us consider solutions, \(R_{\mathrm{critical}}(r)\), of the following equation, which can be obtained from (20):

$$\begin{aligned} f_{RR}R_{\mathrm{critical}}'(r)r+2f_{R}=0 ~~~\text {near the throat}, \end{aligned}$$
(35)

as well as solutions, \(\bar{R}\), of the WEC violation inequality

$$\begin{aligned} f_{RR}\bar{R}'(r)r+2f_{R}>0. \end{aligned}$$
(36)

From the theory of differential inequalities follows

$$\begin{aligned} \bar{R}(r)>R_{\mathrm{critical}}(r), \end{aligned}$$
(37)

in the interval near the throat \(r_{0}<r<r_{1}\), where \(\bar{R}(r_{0})=R_{\mathrm{critical}}(r_{0})\). Therefore, values of \(R_{\mathrm{critical}}\) correspond to the critical values of the Ricci scalar in the above mentioned sense. We can solve Eq. (35) and obtain \(R_{\mathrm{critical}}\) in different models of \(f(R)\) gravity. For instance in the MJWQ model we get

$$\begin{aligned} R_{\mathrm{critical}}(r)=\frac{\left( \frac{r^{2}}{r_{0}^{2}}\right) ^{2}-\frac{1-R_{0}}{1+R_{0}}}{\left( \frac{r^{2}}{r_{0}^{2}}\right) ^{2}+\frac{1-R_{0}}{1+R_{0}}}, \end{aligned}$$
(38)

where \(R_{*}=1\), \(\beta =2\), \(R(r_{0})=R_{0}\). In exponential gravity for fixed parameters \(q=2\), \(\lambda =2\) we obtain

$$\begin{aligned} R_{\mathrm{critical}}(r)=\ln \frac{4r^{2}}{(c+r^{2})^{2}}, \end{aligned}$$
(39)

with \(c=\frac{2r_{0}^{2}}{e^{R_{0}/2}}-r_{0}^{2}\). In this way it is possible to considerably simplify the analysis of the wormhole WEC violation in \(f(R)\) theories of gravity. For a given \(R(r)\) one can compare its values near the throat with values of \(R_{\mathrm{critical}}(r)\) in a concrete \(f(R)\) model and, using (37) and (36), check whether WEC is violated. Of course, non-violation of (20) is necessary, but not sufficient for WEC non-violation.

5 Conclusions

We have examined possible wormhole solutions in four viable recently proposed \(f(R)\) models, namely: the MJWQ model, the Starobinsky model, the exponential gravity model, and the Tsujikawa model. In all models apart from the Starobinsky model we have found solutions that do not require exotic matter. Our solutions do not presume any additional assumption on the redshift function, \(\varphi (r)\). For the given functions \(\varphi (r)\) and \(b(r)\) we can see that for the above cases the character of the solutions in the MJWQ, exponential gravity and Tsujikawa model depends more strongly on the choice of the free parameters than on the choice of a specific model. It is also possible to satisfy non-exotic matter conditions with other simple choices of \(\varphi (r)\) and \(b(r)\) for each model. For instance, \(b(r)=r_{0}e^{(1-r/ r_{0})}\), \(b(r)=r_{0}^{2}/r\), \(\varphi (r)=1/r\), etc.

A simple inequality for the WEC violation near the throat is derived, which we demonstrate to be particularly suitable for analyzing the influence of modifying theory of gravity as regards the question of the WEC violation. We have shown that all viable \(f(R)\) models must share the same mathematical form in the high curvature regime and that in this limit the WEC is necessarily violated. The question of critical values of the Ricci scalar, i.e. the highest possible values of the Ricci scalar for which the WEC is not violated near the throat, is considered. We have calculated functions of the Ricci scalar that give these critical values for several models. Following this approach, and comparing values of some arbitrary Ricci scalar near the throat with critical values, it is straightforward to check whether the necessary condition of the WEC non-violation is satisfied. While in some previous works WEC violation was analyzed in some simple \(f(R)\) frameworks, we have considered viable and realistic models, and showed that wormholes that do not demand exotic matter can be constructed in them. In further work it would be interesting to analyze the stability of the solutions, as well as solutions in non-spherically symmetric wormholes and wormholes supported by scalar and gauge fields instead of perfect anisotropic fluid, in \(f(R)\) theories of gravity.