Can static regular black holes form from gravitational collapse?

Abstract

Starting from the Oppenheimer–Snyder model, we know how in classical general relativity the gravitational collapse of matter forms a black hole with a central spacetime singularity. It is widely believed that the singularity must be removed by quantum-gravity effects. Some static quantum-inspired singularity-free black hole solutions have been proposed in the literature, but when one considers simple examples of gravitational collapse the classical singularity is replaced by a bounce, after which the collapsing matter expands for ever. We may expect three possible explanations: (i) the static regular black hole solutions are not physical, in the sense that they cannot be realized in Nature, (ii) the final product of the collapse is not unique, but it depends on the initial conditions, or (iii) boundary effects play an important role and our simple models miss important physics. In the latter case, after proper adjustment, the bouncing solution would approach the static one. We argue that the “correct answer” may be related to the appearance of a ghost state in de Sitter spacetimes with super Planckian mass. Our black holes have indeed a de Sitter core and the ghost would make these configurations unstable. Therefore we believe that these black hole static solutions represent the transient phase of a gravitational collapse but never survive as asymptotic states.

1 Introduction

In classical general relativity, under the main assumptions of the validity of the strong energy condition and of the existence of global hyperbolicity, the collapse of matter inevitable produces a singularity of the spacetime [1, 2]. At a singularity, predictability is lost and standard physics breaks down. According to the weak cosmic censorship conjecture, spacetime singularities formed from collapse must be hidden behind an event horizon and the final product of the collapse must be a black hole [3]. In 4-dimensional general relativity, the only uncharged black hole solution is the Kerr metric [4, 5], which reduces to the Schwarzschild solution in the spherically symmetric case. The Oppenheimer–Snyder model is the simplest fully analytic example of gravitational collapse, describing the contraction of a homogeneous spherically symmetric cloud of dust [6]. It clearly shows how the collapse produces a spacetime singularity and the final product is a Schwarzschild black hole.

In analogy with the appearance of divergent quantities in other classical theories, it is widely believed that spacetime singularities are a symptom of the limitations of classical general relativity, to be removed by quantum-gravity effects. While we do not have yet any robust and reliable theory of quantum gravity, the resolution of spacetime singularities has been investigated in many quantum-gravity inspired models. Very different approaches have studied corrections to the Schwarzschild/Kerr solution, finding black hole metrics in which the curvature invariants are always finite [7–13].¹ In the same spirit, one can study the modifications to the Oppenheimer–Snyder solution and to other models of collapse. In this case, the singularity is replaced by a bounce, after which the cloud starts expanding [14–18]. It is therefore disappointing that the quantum-gravity corrected model of collapse does not reproduce the quantum-gravity corrected black hole solution.

In this paper, we want to investigate this apparent contradictory result. First, we determine both the quantum-gravity corrected static black hole metric and the quantum-gravity corrected homogeneous collapse solution within the same theoretical framework, since the ones reported in the literature come from different models. We find that the problem indeed exists. Second, we try to figure out the possible reason. One possibility is that the static regular black hole spacetimes are ad hoc solutions, but they cannot be created in a collapse and therefore they are physically irrelevant. The collapse always produces an object that bounces. Another possible explanation is that the final product of the collapse depends on the initial conditions. The collapse of a homogeneous cloud creates an object that bounces, while with other initial conditions (not known at present) the final product is a static regular black hole. Lastly, it is possible that the simple homogeneous collapse oversimplifies the model, ingoing and outgoing energy fluxes between the interior and the exterior solutions are important, and, after proper readjustment that seems to be difficult to have under control within an analytic approach, the collapsing model approaches the static regular black hole solution. Our quantum-gravity inspired theories are unitary, super-renormalizable or finite at quantum level, and there are no extra degrees of freedom at perturbative level around flat spacetime. This should rule out the possibility that the explanation of our puzzle is due to the fact that these models may not be consistent descriptions of quantum gravity. However, these theories display a ghost state in de Sitter spacetime when the cosmological constant exceeds the square of the Planck mass. This fact may be responsible for our finding and answers the question in the title of this paper. Our black holes have indeed a de Sitter core with an effective cosmological constant larger than the square of the Planck mass when the black hole mass exceeds the Planck mass. The presence of a ghost makes the solutions unstable and therefore they cannot be the final product of the gravitational collapse.

The content of the paper is as follows. In the next section, we briefly review the classical homogeneous and spherically symmetric collapse model. In Sect. 3, we derive the spherically symmetric black hole solutions in a super-renormalizable and asymptotically free theory of gravity with the family of form factors proposed by Krasnikov [19] and Tomboulis [20]. In Sect. 4, we study the spherically symmetric homogeneous collapse in the same models. Summary and conclusions are in Sect. 5.

2 Black holes and gravitational collapse in classical general relativity

The most general spherically symmetric metric describing a collapsing cloud of matter in comoving coordinates is given by

$$\begin{aligned} \mathrm{d}s^2=-\mathrm{e}^{2\nu }\mathrm{d}t^2+\frac{R'^2}{G}\mathrm{d}r^2+R^2\mathrm{d}\Omega ^2, \end{aligned}$$

(1)

where $\mathrm{d}\Omega ^2$ represents the line element on the unit two-sphere and $\nu$, $R$, and $G$ are functions of $t$ and $r$. The energy-momentum tensor is given by

$$\begin{aligned} T^\mu _\nu =\mathrm{diag}( -\rho (r,t), p_r(r,t), p_\theta (r,t), p_\theta (r,t) ), \end{aligned}$$

(2)

and the Einstein equations reduce to

$$\begin{aligned} \frac{\kappa ^2}{2} \rho&= \frac{F'}{R^2R'}, \end{aligned}$$

(3)

$$\begin{aligned} \frac{\kappa ^2}{2} p_r&= - \frac{\dot{F}}{R^2\dot{R}}, \end{aligned}$$

(4)

$$\begin{aligned} \nu '&= 2 \frac{p_\theta - p_r}{\rho + p_r} \frac{R'}{R} - \frac{p'_r}{\rho + p_r}, \end{aligned}$$

(5)

$$\begin{aligned} \dot{G}&= 2\frac{\nu '}{R'}\dot{R}G, \end{aligned}$$

(6)

where the $'$ denotes a derivative with respect to $r$, and the $\dot{}$ denotes a derivative with respect to $t$. The function $F(r,t)$ is called Misner–Sharp mass and is defined by

$$\begin{aligned} F=R(1-G+\mathrm{e}^{-2\nu }\dot{R}^2). \end{aligned}$$

(7)

The whole system has a gauge degree of freedom that can be fixed by setting the scale at a certain time. One usually sets the area radius $R(r,t)$ to be equal to the comoving radius $r$ at the initial time $t_\mathrm{i}=0$, i.e. $R(r,0)=r$. We can then introduce a scale factor $a$

$$\begin{aligned} R(r,t)=ra, \end{aligned}$$

(8)

which will go from 1, at the initial time, to 0, at the time of the formation of the singularity. The condition to describe collapse is $\dot{a}<0$.

For a homogeneous perfect fluid, $p_r = p_\theta = p(t)$. The simplest case is the gravitational collapse of a cloud of dust, $p=0$, which is the well-known Oppenheimer–Snyder model [6]. From Eq. (3), we see that $F$ is proportional to the amount of matter enclosed within the shell labeled by $r$ at the time $t$. For dust, from Eq. (4) it follows that $F$ is independent of $t$, so there are no inflows and outflows through any spherically symmetric shell of radial coordinate $r$. If $r_\mathrm{b}$ denotes the comoving radial coordinate of the boundary of the cloud, $F(r_\mathrm{b})=2M_\mathrm{Sch}$, where $M_\mathrm{Sch}$ is the Schwarzschild mass of the vacuum exterior. Let us note that in the general case of a perfect fluid this is not true, and for a non-vanishing pressure the homogeneous spherically symmetric interior must be matched with a non-vacuum Vaidya exterior spacetime. Equation (5) reduces to $\nu ' = 0$ and one can always choose the time gauge in such a way that $\nu =0$. From Eq. (6), we find that $G$ is independent of $t$ and we can write $G=1+f(r)$. In the homogeneous marginally bound case (representing particles that fall from infinity with zero initial velocity), $f=0$ and therefore $G=1$.

In the homogeneous spherically symmetric gravitational collapse of a cloud of dust, one finds that the energy density is given by

$$\begin{aligned} \rho (t) = \frac{\rho _0}{a^3}, \end{aligned}$$

(9)

where $\rho _0$ is the energy density at the initial time $t_\mathrm{i} = 0$, and the scale factor is

$$\begin{aligned} a(t) = \left( 1-\frac{\sqrt{3 \rho _0}}{2} t\right) ^{2/3}. \end{aligned}$$

(10)

The model has a strong curvature singularity for $a = 0$, which occurs at the time $t_\mathrm{s} = 2/\sqrt{3\rho _0}$, as can be seen from the divergence of the Kretschmann scalar,

$$\begin{aligned} R_{\mu \nu \rho \sigma } R^{\mu \nu \rho \sigma } =12 \frac{\ddot{a}^2 a^2 + \dot{a}^4}{a^4}. \end{aligned}$$

(11)

The boundary of the cloud collapses along the curve $R(r_\mathrm{b},t)=r_\mathrm{b} a(t)$ and the whole cloud becomes trapped inside the event horizon at the time $t_\mathrm{tr}<t_\mathrm{s}$ for which $R(r_\mathrm{b},t_\mathrm{tr})=2M_\mathrm{Sch}=r_\mathrm{b}^3 \rho _0/3$, so

$$\begin{aligned} t_\mathrm{tr}=t_\mathrm{s} - \frac{4M_\mathrm{Sch}}{3}. \end{aligned}$$

(12)

For $p \ne 0$, the exterior solution is not Schwarzschild, but the Vaidya spacetime, because there is a non-vanishing flux through the boundary $r_\mathrm{b}$ and $F(r_\mathrm{b},t)$ does depend on time. In the radiation case, one finds

$$\begin{aligned} \rho (t)&= \frac{\rho _0}{a^4}, \end{aligned}$$

(13)

$$\begin{aligned} a(t)&= \left( 1-2\sqrt{\frac{\rho _0}{3}}t \right) ^{1/2}, \end{aligned}$$

(14)

where $\rho _0$ is the energy density at the initial time $t_\mathrm{i} = 0$ and the singularity occurs at the time $t_\mathrm{s}=\sqrt{3/\rho _0}/2$. Like in the dust model, the final outcome is a Schwarzschild black hole. For the generic case of a perfect fluid with equation of state $p = \omega \rho$, the scale factor is (for $\omega \ne -1$)

$$\begin{aligned} a(t) = \left( 1 - \frac{t}{t_\mathrm{s}}\right) ^{\frac{2}{3(\omega + 1)}}, \end{aligned}$$

(15)

where $t_\mathrm{s}$ is the time of the formation of the singularity

$$\begin{aligned} t_\mathrm{s} = \frac{2}{(\omega + 1) \sqrt{3\rho _0}}. \end{aligned}$$

(16)

The time of the formation of the event horizon is still given by $R(r_b,t_\mathrm{tr})=F(r_b,t_\mathrm{tr})$ and occurs before the time $t_\mathrm{s}$.

3 Quantum-gravity inspired black holes

We start from the classical Lagrangian of the renormalized theory in [21],

$$\begin{aligned} \mathcal {L}=-\sqrt{-g} \left\{ \frac{1}{\kappa ^2} R - G^{\mu \nu } \frac{V^{-1}(-\Box _\Lambda )-1}{\kappa ^2 \Box _{\Lambda }} R_{\mu \nu } \right\} , \end{aligned}$$

(17)

where $\Box _\Lambda = p^\mu p_\mu /\Lambda ^2$ and we use the signature $(-,+,+,+)$. The main properties of our theoretical framework are discussed in Appendix A, where we show that the theories studied in this paper are unitary, super-renormalizable or finite at the quantum level, and there are no extra degrees of freedom (ghosts or tachyons) in flat spacetime. We note that we are not considering “local higher derivative theories of gravity”, but “weakly nonlocal theories of gravity”. Here by nonlocality we mean that we have an operator with an infinite number of derivatives, while in a local theory the number of these derivatives would be finite. We use the term “weakly” because it is only the whole sum that makes the theory nonlocal. However, the nonlocality is not enough to have a good theory. We need the propagator to be the standard one times an entire function without zeros, singularities or poles in the whole complex plane. In this case, the theory does not have ghosts by construction, because the residue of the propagator at the pole is the same as the one of general relativity. The regularization of the solutions is thus due to the choice of the form factor and to the absence of interactions at high energy or, in other words, to asymptotic freedom. More details can be found in [17]. The equations of motion for the theory up to terms quadratic in the curvature are

$$\begin{aligned} G_{\mu \nu }+O(R^2_{\mu \nu }) = \frac{\kappa ^2}{2} V(-\Box _\Lambda ) T_{\mu \nu }. \end{aligned}$$

(18)

The right hand side can be considered as an effective energy-momentum term, defined by $\mathcal {S}_{\mu \nu }=V(-\Box _\Lambda ) T_{\mu \nu }$. Within this approximation, the left hand side is compatible with the Bianchi identity, so the effective energy-momentum tensor is conserved,

$$\begin{aligned} \nabla ^\mu \mathcal {S}_{\mu \nu }= \nabla ^\mu [ V(-\Box _\Lambda )T_{\mu \nu } ]=0. \end{aligned}$$

(19)

Now we want to solve the field equations for a static and spherically symmetric source. From the static property, the four-velocity is $u^\mu =(u^0, \vec {0})$; that is, only the timelike component is non-zero, and $u^0=(-g_{00})^{-1/2}$. For simplicity, we consider a point source. The $T^0_0$ component is given by $T^0_0=-M \frac{\delta (r)}{4 \pi r^2}=-M \delta ^3(\vec {x})$. Spherical or Cartesian-like coordinates are adopted to make calculations easier. In the spherically symmetric case, the metric is assumed to have the Schwarzschild form,

$$\begin{aligned} \mathrm{d}s^2=-F(r)\mathrm{d}t^2 + \frac{\mathrm{d}r^2}{F(r)} +r^2 \mathrm{d}\Omega ^2 \end{aligned}$$

(20)

where $F(r)$ is

$$\begin{aligned} F(r)=1-\frac{2 m(r)}{r} \end{aligned}$$

(21)

and $m(r)$ is the mass enclosed within the radius $r$.

The effective energy-momentum tensor is defined by

$$\begin{aligned} \mathcal {S}^{\mu }_{\nu }\equiv V(-\Box _\Lambda ) T^{\mu }_{\nu } =\mathrm{diag} ( -\rho ^e, p_r^e, p_\theta ^e, p_\theta ^e ). \end{aligned}$$

(22)

The $\mathcal {S}^0_0$ component can be rewritten as

$$\begin{aligned} \rho ^e(\vec {x})&= V(-\Box _\Lambda ) M \delta ^{(3)} (\vec {x}) \nonumber \\&= M \int \frac{\mathrm{d}^3 k}{(2 \pi )^3} V\left( -\frac{k^2}{\Lambda ^2}\right) \mathrm{e}^{i\vec {k} \cdot \vec {x}} \nonumber \\&= \frac{M}{2\pi ^2} \int _0^\infty k^2 \frac{\mathrm{sin} kr}{kr} V\left( -\frac{k^2}{\Lambda ^2}\right) \mathrm{d} k, \end{aligned}$$

(23)

where $r=| \vec {x} |$. This is the representation for the effective energy density, and, once the form factor is specified, it can be numerically solved to get $\rho ^e(r)$. The radial integral contains the term $\frac{\mathrm{sin} kr}{kr}$. If we expand the sine function, we have

$$\begin{aligned} \rho ^e(r)=\frac{M}{2 \pi ^2} \int _0^\infty k^2 V \left( -\frac{k^2}{\Lambda ^2} \right) \mathrm{d}k+O(r^2). \end{aligned}$$

(24)

Independently of the choice of the form factor $V(z)$, the leading term is a constant, which means that at $r=0$ we will always have a positive effective energy density proportional to the mass $M$ and fully determined by $V(z)$. As long as the convergence velocity of $V(z)$ is larger than $k^{-3}$, we are able to get a finite effective energy density. In classical general relativity, $V(z) = 1$ and the result is not finite.

The covariant conservation and the additional condition $g_{tt}=-g_{rr}^{-1}$ completely determines $\mathcal {S}_{\mu \nu }$. The Einstein equations give

$$\begin{aligned} \frac{\mathrm{d}m}{\mathrm{d}r}&= \frac{\kappa ^2}{4} \rho ^e r^2, \end{aligned}$$

(25)

$$\begin{aligned} \frac{1}{F} \frac{\mathrm{d}F}{\mathrm{d}r}&= \frac{2[m(r)+ \frac{\kappa ^2}{4} p^e_r r^3]}{r[r-2m(r)]}, \end{aligned}$$

(26)

$$\begin{aligned} \frac{\mathrm{d}p^e_r}{\mathrm{d}r}&= -\frac{1}{2F} \frac{\mathrm{d}F}{\mathrm{d}r} (\rho ^e+p^e_r)+\frac{2}{r}(p^e_\theta -p^e_r). \end{aligned}$$

(27)

From Eq. (25), we find the mass enclosed in the radius $r$

$$\begin{aligned} m(r)=\frac{\kappa ^2}{4} \int _0^r \mathrm{d}r' r'^2 \rho ^e(r'). \end{aligned}$$

(28)

At $r=0$, $m=0$, and $F=1$. For $r \rightarrow \infty$, $m$ is a constant and $F(r)\rightarrow 1$. We have thus solutions with two or more horizons. Moreover, at $r=0$ a constant energy density gives a de Sitter spacetime, independently of the choice of the form factor. Here the effective cosmological constant is of order $\kappa ^2 M \Lambda ^3$ and this, as argued at the end of this paper, may be the key ingredient of the answer to our question.

We now consider two specific form factors, proposed, respectively, by Krasnikov [19] and by Tomboulis [20]:

$$\begin{aligned} V(z)&= \mathrm{e}^{-|z|^n}, \end{aligned}$$

(29)

$$\begin{aligned} V(z)&= \mathrm{e}^{-\frac{1}{2} [ \gamma _E +\Gamma (0, p_{\gamma +1} (z)^2) + \mathrm{ln} \, p_{\gamma +1} (z)^2 ]}. \end{aligned}$$

(30)

Here $p_{\gamma +1}(z)$ is a polynomial of order $\gamma +1$. The super-renormalizability of the theory requires $\gamma \ge 3$ and in what follows we will only consider the minimal renormalizable theory with $\gamma =3$. In the low energy limit, $z\equiv -\Box _\Lambda \rightarrow 0$, and to recover general relativity we need $V(z)\rightarrow 1$. So $p_{\gamma +1}(0)=0$. Moreover, we should expect deviations from general relativity when $z\ne 0$, so for any $z>0$ we have $p_{\gamma +1} (z)\ne 0$. This argument is in accordance with the restriction for $p_{\gamma +1}(z)$. We can therefore consider three cases: $p_{\gamma +1}(z)=z^4$, and $p_{\gamma +1}(z)=z^4\pm 6 z^3+10z^2$. The latter two cases are taken as a generalization of the first one.

Figure 1 shows $\rho ^e(r)$ obtained from the numerical integration of Eq. (23) with the Krasnikov form factor and $n=1, 5, 10$. The left panel is for $M=10$, the right panel for $M=1$. Since $\rho ^e(r) \propto M$, if we change $M$ we change the scale, without altering the shape of $\rho ^e(r)$. For $n\ge 2$, $\rho ^e$ is not monotonic and can assume negative values. Because of that, it is possible to have more than two horizons. These plots show also that the effective energy density $\rho ^e$ approaches a finite value for $r\rightarrow 0$. Figure 2 shows the corresponding $F(r)$ functions. For $M=10$, we find at least two horizons, while for $M=1$ there is no horizon. For a large $n$, the oscillations of $\rho ^e$ are stronger and therefore it is possible to form more than two horizons. However, this multi-horizon situation only exists when $M\sim 10$ and $n$ is large. For instance, we found that there are just two horizons when $M=100$ and $n=10$.

Fig. 1

Effective energy density as a function of the radial coordinate for the Krasnikov form factor. Left panel $\rho ^e(r)$ for $M=10$ and $n=1$ (solid line), 5 (dotted line), and 10 (dashed line). Right panel as in the left panel for $M=1$. The two plots have exactly the same shape and only differ in the scale of the vertical axis

Fig. 2

$F$ as a function of the radial coordinate for the Krasnikov form factor. Left panel $F(r)$ for $M=10$ and $n=1$ (solid line), 5 (dotted line), and 10 (dashed line). The three curves cross at least two times the $F=0$ axis and therefore every black hole has at least two horizons. Right panel as in the left panel for $M=1$. These configurations have no horizon as a consequence of the small mass

Figures 3 and 4 are for the Tomboulis form factor. Figure 3 shows the effective energy density $\rho ^e(r)$: like for the Krasnikov form factor, $\rho ^e$ is finite for $r=0$ and it has an oscillatory behavior near $\rho ^e = 0$, so that it can be negative at some radii. Figure 4 shows the function $F(r)$. For $M=10$ we have two horizons, while there is no horizon when $M=1$. The choice of $p_{\gamma +1}(z)$ mainly affects the region $r < 2M$.

Fig. 3

Effective energy density as a function of the radial coordinate for the Tomboulis form factor. Left panel $\rho ^e(r)$ for $M=10$ and $p_{\gamma +1}(z)=z^4$ (solid line) and $z^4+6z^3+10z^2$ (dashed line). Right panel $\rho ^e(r)$ for $M=10$ and $p_{\gamma +1}(z)=z^4$ (solid line) and $z^4-6z^3+10z^2$ (dashed line)

Fig. 4

$F$ as a function of the radial coordinate for the Tomboulis form factor. Left panel $F(r)$ for $M=10$ and $p_{\gamma +1}(z)=z^4$ (solid line), $z^4+6z^3+10z^2$ (dotted line), and $z^4-6z^3+10z^2$ (dashed line). The three curves cross two times the $F=0$ axis and therefore every black hole has two horizons. Right panel as in the left panel for $M=1$. These configurations have no horizon as a consequence of the small mass

4 Nonlocal gravity inspired collapse

Now we want to find the quantum-gravity corrected solution of the gravitational collapse for a homogeneous and spherically symmetric cloud. The scale factor $a(t)$ is determined through the propagator approach. We first write the metric as a flat Minkowski background plus a fluctuation $h_{\mu \nu }$,

$$\begin{aligned} g_{\mu \nu }&= \eta _{\mu \nu } + \kappa \, h_{\mu \nu }, \nonumber \\ \mathrm{d}s^2&= - \mathrm{d}t^2 + a(t)^2 \mathrm{d}x^i \mathrm{d}x^j \delta _{i j}, \end{aligned}$$

(31)

where $\eta _{\mu \nu } = \mathrm{diag}(-1,1,1,1)$. The conformal scale factor $a(t)$ and the fluctuation $h_{\mu \nu }(t, \vec {x})$ are related:

$$\begin{aligned} a^2(t)&= 1 - \kappa h(t), \nonumber \\ h(t=-t_0)&= 0, \nonumber \\ g_{\mu \nu }(t=-t_0)&= \eta _{\mu \nu }, \nonumber \\ h_{\mu \nu }(t, \vec {x} )&= - h(t) \, \mathrm{diag}(0, \delta _{i j} ) \equiv - h(t) \, \mathcal {I}_{\mu \nu }. \end{aligned}$$

(32)

After a gauge transformation, we can rewrite the fluctuation in the usual harmonic gauge,

$$\begin{aligned}&h_{\mu \nu }(x) \rightarrow h^{\prime }_{\mu \nu }(x) = h_{\mu \nu }(x)+ \partial _{\mu } \xi _{\nu } + \partial _{\nu } \xi _{\mu } , \nonumber \\&\xi _{\mu }(t) = \frac{3 \kappa }{2} \, \left( \int _0^{t} h(t') \mathrm{d}t',0,0,0 \right) . \end{aligned}$$

(33)

The fluctuation now reads

$$\begin{aligned}&h^{\prime }_{\mu \nu }(t, \vec {x} ) = h(t) \, \mathrm{diag} ( 3, - \delta _{i j} ), \nonumber \\&h^{\prime \, \mu }_{\mu }(t, \vec {x} ) = - 6 h(t). \end{aligned}$$

(34)

We can then switch to the standard gravitational “barred” field $\bar{h}^{\prime }_{\mu \nu }$ defined by

$$\begin{aligned} \bar{h}^{\prime }_{\mu \nu } = {h}^{\prime }_{\mu \nu } - \frac{1}{2} \eta _{\mu \nu } \, h^{\prime \, \lambda }_{\lambda } = 2 h(t) \, \mathcal {I}_{\mu \nu }, \end{aligned}$$

(35)

satisfying $\partial ^{\mu } \bar{h}^{\prime }_{\mu \nu } = 0$. The Fourier transform of $\bar{h}^{\prime }_{\mu \nu }$ is

$$\begin{aligned} \tilde{\bar{h}}^{\prime }_{\mu \nu }(E, \vec {p}) = 2 \tilde{h}(E) (2 \pi )^3 \delta ^3(\vec {p}) \, \mathcal {I}_{\mu \nu }. \end{aligned}$$

(36)

The classical solution for the homogeneous and spherically symmetric gravitational collapse is known. We can thus compute the Fourier transform $\tilde{h}(E)$ defined in (36). For $\omega \ne -1$, we have

$$\begin{aligned} \tilde{h}(E)=\frac{2\pi \delta (E)}{\kappa } +\frac{2\Gamma \left( \frac{4}{3(\omega +1)}+1\right) \mathrm{sin} \left( \frac{\pi }{2}\frac{4}{3(\omega +1)}\right) }{\kappa t_0^{\frac{4}{3(\omega +1)}} \left| E \right| ^{\frac{4}{3(\omega +1)}+1}}. \end{aligned}$$

(37)

In the case of radiation and dust, we have

$$\begin{aligned} \tilde{h}(E)&= \frac{2\pi \delta (E)}{\kappa } +\frac{2}{\kappa t_0 E^2}, \quad \text {(radiation)}, \end{aligned}$$

(38)

$$\begin{aligned} \tilde{h}(E)&= \frac{2\pi \delta (E)}{\kappa }+ \frac{4\Gamma \left( \frac{4}{3}\right) }{\sqrt{3} \kappa t_0^{4/3} | E | ^{7/3}}, \quad \text {(dust)} . \end{aligned}$$

(39)

The gauge independent part of the graviton propagator for the theory (17) and energy-momentum tensor $\tilde{T}^{\rho \sigma }(p)$ is [21]

$$\begin{aligned}&\mathcal {O}^{-1}_{\mu \nu \rho \sigma }(p) = \frac{V(p^2/\Lambda ^2) }{ p^2} \left( P^{(2)}_{\mu \nu \rho \sigma } - \frac{1}{2} P^{(0)}_{\mu \nu \rho \sigma } \right) \nonumber \\&\Longrightarrow \, \bar{h}^{\prime }_{\mu \nu }(x) = \kappa \! \int \! \frac{\mathrm{d}^4 p}{(2 \pi )^4} \mathcal {O}^{-1}_{\mu \nu \rho \sigma }(p) \tilde{T}^{\rho \sigma }(p) \, \mathrm{e}^{i p x}, \end{aligned}$$

(40)

where $P^{(2)}_{\mu \nu \rho \sigma }$ and $P^{(0)}_{\mu \nu \rho \sigma }$ are the graviton projectors,

$$\begin{aligned}&P^{(2)}_{\mu \nu \rho \sigma } = \frac{1}{2} (\theta _{\mu \rho }\theta _{\nu \sigma } + \theta _{\mu \sigma }\theta _{\nu \rho }) - \frac{1}{3} \theta _{\mu \nu }\theta _{\rho \sigma }, \nonumber \\&P^{(0)}_{\mu \nu \rho \sigma } = \frac{1}{3} \theta _{\mu \nu }\theta _{\rho \sigma } \end{aligned}$$

(41)

and $\theta _{\mu \nu } = \eta _{\mu \nu } - k_\mu k_\nu /k^2$. Therefore

$$\begin{aligned} h(t)&= \kappa \int \frac{\mathrm{d}^4 p}{(2 \pi )^4} V \left( \frac{ - p^2}{\Lambda ^2}\right) \, \tilde{h}(E, \vec {p} ) \, \mathrm{e}^{ i p x} \nonumber \\&= \kappa \int \frac{\mathrm{d} E}{2 \pi } V \left( \frac{E^2}{\Lambda ^2}\right) \, \tilde{h}(E) \mathrm{e}^{- i E t}, \end{aligned}$$

(42)

where

$$\begin{aligned} \tilde{h}(E, \vec {p} ) = (2 \pi )^3 \delta ^3(\vec {p}) \tilde{h}(E). \end{aligned}$$

(43)

If we know the classical solution $a(t)$, we can find the distribution $\tilde{h}(E)$ that provides the correct solution for $V(-p^2/\Lambda ^2) =1$. We can then use a different form factor to find the corresponding quantum-gravity corrected scale factor $a(t)$. Here we want to find the solutions for the gravitational collapse of a cloud of dust and radiation with the form factors of Krasnikov and Tomboulis.

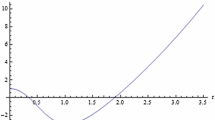
Figure 5 shows the scale factor $a(t)$ (left panel) and the energy density (right panel) for the Krasnikov form factor with $n=2$ and 6 in the case of a cloud of radiation, $\omega = 1/3$. The dust case is shown in Fig. 6. Classically, the scale factor $a(t)$ monotonically decreases and finally vanishes. The corresponding energy density $\rho (t)$ therefore diverges at the time $t=0$. In the quantum-gravity corrected picture, we find a bounce: $a(t)$ reaches a minimum and then start increasing. Far from the bounce, the classical and the quantum solutions are similar, while the difference becomes important at high densities.

Fig. 5

Scale factor $a(t)$ (left panel) and energy density $\rho (t)$ (right panel) for the gravitational collapse of a homogeneous and spherically symmetric cloud of radiation in the Krasnikov model. The solid line is for the classical solution and the singularity occurs at the time $t=0$ when $a=0$. The dotted line is for the Krasnikov model with $n=2$, while the dashed line is for the one with $n=6$

Fig. 6

As in Fig. 5 for the dust case

The calculations with the Tomboulis form factor turn out to be significantly more complicated. We thus use the following approximated form factor:

$$\begin{aligned} V(z)\approx {\left\{ \begin{array}{ll} \mathrm{e}^{-\frac{1}{2}p_{\gamma +1}(z)^2} \approx 1-\frac{1}{2}p_{\gamma +1}(z)^2 &{}\quad \text {if } | p_{\gamma +1}(z) | \le 1, \\ \mathrm{e}^{-\frac{\gamma _E}{2}}\frac{1}{| p_{\gamma +1}(z) | } &{} \quad \text {if } | p_{\gamma +1}(z) | > 1. \end{array}\right. } \end{aligned}$$

(44)

As shown in Fig. 7, such an approximated form factor is very similar to the exact one, with a tiny deviation near $z=\pm 1$. While such an approximated form factor has a discontinuity at $z=\pm 1$, the Fourier transform is applicable as the limits at $z=\pm 1$ in both directions are well defined. Here we have only studied the minimal renormalizable theory with $\gamma =3$ and have chosen $p_{\gamma +1}(z)=z^4$. The part $| p_{\gamma +1}(z) |> 1$ is trivial and we can obtain an analytic result. For the other part of the integral, we need to use a regularization prescription and separate the finite and the divergent parts. The detailed calculation is in Appendix B. Figures 8 and 9 show, respectively, the radiation and the dust case. The qualitative behavior of the scale factor $a(t)$ and the energy density $\rho (t)$ is the same as the one of the Krasnikov model.

Fig. 7

Exact (solid line) and approximated (dashed line) Tomboulis form factor

Fig. 8

Scale factor $a(t)$ (left panel) and energy density $\rho (t)$ (right panel) for the gravitational collapse of a homogeneous and spherically symmetric cloud of radiation in the Tomboulis model. The solid line is for the classical solution and the singularity occurs at the time $t=0$ when $a=0$. The dotted line is for the Tomboulis model with $p_{\gamma +1}(z)=z^4$

Fig. 9

As in Fig. 8 for the dust case

5 Summary and conclusions

In the present paper, we have studied both the static black hole solution and the homogeneous spherically symmetric collapse of a cloud of matter in a super-renormalizable and asymptotically free theory of gravity. The spacetime singularity predicted in classical general relativity is removed in both cases. In the literature there were so far some scattered results in different theoretical frameworks. Here we have studied this issue in more detail within the Krasnikov and Tomboulis models.

Static and spherically symmetric singularity-free black hole solutions have been obtained. At the origin, the effective energy density is always finite and positive, independently of the exact expression of the form factor $V(z)$. In other words, these black holes have a de Sitter core in their interior, where the effective cosmological constant is of order $\kappa ^2 M \Lambda$, $\kappa ^2 = 32\pi G_\mathrm{N}$, $M$ is the black hole mass, and $\Lambda$ is the energy scale of the theory which is naturally to expect to be close to the Planck mass. The singularity of the spacetime is therefore avoided due to the repulsive behavior of the gravitational force. For a large family of form factors, the effective energy density can be negative in some regions, which eventually provides the possibility of having multi-horizon black holes. In the homogeneous and spherically symmetric collapse of a cloud of matter, the formation of the singularity is always replaced by a bounce. Far from the bounce, the collapse follows the classical solution, while it departs from it at high densities. Strictly speaking, asymptotic freedom is sufficient to remove the singularity, but the presence of a bounce requires also a repulsive character for gravitational field in the high energy regime.

In conclusion, we have provided some convincing examples that show how the final products of the quantum-gravity corrected collapse solutions are not the quantum-gravity corrected Schwarzschild black hole metrics. This is not the result that one would expect a priori. There may be three natural explanations.

• 1. Static regular black holes cannot be created in any physical process. In this case, even if they are solution of a theory, they are much less interesting than their classical counterparts that can be created in a collapse.

• 2. The final product of the gravitational collapse is not unique. The collapse of a homogeneous and spherically symmetric cloud of matter does not produce a static regular black hole, but the collapsing matter bounces and then expands. With different initial conditions, not known at the moment, static regular black holes may form.

• 3. The simple example of a homogeneous cloud of matter oversimplifies the picture and misses important physics. As discussed in Sect. 2, in the classical dust case we have a homogeneous interior and a Schwarzschild exterior without ingoing or outgoing flux through any spherical shell of comoving radial coordinate $r$. However, that is not true in general, and the exterior spacetime is a generalized Vaidya solutions with ingoing or outgoing flux of energy. This means that the homogeneous solution is not stable and must evolve to an inhomogeneous model. While the bounce can still occur, after it the collapsing matter may not expand forever. The boundary effects are important and, after proper readjustment that can unlikely be described without a numerical strategy, the collapse approaches the static black hole solution.

The possibility 1 excludes the possibilities 2 and 3, but the latter may also coexist. Here we have focused on the asymptotically free gravity theory with the Lagrangian given in Eq. (17), and we have shown that the issue indeed exists. The theoretical model is not sick, and therefore we cannot attribute the problem to the fact that we are considering a non-consistent quantum theory. However, it is easy to compute the propagator for this class of theories around de Sitter spacetime background and to show the presence of a ghost when the cosmological constant exceeds the square of the Planck mass (this work is in preparation). This fact may explain the fact that our static black holes are not the final product of the gravitational collapse. These black holes have indeed a de Sitter core in which the effective cosmological constant is $\kappa ^2 M \Lambda$. If the black hole mass $M$ exceeds the Planck mass, there is a ghost and the black hole is unstable. Therefore the solutions here presented cannot be the final product, but only an intermediate phase of the gravitational collapse.

Appendices

Appendix A: Theoretical framework

For the theories studied in this paper, the classical action is

$$\begin{aligned} \mathcal {S} = \int \mathrm{d}^4 x \frac{2 \sqrt{|g|}}{\kappa ^2} \left[ R - G_{\mu \nu } \frac{ V(-\Box /\Lambda ^2)^{-1} -1}{\Box } R^{\mu \nu } \right] ,\nonumber \\ \end{aligned}$$

(A1)

where $G_{\mu \nu }$ is the Einstein tensor and $\kappa ^2 = 32 \pi G_\mathrm{N}$. All the non-polynomiality is in the form factor $V(-\Box /\Lambda ^2)$, which must be an entire function. $\Lambda$ is the Lorentz invariant energy scale and it is not subject to infinite or finite (non analytic) renormalizations. The natural value of $\Lambda$ is of order the Planck mass and in this case all the observational constraints are satisfied. Indeed, at classical level all the corrections to the Einstein–Hilbert action are suppressed by $1/\Lambda$, and if the value of $\Lambda$ is large the theory can reduce to general relativity at low energies. At quantum level, the introduction of nonlocal operators in the action could potentially lead to strong nonlocalities generated by the renormalization group flow toward the infrared, in disagreement with observations. This is not the case here, as a consequence of the Donoghue argument [22] and of the fact that our action only involves entire functions.

The entire function $V(-\Box /\Lambda ^2)$ must have no poles in the whole complex plane, in order to ensure unitarity, and must exhibit at least logarithmic behavior in the ultraviolet regime, to give super-renormalizablitity at the quantum level. The theory is uniquely specified once the form factor is fixed, because the latter does not receive any renormalization: the ultraviolet theory is dominated by the bare action (that is, counterterms are negligible). In this class of theories, we only have the graviton pole. Since $V(z)$ is an entire function, there are no ghosts and no tachyons, independently of the number of time derivatives present in the action. This is the main reason to introduce a non-polynomial Lagrangian. At the phenomenological level the form factor could be experimentally constrained, for example measuring the corrections to the gravitational potential, or hypothetically measuring a cross section in a scattering process at high energy. Concerning the difficulties with particular form factors and nonlocal operators, we note that the class of operators introduced by Krasnikov and by Tomboulis are well defined in the Euclidean as well as in the Lorentzian case, because $(k_\mathrm{E}^2)^2 = (k^2)^2$, where $k_\mathrm{E}$ is the momentum in the Euclidean space [19].

More details on the ultraviolet and infrared properties of this class of theories can be found in [17]. We note that here it is possible to anti-screen gravity in the UV without introducing extra degrees of freedom because the theory is characterized by an entire function that goes to zero in the UV. We present two different ways to see this below.

Tree-level unitarity The general and clear way to address the unitarity problem in Lagrangian formalism can be summarized as follows (for more details, see [23–27]): (1) we calculate the propagator expanding the action to the second order in the graviton fluctuation, (2) we calculate the amplitude with general external energy tensor sources, and (3) we evaluate the residue at the poles. A general theory is well defined if “tachyons” and “ghosts” are absent, in which case the corresponding propagator has only first poles at $k^2 - M^2 =0$ with real masses (no tachyons) and with positive residues (no ghosts). In our class of theories, we only have one pole in $k^2 = 0$ with positive residue.

When we introduce a general source, the linearized action including the gauge-fixing reads

$$\begin{aligned} \mathcal {L}_{hT} = \frac{1}{2} h^{\mu \nu } \mathcal {O}_{\mu \nu \rho \sigma } h^{\rho \sigma } - g \, h_{\mu \nu } T^{\mu \nu }, \end{aligned}$$

(A2)

where

$$\begin{aligned} \mathcal {O}^{-1}_{\mu \nu \rho \sigma }(p) = \frac{V(p^2/\Lambda ^2) }{ p^2} \left( P^{(2)}_{\mu \nu \rho \sigma } - \frac{1}{2} P^{(0)}_{\mu \nu \rho \sigma } \right) , \end{aligned}$$

(A3)

$P^{(2)}_{\mu \nu \rho \sigma }$ and $P^{(0)}_{\mu \nu \rho \sigma }$ are the graviton projectors

$$\begin{aligned}&P^{(2)}_{\mu \nu \rho \sigma } = \frac{1}{2} (\theta _{\mu \rho }\theta _{\nu \sigma } + \theta _{\mu \sigma }\theta _{\nu \rho }) - \frac{1}{3} \theta _{\mu \nu }\theta _{\rho \sigma } \nonumber \\&P^{(0)}_{\mu \nu \rho \sigma } = \frac{1}{3} \theta _{\mu \nu }\theta _{\rho \sigma }, \end{aligned}$$

(A4)

and $\theta _{\mu \nu } = \eta _{\mu \nu } - k_\mu k_\nu /k^2$. The transition amplitude in momentum space is

$$\begin{aligned} \mathcal {A} = g^2 \, T^{\mu \nu } \, \mathcal {O}^{-1}_{\mu \nu \rho \sigma } \, T^{\mu \nu }, \end{aligned}$$

(A5)

where $g$ is an effective coupling constant. To make the analysis more explicit, we can expand the sources using the following set of independent vectors in the momentum space:

$$\begin{aligned} k^{\mu }&= (k^0, \vec {k}), \,\, \tilde{k}^{\mu } = (k^0, - \vec {k}), \,\, \epsilon ^{\mu }_i = (0, \vec {\epsilon }), \nonumber \\&i =1, \dots , D-2, \end{aligned}$$

(A6)

where $\vec {\epsilon }_i$ are unit vectors orthogonal to each other and to $\vec {k}$. The symmetric stress-energy tensor reads

$$\begin{aligned} T^{\mu \nu }&= a k^{\mu } k^{\nu } + b \tilde{k}^{\mu } \tilde{k}^{\nu } + c^{i j} \epsilon _i^{(\mu } \epsilon _j^{\nu )}\nonumber \\&+\,\, d \, k^{(\mu } \tilde{k}^{\nu )} + e^i k^{(\mu } \epsilon _i^{\nu )} + f^i \tilde{k}^{(\mu } \epsilon _i^{\nu )}. \end{aligned}$$

(A7)

The conditions $k_{\mu } T^{\mu \nu } =0$ and $k_{\mu } k_{\nu }T^{\mu \nu } =0$ place constrains on the coefficients $a,b,d, e^i, f^i$. Introducing the spin projectors and the conservation of the stress-energy tensor $k_{\mu } T^{\mu \nu } = 0$ in (A5), the amplitude results

$$\begin{aligned} \mathcal {A} = g^2 \left\{ T_{\mu \nu } T^{\mu \nu } - \frac{T^2}{D-2} \right\} \frac{\mathrm{e}^{- H(k^2/\Lambda ^2)}}{k^2}, \end{aligned}$$

(A8)

where $T = T^\mu _\mu$. Clearly, there is only the graviton pole in $k^2 =0$ and the residue at $k^2=0$ is

$$\begin{aligned} \mathrm{Res} \, ( \mathcal {A} ) \big |_{k^2 =0} = g^2 \left[ (c^{ij})^2 - \frac{ (c^{ii})^2}{D-2} \right] \Big |_{k^2 =0}. \end{aligned}$$

(A9)

For $D>3$, we find that $\mathrm{Res} \, ( \mathcal {A} ) \big |_{k^2 =0}>0$ (because $H(0) =0$), which means that the theory is unitary. Instead, for $D=3$ the graviton is not a dynamical degree of freedom and the amplitude is zero.

As an example of this quantum transition, we can consider the interaction of two static point particles. Here $T^{\mu }_{ \nu } = \mathrm{diag}(\rho ,0,0,0)$ with $\rho = M \, \delta (\vec {x})$ and the amplitude (A8) simplifies to

$$\begin{aligned} \mathcal {A} = g^2 \, M^2 \left( \frac{D-3}{D-2} \right) \, \frac{\mathrm{e}^{- H(k^2/\Lambda ^2)}}{k^2}, \end{aligned}$$

(A10)

which is positive in $D>3$ and zero for $D=3$ since, again, there are no local degrees of freedom in $D=3$.

Källén–Lehmann (KL) representation Any action in the class of theories here presented is defined in terms of an entire function with no zeros, singularities, nether poles. Therefore the usual derivation of the KL decomposition goes straightforward. Let us construct step by step such representation for a weakly nonlocal prototype theory. It is easy to show that

$$\begin{aligned} \int \frac{\mathrm{d}^3 \vec {p} }{(2 \pi )^3 2 E_{\vec {p}}} = \int \frac{\mathrm{d}^4 p }{(2 \pi )^4 } \delta (p^2 - m_{\lambda }^2) \theta (p^0) \mathrm{e}^{- H(p^2 - m_{\lambda }^2 )}.\nonumber \\ \end{aligned}$$

(A11)

Therefore a complete set of states satisfy

$$\begin{aligned} \mathbf{1} = | 0 \rangle \langle 0 | + \sum _{\lambda } \int \frac{\mathrm{d}^3 \vec {p} }{(2 \pi )^3 2 E_{\vec {p}}} | \lambda _{\vec {p}} \rangle \langle \lambda _{\vec {p}} | \end{aligned}$$

(A12)

where we defined the state $\lambda _{\vec {p}}$ by boosting of an arbitrary boost $\vec {p}$ a momentum zero state $\lambda _0$ and we summed over all $\vec {p}$. Assuming $\langle 0 | \phi (x) | 0 \rangle =0$ and Lorentz invariance of $\phi (0)$,

$$\begin{aligned} \langle 0 | \phi (x) | \lambda _{\vec {p}} \rangle = \mathrm{e}^{- i p x} \langle 0 | \phi (0) | \lambda _{\vec {p}} \rangle = \mathrm{e}^{- i p x} \langle 0 | \phi (0) | \lambda _{0} \rangle \Big |_{p_0 = E_{\vec {p}} }\, .\nonumber \\ \end{aligned}$$

(A13)

We thus get for $x_0 > y_0$

$$\begin{aligned}&\langle 0 | \phi (x) \phi (y) | 0 \rangle \Big |_{x_0 > y_0} = \sum _{\lambda } \int \frac{\mathrm{d}^3 \vec {p} }{(2 \pi )^3 2 E_{\vec {p}}} \mathrm{e}^{- i p (x-y)} \Big |_{p_0 = E_{\vec {p}} }\nonumber \\&| \langle 0 | \phi (0) | \lambda _{0} \rangle |^2 \nonumber \\&\qquad = \sum _{\lambda } \int _{C_F} \frac{\mathrm{d}^4 p }{(2 \pi )^4 } \frac{i }{(p^2 - m_{\lambda }^2) \, \mathrm{e}^{H(p^2 - m_{\lambda }^2)} } \, \mathrm{e}^{- i p (x-y)} \nonumber \\&| \langle 0 | \phi (0) | \lambda _{0} \rangle |^2 \nonumber \\&\qquad = \sum _{\lambda } \mathrm{e}^{- H(- \Box - m_{\lambda }^2)} \int _{C_F} \frac{\mathrm{d}^4 p }{(2 \pi )^4 } \frac{i }{(p^2 - m_{\lambda }^2) \, } \, \mathrm{e}^{- i p (x-y)} \nonumber \\&| \langle 0 | \phi (0) | \lambda _{0} \rangle |^2 \nonumber \\&\qquad \rightarrow \sum _{\lambda } \mathrm{e}^{- H(- \Box - m_{\lambda }^2)} \int _{ R } \frac{\mathrm{d}^4 p }{(2 \pi )^4 } \frac{i }{(p^2 - m_{\lambda }^2 + i \epsilon ) \, } \, \mathrm{e}^{- i p (x-y)} \nonumber \\&| \langle 0 | \phi (0) | \lambda _{0} \rangle |^2 \nonumber \\&\qquad = \sum _{\lambda } \int _{ R } \frac{\mathrm{d}^4 p }{(2 \pi )^4 } \frac{i \, \mathrm{e}^{- H(p^2 - m_{\lambda }^2)} }{(p^2 - m_{\lambda }^2 + i \epsilon ) \, } \, \mathrm{e}^{- i p (x-y)} \nonumber \\&| \langle 0 | \phi (0) | \lambda _{0} \rangle |^2, \end{aligned}$$

(A14)

where the contour $C_F$ is closed in the lower half $p_0$-plane, while the integral along the real axes is evaluated displacing the poles for $\mathrm{Re}(p_0) > 0$ in the lower half plane and for $\mathrm{Re}(p_0) < 0$ in the upper half plane (in our gravitational theory $m_{\lambda } = 0$). An analog relation is obtained for $x_0<y_0$, therefore:

$$\begin{aligned}&\langle 0 | \mathrm{T} ( \phi (x) \phi (y) ) | 0 \rangle = \sum _{\lambda } \int _{ R } \frac{\mathrm{d}^4 p }{(2 \pi )^4 } \frac{i \, \mathrm{e}^{- H(p^2 - m_{\lambda }^2)} }{(p^2 - m_{\lambda }^2 + i \epsilon ) \, }\nonumber \\&\quad \times \, \mathrm{e}^{- i p (x-y)}| \langle 0 | \phi (0) | \lambda _{0} \rangle |^2. \end{aligned}$$

(A15)

The matrix element is Lorentz invariant and only depends on the mass of the state $m_{\lambda }$, therefore we can write (A15) making use of the definite positive spectral density function $\rho (s)$ defined by

$$\begin{aligned} \rho (s) = \sum _{\lambda } \delta (s - m_{\lambda }^2) \, | \langle 0 | \phi (0) | \lambda _{0} \rangle |^2, \end{aligned}$$

(A16)

as follows:

$$\begin{aligned} \langle 0 | \mathrm{T} ( \phi (x) \phi (y) ) | 0 \rangle = \int _0^{+ \infty } \!\!\! \mathrm{d}s \, \Delta _F(x-y;s) \rho (s), \end{aligned}$$

(A17)

where we defined the function

$$\begin{aligned} \Delta _F(x-y; m_{\lambda }^2) = \int _{ R } \frac{\mathrm{d}^4 p }{(2 \pi )^4 } \frac{i \, \mathrm{e}^{- H(p^2 - m_{\lambda }^2)} }{(p^2 - m_{\lambda }^2 + i \epsilon ) \, } \, \mathrm{e}^{- i p (x-y)},\nonumber \\ \end{aligned}$$

(A18)

in analogy with the Feynman propagator. The spectral representation sees all the poles, but in this case they are the same as in general relativity, because we have introduced a function with no poles or zeros. In the case of a local theory with a finite number of derivatives, this is impossible and the theory is sick.

We expect a single particle state to contribute to $\rho (s)$ as an isolated delta

$$\begin{aligned}&\langle 0 | \mathrm{T} ( \phi (x) \phi (y) ) | 0 \rangle = \int _0^{+ \infty } \!\!\! \mathrm{d}s \int _{ R } \frac{\mathrm{d}^4 p }{(2 \pi )^4 }\nonumber \\&\quad \times \frac{i \, \mathrm{e}^{- H(p^2 - m_{\lambda }^2)} }{(p^2 - m_{\lambda }^2 + i \epsilon ) \, } \, \mathrm{e}^{- i p (x-y)}\nonumber \\&\quad \times \delta (s - m_{\lambda }^2) \, Z \quad \quad ( Z>0). \end{aligned}$$

(A19)

Appendix B: Integrals with the Tomboulis form factor

We use the approximated form factor in Eq. (44). Let us first consider the radiation case. For $| p_{\gamma +1}(z) | \ge 1$, the integral is trivial. When $| p_{\gamma +1}(z) | \le 1$, we have

$$\begin{aligned} \int _{-1}^{1} \frac{\mathrm{d}E}{2\pi } \left( 1-\frac{ p_{\gamma +1}(z)^2}{2}\right) \frac{2}{t_0 E^2} \mathrm{e}^{iEt}. \end{aligned}$$

(B1)

The second term with $p_{\gamma +1}(z)^2$ is trivial, in the sense that it has an analytic result. We thus want to find the solution of the first term which, apart a constant coefficient, has the form

$$\begin{aligned} I\equiv \int _{-1}^{1} \mathrm{d}E \frac{\mathrm{e}^{\mathrm{i}Et}}{E^n}, \end{aligned}$$

(B2)

where $n$ is an even integer, so that the integral gives a real result and is an even function of $t$. In the case of radiation, $n=2$.

This integral can be calculated with the residue theorem. We introduce a small number $\mu$, so that the pole of order $n$ at $E=0$ is reduced to $n$ simple poles. To include all the poles, we can consider contour integrals of both the upper and the lower circles. Writing $E=\rho \mathrm{e}^{\mathrm{i}\theta }$, $\mathrm{d}E=iE\mathrm{d}\theta$, and we have

$$\begin{aligned}&I\!+\!\int _{\begin{array}{c} \theta =0 \\ \rho =1 \end{array}}^{\theta =\pi } \mathrm{d}E \frac{\mathrm{e}^{\mathrm{i}Et}}{E^n} \equiv I\!+\!I_1 \!=\!2\pi i \sum _{\begin{array}{c} \mu _i \text {in upper} \\ \text {unit circle} \end{array} }\mathrm{Res} \left( \frac{\mathrm{e}^{\mathrm{i}Et}}{E^n+\mu ^n} \right) \nonumber \\&\quad +\pi i\sum _{\begin{array}{c} \mu _i \text {on} \\ \text {real axis} \end{array} } \mathrm{Res} \left( \frac{\mathrm{e}^{\mathrm{i}Et}}{E^n+\mu ^n} \right) \end{aligned}$$

(B3)

and

$$\begin{aligned}&I+\int _{\begin{array}{c} \theta =0 \\ \rho =1 \end{array}}^{\theta =-\pi } \mathrm{d}E \frac{\mathrm{e}^{\mathrm{i}Et}}{E^n} \equiv I+I_2\nonumber \\&\quad =2\pi i \sum _{\begin{array}{c} \mu _i \text {in the lower} \\ \text {unit circle} \end{array} } \mathrm{Res} \left( \frac{\mathrm{e}^{\mathrm{i}Et}}{E^n\!+\!\mu ^n} \right) \nonumber \\&\qquad -\pi i\sum _{\begin{array}{c} \mu _i \text {on the} \\ \text {real axis} \end{array} } \mathrm{Res} \left( \frac{\mathrm{e}^{\mathrm{i}Et}}{E^n\!+\!\mu ^n} \right) .\nonumber \\ \end{aligned}$$

(B4)

The combination of the two equations gives the result of $I$

$$\begin{aligned} I=-\frac{1}{2} (I_1+I_2)+D, \end{aligned}$$

(B5)

where

$$\begin{aligned} I_1+I_2&= \int _{\theta =0}^{\pi } \mathrm{d} \theta \{ \mathrm{e}^{-t\sin \theta } \sin [(n-1)\theta -t\cos \theta ]\nonumber \\&+\,\,\mathrm{e}^{t\sin \theta } \sin [(n-1)\theta +t \cos \theta ]\}, \end{aligned}$$

(B6)

and the divergence $D$ of order $\mu ^{n-1}$ is given by

$$\begin{aligned} D=\pi i\left( \sum _{\begin{array}{c} \mu _i \text {in the upper} \\ \text {unit circle} \end{array} } -\sum _{\begin{array}{c} \mu _i \text {in the lower} \\ \text {unit circle} \end{array} } \right) \mathrm{Res} \left( \frac{e^{\mathrm{i}Et}}{E^n+\mu ^n} \right) .\nonumber \\ \end{aligned}$$

(B7)

For radiation, $n=2$ and we have

$$\begin{aligned} I&= -\frac{1}{2}\int _{\theta =0}^{\pi } \mathrm{d} \theta \{ \mathrm{e}^{-t\sin \theta } \sin [\theta -t\cos \theta ]\nonumber \\&+\,\,e^{t\sin \theta } \sin [\theta +t \cos \theta ]\} +\frac{\pi }{\mu }, \end{aligned}$$

(B8)

where the divergent part is $D=\frac{\pi }{\mu }$ for $\mu \rightarrow 0$.

The dust case is slightly different and it is more convenient to choose the exponential form for approximation of $V(z)$, so the integral is

$$\begin{aligned} I \equiv \int _{-1}^{1} \mathrm{d}E \frac{1}{| E | ^\alpha } \mathrm{e}^{-\frac{E^{16}}{2}} \mathrm{e}^{\mathrm{i}Et} = 2 ~\mathrm{Re} \int _{0}^{1} \mathrm{d}E \frac{1}{ E ^\alpha } \mathrm{e}^{-\frac{E^{16}}{2}} \mathrm{e}^{\mathrm{i}Et},\nonumber \\ \end{aligned}$$

(B9)

where $\alpha >0$ is not an integer. With the transform for the integration variable $E=\rho \mathrm{e}^{i\theta }$, $\mathrm{d}E=\mathrm{i}E\mathrm{d}\theta$, and applying the contour integral we have

$$\begin{aligned}&I_1+I_2+I_R+I_r \equiv \left( \int _{\begin{array}{c} \rho =0 \\ \theta =0 \end{array}}^{\rho =1} + \int _{\begin{array}{c} \rho =1 \\ \theta =2\pi \end{array}}^{\rho =0} +\int _{\begin{array}{c} \theta =0 \\ \rho =1 \end{array}}^{\theta =2\pi } +\int _{\begin{array}{c} \theta =2\pi \\ \rho \rightarrow 0 \end{array}}^{\theta =0} \right) \nonumber \\&\qquad \mathrm{d}E \frac{1}{ E ^\alpha } \mathrm{e}^{-\frac{E^{16}}{2}} \mathrm{e}^{\mathrm {i}Et}=0. \end{aligned}$$

(B10)

The first two terms $I_1+I_2$ can be simplified as

$$\begin{aligned} I_1+I_2=2\int _0^1 \mathrm{d}\rho \frac{1}{\rho ^\alpha } \mathrm{e}^{-\frac{1}{2}\rho ^{16}} \mathrm{e}^{\mathrm{i}\rho t} \mathrm{e}^{-\mathrm{i}\pi \alpha } (i\sin \alpha \pi ). \end{aligned}$$

(B11)

The integration of the unit circle gives the finite part of the required integral, and the integration around the origin gives the divergent part of order $\alpha -1$,

$$\begin{aligned}&I_R =i~\int _0^{2\pi } \mathrm{d}\theta ~\mathrm{e}^{-\frac{1}{2}\cos 16\theta -t\sin \theta } \mathrm{e}^{i [ -\frac{1}{2} \sin 16\theta +t \cos \theta + (1-\alpha ) \theta ]},\nonumber \\ \end{aligned}$$

(B12)

$$\begin{aligned} I_r&= i \int _{2\pi }^{0} \mathrm{d}\theta \nonumber \\&\times \frac{1}{\mu ^{\alpha -1}} \mathrm{e}^{-\frac{\mu ^{16}}{2}\cos 16\theta -\mu t\sin \theta } \mathrm{e}^{i\left[ -\frac{\mu ^{16}}{2} \sin 16\theta + \mu t \cos \theta + (1-\alpha ) \theta \right] } \nonumber \\&\quad \simeq i \int _{2\pi }^{0} \mathrm{d}\theta ~\frac{\mathrm{e}^{i (1-\alpha )\theta }}{\mu ^{\alpha -1}}. \end{aligned}$$

(B13)

Finally, we can get the result

$$\begin{aligned} I&= -\frac{1}{\sin \alpha \pi } \int _0^{2\pi } \mathrm{d}\theta \mathrm{e}^{-\left( \frac{1}{2}\cos 16\theta +t \sin \theta \right) } \nonumber \\&\times \cos \left[ -\frac{1}{2}\cos 16\theta +t \cos \theta +(1-\alpha )\theta +\alpha \pi \right] \nonumber \\&+\frac{2}{(\alpha -1)\mu ^{\alpha -1}}. \end{aligned}$$

(B14)

For the dust case, we have $\alpha =7/3$ and the divergence is of order $4/3$.