Abstract
Interpreting the cosmological constant \(\Lambda \) as a thermodynamic pressure and its conjugate quantity as a thermodynamic volume, we study the Maxwell equal-area law of higher dimensional Gauss–Bonnet–AdS black holes in extended phase space. These black hole solutions critically behave like van der Waals systems. It has been realized that below the critical temperature \(T_\mathrm{c}\) the stable equilibrium is violated. We show through calculations that the critical behaviors for the uncharged black holes only appear in \(d=5\). For the charged case, we analyze solutions in \(d = 5\) and \( d = 6\) separately and find that, up to some constraints, the critical behaviors only appear in the spherical topology. Using the Maxwell construction, we also find the isobar line for which the liquid–gas-like phases coexist.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Recently, the study of thermodynamical properties of the black holes using techniques explored in statistical physics and fluids has received special interest [1–3]. These researches have brought about new understanding of the fundamental physics associated with the critical behaviors of several black holes in various dimensions using either numerical or analytic methods [1, 4–9]. In particular, AdS black holes in arbitrary dimensions have been extensively investigated in many works [9–22]. More precisely, the state equations \(P=P(T,v)\) have been established by considering the cosmological constant as the thermodynamic pressure and its conjugate as the thermodynamic volume. In fact, this issue has opened a new way to study the behavior of the RN-AdS black hole systems using the physics of van der Waals fluids. Indeed, it has been shown that the corresponding \(P\)–\(V\) criticality can be linked to the liquid–gas systems of statistical physics. Moreover, it has been realized that the criticality depends on many parameters including the dimension of the spacetime [10–17, 23, 24].
More recently, a special interest has been devoted to the study of Maxwell’s equal-area law for some black hole solutions. More precisely, the state equations of various AdS black hole in \(P\)–\(v\) diagrams have been worked out showing the existence of undesirable negative pressure. They appear also thermodynamic unstable regions associated with the condition \(\frac{\partial P}{\partial v}>0\). In this way, the corresponding system can be contracted and expanded automatically [18–20, 25–27]. In van der Waals systems, such problems have been overcome by using the Maxwell equal-area approach.
The aim of this work is to contribute to these researches by studying higher dimensional uncharged and charged Gauss–Bonnet–Anti-de Sitter black holes in extended phase space. Considering the cosmological constant \(\Lambda \) as a thermodynamic pressure and its conjugate quantity as a thermodynamic volume, we present the Maxwell equal-area law of higher Gauss–Bonnet–AdS black holes in extended phase space. These black hole solutions involve critical behaviors like the van der Waals gas. We show that below the critical temperature \(T_\mathrm{c}\) the stable equilibrium is violated. Based on the Maxwell construction, we obtain the isobar line for which the liquid–gas phases coexist.
The paper is organized as follows. In Sect. 2, we give an overview on the thermodynamics of higher dimensional Gauss–Bonnet black holes in AdS geometry. In Sect. 3, we first study the equal-area law of Gauss–Bonnet–AdS black hole in extended phase space for uncharged solutions. Next, we extend the analysis to the charged case in five dimensions. Then we present the results for higher dimensions. The last section is devoted to our conclusion.
2 Thermodynamics of Gauss–Bonnet black holes in AdS space
In this section, we give an overview on thermodynamics of Gauss–Bonnet black holes in AdS space. This matter is based on much work by other authors [16, 28–31]. Indeed, we start by considering a \(d\)-dimensional Einstein–Maxwell theory in the presence of the Gauss–Bonnet terms and a cosmological constant \(\Lambda =\,\!-\frac{(d-1)(d-2)}{2l^2}\). The corresponding action reads
where \(\alpha _\mathrm{GB}\) is the Gauss–Bonnet coefficient with dimension \([\mathrm{length}]^2\). In this action, \(F_{\mu \nu }\) is the Maxwell field strength given by \(F_{\mu \nu }=\partial _\mu A_\nu -\partial _\nu A_\mu \) where \(A_\mu \) is an abelian gauge field. Roughly speaking, the discussion will be given here corresponding to the case with a positive Gauss–Bonnet coefficient, namely, \(\alpha _\mathrm{GB}\ge 0\). As shown in [28], dynamical solutions appear only in higher dimensional theories (\(d \ge 5\)). For this reason, it should be interesting to concentrate on such models. In this way, the above action produces a static black hole solution with the following metric:
where \(h_{ij}\mathrm{d}x^i\mathrm{d}x^j\) is the line element of a \((d-2)\)-dimensional maximal symmetric Einstein space with the constant curvature \((d-2)(d-3)k\) and volume \(\Sigma _k\). It is noted that \(k\) takes the three values \(1\), \(0\), and \(-1\), corresponding to the spherical, Ricci flat, and hyperbolic topology of the black hole horizon, respectively. According to [22, 29, 32, 33], the metric function \(f\) takes the following form:

where \(\alpha =(d-3)(d-4)\alpha _\mathrm{GB}\). In this solution, \(M\) represents the black hole mass, \(Q\) is linked to the charge of the black hole, and \(P=\,\!-\frac{\Lambda }{8\pi }\). For a well-defined vacuum solution associated with \(M=Q=0\), the effective Gauss–Bonnet coefficient \(\alpha \) and pressure \(P\) must satisfy the following constraint:
It is recalled that the mass \(M\) can be given in terms of the horizon radius \(r_\mathrm{h}\) of the black hole determined by the largest real root of the equation \(f(r_\mathrm{h})=0\). It takes the following form:
Similarly, the Hawking temperature of the black hole reads

It is worth noting that in the discussion of the thermodynamics of the black hole in the extended phase space by considering the pressure \(P=\,\!-\frac{\Lambda }{8\pi }\), the black hole mass \(M\) should be identified with the enthalpy \(H\equiv M\) rather than the internal energy of the gravitational system [34]. It turns out that many other thermodynamic quantities can be obtained using the thermodynamical equations. For instance, the entropy \(S\), thermodynamic volume \(V\), and electric potential (chemical potential) \(\Phi \) take the following forms:
These thermodynamic quantities satisfy the following differential form:
where
is the conjugate quantity to the Gauss–Bonnet coefficient \( \alpha \), being considered as a variable. By the scaling argument, the generalized Smarr relation for the black holes can be written as
Moreover, many solutions treating other black holes are given in [13, 34]. This class of black hole solutions has volume \(V\sim \Sigma _k r^{d-1}_\mathrm{h}\) and an area given by \(A\sim \Sigma _k r_\mathrm{h}^{d-2}\). In this way, the black hole horizon has a scalar curvature \(R_\mathrm{h} \sim k/r_\mathrm{h}^2\). The Gauss–Bonnet term on the horizon is \(R_\mathrm{GB} \sim k^2/r^4_\mathrm{h}\). In fact, the first term in (11) can be put in the form \(VR_\mathrm{GB}\), while the second term takes the form \( T A R_\mathrm{h}\). It is observed that both terms vanish in the flat solution corresponding to \(k=0\). It is noted that the first term in (11) is nothing but the second term in the black hole mass (5), while the second term in (11) is identified with the second term of the black hole entropy (7) multiplied by Hawking temperature \(T\). Using Legendre transformations, the Gibbs free energy and the Helmholtz free energy read
Moreover, we recall that the Helmholtz free energy \(F\) can be obtained by removing the contribution of the background of the AdS vacuum solution. In this way, only the situation associated with a negative \(F\) can be regarded as the black hole solution considered as a thermodynamically AdS vacuum solution. In the case associated with the hyperbolic horizon (\(k=\,\!-1\)) [35], the black hole entropy (7) could be negative. In fact, a negative entropy has no meaning in statistical physics. For these reasons, the constraints
should be added. It is noted that in the case \(k=\,\!-1\), the metric function \(f\) given in Eq. 3 shows the existence of a minimal horizon radius \(r_\mathrm{h}^2 \ge 2\alpha \). However, the non-negative values of the black hole entropy (7) produce a stronger constraint on the horizon radius given by \(r^2_\mathrm{h} \ge (2+ 4/(d-4))\alpha \).
3 The equal-area law of Gauss–Bonnet–AdS black hole in extended phase space
Having given the essentials on the thermodynamics of the Gauss–Bonnet–Anti-de Sitter black holes, we now move on to investigate the corresponding Maxwell equal-area law.
3.1 The construction of equal-area law in \(P\)–\(v\) diagram
In the study of the van der Waals system for an isotherm below the critical temperature \(T< T_\mathrm{c}\) the two points, of the \((P,v)\) plane, solving the equation
indicate the stability limit of the system. It is observed that the critical point corresponding to the largest volume is interpreted as the stability limit of the gaseous phase. However, the critical point associated with the smallest volume corresponds to the stability limit of the liquid phase. The chemical potential of such thermodynamic systems should satisfy
In the isotherm transformation, the difference of chemical potential between two states with the pressure \(P\) and \(P_0\) should have the following form:
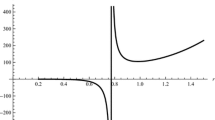
It is realized that the Gauss–Bonnet–AdS black holes present similar behaviors as illustrated in Fig. 1.
It observed from this figure that, at the point \(E\), the black hole lies at “gas” phase. However, at point “A”, the black hole lies at “liquid” phase completely. Moreover, the region between \(A\) and \(E\) can be considered as a coexistence phase. However, the oscillating part of the curve between \(A\) and \(E\) cannot be the coexistence line due to the fact that the part \(BD\) violates the equilibrium conditions. At \(A\) and \(E\), the chemical potentials \(\mu _A (T,P)\) and \( \mu _B (T,P)\) are
This relation produces the thermodynamic condition for the phase equilibrium. Indeed, Eq. (17) gives
showing that the areas \(EDC\) and \(ABC\) are equal.
In what follows, the main aim is to investigate the position of the points \(A\) and \(E\) for Gauss–Bonnet–AdS black holes in higher dimensions. First, we discuss the uncharged case, then we will present numerical solutions for the charged black holes in the next section.
3.2 Uncharged solutions
In this subsection, we discus the neutral case corresponding to \(Q=0\). Identifying the pressure with the cosmological constant and the corresponding conjugate thermodynamic volume, the Hawking temperature (6) can be explored to write down the state equation. The latter reads
To make contact with the van der Waals equation, we should use a series expansion with the inverse of the specific volume \(v\). The calculation leads to
Identifying the specific volume \(v\) with the horizon radius of the black holes as proposed in [9, 13, 21]:
the specific volume \(v\) can be related to the horizon radius \(r_\mathrm{h}\). Using (22), one can recover all the results in terms of \(v\). In this way, Eq. (20) becomes
To obtain the equal-area isobar, \(P=P_0\), one uses the following relations:
and
The equal-area law requires the following equality:
leading to
In the isothermal curves, the points \(v_1\) and \(v_2\) should satisfy
From these equations, one can derive the relations
and
Putting \(x=\frac{v_1}{v_2}\),(\(0\le x\le 1\)), we get the following identities:
and
Using Eqs. (32), (33) and (34), we get a polynomial equation admitting \(v_2^2\) as a real positive root,
where the coefficients \(a\), \(b\), and \(c\) read
Solving the above polynomial equation, we get
In the limit \(x\rightarrow 1\), one should have \(v_1=v_2=v_c\). In what follows, we discuss the convergence of this limit in terms of the topology and the dimension of the spacetime. In fact, three situations can appear. They are classified as follows:
-
In the case of \({ k=0}\), corresponding to flat topology, this limit diverges for any dimensions \(d\). This shows the absence of the critical points. Indeed, this can be seen from the equation of state (23). The latter reduces to \(P=\frac{T}{v}\), indicating that no phase transition can occur.
-
In the case of \({ k=\,\!-1},\) associated with the hyperbolic topology, a negative value of \(v_2^2\) appears in \(d=5\). For \(d\ge 6\), the limit also diverges. This implies that there does not exist any phase transition.
-
In the case of \({ k=1}\), corresponding to the spherical topology, this limit diverges only when \(d\ge 6\). In the case of \(d=5\), we have
$$\begin{aligned} v_c&= \lim _{x\rightarrow 1}\sqrt{\frac{y_1}{y_2}}= 4 \sqrt{\frac{2}{3}\alpha },\quad with \nonumber \\&\quad \left\{ \begin{array}{r c l} y_1&{}= &{} 32 \alpha (x-1)^3 \\ y_2&{}= &{}18 x^2 (x+1) \ln (x)-36 (x-1) x^2. \end{array} \right. \end{aligned}$$(40)
It is noted that a similar result has been found in [28]. Substituting (40) in (33) to eliminate \(v_2\) and setting \(T_0=\chi T_\mathrm{c}\), the critical temperature reads
We can also obtain the following relation:
In Table 1, we present the numerical values of the \(v_{1,2}\) and \(P_0\) for different values of the constant \(\alpha \).
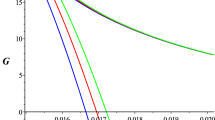
From Table 1, we can see that \(x\) is not linked to the coupling constant \(\alpha \). However, it increases at certain values of \(\chi \). The specific volume \(v_2\) decreases and increases with \(\chi \) and \(\alpha \), respectively. The pressure \(P_0\) increases and decreases with \(\chi \) and \(\alpha \), respectively. For more details, we plot the pressure \(P\) at constant temperature in terms of the specific volume \(v\) for different values of the coupling constant \(\alpha \) (Figs. 2, 3).
For different values of \(\alpha \), we observe that the isobar in the isotherm will be shorter by increasing the temperature. When the temperature reaches the critical one, the boundaries of the isobar coincide, \(v_1=v_2=v_c\).
4 Charged black hole solutions
This section concerns the case of charged Gauss–Bonnet–AdS black holes in the AdS geometry. In this case, the state equation can be written as
A close inspection of this equation shows that one may make a separate study. First, we deal with the five dimensional case. Then we study models associated with \( d \ge 6\).
4.1 Five dimensional case
In \(d=5\), the equation of the state (43) reduces to
Using a similar analysis to the case of uncharged solutions, Eqs. (32), (33), and (34) become, respectively,
and
Using the above equations, we obtain also the polynomial equation of \(v_2\). It is given by
where the coefficients \(a\), \(b\), and \(c\) take now the following form:
The limit \(x\rightarrow 1\), associated with \(v_1=v_2=v_c\), leads to
This shows similarities to the one obtained in [28]. The critical specific volume, which is the positive real root of (53), takes the following form:
with
The corresponding critical temperature reads
As in the uncharged case, we discuss the existence of the critical points for different topologies. In fact, we have three situations:
-
For the flat topology, the apparition of \(k\), in the fourth term in (54), reveals the absence of the critical behavior.
-
For the hyperbolic one, the constraint on the positivity of the temperature and the specific volume does not show critical behavior.
-
For the spherical topology, the existence of the critical point is controlled by the following constraint:
$$\begin{aligned} |Q|\le 6 \alpha . \end{aligned}$$(57)
The Maxwell construction can be obtained using the same analysis as the previous section. This gives rise to an equation depending only on \(x\). To derive the values of \(v_{1,2}\) and \(P_0\), we should find \(x\). For the charged case, we list all these results in Table 2.
It follows from Table 2 that \(P_0\) decreases when one increases \(\alpha \), \(Q\), and \(\chi \). However, the specific volume \(v_2 \) increases when \(\alpha \) and \(\chi \) decrease. In fact, the charge decreases the values of \(v_2\). An important remark that emerges from this calculation is that \(x\) remains constant where we have a proportionality between incremented values of the charge and coupling constant \((\alpha _1,Q_1)\propto (\alpha _2,Q_2)\), showing that the charge and \(\alpha \) can be interrelated [28]. In what follows, we plot the isotherms in the \((P,v)\) diagram and show the equal Maxwell area.
4.2 Higher dimensional cases
The complete form of the equation of states (23) gives also a polynomial equation of \(v_2\). Similar calculations can be done for higher dimensional black holes. In the limit \(x\rightarrow 1\), the specific volume is a real positive solution with the following polynomial form:
The critical temperature reads

It is observed that the Ricci flat topology and the hyperbolic one do not allow for the existence of critical behaviors. Up to some conditions, the critical behaviors appear only in the case of the spherical topology corresponding to \(k=1\). In fact, \(\alpha |Q|^\frac{-2}{(d-3)}\) should not be too large [28]. For reasons of simplicity, we restrict our study to \(d=6\). In particular, we present the numerical results in \(d=6\) for \(x, v_{1,2}\) and \(P_0\) in Table 3.
It is observed from Table 3 that \(P_0\) increases with \(Q\) and \(\chi \). However, the specific volume \(v_2\) decreases with \(Q\) and \(\chi \). The comparison between Tables 2 and 3 shows the effect of the black hole dimensions. In fact, \(P_0\) and \(v_2\) increase and decrease, respectively, with the dimension. To illustrate this effect, we plot these results in Fig. 4, showing the Maxwell equal area.
5 Conclusion
In this paper, we have studied the Maxwell equal-area law of higher dimensional Gauss–Bonnet–anti-de Sitter black holes. The corresponding critical behaviors show similarity to the van der Waals one. We have shown that this construction can be used to eliminate the region of the violated stable equilibrium \(\frac{\partial P}{\partial v} > 0\). In particular, we have found the isobar line in which the two real phases coexist. It has been realized that this construction can be viewed as a simple way to derive the coordinates of the critical points. We have presented numerical calculations showing that the critical behaviors for the uncharged black holes appear only when \(d = 5\). For the charged case, we have studied solutions in \(d = 5\) and \( d = 6\) separately and showed that, up to some constraints, the critical behaviors appear only in the spherical topology.
References
S. Hawking, D.N. Page, Thermodynamics of black holes in Anti-de Sitter Space. Commun. Math. Phys. 83, 577 (1987)
D. Kastor, S. Ray, J. Traschen, Enthalpy and the mechanics of AdS black holes. Class. Quant. Grav. 261, 95011 (2009). arXiv:0904.2765
O. Miskovic, R. Olea, Quantum statistical relation for black holes in nonlinear electrodynamics coupled to Einstein–Gauss–Bonnet AdS gravity. Phys. Rev. D 83, 064017 (2011). arXiv:1012.4867
A. Chamblin, R. Emparan, C. Johnson, R. Myers, Charged AdS black holes and catastrophic holography. Phys. Rev. D 60, 064018 (1999)
A. Chamblin, R. Emparan, C. Johnson, R. Myers, Holography, thermodynamics, and fluctuations of charged AdS black holes. Phys. Rev. D 60, 104026 (1999)
M. Cvetic, G.W. Gibbons, D. Kubiznak, C.N. Pope, Black hole enthalpy and an entropy inequality for the thermodynamic volume. Phys. Rev. D 84, 024037 (2011). arXiv:1012.2888 [hep-th]
B.P. Dolan, D. Kastor, D. Kubiznak, R.B. Mann, J. Traschen, Thermodynamic Volumes and Isoperimetric Inequalities for de Sitter Black Holes. arXiv:1301.5926 [hep-th]
B.P. Dolan, Pressure and volume in the first law of black hole thermodynamics. Class. Quant. Grav. 28, 235017 (2011). arXiv:1106.6260 [gr-qc]
D. Kubiznak, R.B. Mann, P–V criticality of charged AdS black holes. J. High Energy Phys. 1207, 033 (2012)
C. Song-Bai, L. Xiao-Fang, L. Chang-Qing, \(P\)–\(V\) criticality of an AdS black hole in f(R) gravity. Chin. Phys. Lett. 30, 060401 (2013)
D. O’Connor, B.P. Dolan, M. Vachovski, Critical behaviour of the fuzzy sphere. arXiv:1308.6512
B.P. Dolan, The compressibility of rotating black holes in D-dimensions. arXiv:1308.5403
S. Gunasekaran, D. Kubiznak, R.B. Mann, Extended phase space thermodynamics for charged and rotating black holes and Born-Infeld vacuum polarization. arXiv:1208.6251v2 [hep-th]
A. Belhaj, M. Chabab, H. El Moumni, L. Medari, M.B. Sedra, The thermodynamical behaviors of Kerr–Newman AdS black holes. Chin. Phys. Lett. 30, 090402 (2013)
A. Belhaj, M. Chabab, H. El Moumni, K. Masmar, M.B. Sedra, Critical behaviors of 3D black holes with a scalar hair. arXiv:1306.2518 [hep-th]
Z. De-Cheng, L. Yunqi, W. Bin, Critical behavior of charged Gauss–Bonnet AdS black holes in the grand canonical ensemble. arXiv:1404.5194 [hep-th]
R. Banerjee, S.K. Modak, D. Roychowdhury, A unified picture of phase transition: from liquid–vapour systems to AdS black holes. J. High Energy Phys. 1210, 125 (2012)
E. Spallucci, A. Smailagic, Maxwell’s equal area law for charged Anti-deSitter black holes. Phys. Lett. B 723, 436 (2013). arXiv:1305.3379 [hep-th]
E. Spallucci, A. Smailagic, Maxwell’s equal area law and the Hawking–Page phase transition. J. Grav. 2013, 525696 (2013). arXiv:1310.2186 [hep-th]
J.X. Zhao, M.S. Ma, L.C. Zhang, H.H. Zhao, R. Zhao, The equal area law of asymptotically AdS black holes in extended phase space. Astrophys. Space Sci. 352, 763 (2014)
A. Belhaj, M. Chabab, H. El Moumni, M.B. Sedra, On thermodynamics of AdS black holes in arbitrary dimensions. Chin. Phys. Lett. 29(10), 100401 (2012)
D.G. Boulware, S. Deser, String generated gravity models. Phys. Rev. Lett. 55, 2656 (1985)
W. Xu, L. Zhao, Critical phenomena of static charged AdS black holes in conformal gravity. Phys. Lett. B 736, 214 (2014). arXiv:1405.7665 [gr-qc]
H. Xu, W. Xu, L. Zhao, Extended phase space thermodynamics for third order Lovelock black holes in diverse dimensions. Eur. Phys. J. C 74(9), 3074 (2014). arXiv:1405.4143 [gr-qc]
H.H. Zhao, L.C. Zhang, M.S. Ma, R. Zhao, Phase transition and clapeyon equation of black hole in higher dimensional AdS spacetime. arXiv:1411.3554 [hep-th]
S.W. Wei, Y.X. Liu, Clapeyron equations and fitting formula of the coexistence curve in the extended phase space of the charged AdS black holes. arXiv:1411.5749 [hep-th]
H.H. Zhao, L.C. Zhang, M.S. Ma, R. Zhao, Two phase equilibrium in charged topological dilaton AdS black hole. arXiv:1411.7202 [gr-qc]
R.G. Cai, L.M. Cao, L. Li, R.Q. Yang, P–V criticality in the extended phase space of Gauss-Bonnet black holes in AdS space. JHEP 1309, 005 (2013). arXiv:1306.6233 [gr-qc]
R.-G. Cai, Gauss–Bonnet black holes in AdS spaces. Phys. Rev. D 65, 084014 (2002). hep-th/0109133
S.H. Hendi, S. Panahiyan, E. Mahmoudi, Thermodynamic analysis of topological black holes in Gauss-Bonnet gravity with nonlinear source. Eur. Phys. J. C 74(10), 3079 (2014). arXiv:1406.2357 [gr-qc]
W. Xu, H. Xu, L. Zhao, Gauss–Bonnet coupling constant as a free thermodynamical variable and the associated criticality. Eur. Phys. J. C 74, 2970 (2014). arXiv:1311.3053 [gr-qc]
D.L. Wiltshire, Spherically symmetric solutions of Einstein–Maxwell theory with a Gauss–Bonnet term. Phys. Lett. B 169, 36 (1986)
M. Cvetic, S. Nojiri, S.D. Odintsov, Black hole thermodynamics and negative entropy in de Sitter and anti-de Sitter Einstein–Gauss–Bonnet gravity. Nucl. Phys. B 628, 295 (2002). hep-th/0112045
D. Kastor, S. Ray, J. Traschen, Smarr formula and an extended first law for Lovelock gravity. Class. Quant. Grav. 27, 235014 (2010). arXiv:1005.5053 [hep-th]
T. Clunan, S.F. Ross, D.J. Smith, On Gauss–Bonnet black hole entropy. Class. Quant. Grav. 21, 3447 (2004). gr-qc/0402044
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Funded by SCOAP3 / License Version CC BY 4.0.
About this article
Cite this article
Belhaj, A., Chabab, M., El moumni, H. et al. Maxwell’s equal-area law for Gauss–Bonnet–Anti-de Sitter black holes. Eur. Phys. J. C 75, 71 (2015). https://doi.org/10.1140/epjc/s10052-015-3299-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-015-3299-7