$B-S$ transition form-factors with the light-cone QCD sum rules

Abstract

In the article, we assume the two scalar nonet mesons below and above 1 GeV are all $\bar{q}q$ states, in case I, the scalar mesons below 1 GeV are the ground states, in case II, the scalar mesons above 1 GeV are the ground states. We calculate the $B-S$ form-factors by taking into account the perturbative ${\mathcal {O}}(\alpha _s)$ corrections to the twist-2 terms using the light-cone QCD sum rules and fit the numerical values of the form-factors into the single-pole forms, which have many phenomenological applications.

1 Introduction

The underlying structures of the scalar mesons are not well established theoretically, there are many candidates with the quantum numbers $J^{PC}=0^{++}$ below $2\,\mathrm {GeV}$, which cannot be accommodated in one $\bar{q}q$ nonet. Roughly speaking, they can be calcified into two nonets, the nonet $\{f_0(600)$, $a_0(980)$, $\kappa (800)$, $f_0(980) \}$ below 1 GeV and the nonet $\{f_0(1370)$, $a_0(1450)$, $K^*_0(1430)$, $f_0(1500) \}$ above 1 GeV. A prospective picture suggests that the scalar mesons above 1 GeV can be assign to be a conventional $\bar{q}q$ nonet with some possible glue components, while the scalar mesons below 1 GeV form an exotic $[qq]_{\bar{3}}[\bar{q}\bar{q}]_{3}$ nonet with substantial mixings with the $q\bar{q}$ states, meson-meson states and glueballs [1]. In the hadronic dressing mechanism, the scalar mesons below 1 GeV have small $\bar{q}q$ cores of typical $\bar{q}q$ meson size, strong couplings to the intermediate hadronic states enrich the pure $\bar{q}q$ states with other components and spend part of their lifetime as virtual meson-meson states [2]. All the existing pictures have both advantages and shortcomings in one way or another. In this article, we assume that the scalar mesons are all $\bar{q}q$ states, in case I, the scalar mesons below 1 GeV are the ground states, in case II, the scalar mesons above 1 GeV are the ground states; and study the $B-S$ transition form-factors with the light-cone QCD sum rules (LCSR) [3–5].

The transition form-factors in the semi-leptonic decays not only depend on the dynamics of strong interactions among the quarks in the initial and final mesons, but also depend on the structures of the involved mesons. They are highly nonperturbative quantities. In the region small-recoil, where the momentum transfer squared $q^2$ is large, the form-factors are dominated by the soft dynamics, while in the large-recoil region, where $q^2 \rightarrow 0$, the form-factors are dominated by the short-distance dynamics.

In the light-cone QCD sum rules, we carry out the operator product expansion near the light-cone $x^2\approx 0$ in stead of the short distance $x\approx 0$, the nonperturbative hadronic matrix elements are parameterized by the light-cone distribution amplitudes (LCDAs) of increasing twist instead of the vacuum condensates [3–5]. Based on the quark-hadron duality, we can obtain copious information about the hadronic parameters at the phenomenological side. The transition form-factors from the LCSR not only have an estimable region of $q^2$, but also embody as many long-distance effects as possible involved in the decaying processes. The operator product expansion is valid at small and intermediate momentum transfer squared $q^2$, $0\le q^2 \le (m_b-m_S)^2-2(m_b-m_S)\chi$, where the $\chi$ is a typical hadronic scale of roughly 500 MeV and independent of the $b$-quark mass $m_b$.

On the other hand, the semi-leptonic $B$-decays are excellent subjects in studying the CKM matrix elements and CP violations. We can use both the exclusive and inclusive $b \rightarrow u$ transitions to study the CKM matrix element $V_{ub}$. Furthermore, the processes induced by the flavor-changing neutral currents $b \rightarrow s(d)$ provide the most sensitive and stringent test for the standard model at one-loop level and can put powerful constraints on the new physics models, as they are forbidden at the tree-level in the standard model [6–8]. So reliable calculations of the transition form-factors are needed to make robust predictions.

The $B-S$ transition form-factors have been calculated with the LCSR [9–12], the three-point QCD sum rules [13–15], the perturbative QCD [16], the light front quark model [17], etc. In Refs. [9–12], the $B- S$ form-factors are calculated with the LCSR in the leading order approximation, the perturbative ${\mathcal {O}}(\alpha _s)$ corrections are neglected. Due to the lengthy calculations, only perturbative ${\mathcal {O}}(\alpha _s)$ corrections to the twist-2 and twist-3 terms in the LCSR for the $B - P,\, V$ form-factors [18–26] and perturbative ${\mathcal {O}}(\alpha _s^2)$ corrections to the twist-2 terms in the LCSR for the $B -\pi$ form-factor [27] are studied up to now, where the $P$ and $V$ denote the light pseudoscalar and vector mesons, respectively. In this article, we study the $B-S$ form-factors by taking into account the perturbative ${\mathcal {O}}(\alpha _s)$ corrections to the twist-2 terms using the LCSR.

The article is arranged as follows: we derive the LCSR for the $B-S$ form-factors by including the perturbative ${\mathcal {O}}(\alpha _s)$ corrections to the twist-2 terms in Sect. 2; in Sect. 3, we present the numerical results and discussions; and Sect. 4 is reserved for our conclusions.

2 Light-cone QCD sum rules for the form-factors

In the following, we write down the two-point correlation functions $\Pi ^{i}_{\mu }(p,q)$ in the LCSR,

$$\begin{aligned} \begin{aligned} \Pi ^i_{\mu }(p,q)&=i\int d^4x e^{iq \cdot x} \langle S(p)|T\left\{ J^i_{\mu }(x)J_{5}(0)\right\} |0\rangle ,\\ J^A_{\mu }(x)&= \overline{q}(x) \gamma _{\mu }\gamma _5 b(x),\\ J^B_{\mu }(x)&= \overline{q}(x) \sigma _{\mu \nu }\gamma _5q^\nu b(x), \\ J_{ 5}(0)&= m_b\overline{b}(0)i\gamma _5q^{\prime }(0), \end{aligned} \end{aligned}$$

(1)

where $i=A,B$, $q,q^\prime =u,d,s$, the pseudoscalar currents $J_{ 5}(x)$ interpolate the $B_{q^\prime }$ mesons, and the axial-vector currents $J^i_\mu (x)$ induce the $B\rightarrow S$ transitions.

We can insert a complete set of intermediate hadronic states with the same quantum numbers as the current operators $J_{ 5}(0)$ into the correlation functions $\Pi ^{i}_{\mu }(p,q)$ to obtain the hadronic representation [28–30]. After isolating the ground state contributions from the $B_{q^\prime }$ mesons, we get the following result,

$$\begin{aligned} \Pi ^A_{\mu }(p,q)&= \frac{f_{B_{q^\prime }}m_{B_{q^\prime }}^2 \langle S(p)|J^A_{\mu }(0)|B_{q^\prime }(p+q)\rangle }{m_{B_{q^\prime }}^2-(p+q)^2}+\cdots \, ,\nonumber \\&= -\frac{f_{B_{q^\prime }}m_{B_{q^\prime }}^2 }{m_{B_{q^\prime }}^2-(p+q)^2}\left\{ 2iF_{+}(q^2)p_\mu \right. \nonumber \\&\left. +\,i\left[ F_{+}(q^2)+F_{-}(q^2)\right] q_\mu \right\} +\cdots \, , \end{aligned}$$

(2)

$$\begin{aligned} \Pi ^B_{\mu }(p,q)&= \frac{f_{B_{q^\prime }}m_{B_{q^\prime }}^2 \langle S(p)|J^B_{\mu }(0)|B_{q^\prime }(p+q)\rangle }{m_{B_{q^\prime }}^2-(p+q)^2}+\cdots \, ,\nonumber \\&= -\frac{2f_{B_{q^\prime }}m_{B_{q^\prime }}^2 }{\left( m_{B_{q^\prime }}+m_S\right) \left( m_{B_{q^\prime }}^2-(p+q)^2\right) }\nonumber \\&\times \left\{ F_{T}(q^2)\left( q^2p_\mu - q\cdot p q_\mu \right) \right\} +\cdots , \end{aligned}$$

(3)

where the decay constants $f_{B_{q^\prime }}$ and the form-factors $F_{+}(q^2)$, $F_{-}(q^2)$ and $F_{T}(q^2)$ are defined by

$$\begin{aligned} \langle 0|J_{5}(0)|B_{q^\prime }(p+q)\rangle&= f_{B_{q^\prime }}m_{B_{q^\prime }}^2, \nonumber \\ \langle S(p)|J^A_{\mu }(0)|B_{q^\prime }(p+q)\rangle&= -2iF_{+}(q^2)p_\mu \nonumber \\&-i\left[ F_{+}(q^2)+F_{-}(q^2)\right] q_\mu \, , \nonumber \\ \langle S(p)|J^B_{\mu }(0)|B_{q^\prime }(p+q)\rangle&= -\frac{2F_T(q^2)}{m_{B_{q^\prime }}+m_S}\left( q^2p_\mu - q\cdot p q_\mu \right) .\nonumber \\ \end{aligned}$$

(4)

We can also parameterize the form-factors into another form,

$$\begin{aligned}&\langle S(p)|J^A_{\mu }(0)|B_{q^\prime }(p+q)\rangle \!=\!-i\left[ F_{1}(q^2)\left( P_\mu -\frac{m^2_{B_{q^\prime }}-m_S^2}{q^2}q_\mu \right) \right. \nonumber \\&\qquad \left. +F_{0}(q^2)\frac{m^2_{B_{q^\prime }}-m_S^2}{q^2}q_\mu \right] , \end{aligned}$$

(5)

where $P=2p+q$ and

$$\begin{aligned}&F_{1}(q^2)=F_{+}(q^2)\, , \nonumber \\&F_{0}(q^2)=F_{+}(q^2)+\frac{q^2}{m^2_{B_{q^\prime }}-m_S^2}F_{-}(q^2)\, . \end{aligned}$$

(6)

We carry out the operator product expansion for the correlation functions $\Pi ^i_{\mu }(p,q)$ in the large space-like momentum region $(p+q)-m_b^2\ll 0$ and the large recoil region of the decaying $B_{q^\prime }$-meson, which correspond to the small light-cone distance $x^2\approx 0$ and are required by the validity of the operator product expansion. We contract the $b$-quarks in the correlation functions $\Pi ^i_{\mu }(p,q)$ with Wick’s theorem, then substantiate the free $b$-quark propagator and the corresponding $S$-meson LCDAs into the correlation functions $\Pi ^i_{\mu }(p,q)$ and complete the integrals both in the coordinate space and momentum space to obtain

$$\begin{aligned}&\Pi ^A_{\mu }(p,q)= im_b^2 \displaystyle \int \nolimits _0^1 du \nonumber \\&\quad \times \left\{ \frac{\phi (u)}{m_b^2-(q+up)^2}p_\mu -\frac{m_S\phi _s(u)}{m_b\left[ m_b^2-(q+up)^2\right] }\right. \nonumber \\&\quad \times \left. (q+up)_\mu \right. \nonumber \\&\quad -\frac{m_S\phi _\sigma (u)}{3m_b}\left[ \frac{1}{m_b^2-(q+up)^2}+\frac{m_b^2}{\left( m_b^2-(q+up)^2\right) ^2} \right] p_\mu \nonumber \\&\quad +\frac{m_S\phi _\sigma (u)}{6m_b}\left. \left[ p_\mu +(q\!+\!up)_\mu \frac{d}{du}\right] \frac{1}{m_b^2-(q\!+\!up)^2}\right\} \!+\!\cdots ,\qquad \end{aligned}$$

(7)

$$\begin{aligned}&\Pi ^B_{\mu }(p,q)= m_b \int _0^1 du \nonumber \\&\quad \times \left\{ \frac{\phi (u)}{m_b^2-(q+up)^2} -\frac{m_Sm_b\phi _\sigma (u)}{3\left[ m_b^2-(q+up)^2\right] ^2}\right\} \nonumber \\&\quad \times \left( q^2p_\mu - q\cdot p q_\mu \right) +\cdots . \end{aligned}$$

(8)

Now we take a short digression to discuss the LCDAs of the related two-quark scalar mesons. Let us write down the definitions for the twist-2 and twist-3 LCDAs $\phi (u,\mu )$, $\phi _s(u,\mu )$ and $\phi _\sigma (u,\mu )$,

$$\begin{aligned}&\langle S(p)|\bar{q}(x)\gamma _\mu q^\prime (y)|0 \rangle = p_\mu \int ^1_0 due^{iup\cdot x+\bar{u}p\cdot y}\phi (u,\mu )\!,\nonumber \\&\langle S(p)|\bar{q}(x)q^\prime (y)|0\rangle = m_S \int _0^1 du \, e^{i(u p\cdot x+ \bar{u}p \cdot y)} \phi _{s}(u,\mu ), \nonumber \\&\langle S(p)|\bar{q}(x) \sigma _{\mu \nu } q^\prime (y)|0\rangle \nonumber \\&\quad = -m_{S}(p_{\mu }z_{\nu } -p_{\nu }z_{\mu }) \int _0^1 du \, e^{i(u p\cdot x+ \bar{u}p \cdot y)} \frac{\phi _{\sigma }(u,\mu )}{6},\nonumber \\ \end{aligned}$$

(9)

where the $u$ is the fraction of the light-cone momentum of the scalar meson carried by the $q$-quark, $\bar{u}=1-u$ and $z=x-y$. The LCDAs $\phi (u,\mu )$, $\phi _s(u,\mu )$ and $\phi _\sigma (u,\mu )$ can be expanded into a series of Gegenbauer polynomials $C^{1/2(3/2)}_{m}(u-\bar{u})$ with increasing conformal spin according to the conformal symmetry of the QCD,

$$\begin{aligned}&\phi (u,\mu )\!=\!\bar{f}_S(\mu )6u\bar{u}\left[ B_0(\mu )+\sum _{m=1}^{\infty }B_m(\mu )C^{3/2}_m (2u-1)\right] , \nonumber \\&\phi _s(u,\mu )\!=\!\bar{f}_S(\mu )\left[ 1+\sum _{m=1}^{\infty }B^s_m(\mu )C^{1/2}_m (2u-1)\right] , \nonumber \\&\phi _\sigma (u,\mu )\!=\!\bar{f}_S(\mu )6u\bar{u}\left[ 1+\sum _{m=1}^{\infty }B^\sigma _m(\mu )C^{3/2}_m (2u-1)\right] ,\nonumber \\ \end{aligned}$$

(10)

where the $B_m(\mu )$, $B^s_m(\mu )$ and $B_m^\sigma (\mu )$ are the Gegenbauer moments [5, 31, 32]. The twist-2 LCDA is antisymmetric under the interchange $u\leftrightarrow \bar{u}$ in the flavor $SU(3)$ symmetry limit, and the zeroth Gegenbauer moment $B_0$ vanishes in the flavor $SU(3)$ symmetry limit, the odd Gegenbauer moments are dominant. In this article, we take into account the first two odd moments $B_1$ and $B_3$ and set $B^s_m=B^\sigma _m=0$ [33].

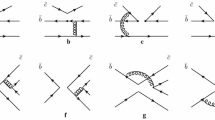
Then we calculate the perturbative ${\mathcal {O}}(\alpha _s)$ contributions to the twist-2 terms, while the perturbative ${\mathcal {O}}(\alpha _s)$ corrections to the twist-3 terms are beyond the present work, as the contributions of the twist-3 terms are suppressed by the factor $m_S/m_b$ (or $m_bm_S/M^2$ after the Borel transformation) and play a less important role, see Eqs. (7–8). The six Feynman diagrams which determine the perturbative ${\mathcal {O}}(\alpha _s)$ corrections are shown explicitly in Fig. 1. For simplicity, we perform the calculations in the Feynman gauge, introduce convenient dimensionless variables $r_1 = q^2/m_b^2$, $r_2=(p+q)^2/m_b^2$ (or $s/m_b^2$), $\rho =r_1+u(r_2-r_1)$, and take the approximation $m_S^2/m_b^2\approx 0$. In calculations, we regularize both the ultraviolet and collinear (or infrared) divergences with dimensional regularization by setting $D=4-2\varepsilon _\mathrm{UV}=4+2\varepsilon _\mathrm{IR}$, and perform the renormaliztion in the $\overline{MS}$ scheme with totally anti-commuting $\gamma _5$. In the following, we write down the contributions of the diagrams $a$, $b$, $c$, $d$, $e$ and $f$, respectively,

$$\begin{aligned}&\Pi _\mu ^{A,a}(p,q)=-\frac{C_Fg_s^2m_b}{4} \int \frac{d^Dk}{(2\pi )^D}\int _0^1 du\frac{\phi (u)}{k^2}\nonumber \\&\quad \!\times \left\{ \not \!p \gamma ^\lambda \frac{{\not \!k}+u{\not \!p}}{(k+up)^2} \gamma _\mu \gamma _5\frac{{\not \!k}+\not \!q+u{\not \!p}+m_b}{(k+q+up)^2-m_b^2} \gamma _5 \frac{{\not \!k}-\bar{u}{\not \!p}}{(k\!-\!\bar{u}p)^2}\gamma _\lambda \right\} \!,\nonumber \\&=-\frac{iC_F\alpha _s }{2\pi } \int _0^1 du \phi (u) \left\{ \left[ \frac{\log (1-r_2)}{r_2}-\frac{\log (1-r_1)}{r_1}\right] q_\mu \right. \nonumber \\&\quad +\left[ \frac{u}{1-r_1}+\frac{\bar{u}}{1-r_2}+\frac{\log (1-r_2)-\log (1-r_1)}{r_2-r_1} \right] \nonumber \\&\quad \times \left( \frac{1}{\hat{\varepsilon }_\mathrm{IR}}+\log \frac{m_b^2}{\mu ^2}\right) p_\mu \nonumber \\&\quad \left. +\left[ \frac{G(r_2)-G(r_1)}{r_2-r_1}+\frac{\log (1-r_2)}{r_2}+u\frac{2\log (1-r_1)+1}{1-r_1}\right. \right. \nonumber \\&\quad \left. \left. +\,\bar{u}\frac{2\log (1-r_2)+1}{1-r_2}\right] p_\mu \right\} , \end{aligned}$$

(11)

$$\begin{aligned}&\Pi _\mu ^{A,b+c}(p,q)=-\frac{C_Fg_s^2m_b}{4} \int \frac{d^Dk}{(2\pi )^D}\int _0^1 du\frac{\phi (u)}{k^2}\nonumber \\&\quad \times \left\{ \not \!p \gamma ^\lambda \frac{{\not \!k}+u{\not \!p}}{(k+up)^2} \gamma _\mu \gamma _5\frac{{\not \!k}+\not \!q+u{\not \!p}+m_b}{(k+q+up)^2-m_b^2}\gamma _\lambda \frac{{\not \!q}+u{\not \!p}+m_b}{(q+up)^2-m_b^2} \gamma _5 \right. \nonumber \\&\quad \left. + {\not \!p} \gamma _\mu \gamma _5 \frac{{\not \!q}+u{\not \!p}+m_b}{(q+up)^2-m_b^2}\gamma ^\lambda \frac{{\not \!k}+\not \!q+u{\not \!p}+m_b}{(k+q+up)^2-m_b^2}\gamma _5\right. \nonumber \\&\quad \times \left. \frac{{\not \!k}-\bar{u}{\not \!p}}{(k-\bar{u}p)^2} \gamma _\lambda \right\} ,\nonumber \\&=\frac{iC_F\alpha _s }{2\pi } \int _0^1 du \frac{\phi (u)}{1-\rho } \left\{ -\frac{1}{2u} \left[ \frac{(1-\rho )F(\rho )}{\rho ^2}-\frac{(1-r_1)F(r_1)}{r_1^2}\right] q_\mu \right. \nonumber \\&\quad +\left[ \frac{F(\rho )-F(r_1)}{u(r_2-r_1)}-\frac{F(\rho )-F(r_2)}{\bar{u}(r_2-r_1)}+2\log (1-\rho )\right] \nonumber \\&\quad \times \left( \frac{1}{\hat{\varepsilon }_\mathrm{IR}}+\log \frac{m_b^2}{\mu ^2}\right) p_\mu \nonumber \\&\quad +\left[ \frac{5}{2}\left( \frac{1}{\hat{\varepsilon }_\mathrm{UV}}-\log \frac{m_b^2}{\mu ^2}\right) -\frac{(1-\rho )F(\rho )}{2\rho ^2}\right. \nonumber \\&\quad \left. +2\log ^2(1-\rho )+2\mathrm{Li_2(\rho )}+3+\frac{F(\rho )}{\rho } +\frac{F(r_2)}{r_2}\right] p_\mu \nonumber \\&\quad +\left[ \frac{(1-\rho )G(\rho )-(1-r_1)G(r_1)-2F(\rho )+2F(r_1)}{u(r_2-r_1)}\right. \nonumber \\&\quad \left. \left. -\frac{(1-\rho )G(\rho )\!-\!(1\!-\!r_2)G(r_2)\!-\!2F(\rho )+2F(r_2)}{\bar{u}(r_2-r_1)}\right] p_\mu \right\} , \end{aligned}$$

(12)

$$\begin{aligned}&\Pi _\mu ^{A,d}(p,q)=-\frac{C_Fg_s^2m_b}{4} \int \frac{d^Dk}{(2\pi )^D}\int _0^1 du\frac{\phi (u)}{k^2}\nonumber \\&\quad \times \left\{ \not \!p \gamma _\mu \gamma _5 \frac{{\not \!q}+u{\not \!p}+m_b}{(q+up)^2-m_b^2}\gamma ^\lambda \frac{{\not \!k}+\not \!q+u{\not \!p}+m_b}{(k+q+up)^2-m_b^2}\gamma _\lambda \right. \nonumber \\&\quad \left. \times \frac{{\not \!q}+u{\not \!p}+m_b}{(q+up)^2-m_b^2}\gamma _5 \right\} \, ,\nonumber \\&=-\frac{iC_F\alpha _s }{2\pi } \int _0^1 du \frac{\phi (u)\rho }{(1-\rho )^2} \left\{ \frac{1}{\hat{\varepsilon }_\mathrm{UV}}-\log \frac{m_b^2}{\mu ^2}\right. \nonumber \\&\quad \left. +1-\frac{(1-\rho )F(\rho )}{\rho ^2} \right\} p_\mu , \end{aligned}$$

(13)

$$\begin{aligned}&\Pi _\mu ^{A,e+f}(p,q)=-\frac{C_Fg_s^2m_b}{4} \int \frac{d^Dk}{(2\pi )^D}\int _0^1 du\frac{\phi (u)}{k^2}\nonumber \\&\quad \times \left\{ {\not \!p} \gamma ^\lambda \frac{{\not \!k}+u{\not \!p}}{(k+up)^2} \gamma _\lambda \frac{u{\not \!p}}{(up)^2}\gamma _\mu \gamma _5\frac{\not \!q+u{\not \!p}+m_b}{(q+up)^2-m_b^2} \gamma _5 \right. \nonumber \\&\quad \left. +{\not \!p} \gamma _\mu \gamma _5\frac{\not \!q+u{\not \!p}+m_b}{(q+up)^2-m_b^2} \gamma _5 \frac{-\bar{u}{\not \!p}}{(-\bar{u}p)^2} \gamma ^\lambda \frac{{\not \!k}-\bar{u}{\not \!p}}{(k-\bar{u}p)^2}\gamma _\lambda \right\} \, ,\nonumber \\&\quad \propto \frac{1}{\varepsilon _\mathrm{UV}}-\frac{1}{\varepsilon _\mathrm{IR}}, \end{aligned}$$

(14)

$$\begin{aligned}&\Pi _\mu ^{B,a}(p,q)=-\frac{C_Fg_s^2m_b}{4} \int \frac{d^Dk}{(2\pi )^D}\int _0^1 du\frac{\phi (u)}{k^2}\nonumber \\&\quad \times \left\{ \not \!p \gamma ^\lambda \frac{{\not \!k}+u{\not \!p}}{(k+up)^2} \sigma _{\mu \nu }\gamma _5q^\nu \frac{{\not \!k}+\not \!q+u{\not \!p}+m_b}{(k+q+up)^2-m_b^2} \gamma _5\right. \nonumber \\&\left. \quad \times \frac{{\not \!k}-\bar{u}{\not \!p}}{(k-\bar{u}p)^2}\gamma _\lambda \right\} ,\nonumber \\&\quad =-\frac{C_F\alpha _s }{2\pi m_b} \int _0^1 du \frac{\phi (u)}{1-\rho }\left\{ \left[ \frac{u}{1-r_1}+\frac{\bar{u}}{1-r_2}\right. \right. \nonumber \\&\quad \left. \left. \quad +\frac{\log (1-r_2)-\log (1-r_1)}{r_2-r_1} \right] \right. \nonumber \\&\qquad \times \left( \frac{1}{\hat{\varepsilon }_\mathrm{IR}}+\log \frac{m_b^2}{\mu ^2}\right) +\frac{G(r_2)-G(r_1)}{r_2-r_1}+\frac{1}{r_2-r_1}\nonumber \\&\qquad \times \left[ \frac{F(r_2)}{r_2}-\frac{F(r_1)}{r_1}\right] \nonumber \\&\left. \qquad +\frac{u\log (1-r_1)}{r_1}+\frac{\bar{u}\log (1-r_2)}{r_2} +u\frac{2\log (1-r_1)+1}{1-r_1}\right. \nonumber \\&\left. \qquad +\bar{u}\frac{2\log (1-r_2)+1}{1-r_2} \right\} \left( q^2p_\mu - q\cdot p q_\mu \right) , \end{aligned}$$

(15)

$$\begin{aligned}&\Pi _\mu ^{B,b+c}(p,q)=-\frac{C_Fg_s^2m_b}{4} \int \frac{d^Dk}{(2\pi )^D}\int _0^1 du\frac{\phi (u)}{k^2}\nonumber \\&\quad \times \left\{ \not \!p \gamma ^\lambda \frac{{\not \!k}+u{\not \!p}}{(k+up)^2} \sigma _{\mu \nu }\gamma _5q^\nu \frac{{\not \!k}+\not \!q+u{\not \!p}+m_b}{(k+q+up)^2-m_b^2}\gamma _\lambda \right. \nonumber \\&\left. \quad \times \frac{{\not \!q}+u{\not \!p}+m_b}{(q+up)^2-m_b^2} \gamma _5 \right. \nonumber \\&\left. \quad + {\not \!p} \sigma _{\mu \nu }\gamma _5q^\nu \frac{{\not \!q}+u{\not \!p}+m_b}{(q+up)^2-m_b^2}\gamma ^\lambda \frac{{\not \!k}+\not \!q+u{\not \!p}+m_b}{(k+q+up)^2-m_b^2}\gamma _5\right. \nonumber \\&\left. \quad \times \frac{{\not \!k}-\bar{u}{\not \!p}}{(k-\bar{u}p)^2} \gamma _\lambda \right\} ,\nonumber \\&=\frac{C_F\alpha _s }{2\pi m_b} \int _0^1 du \frac{\phi (u)}{1-\rho } \left\{ \left[ \frac{F(\rho )-F(r_1)}{u(r_2-r_1)}\right. \right. \nonumber \\&\quad \left. \left. -\frac{F(\rho )-F(r_2)}{\bar{u}(r_2-r_1)}+2\log (1-\rho )\right] \right. \nonumber \\&\quad \times \left( \frac{1}{\hat{\varepsilon }_\mathrm{IR}}+\log \frac{m_b^2}{\mu ^2}\right) +\left[ 2\left( \frac{1}{\hat{\varepsilon }_\mathrm{UV}}-\log \frac{m_b^2}{\mu ^2}\right) \right. \nonumber \\&\quad \left. +2\log ^2(1-\rho )+2\mathrm{Li_2(\rho )}+3\right. \nonumber \\&\left. \quad +\frac{2F(\rho )}{\rho } \right] +\frac{1}{u(r_2-r_1)}\left[ \frac{F(\rho )}{\rho }-\frac{F(r_1)}{r_1} \right] \nonumber \\&\quad +\frac{1}{\bar{u}(r_2-r_1)}\left[ \frac{F(\rho )}{\rho }-\frac{F(r_2)}{r_2} \right] \nonumber \\&\quad +\left[ \frac{(1-\rho )G(\rho )-(1-r_1)G(r_1)-3F(\rho )+3F(r_1)}{u(r_2-r_1)}\right. \nonumber \\&\left. \left. \quad -\frac{(1-\rho )G(\rho )-(1-r_2)G(r_2)-F(\rho )+F(r_2)}{\bar{u}(r_2-r_1)}\right] \right\} \nonumber \\&\quad \times \left( q^2p_\mu - q\cdot p q_\mu \right) , \end{aligned}$$

(16)

$$\begin{aligned}&\Pi _\mu ^{B,d}(p,q)=-\frac{C_Fg_s^2m_b}{4} \int \frac{d^Dk}{(2\pi )^D}\int _0^1 du\frac{\phi (u)}{k^2}\nonumber \\&\quad \times \left\{ \not \!p \sigma _{\mu \nu }\gamma _5q^\nu \frac{{\not \!q}+u{\not \!p}+m_b}{(q+up)^2-m_b^2}\gamma ^\lambda \frac{{\not \!k}+\not \!q+u{\not \!p}+m_b}{(k+q+up)^2-m_b^2}\gamma _\lambda \right. \nonumber \\&\left. \times \frac{{\not \!q}+u{\not \!p}+m_b}{(q+up)^2-m_b^2}\gamma _5 \right\} ,\nonumber \\&= -\frac{C_F\alpha _s }{4\pi m_b} \int _0^1 du \frac{\phi (u)}{(1-\rho )^2} \left\{ (7-\rho )\left[ \frac{1}{\hat{\varepsilon }_\mathrm{UV}}-\log \frac{m_b^2}{\mu ^2}+\frac{F(\rho )}{\rho }\right] \right. \nonumber \\&\left. +4-\frac{(1+\rho )F(\rho )}{\rho ^2} \right\} \left( q^2p_\mu - q\cdot p q_\mu \right) \, , \end{aligned}$$

(17)

$$\begin{aligned}&\Pi _\mu ^{B,e+f}(p,q)=-\frac{C_Fg_s^2m_b}{4} \int \frac{d^Dk}{(2\pi )^D}\int _0^1 du\frac{\phi (u)}{k^2}\nonumber \\&\quad \times \left\{ {\not \!p} \gamma ^\lambda \frac{{\not \!k}+u{\not \!p}}{(k+up)^2} \gamma _\lambda \frac{u{\not \!p}}{(up)^2}\sigma _{\mu \nu }\gamma _5q^\nu \frac{\not \!q+u{\not \!p}+m_b}{(q+up)^2-m_b^2} \gamma _5 \right. \nonumber \\&\left. \quad +{\not \!p} \sigma _{\mu \nu }\gamma _5q^\nu \frac{\not \!q+u{\not \!p}+m_b}{(q+up)^2-m_b^2} \gamma _5 \frac{-\bar{u}{\not \!p}}{(-\bar{u}p)^2} \gamma ^\lambda \frac{{\not \!k}-\bar{u}{\not \!p}}{(k-\bar{u}p)^2}\gamma _\lambda \right\} \, ,\nonumber \\&\propto \frac{1}{\varepsilon _\mathrm{UV}}-\frac{1}{\varepsilon _\mathrm{IR}}, \end{aligned}$$

(18)

where

$$\begin{aligned} \frac{1}{\hat{\varepsilon }_\mathrm{UV}}&= \frac{1}{\varepsilon _\mathrm{UV}}-\gamma _E+\log 4\pi , \nonumber \\ \frac{1}{\hat{\varepsilon }_\mathrm{IR}}&= \frac{1}{\varepsilon _\mathrm{IR}}+\gamma _E-\log 4\pi , \nonumber \\ F(\rho )&= (1-\rho )\log (1-\rho )+\rho ,\nonumber \\ G(\rho )&= \log ^2(1-\rho )+\mathrm{Li_2}(\rho )+\log (1-\rho ), \end{aligned}$$

(19)

$\mathrm{Li_2}(x)=-\int _0^x dt \frac{\log (1-t)}{t}$ and $C_F=\frac{4}{3}$. The terms proportional to the ultraviolet divergence $\frac{1}{\hat{\varepsilon }_\mathrm{UV}}$ are eliminated through renormalization, while the terms proportional to the infrared (or collinear) divergence $\frac{1}{\hat{\varepsilon }_\mathrm{IR}}+\log \frac{m_b^2}{\mu ^2}$ are absorbed in the twist-2 LCDA $\phi (u,\mu )$. The terms proportional to $\frac{1}{\bar{u}}$ are potentially divergent at the end point $u=1$ after performing the quark-hadron duality, we absorb those terms into the twist-2 LCDA $\phi (u,\mu )$. We introduce the notations $\widetilde{\Pi }_\mu ^{A,\alpha _s}(p,q)$, $\widetilde{\Pi }_\mu ^{B,\alpha _s}(p,q)$, $\widetilde{\Pi }_\mu ^{A,a,b,c,d}(p,q)$, $\widetilde{\Pi }_\mu ^{B,a,b,c,d}(p,q)$, $\widetilde{\Pi }_{+}(q^2,(p+q)^2)$, $\widetilde{\Pi }_{+-}(q^2,(p+q)^2)$, $\widetilde{\Pi }_{T}(q^2,(p+q)^2)$ to denote the renormalized correlation functions,

$$\begin{aligned} \widetilde{\Pi }_\mu ^{A,\alpha _s}(p,q)&= \widetilde{\Pi }_\mu ^{A,a}(p,q)+\widetilde{\Pi }_\mu ^{A,b+c}(p,q)+\widetilde{\Pi }_\mu ^{A,d}(p,q)\, ,\nonumber \\&= \widetilde{\Pi }_{+}(q^2,(p+q)^2)p_\mu \!+\!\widetilde{\Pi }_{+-}(q^2,(p+q)^2)q_\mu ,\nonumber \\ \widetilde{\Pi }_\mu ^{B,\alpha _s}(p,q)&= \widetilde{\Pi }_\mu ^{B,a}(p,q)+\widetilde{\Pi }_\mu ^{B,b+c}(p,q)+\widetilde{\Pi }_\mu ^{B,d}(p,q)\, ,\nonumber \\&= \widetilde{\Pi }_{T}(q^2,(p+q)^2)\left( q^2p_\mu -q\cdot p q_\mu \right) \, . \end{aligned}$$

(20)

Then we obtain the QCD spectral densities through the dispersion relation,

$$\begin{aligned} \widetilde{\Pi }_{i}(q^2,(p+q)^2)&= \int _{m_b^2}^{s_0}ds \frac{\rho _{i}^{\alpha _s}(s)}{s-(p+q)^2}\nonumber \\&+\int _{s_0}^{\infty }ds \frac{\rho _{i}^{\alpha _s}(s)}{s-(p+q)^2}\, , \end{aligned}$$

(21)

where $i=+,+-,T$ and

$$\begin{aligned}&\rho _{+}^{\alpha _s}(s)=\frac{\mathrm{Im }\widetilde{\Pi }_{+}(q^2,s)}{\pi }, \nonumber \\&\quad =\frac{C_F\alpha _s}{2\pi }\int _{\bar{\Delta }}^1 du \phi (u)\left\{ \frac{1}{r_2}+\frac{2\bar{u}}{1-r_2}\right. \nonumber \\&\left. \quad -\frac{\log r_2-2\log (r_2-1)-1}{r_2-r_1}\right. \nonumber \\&\quad +\Theta (\rho -1)\left[ \frac{1-\rho }{2\rho ^2}-\frac{4\log (\rho -1)}{1-\rho }\mid _{+} +\frac{2\log \rho }{1-\rho }\mid _{+}\right. \nonumber \\&\left. \quad -\frac{2}{\rho }-\frac{1-r_2}{r_2}\frac{1}{1-\rho }\mid _{+} \right. \nonumber \\&\left. \quad +\frac{\log \rho +1-2\log (\rho -1)}{u(r_2-r_1)} \right] \nonumber \\&\quad +\Theta (1-\rho )\left[ -\frac{1-r_2}{r_2}\frac{1}{1-\rho }\mid _{+} \right] \nonumber \\&\quad +\delta (1-\rho ) \left[ -\frac{5}{2}\log \frac{m_b^2}{\mu ^2} +2\log ^2(r_2-1)\right. \nonumber \\&\quad \left. +2\mathrm{Li_2}(1-r_2) -\frac{\pi ^2}{3}+6\right. \nonumber \\&\quad +\frac{1-r_2}{r_2}\left[ 2\log (r_2-1)-\log (1-r_1)\right] \nonumber \\&\quad +\left( 1-\log \frac{m_b^2}{\mu ^2} \right) \left( 1+\frac{1}{r_2-r_1}\frac{\overleftarrow{d}}{du}\right) \nonumber \\&\left. \left. \quad +\frac{2F(r_1)-(1-r_1)G(r_1)-2}{u(r_2-r_1)}\right] \right\} \, , \end{aligned}$$

(22)

$$\begin{aligned}&\rho _{+-}^{\alpha _s}(s)=\frac{\mathrm{Im }\widetilde{\Pi }_{+-}(q^2,s)}{\pi }, \nonumber \\&\quad =\frac{C_F\alpha _s}{2\pi }\int _{\bar{\Delta }}^1 du \phi (u)\nonumber \\&\qquad \times \left\{ \frac{1}{r_2}-\Theta (\rho -1) \frac{\rho -1}{2u\rho ^2} +\delta (1-\rho )\frac{(1-r_1)F(r_1)}{2ur_1^2}\right\} ,\nonumber \\ \end{aligned}$$

(23)

$$\begin{aligned}&\rho _{T}^{\alpha _s}(s)=\frac{\mathrm{Im }\widetilde{\Pi }_{T}(q^2,s)}{\pi }, \nonumber \\&\quad =\frac{C_F\alpha _s}{2\pi m_b}\int _{\bar{\Delta }}^1 du \phi (u)\left\{ \frac{2\log (r_2-1)-\log r_2+1}{r_2-r_1} \right. \nonumber \\&\qquad \left. -\frac{r_2-1}{r_2(r_2-r_1)}+\frac{\bar{u}}{r_2}+\frac{2\bar{u}}{1-r_2}\right. \nonumber \\&\qquad +\Theta (\rho -1)\left[ -\frac{3}{2\rho }-\frac{4\log (\rho -1)}{1-\rho }\mid _{+}\right. \nonumber \\&\qquad \left. +\frac{2\log \rho }{1-\rho }\mid _{+} +\frac{\log \rho -2\log (\rho -1)-1}{u(r_2-r_1)}\right. \nonumber \\&\qquad \left. +\left( 3-\frac{1}{\rho } \right) \frac{1}{u(r_2-r_1)}+\frac{5\rho -1}{2\rho ^2}\frac{1}{1-\rho }\mid _{+} \right] \nonumber \\&\qquad +\delta (1-\rho )\left[ \frac{9}{2}-\frac{\pi ^2}{3}+2\log ^2(r_2-1)\right. \nonumber \\&\qquad +2\mathrm{Li_2}(1-r_2)-\frac{3}{2}\log \frac{m_b^2}{\mu ^2}\nonumber \\&\qquad +\left( 3F(r_1)-(1-r_1)G(r_1)-2-\frac{F(r_1)}{r_1} \right) \frac{1}{u(r_2-r_1)} \nonumber \\&\qquad \left. \left. -2\log (r_2-1)-3\log \frac{m_b^2}{\mu ^2}\frac{1}{r_2-r_1}\overleftarrow{\frac{d}{du}}\right. \right. \nonumber \\&\qquad \left. \left. +\frac{9}{2}\frac{1}{r_2-r_1}\overleftarrow{\frac{d}{du}}- \frac{1}{2\rho }\frac{1}{r_2-r_1}\overleftarrow{\frac{d}{du}} \right] \right\} \, , \end{aligned}$$

(24)

$\bar{\Delta }=\frac{m_b^2-q^2}{s_0-q^2}$, $\phi (\rho )\frac{f(\rho )}{1-\rho }\mid _{+}=\frac{f(\rho )}{1-\rho }\left[ \phi (\rho )-\phi (1)\right]$, and $\Theta (x)=1$ for $x\ge 0$, the $\overleftarrow{\frac{d}{du}}$ does not act on the $\delta (1-\rho )$.

Fig. 1

The six Feynman diagrams contribute to the perturbative ${\mathcal {O}}(\alpha _s)$ corrections, they are denoted by $a$, $b$, $c$, $d$, $e$, $f$ sequentially in the text

We take quark-hadron duality below the continuum thresholds $s_0$, and perform the Borel transformation with respect to the variable $P^{\prime 2}=-(p+q)^2$ to obtain the LCSR,

$$\begin{aligned}&F_{+}(q^2)=-\frac{m_b^2}{2f_{B_{q^\prime }}m_{B_{q^\prime }}^2}\exp \left( \frac{m_{B_{q^\prime }}^2}{M^2}\right) \nonumber \\&\quad \times \int _{\Delta }^1du\left\{ \frac{\phi (u)}{u}-\frac{m_S\phi _s(u)}{m_b} -\frac{m_S\phi _\sigma (u)}{3um_b}\left( 1+\frac{m_b^2}{u M^2} \right) \right. \nonumber \\&\quad \left. +\frac{m_S\phi _\sigma (u)}{6um_b}\left( 1+u^2\frac{d}{du} \frac{1}{u}\right) \right\} \exp \left( -\frac{m_b^2+u\bar{u}m_S^2-\bar{u}q^2}{uM^2} \right) \nonumber \\&\quad -\frac{m_b^2}{2f_{B_{q^\prime }}m_{B_{q^\prime }}^2}\exp \left( \frac{m_{B_{q^\prime }}^2}{M^2}\right) \int _{m_b^2}^{s_0}ds\rho ^{\alpha _s}_{+}(s)\exp \left( -\frac{s}{M^2}\right) ,\nonumber \\ \end{aligned}$$

(25)

$$\begin{aligned}&F_{+}(q^2)+F_{-}(q^2)=-\frac{m_b^2}{f_{B_{q^\prime }}m_{B_{q^\prime }}^2}\nonumber \\&\quad \times \exp \left( \frac{m_{B_{q^\prime }}^2}{M^2}\right) \frac{m_S}{m_b} \int _{\Delta }^1du\left\{ -\frac{\phi _s(u)}{u} +\frac{\phi _\sigma (u)}{6}\frac{d}{du} \frac{1}{u}\right\} \nonumber \\&\quad \times \exp \left( -\frac{m_b^2+u\bar{u}m_S^2-\bar{u}q^2}{uM^2} \right) \nonumber \\&\quad -\frac{m_b^2}{f_{B_{q^\prime }}m_{B_{q^\prime }}^2}\exp \left( \frac{m_{B_{q^\prime }}^2}{M^2}\right) \int _{m_b^2}^{s_0}ds\rho ^{\alpha _s}_{+-}(s)\exp \left( -\frac{s}{M^2}\right) ,\nonumber \\ \end{aligned}$$

(26)

$$\begin{aligned}&F_{T}(q^2)=-\frac{m_{B_{q^\prime }}+m_S}{2f_{B_{q^\prime }}m_{B_{q^\prime }}^2}\nonumber \\&\quad \times \exp \left( \frac{m_{B_{q^\prime }}^2}{M^2}\right) \int _{\Delta }^1du\left\{ \frac{ m_b\phi (u)}{u} -\frac{ m_b^2m_S\phi _\sigma (u)}{3u^2M^2} \right\} \nonumber \\&\quad \times \exp \left( -\frac{m_b^2+u\bar{u}m_S^2-\bar{u}q^2}{uM^2} \right) -\frac{m_{B_{q^\prime }}+m_S}{2f_{B_{q^\prime }}m_{B_{q^\prime }}^2}\nonumber \\&\quad \times \exp \left( \frac{m_{B_{q^\prime }}^2}{M^2}\right) \int _{m_b^2}^{s_0}ds\rho ^{\alpha _s}_{T}(s)\exp \left( -\frac{s}{M^2}\right) , \end{aligned}$$

(27)

where $\Delta =\big [ \sqrt{(s-q^2-m_S^2)^2+4m_S^2(m_b^2-q^2)}- (s-q^2-m_S^2)\big ]/2m_S^2$, numerically $\Delta \approx \bar{\Delta }$.

3 Numerical results and discussions

The hadronic masses are taken as $m_{B^\pm }=5279.25\,\mathrm {MeV}$, $m_{B^0}=5279.55\,\mathrm {MeV}$, $m_{B_s}=5366.7\,\mathrm {MeV}$, $m_{a_0(980)}=980\,\mathrm {MeV}$, $m_{\kappa (800)}=682\,\mathrm {MeV}$, $m_{f_0(980)}=990\,\mathrm {MeV}$, $m_{a_0(1450)}=1474\,\mathrm {MeV}$, $m_{K_0^*(1430)}=1425\,\mathrm {MeV}$, $m_{f_0(1500)} = 1505\,\mathrm {MeV}$ from the Particle Data Group [34]. The threshold parameters and the decay constants of the $B_{q^\prime }$ mesons are taken from the two-point QCD sum rules $s^0_{B}=(33\pm 1)\,\mathrm {GeV}^2$, $s^0_{B_s}=(35\pm 1)\,\mathrm {GeV}^2$, $f_B=(190\pm 17)\,\mathrm {MeV}$ and $f_{B_s}=(233\pm 17)\,\mathrm {MeV}$ [35].

In the article, we take the $\overline{MS}$ mass $m_{b}(m_b)=(4.18\pm 0.03)\,\mathrm {GeV}$ from the Particle Data Group [34], and take into account the energy-scale dependence of the $\overline{MS}$ mass from the renormalization group equation,

$$\begin{aligned} m_b(\mu )&= m_b(m_b)\left[ \frac{\alpha _{s}(\mu )}{\alpha _{s}(m_b)}\right] ^{\frac{12}{23}},\nonumber \\ \alpha _s(\mu )&= \frac{1}{b_0t}\left[ 1-\frac{b_1}{b_0^2}\frac{\log t}{t} +\frac{b_1^2(\log ^2{t}-\log {t}-1)+b_0b_2}{b_0^4t^2}\right] ,\nonumber \\ \end{aligned}$$

(28)

where $t=\log \frac{\mu ^2}{\Lambda ^2}$, $b_0=\frac{33-2n_f}{12\pi }$, $b_1=\frac{153-19n_f}{24\pi ^2}$, $b_2=\frac{2857-\frac{5033}{9}n_f+\frac{325}{27}n_f^2}{128\pi ^3}$, $\Lambda =213\,\mathrm {MeV}$, $296\,\mathrm {MeV}$ and $339\,\mathrm {MeV}$ for the flavors $n_f=5$, $4$ and $3$, respectively [34]. The scale evolution behaviors of the LCDAs $\phi (u,\mu )$, $\phi _s(u,\mu )$ and $\phi _\sigma (u,\mu )$ are also determined by the renormalization group equation,

$$\begin{aligned} \bar{f}_S (\mu )&= \bar{f}_S(\mu _0)\Bigg ( \frac{\alpha _s(\mu _0)}{\alpha _s(\mu )} \Bigg )^{\frac{4}{b}},\nonumber \\ B_m(\mu )&= B_m(\mu _0) \left( \frac{\alpha _s(\mu _0)}{\alpha _s(\mu )}\right) ^{-\frac{\gamma _{m}+4}{b}}, \end{aligned}$$

(29)

where $b=(33-2n_f)/3$, and the one-loop anomalous dimensions [36, 37] is

$$\begin{aligned} \gamma _{m}= C_F \left( 1-\frac{2}{(m+1)(m+2)}+4 \sum _{j=2}^{m+1} \frac{1}{j}\right) \, . \end{aligned}$$

(30)

We take the values of the parameters in the LCDAs $\phi (u,\mu )$, $\phi _s(u,\mu )$ and $\phi _\sigma (u,\mu )$ as $\bar{f}_{a_0(980)}=(365\pm 20)\,\mathrm {MeV}$, $B_1^{a_0(980)}=-0.93 \pm 0.10$, $B_3^{a_0(980)}=0.14 \pm 0.08$, $\bar{f}_{\kappa (800)}=(340\pm 20)\,\mathrm {MeV}$, $B_1^{\kappa (800)}=-0.92 \pm 0.11$, $B_3^{\kappa (800)}=0.15\pm 0.09$, $\bar{f}_{f_0(980)}=(370\pm 20)\,\mathrm {MeV}$, $B_1^{f_0(980)}=-0.78 \pm 0.08$, $B_3^{f_0(980)}=0.02 \pm 0.07$, $\bar{f}_{a_0(1450)}=(460\pm 50)\,\mathrm {MeV}$, $B_1^{a_0(1450)}=-0.58 \pm 0.12$, $B_3^{a_0(1450)}=-0.49 \pm 0.15$, $\bar{f}_{K_0^*(1430)}=(445\pm 50)\,\mathrm {MeV}$, $B_1^{K_0^*(1430)}=-0.57 \pm 0.13$, $B_3^{K_0^*(1430)}=-0.42 \pm 0.22$, $\bar{f}_{f_0(1500)}=(490\pm 50)\,\mathrm {MeV}$, $B_1^{f_0(1500)}=-0.48 \pm 0.11$, $B_3^{f_0(1500)}=-0.37 \pm 0.20$ from the two-point QCD sum rules at the energy scale $\mu _0=1\,\mathrm {GeV}$ [33].

We evolve all the scale dependent quantities to the energy scale $\mu =\sqrt{m_B^2-m_b^2}\approx 2.4\,\mathrm {GeV}$ to calculate the transition form-factors. The constituent quarks of the scalar mesons are in essence off-shell or far from their mass-shell by the virtuality of the order $m_S^2$ as carrying the total momentum of the scalar mesons, which have a large light-cone momentum, we should take the energy scale $\mu \ge m_S$. The validity of the operator product expansion requires $0\le q^2<(m_b-m_S)^2-2(m_b-m_S)\chi$, where the $\chi$ is a typical hadronic scale of roughly 500 MeV. The available regions are $0\le q^2<11 \mathrm {GeV}^2$ for a scalar mesons $a_0(980)$, $\kappa (800)$, $f_0(980)$ and $0\le q^2<8 \mathrm {GeV}^2$ for a scalar mesons $a_0(1450)$, $K_0^*(1430)$, $f_0(1500)$.

In Figs. 2, 3, we plot the central values of the transition form-factors $F_{+}(0)$, $-F_{-}(0)$ and $F_T(0)$ with variations of the Borel parameter $M^2$. From the figures, we can see that the form-factors $F_{+}(0)$, $-F_{-}(0)$ and $F_T(0)$ for all the transitions $B\!-\!a_0(980)$, $B\!-\!\kappa (800)$, $B_s\!-\!\kappa (800)$, $B_s-f_0(980)$, $B-a_0(1450)$, $B-K_0^*(1430)$, $B_s-K_0^*(1430)$ and $B_s-f_0(1500)$ are rather stable with variations of the Borel parameter $M^2$ at the region $M^2=(8-12)\,\mathrm {GeV}^2$. So in the article, we take the Borel parameter as $M^2=(8-12)\,\mathrm {GeV}^2$.

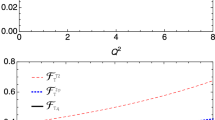
We take into account all uncertainties of the input parameters and obtain the numerical values of the transitions form-factors, which are shown explicitly in Figs. 4, 5.

Fig. 2

The central values of the form-factors $F_{+}(0)$, $F_{-}(0)$ and $F_T(0)$ with variations of the Borel parameter $M^2$, where $A$, $B$, $C$ and $D$ denote the transitions $B-a_0(980)$, $B-\kappa (800)$, $B_s-\kappa (800)$ and $B_s-f_0(980)$, respectively

Fig. 3

The central values of the form-factors $F_{+}(0)$, $F_{-}(0)$ and $F_T(0)$ with variations of the Borel parameter $M^2$, where $A$, $B$, $C$ and $D$ denote the transitions $B-a_0(1450)$, $B-K_0^*(1430)$, $B_s-K_0^*(1430)$ and $B_s-f_0(1500)$, respectively

Fig. 4

The form-factors $F_{+}(q^2)$, $F_{-}(q^2)$ and $F_T(q^2)$ with variations of the momentum transfer squared $q^2$, where $A$, $B$, $C$ and $D$ denote the transitions $B-a_0(980)$, $B-\kappa (800)$, $B_s-\kappa (800)$ and $B_s-f_0(980)$, respectively

Fig. 5

The form-factors $F_{+}(q^2)$, $F_{-}(q^2)$ and $F_T(q^2)$ with variations of the momentum transfer squared $q^2$, where $A$, $B$, $C$ and $D$ denote the transitions $B-a_0(1450)$, $B-K_0^*(1430)$, $B_s-K_0^*(1430)$ and $B_s-f_0(1500)$, respectively

The numerical values of the form-factors are fitted into the single-pole form,

$$\begin{aligned} F_{i}(q^2)&= \frac{F_{i}(0)}{1-a_{i}\frac{q^2}{m_B^2}}, \end{aligned}$$

(31)

with the MINUIT, where $m_B=5.28\,\mathrm {GeV}$, $i=+,-,T$, the values of the $F_{i}(0)$ and $a_{i}$ are shown explicitly inTables 1, 2, 3. The form-factors can be taken as basic input parameters, and study the semi-leptonic and non-leptonic $B$-decays to the scalar mesons so as to shed light on the structures of the scalar mesons or explore the CKM matrix elements.

Table 1 The parameters of the fitted transition form-factors $F_{+}(q^2)$

Table 2 The parameters of the fitted transition form-factors $F_{-}(q^2)$

Table 3 The parameters of the fitted transition form-factors $F_{T}(q^2)$

In Tables 4, 5, 6, 7, we present the $B-S$ transition form-factors from the LCSR [9–12], the three-point QCD sum rules [13–15], and also the results without perturbative ${\mathcal {O}}(\alpha _s)$ corrections in the LCSR. From the Table, we can see that the perturbative ${\mathcal {O}}(\alpha _s)$ corrections are about (15–35) % and (5–20) % for the $B-S$ form-factors with the scalar mesons bellow and above 1 GeV, respectively, we should take them into account consistently.

Table 4 The values of the $F_{+}(0)/\left( -F_{-}(0)\right)$ of the transitions $B-a_0(980)$, $B-\kappa (800)$, $B_{s}-\kappa (800)$ and ${B_{s}}-{f_{0}}(980)$ from the LCSR and QCD sum rules, where the LO denotes the leading order contributions

Table 5 The values of the $F_{+}(0)/\left( -F_{-}(0)\right)$ of the transitions $B-a_0(1450)$, $B-{K_{0}}^*(1430)$, ${B_{s}}-{K_{0}}^{*}(1430)$ and ${B_{s}}-{f_{0}}(1500)$ from the LCSR and QCD sum rules, where the LO denotes the leading order contributions

Table 6 The values of the $F_{T}(0)$ of the transitions $B-a_0(980)$, $B-\kappa (800)$, $B_s-\kappa (800)$ and $B_s-f_0(980)$ from the LCSR and QCD sum rules, where the LO denotes the leading order contributions

Table 7 The values of the $F_{T}(0)$ of the transitions $B-a_0(1450)$, $B-K_0^*(1430)$, $B_s-K_0^*(1430)$ and $B_s-f_0(1500)$ from the LCSR and QCD sum rules, where the LO denotes the leading order contributions

4 Conclusion

In the article, we assume the two scalar nonet mesons below and above 1 GeV are all $\bar{q}q$ states, in case I, the scalar mesons below 1 GeV are the ground states, in case II, the scalar mesons above 1 GeV are the ground states. We calculate the $B-S$ transition form-factors by taking into account the perturbative ${\mathcal {O}}(\alpha _s)$ corrections to the twist-2 terms using the LCSR and fit the numerical values of the form-factors into the single-pole forms. The numerical results indicate that the perturbative ${\mathcal {O}}(\alpha _s)$ corrections are about (15–35) % and (5–20) % for the $B-S$ form-factors with the scalar mesons bellow and above 1 GeV, respectively, we should take them into account consistently. The form-factors can be taken as basic input parameters, and study the semi-leptonic and non-leptonic $B$-decays to the scalar mesons so as to shed light on the structures of the scalar mesons or explore the CKM matrix elements.