Unquenched quark-model calculation of ${\varvec{X(3872)}}$ electromagnetic decays

Abstract

A recent quark-model description of $X(3872)$ as an unquenched $2\,{}^{3\!}P_1$ $c\bar{c}$ state is generalised by now including all relevant meson–meson configurations, in order to calculate the widths of the experimentally observed electromagnetic decays $X(3872)\rightarrow \gamma J/\psi$ and $X(3872)\rightarrow \gamma \psi (2S)$. Interestingly, the inclusion of additional two-meson channels, most importantly $D^\pm D^{\star \mp }$, leads to a sizeable increase of the $c\bar{c}$ probability in the total wave function, although the $D^0\bar{D}^{\star 0}$ component remains the dominant one. As for the electromagnetic decays, unquenching strongly reduces the $\gamma \psi (2S)$ decay rate; yet it even more sharply enhances the $\gamma J/\psi$ rate, resulting in a decay ratio compatible with one experimental observation but in slight disagreement with two others. Nevertheless, the results show a dramatic improvement as compared to a quenched calculation with the same confinement force and parameters. Concretely, we obtain $\Gamma \left( X(3872)\rightarrow \gamma \psi (2S)\right) =28.9$ keV and $\Gamma \left( X(3872)\rightarrow \gamma J/\psi \right) =24.7$ keV, with branching ratio $\mathcal {R}_{\gamma \psi }=1.17$.

1 Introduction

Since its discovery [1] by the Belle Collaboration in 2003, the very narrow axial-vector [2] charmonium state $X(3872)$ has become one of the favourite theoretical laboratories for meson spectroscopists, because of its remarkable closeness to the $D^0\bar{D}^{\star 0}$ (or $\bar{D}^{0} D^{\star 0}$) and $\rho ^{0}J/\psi$ thresholds, besides its seemingly too low mass for mainstream quark models. The now established [3] $J^{PC}=1^{++}$ quantum numbers seem to imply that $X(3872)$ is either the still unconfirmed [2] $\chi ^{\prime }_{c1}$ ($2\,{}^{3\!}P_1\,c\bar{c}$) meson, or an axial-vector charmonium-like state of a different kind. For a recent review, see e.g. Ref. [4].

However, in order to understand the true nature of $X(3872)$, one can ignore neither the presence of relatively nearby $1^{++}$ states in the theoretical charmonium spectrum, nor their strong coupling to the S-wave threshold $D^{0}\bar{D}^{\star 0}$. In this spirit, the properties of $X(3872)$ were recently studied in Refs. [5, 6], by modelling it as an unquenched $\chi ^{\prime }_{c1}$ state with additional meson–meson (MM) components, most importantly $D^0D^{\star 0}$.¹ In the former paper [5], a momentum-space calculation of $X(3872)$ was carried out, employing the Resonance-Spectrum Expansion (RSE), with all relevant two-meson channels included. This work showed that the hadronic decays of $X(3872)$ can thus be described quite accurately, dispensing with ad hoc tetraquark or molecular approaches. On the other hand, the latter paper [6] focused on the $X(3872)$ wave function, using instead a coordinate-space model and with only two channels, viz. $c\bar{c}$ and $D^0D^{\star 0}$. The purpose was to study whether the charm–anticharm component would remain substantial, despite the very long tail of the $D^0D^{\star 0}$ component due to the small binding of less than 0.2 MeV [2]. Indeed, a $c\bar{c}$ probability of about 7.5 % was found and—even more importantly—a corresponding wave-function component in the inner region of the same order of magnitude as that of the $D^0D^{\star 0}$ channel, thus ruling out a pure molecular scenario for $X(3872)$. Similar interpretations of $X(3872)$ were concluded in the unquenched model calculations of Refs. [7, 8].

Besides the mentioned hadronic decays, $X(3872)$ has also been observed [2] to decay in electromagnetic (EM) processes, namely to $\gamma J/\psi$ and $\gamma \psi (2S)$. Such decays are very sensitive to details of the $X(3872)$ wave function, especially in its inner region, and so may discriminate among different microscopic models. Thus, the coordinate-space method for unquenched quarkonium states employed in Ref. [6] appears to be the indicated approach for such a calculation. Now, it was shown in Refs. [9, 10] that, in a multichannel system with one almost unbound channel, more strongly bound channels should not be neglected beforehand for processes in which the wave function at short distances is important. This is of course all the more true for the $D^\pm D^{\star \mp }$ channel in the $X(3872)$ case, which is bound by only 8 MeV and so is expected to have a significant effect on the interior wave functions of the other components. Moreover, this channel contains charged mesons, which will contribute directly to EM transition amplitudes. Nevertheless, for completeness we also include all other OZI-allowed channels with combinations of pseudoscalar and/or vector charm-light as well as charm–strange mesons. As for the wave functions of the EM decay products $J/\psi$ and $\psi (2S)$, again all channels with pairs of ground-state $D$, $D^\star$, $D_s$, and $D_s^\star$ mesons will be accounted for, since they all may develop non-negligible components.

In the present paper, we shall closely follow the formalism for EM decays of unquenched, “unitarised” quarkonium systems as developed in Ref. [11]. The organisation is as follows. In Sect. 2, a multichannel Schrödinger equation for confined $q\bar{q}$ channels coupled to free MM channels is written down and solved analytically. Section 3 is devoted to the computation and display of the multicomponent wave functions of the charmonium states $X(3872)$, $J/\psi$, and $\psi (2S)$, using the generic solutions derived in Sect. 2. In Sect. 4 the procedure [11] for EM decays of quarkonium states with MM components in the wave function is reviewed. Section 5 presents the results for the EM decays, in comparison with several other published model calculations. A summary and some conclusions are given in Sect. 6.

2 Multichannel Schrödinger model

Just as in Ref. [6], we consider $X(3872)$ a coupled charm–anticharm and MM system. The transitions between the $c\bar{c}$ and MM sectors are assumed to take place via ${}^{3\!}P_0$ $q\bar{q}$ creation/annihilation at a sharp distance $a$, thus mimicking string breaking. Such a transition potential can be described in coordinate space via a spherical delta function. This choice makes the coupled-channel equations analytically solvable, provided that the confining $c\bar{c}$ potential allows solutions in terms of known functions that can be analytically continued. Thus, like in Refs. [5, 6], we take a harmonic oscillator (HO) with universal frequency $\omega$. The present generalisation beyond the model of Ref. [6] amounts to the inclusion of several MM channels instead of only one.

The coupled-channel Schrödinger equation to be solved reads

$$\begin{aligned} \left[ \begin{array}{c@{\quad }c}\hat{h}_{q\bar{q}}^{c} &{} V_{cj}\\ V_{jc}^{\dagger } &{} \hat{h}_{\mathrm{MM}}^{j} \end{array}\right] \left[ \begin{array}{c} u_{c}\\ v_{j} \end{array}\right] =E\left[ \begin{array}{c} u_{c}\\ v_{j} \end{array}\right] , \end{aligned}$$

(1)

where $\hat{h}_{q\bar{q}}$ is the quark–antiquark Hamiltonian with a confining HO potential given by

$$\begin{aligned} \hat{h}_{q\bar{q}}^{c}=m_{q}^{c}+m_{\bar{q}}^{c}+\frac{\hbar ^{2}}{2\mu _{c}}\left( -\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+\frac{l_{c}(l_{c}+1)}{r^{2}}\right) +\frac{1}{2}\mu _{c}\omega ^{2}r^{2} , \end{aligned}$$

(2)

with $\mu _c$ the reduced quark mass $m_{q}^{c}m_{\bar{q}}^{c}/(m_{q}^{c}+m_{\bar{q}}^{c})$, and $\hat{h}_{\mathrm{MM}}$ is the free MM Hamiltonian

$$\begin{aligned} \hat{h}_{\mathrm{MM}}^{j}=M_{1}^{j}+M_{2}^{j}+\frac{\hbar ^{2}}{2\mu _{j}}\left( -\frac{\mathrm{d}^{2}}{\mathrm{d}r^{2}}+\frac{L_{j}(L_{j}+1)}{r^{2}}\right) . \end{aligned}$$

(3)

Furthermore, $V_{cj}$ in Eq. (1) is the transition potential modelled through a spherical delta shell with radius $a$

$$\begin{aligned} V_{cj}=\frac{\lambda g_{cj}}{2\mu _{c}}\delta (r-a) , \end{aligned}$$

(4)

where $g_{cj}$ is the relative coupling constant of the confined $q\bar{q}$ channel $c$ to the $j$th MM channel and $\lambda$ is an overall coupling. The radial wave functions $u_{c}$ and $v_{j}$ result from the separation of the total wave function in spherical coordinates, i.e., $\psi =\frac{u(r)}{r}Y_{lm}(\theta ,\varphi )$.

We now first solve the equation analytically for $r<a$ and $r>a$ ignoring the delta shell, and then match both solutions and their derivatives at $r=a$, accounting for the delta function at this point. For the quark–antiquark components, we introduce the parameter

$$\begin{aligned} \nu _{c}=\frac{E}{\hbar \omega }-\frac{l_{c}}{2}-\frac{3}{4} \end{aligned}$$

(5)

and make the substitution $u_{c}(r)=F_{c}(r)r^{1+L_{c}}{e}^{-\frac{1}{2}\mu _{c}\omega r^{2}}$. This way we find that the solutions are of the form

$$\begin{aligned} u_{c}(r)\!=\!\left\{ \begin{array}{l} a_{c}M\left( -\nu _{c},l_{c}\!+\!\frac{3}{2},\mu _{c}\omega r^{2}\right) {e}^{-\frac{1}{2}\mu _{c}\omega r^{2}}r^{1+l_{c}},\quad r<a \\ b_{c}\,U\left( -\nu _{c},l_{c}\!+\!\frac{3}{2},\mu _{c}\omega r^{2}\right) {e}^{-\frac{1}{2}\mu _{c}\omega r^{2}}r^{1+l_{c}},\quad r>a \end{array} \right. \end{aligned}$$

(6)

where $M$ and $U$ are the Kummer and Tricomi confluent hypergeometric functions (same as the $\Phi$ and $\Psi$ functions defined in Ref. [12] and employed in Ref. [6]). Given the properties of these functions, this guarantees that $u_{c}$ is a solution to $\hat{h}_{q\bar{q}}^{c}u_{c}$ $=Eu_{c}$ for $r\ne a$, regular at the origin, and vanishing at infinity.

For the two-meson wave function, we introduce the variable $q_{j}=ip_{j}$ for each channel, with $p_{j}$ the corresponding relative momentum. Then we have

$$\begin{aligned} E=M_{1}^{j}+M_{2}^{j}-\frac{\hbar ^{2}}{2\mu _{j}}q_{j}^{2} . \end{aligned}$$

(7)

The two-meson components $v_{j}(r)$ can be written as

$$\begin{aligned} v_{j}(r)=\left\{ \begin{array}{l} A_{j}i_{L_{j}}(q_{j}r)\, r ,\quad r<a \\ B_{j}k_{L_{j}}(q_{j}r)\, r ,\quad r>a \end{array} \right. \end{aligned}$$

(8)

where $i_{l}(x)$ and $k_{l}(x)$ are the modified spherical Bessel functions of the first and third kind, respectively (cf. the functions $J_l$ and $N_l$ in Ref. [6]). The function $i_{l}$ is regular at the origin and divergent at infinity, whereas $k_{l}$ is irregular at the origin and falls off exponentially as $x\rightarrow \infty$. This solution is valid as long as the energy of the state is below all two-meson thresholds.

For convenience, we now simplify our notation, by writing $M_{c}$ for $M(-\nu _{c},l_{c}+\frac{3}{2},\mu _{c}\omega a^{2})$, $i_{j}$ for $i_{L_{j}}(q_{j}a)$, and similarly $U_c$ and $k_j$. In order to determine the coefficients $a_{c}$, $b_{c}$, $A_{j}$, and $B_{j}$, as well as the energy $E$ for a given coupling $\lambda$ or $\lambda$ for a given $E$, we first use continuity of the wave function at $r=a$, i.e.,

$$\begin{aligned} a_{c}M_{c}&= b_{c}U_{c}, \end{aligned}$$

(9)

$$\begin{aligned} A_{j}i_{j}&= B_{j}k_{j} . \end{aligned}$$

(10)

Next we integrate the Schrödinger equation (1) from $a-\epsilon$ to $a+\epsilon$, with $\epsilon$ infinitesimal. In doing so, first for the $q\bar{q}$ components, we obtain

$$\begin{aligned} -\frac{\hbar ^{2}}{2\mu _{c}}\big (u_{c}'(a^{+})-u_{c}'(a^{-})\big )+\lambda \sum _{j}\frac{g_{cj}}{2\mu _{c}a}v_{j}(a)=0 . \end{aligned}$$

(11)

This yields, by substituting the expressions for $u_{c}$ and $v_{j}$ given in Eqs. (6) and (8),

$$\begin{aligned} b_{c}U_{c}'-a_{c}M_{c}'=\lambda \frac{{e}^{\frac{1}{2}\mu _{c}\omega a^{2}}a^{-l-2}}{2\mu _{c}\omega }\sum _{j}g_{cj}A_{j}i_{j} . \end{aligned}$$

(12)

The same procedure applied to the MM channels gives the relations

$$\begin{aligned} -\frac{\hbar ^{2}}{2\mu _{j}}\big (v_{j}'(a^{+})-v_{j}'(a^{-})\big )+\lambda \sum _{c}\frac{g_{cj}}{2\mu _{c}a}u_{c}(a)=0 , \end{aligned}$$

(13)

and so using again Eqs. (6) and (8) we obtain

$$\begin{aligned} B_{j}k_{j}'-A_{j}i_{j}'=\lambda \sum _{c}\frac{g_{cj}\mu _{j}{e}^{-\frac{1}{2}\mu _{c}\omega a^{2}}{}{a}^{1+l}}{q_{j}\mu _{c}a^{2}}M_{c}a_{c} . \end{aligned}$$

(14)

We can now eliminate $b_{c}$ and $B_{j}$ from Eqs. (12) and (14) by using Eqs. (9) and (10):

$$\begin{aligned} b_{c}&= \frac{M_{c}}{U_{c}}a_{c} ,\end{aligned}$$

(15)

$$\begin{aligned} B_{j}&= \frac{i_{j}}{k_{j}}A_{j} . \end{aligned}$$

(16)

Using next Eqs. (14) and (16), we can write $A_{j}$ as a function of $a_{c}$, viz.

$$\begin{aligned} \left( \frac{k_{j}'}{k_{j}}i_{j}-i_{j}'\right) \, A_{j}=\lambda \frac{g_{j}\mu _{j}{e}^{-\frac{1}{2}m\omega a^{2}}a{}^{l-1}}{q_{j}\mu _{c}}M_{c}\, a_{c} . \end{aligned}$$

(17)

Substituting the latter result as well as Eq. (15) in Eq. (12), and defining $\alpha _{c}\equiv a_{c}M_{c}$, we find

$$\begin{aligned} \Bigg (\frac{U_{c}'}{U_{c}}-\frac{M_{c}'}{M_{c}}\Bigg )\alpha _{c}&= \lambda ^{2}\sum _{j}\frac{\mu _{j}g_{cj}}{2\mu _{c}\omega q_{j}a^{3}}\left( \frac{k{}_{j}'}{k_{j}}-\frac{i_{j}'}{i_{j}}\right) ^{-1}\nonumber \\&\quad \times \sum _{d}\frac{{e}^{\frac{1}{2}(\mu _{c}-\mu _{d})\omega a^{2}}g_{dj}}{\mu _{d}}\,\alpha _{d} . \end{aligned}$$

(18)

This set of equations is just a generalised eigensystem, with $\lambda ^{2}$ the generalised eigenvalue and $\alpha _{c}$ the generalised eigenvector, which can be written as

$$\begin{aligned} D_{c}\,\alpha _{c}=\lambda ^{2}G_{cd}\,\alpha _{d} , \end{aligned}$$

(19)

where $D$ is a diagonal matrix.

We can use the latter equation to determine the value of $\lambda$ for which there is a certain bound state with a chosen energy $E$. Alternatively, for a given $\lambda$, the energies of possible bound state can be found by employing Newton’s method to search for zeros of the determinant

$$\begin{aligned} \det (\mathrm {D}-\lambda ^{2}\mathrm {G})=0 . \end{aligned}$$

(20)

Either way, the wave-function coefficients can next be calculated from the obtained $\alpha _{c}$, using Eqs. (15–17). Finally, the scale of the coefficients can be fixed by imposing the normalisation condition

$$\begin{aligned} \sum _{c}\int _{0}^{\infty }\mathrm{d}r\, u_{c}(r)^{2}+\sum _{j}\int _{0}^{\infty }\mathrm{d}r\, v_{j}(r)^{2}=1 . \end{aligned}$$

(21)

3 ${\varvec{X(3872)}}$, ${\varvec{J/\psi }}$, and ${\varvec{\psi (2S)}}$ wave functions

Now that we have derived the general solution for the multichannel wave functions resulting from Eq. (1), we should focus on the specific wave functions of the axial-vector ($A$) charmonium system $X(3872)$ as well as the vector ($V$) states $J/\psi$ and $\psi (2S)$, since we shall consider EM decays of the former charmonium into the latter two. In order to account for all non-negligible meson-loop effects, we couple these systems to OZI-allowed channels containing pairs of the ground-state open-charm mesons $D$, $D^\star$, $D_s$ and $D_s^\star$, being either pseudoscalar ($P$) or vector ($V$). Now, $V$ states can decay into the combinations $PP$, $PV$, and $VV$, with odd orbital angular momentum $L$ because of parity conservation, whereas $A$ systems couple to channels of the $PV$ and $VV$ types, with even $L$. In Tables 1 and 2 we give the relative couplings of the different charmonia to the corresponding two-meson channels, viz. for $J/\psi$ (or $\psi (2S)$) and $X(3872)$, respectively. These couplings have been calculated employing the formalism of Ref. [13], based on overlaps in an HO basis. For economy, each listed channel in these tables really represents three channels, with e.g. $DD$ standing for $D^0D^0$, $D^\pm D^\mp$, and $D_s^+D_s^-$, all with the same coupling. Also note that in the $V$ case of $J/\psi$ and $\psi (2S)$ two $c\bar{c}$ channels must be included, viz. ${}^{3\!}S_1$ and ${}^{3\!}D_1$, giving rise to two sets of couplings.

Table 1 Squares of coupling coefficients for the vector charmonia $J/\psi$ and $\psi (2S)$. The generic notation $D$ represents $D^0$, $D^\pm$, or $D_s^\pm$ open-charm mesons

Table 2 Squares of coupling coefficients for the axial-vector charmonium $X(3872)$. Also see Table 1

Before we can compute the different wave functions, we must fix the model parameters, viz. $\omega$ (HO frequency), $m_c$ (charm-quark mass), $\lambda$ (overall coupling constant), and $a$ (string-breaking distance). Now, the former two parameters are not really free, as they have been kept fixed at the values $\omega =190$ MeV and $m_c=1562$ MeV, determined in Ref. [14], in all subsequent work. Then $\lambda$ and $a$ should be adjusted to the masses of $J/\psi$, $\psi (2S)$, and $X(3872)$, which can be done reasonably well, in spite of having only two parameters to fit three observables. Nevertheless, we believe that in the present calculation it is most important to have as accurate as possible wave functions, so that we somewhat relax the usual condition of only one $\lambda$ for all described systems. This way we are able to precisely reproduce the experimental $J/\psi$, $\psi (2S)$, and $X(3872)$ masses, with the values $\lambda _\psi =2.527$, $\lambda _X=2.176$, and $a=1.95$ GeV$^{-1}$, the coupling $\lambda _\psi$ being of course the same for $J/\psi$ and $\psi (2S)$, as we have included exactly the same MM channels for these two $V$ states. Again, ideally there should be only one $\lambda$. However, one must realise that the completeness property of the couplings $g_i$ as computed in the scheme of Ref. [13], which implies $\sum _i g_i^2=1$ for a system with any quantum numbers, is only satisfied if all decay channels are included. Well, in the latter HO-based formalism, the number of allowed channels is finite but still huge and so too large to totally account for in practical calculations. Therefore, when coupling only to the most important channels, generally those with the lowest thresholds, somewhat different values of $\lambda$ for clearly distinct systems are perfectly acceptable. Indeed, $\lambda _\psi$ and $\lambda _X$ differ by only about 15 %. Moreover, $\lambda _X=2.176$ is of the same order of magnitude as $\lambda \approx 3$ obtained in the $X(3872)$ study of Ref. [5], in which the related yet quantitatively different momentum-space RSE formalism was employed, for a similar value of the decay radius, viz. $a=2$ GeV$^{-1}$.

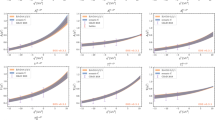
Now we are in a position to compute the three needed radial wave functions, using Eqs. (19) and (15–17). In Fig. 1 the $J/\psi$ and $\psi (2S)$ wave functions are displayed, and in Fig. 2 that of $X(3872)$.

Fig. 1

Multichannel components of $J/\psi$ (top) and $\psi (2S)$ (bottom) radial wave functions, in arbitrary units. Note that each MM curve represents the r.m.s. value of three channel wave functions, with $DD$ standing for $D^0D^0$, $D^\pm D^\mp$, or $D_s^\pm D_s^\mp$, and so forth (also see Table 1 and text). By convention and for clarity purposes, the MM curves take negative values

Fig. 2

Multichannel components of $X(3872)$ radial wave function, in arbitrary units. Also see Fig. 1 and Table 2

The first thing we observe in all three plots is a kink in the wave-function components at $r=a$, which is a direct consequence of our choosing a singular transition potential, mimicking string breaking at that precise distance. Concerning the $V$ charmonia of Fig. 1, there is a dominant $l=0$ $c\bar{c}$ wave function, which does not vanish at the origin, but also considerable $l=2$ $c\bar{c}$ and $L=1$ MM components. In the case of $X(3872)$, which has a seemingly dominant $l=1$ $c\bar{c}$ wave function, the $L=0$ $D^\pm D^{\star \mp }$ and $D^0 D^{\star 0}$ components are also very sizeable, especially the latter. As a matter of fact, the $D^0 D^{\star 0}$ channel turns out to be the most important one in terms of probability, due to its very long tail, resulting from the small binding with respect to the $X(3872)$ mass [5]. This and all other wave-function probabilities are given in Tables 3 and 4, i.e., for the $V$ charmonia and $X(3872)$, respectively.

Table 3 Percentage probabilities of $J/\psi$ and $\psi (2S)$ wave-function components, with the $c\bar{c}$ and MM numbers including $l=0,2$ and $L=1,3$ contributions, respectively. Also, $D$ stands generically for $D^0$, $D^\pm$, or $D_s^\pm$, etc., as in Fig. 1

Table 4 Percentage probabilities of $X(3872)$ wave-function components, with the MM figures including $L=0,2$ contributions. Also, the $D^\star D^\star$ value accounts for the $D^{\star 0}D^{\star 0}$, $D^{\star \pm }D^{\star \mp }$, and $D_s^{\star \pm }D_s^{\star \mp }$ summed contributions

What may look surprising in Table 3 is that $J/\psi$ has clearly larger MM components in its wave function than $\psi (2S)$. But this can be understood by observing that the decay radius $a$ is relatively close to the node in the $\psi (2S)$ $c\bar{c}$ wave function, which reduces the influence of the MM channels. As for $X(3872)$, we see in Table 4 that the $D^0 D^{\star 0}$ component is by far the largest, just like in the two-channel model study of Ref. [6]. Nevertheless, we observe a significant decrease in the latter MM channel’s probability, and a large increase in the $c\bar{c}$ probability, viz. from about 7.5 to almost 27 %, for a similar decay radius $a$. At first sight, this seems very surprising, as in the present work we include several additional MM channels. However, it must be realised that all such channels contribute to shift the $X(3872)$ bare energy level of 3929 MeV down to the physical value of 3871.69 MeV, which reduces the relative importance of the $D^0D^{\star 0}$ channel. Since it is precisely the latter wave-function component that has a very large extension in coordinate space, the reduction of its coupling will reduce its probability roughly proportionally, mostly to the benefit of the $c\bar{c}$ component.

Another way to look at the different wave-function components is by focusing on how the quenched solutions are modified by the coupling to the MM channels. For that purpose, we compute the overlaps of the unquenched $c\bar{c}$ wave functions, which are the solid curves in Figs. 1 (top, bottom) and 2, with pure HO solutions of different radial quantum number $n$, the results being given in Tables 5, 6, and 7, respectively. Note that these numbers do not concern the total wave-function overlaps, which can easily be obtained through multiplication by the $c\bar{c}$ probabilities in Tables 3 and 4. It is interesting to see that the overlaps with the lowest four radial HO states, including of course also all the $l$ states that couple, are almost sufficient to reconstruct the $c\bar{c}$ wave functions, namely to 97 % for $J/\psi$, and to even more than 99 % for $\psi (2S)$ and $X(3872)$. This might be useful for quark models with confinement mechanisms different from ours, in which sometimes HO wave functions are used to compute certain observables. In the specific case of $X(3872)$, we get an 8.82 % overlap with the $1\,{}^{3\!}P_1$ bare HO state. This is interesting, as in Ref. [18] such a component, despite being smaller in size than our result, was found to have a large influence on the EM decay widths of $X(3872)$.

Table 5 Overlap percentages of $J/\psi$ $c\bar{c}$ component with HO functions

Table 6 Overlap percentages of $\psi (2S)$ $c\bar{c}$ component with HO functions

Table 7 Overlap percentages of $X(3872)$ $c\bar{c}$ component with HO functions

To conclude this section about wave functions, we compute the r.m.s. radii of $J/\psi$, $\psi (2S)$, and $X(3872)$, obtaining 0.456, 0.930, and 6.57 fm, respectively. Notice that the latter number is somewhat smaller than the value found in Ref. [6], which is logical in view of the here reduced influence of the long $D^0 D^{\star 0}$ tail.

4 Electromagnetic transitions

In this section we review the formalism [11] for EM transitions of quarkonium systems coupled to MM channels. In order to calculate the EM decay rate of a multicomponent meson state, we couple the EM field to our coupled-channel strong-interaction Hamiltonian $\hat{H}_{q\bar{q}-\mathrm{MM}}$, obtaining a Hamiltonian of the type

$$\begin{aligned} \hat{H}=\hat{H}_{q\bar{q}-\mathrm{MM}}+\hat{H}_{{em}}+\hat{H}_{\mathrm{int}} , \end{aligned}$$

(22)

where $\hat{H}_{{em}}$ is the free EM part, in Gaussian units reading

$$\begin{aligned} \hat{H}_{{em}}=\frac{1}{8\pi }\int \mathrm{d}^{3}\mathbf {x}\, (\mathbf {E}^{2}+\mathbf {B}^{2}), \end{aligned}$$

(23)

and $\hat{H}_{\mathrm{int}}$ describes the interaction between the hadrons and the EM field. This interaction Hamiltonian can be naturally obtained from $\hat{H}_{q\bar{q}-\mathrm{MM}}$ via a minimal-coupling prescription. As we know, the hadronic coupled-channel Hamiltonian $\hat{H}_{q\bar{q}-\mathrm{MM}}$ has diagonal elements of the form

$$\begin{aligned} \hat{h}=-\frac{\hbar ^{2}}{2m_{1}}\nabla _{1}^{2}-\frac{\hbar ^{2}}{2m_{2}} \nabla _{2}^{2}+V(\mathbf {x}_{1}-\mathbf {x}_{2}) . \end{aligned}$$

(24)

The Hamiltonian for hadrons interacting with radiation is then obtained through the minimal coupling

$$\begin{aligned} -\frac{\hbar ^{2}}{2m}\nabla ^{2}\rightarrow -\frac{\hbar ^{2}}{2m}\left( \nabla -\frac{iQ}{\hbar c}\mathbf {A}\right) ^{2} . \end{aligned}$$

(25)

For the EM radiation field, we use the gauge conditions

$$\begin{aligned} \begin{array}{l} A^{0}=0, \\ \nabla \cdot \mathbf {A}=0. \end{array} \end{aligned}$$

(26)

Using Eqs. (25) and (26) and allowing for a possible anomalous magnetic moment $\mu _{i}$, we get

$$\begin{aligned} \hat{h}_{\mathrm{int}}=\sum _{i}\frac{iQ_{i}}{m_{i}c}\,\mathbf {A} (\mathbf {x}_{i})\cdot \nabla _{i}-\mu _{i}\mathbf {S}_{i}\cdot \mathbf {B} (\mathbf {x}_{i})+\frac{Q_{i}^{2}}{2m_{i}c^{2}}\mathbf {A}(\mathbf {x}_{i})^{2} \,. \end{aligned}$$

(27)

Since we are considering the EM interaction perturbatively, the term quadratic in $\mathbf {A}$ can and will be neglected. Now, for quarks and antiquarks, the magnetic moment is given by

$$\begin{aligned} \mu _{i}=\frac{Q_{i}\hbar }{m_{i}c} . \end{aligned}$$

(28)

Then the meson magnetic moment is obtained by assuming a pure $q\bar{q}$ state, resulting in the expression

$$\begin{aligned} \mu _{i}=\frac{\hbar }{2c}\left( \frac{Q_{q}}{m_{q}}+ \frac{Q_{\bar{q}}}{m_{\bar{q}}}\right) . \end{aligned}$$

(29)

Note that, apart from accounting for the mesons’ magnetic moments, the present calculation neglects their internal structure. As a consequence, to describe the EM decays of unitarised mesons, we shall only consider processes of the type

$$\begin{aligned} (Q\bar{Q})^{*}\rightarrow Q\bar{Q}+\gamma \end{aligned}$$

(30)

and

$$\begin{aligned} (M_{1}M_{2})^{*}\rightarrow M_{1}M_{2}+\gamma , \end{aligned}$$

(31)

while neglecting the ones that change the internal structure of individual mesons, viz.

$$\begin{aligned} M_{1}^{*}M_{2}^{*}\rightarrow M_{1}M_{2}+\gamma . \end{aligned}$$

(32)

As the wave function of a unitarised meson has the form

$$\begin{aligned} |\psi _{\mathrm{hadronic}}\rangle =\sum _{c}\Big |\psi _{q\bar{q}}^{c}\Big \rangle +\sum _{j}\Big |\psi _{\mathrm{MM}}^{j}\Big \rangle , \end{aligned}$$

(33)

the total matrix element for an EM transition is given by

$$\begin{aligned} \Big \langle \Psi _{f}|\hat{H}_{\mathrm{int}}|\Psi _{i}\Big \rangle&\!=\!\sum _{cc'}\Big \langle \psi _{q\bar{q}}^{c}|\hat{h}_{int}^{cc'}|\psi _{q\bar{q}}^{c'}\Big \rangle \!+\! \sum _{jj'}\Big \langle \psi _{\mathrm{MM}}^{j}|\hat{h}_{int}^{jj'}|\psi _{\mathrm{MM}}^{j'}\Big \rangle . \end{aligned}$$

(34)

The quantised EM vector potential $\mathbf {A}$ can be written in Gaussian units as [11]

$$\begin{aligned} \mathbf {A}(\mathbf {r},t)&=\sqrt{4\pi }\hbar c\sum _{\lambda lm}\int \!\frac{\mathrm{d}k}{2\pi }\frac{1}{\sqrt{2\omega _{k}}}\Bigg [ \mathbf {f}_{klm}^{(\lambda )} (\mathbf {r}){e}^{-i\omega _{k}t}a_{\lambda lm}(k)\nonumber \\&\quad +\mathbf {f}_{klm}^{(\lambda )}(\mathbf {r})^{*}{e}^{-i\omega _{k}t} a_{\lambda lm}^{\dagger }(k)\Bigg ]. \end{aligned}$$

(35)

where the index $\lambda \in \{e,m\}$ indicates whether the component is an electric multipole or a magnetic multipole. For instance, the components with $\lambda =e$ and $l=2$ correspond to electric quadrupole (E2) radiation, while those with $\lambda =m$ and $l=1$ stand for magnetic dipole (M1) radiation. Furthermore, $a_{\lambda lm}(k)$ and $a_{\lambda lm}^{\dagger }(k)$ are photon annihilation and creation operators obeying the commutation relations

$$\begin{aligned} \Bigg [a_{\lambda lm}(k),a_{\lambda 'l'm'}^{\dagger }(k')\Bigg ]=2\pi \delta (k'-k) \delta _{\lambda '\lambda }\delta _{l'l}\delta _{m'm} . \end{aligned}$$

(36)

The vector fields $\mathbf {f}_{kJM}^{(\lambda )}(\mathbf {r})$ are given by [11]

$$\begin{aligned} \mathbf {f}_{klm}^{(m)}(\mathbf {r})=2kj_{l}(kr)\sum _{q}C_{lm-q1q}^{lm}Y_{lm-q}(\theta ,\varphi )\hat{\mathbf {e}}_{q} \end{aligned}$$

(37)

and

$$\begin{aligned} \mathbf {f}_{klm}^{(e)}(\mathbf {r})=&2k\sum _{q}\Bigg [j_{l-1}(kr)\sqrt{\frac{l+1}{2l+1}}C_{l-1,m-q,1q}^{l-1,m}Y_{l-1,m-q}(\hat{\mathbf {r}})\nonumber \\&-\!j_{l+1}(kr)\sqrt{\frac{l}{2l+1}}C_{l\!+\!1,m-q,1q}^{l+1,m}Y_{l+1,m-q}(\hat{\mathbf {r}})\Bigg ]\hat{\mathbf {e}}_{q} , \end{aligned}$$

(38)

with

$$\begin{aligned} \hat{\mathbf {e}}_{\pm 1}&= \mp \frac{\hat{\mathbf {e}}_{x}\pm i\hat{\mathbf {e}}_{y}}{\sqrt{2}} , \\ \hat{\mathbf {e}}_{0}&= \hat{\mathbf {e}}_{z} . \end{aligned}$$

They have the properties [11]

$$\begin{aligned}&\nabla \times \mathbf {f}_{klm}^{(e)}=-ik\mathbf {f}_{klm}^{(m)},\end{aligned}$$

(39)

$$\begin{aligned}&\nabla \times \mathbf {f}_{klm}^{(m)}=ik\mathbf {f}_{klm}^{(e)},\end{aligned}$$

(40)

$$\begin{aligned}&\nabla .\mathbf {f}_{klm}^{(\lambda )}=0,\end{aligned}$$

(41)

$$\begin{aligned}&\int \mathrm{d}^{3}\mathbf {x}\,\mathbf {f}_{klm}^{(\lambda )}(\mathbf {x})\cdot \mathbf {f}_{k'l'm'}^{(\lambda ')}=2\pi \delta (k'-k)\delta _{ll'} \delta _{mm'}\delta _{\lambda \lambda '} . \end{aligned}$$

(42)

Now, we have an initial state $|\Psi _{i}\rangle =|nJM\rangle \otimes |0\rangle$, where $|0\rangle$ denotes the photon vacuum, and a final state $|\Psi _{f}\rangle =|n'J'M'\rangle \otimes |\lambda klm\rangle$, where

$$\begin{aligned} |\lambda klm\rangle =a_{\lambda klm}^{\dagger }|0\rangle . \end{aligned}$$

(43)

Substituting next Eqs. (35), (37), and (38) into the matrix element

$$\begin{aligned} \mathcal {M}_{if}=\Big \langle \Psi _{f}|\hat{H}_{\mathrm{int}}|\Psi _{i}\Big \rangle , \end{aligned}$$

(44)

we finally obtain, after a laborious yet straightforward calculation, the electric and magnetic decay matrix elements [11]. The results are given in Appendix A.

5 Results and comparison of EM decay rates

Now we can present the results for our model calculation of the $X(3872)$ EM decays. First, though, we show in Table 8 the up-to-date experimental status of such decays, which is clearly poor. First of all, only lower bounds are reported for the $\gamma J/\psi$ and $\gamma \psi (2S)$ rates. On the other hand, for the very small total $X(3872)$ width, merely an upper bound of 1.2 MeV is listed [2]. This is understandable, as small enough bin sizes to pin down the width more precisely are not possible with present-day statistics. But, as a consequence, the absolute magnitudes of the two observed EM decays are largely unknown. Only their ratio

$$\begin{aligned} \mathcal {R}_{\gamma \psi }\equiv \frac{\Gamma \left( X(3872)\rightarrow \gamma \psi (2S)\right) }{\Gamma \left( X(3872)\rightarrow \gamma J/\psi \right) } \end{aligned}$$

(45)

has been determined by two experiments, though still with large errors (Table 8). Coming now to our model predictions, we first observe that a process of the type $^{3\!}P_1\rightarrow \gamma \,{}^{3\!}S_1/{}^{3\!}D_1$ is dominated by an electric dipole (E1) transition, besides a smaller magnetic quadrupole (M2) contribution. Using the expressions in Appendix A, we then obtain the results presented in Table 9.

Table 8 Experimental results for EM decays of $X(3872)$

Table 9 Predictions (in keV) of E1 and M2 EM decays widths

As expected, the M2 widths are much smaller than the E1 ones, since higher multipoles are suppressed by powers of photon momentum divided by (charm) quark mass [32]. Such a behaviour is roughly confirmed by our numbers, as the photon in the process with $J/\psi$ in the final state has about four times as much momentum as in the decay to $\psi (2S)$ [2]. Clearly, experimental statistics is insufficient so far to do an angular analysis needed [33] for disentangling the E1 and M2 contributions in the $X(3872)$ EM data. Therefore, in order to compare our prediction for the EM branching-rate ratio defined in Eq. (45) with the experimental values given in Table 8, we simply sum the E1 and M2 contributions, obtaining $\mathcal {R}_{\gamma \psi }=1.17$. This number is compatible with the Belle [16] upper bound of 2.1, but somewhat too small as compared to the BaBar [15] and LHCb [17] measurements. However, the experimental values are only marginally in agreement with one another and the uncertainties are still very large. If we take our absolute EM-width predictions at face value, in particular the result 28.9 keV for $\Gamma \left( X(3872)\rightarrow \gamma \psi (2S)\right)$, the experimental lower bound $\mathcal {B}_{\gamma \psi (2S)}>0.030$ [15] implies $\Gamma \left( X(3872)\right)$ $<1$ MeV, slightly lower than the PDG [2] upper limit of 1.2 MeV. Nevertheless, the $X(3872)$ total width is probably even smaller than that, considering the $S$-matrix pole trajectories of the $X(3872)$ resonance near the $D^0D^{\star 0}$ threshold in the multichannel RSE calculation of Ref. [5].

Next, in Table 10 we compare the present EM results to those of a number of other model calculations (also see Ref. [30]). Clearly, our values are somewhere in the middle of the ballpark of often disparate numbers. Generally, one may conclude that the experimental EM rate ratio seems to favour models based on a $2\,{}^{3\!}P_1$ $c\bar{c}$ assignment for $X(3872)$, with or without other components.

Table 10 Comparison of model predictions for the EM decays of $X(3872)$. mol molecule, unq unquenched $c\bar{c}$, EFT effective field theory, @ present work. Models assume $1^{++}$ quantum numbers, unless otherwise specified

Finally, we have a look at the importance of unquenching in our model. To that end, we compute the EM predictions from bare HO $c\bar{c}$ wave functions only, with unchanged parameters except for the overall couplings to MM channels, which are set to zero. Note that this results in bare $J/\psi$, $\psi (2S)$, and $X(3872)$ masses that are roughly 300, 100, and 100 MeV larger than the physical ones, respectively. Having this proviso in mind, we obtain for the total EM widths $\Gamma _{\mathrm{quenched}} \left( X(3872)\rightarrow \gamma J/\psi \right) =0.61$ keV and $\Gamma _{\mathrm{quenched}}\left( X(3872)\rightarrow \gamma \psi (2S)\right) =159$ keV. Here we should remark that the former width, which corresponds to an $2P\rightarrow 1S$ EM transition, is sometimes reported [30, 31] to vanish identically for three-dimensional HO wave functions. However, this is only true in the long-wave-length (alias dipole) approximation, used in e.g. Ref. [31], and not in the more general formalism of Ref. [11] employed here. The latter article showed that the dipole approximation is rather poor for several E1 transitions in charmonium. Nevertheless, the very small quenched EM width we find for $X(3872)\rightarrow \gamma J/\psi$ shows that in this particular situation the approximation looks reasonable. Anyhow, comparing to the unquenched total (E1 + M2) widths in Table 9, we see a rather dramatic importance of unquenching.

Concluding our study of multichannel effects, we calculate the separate contributions from the $c\bar{c}$ and the MM channels. Note that this is done in the full model and so using the wave functions plotted in Figs. 1 and 2. The total exclusive $c\bar{c}$ and MM results are then obtained by setting the wave functions of the MM and $c\bar{c}$ components to zero by hand, respectively. Thus, we get $\Gamma ^{c\bar{c}}_{\gamma J/\psi }=15.3$ keV, $\Gamma ^{MM}_{\gamma J/\psi }=1.12$ keV, $\Gamma ^{c\bar{c}}_{\gamma \psi (2S)}=28.0$ keV and $\Gamma ^{MM}_{\gamma \psi (2S)}=0.01$ keV. These results reveal constructive interference effects, especially in the $J/\psi$ case, as one cannot just sum the $c\bar{c}$ and MM numbers to obtain the widths in Table 9.

6 Summary and conclusions

This paper is the third part of a triptych aimed at understanding the microscopic dynamics of the enigmatic charmonium state $X(3872)$. The first article [5] was devoted to its hadronic decays, including the OZI-forbidden ones, arriving at a good description of the available data. The second paper [6] focused on the importance of $X(3872)$’s $c\bar{c}$ component, concluding that a purely molecular assignment is ruled out. In our present work, we have generalised the $r$-space method employed in the latter paper so as to include all virtual open-charm MM channels that may contribute significantly to the $X(3872)$ wave function, as well as to those of the vector charmonia $J/\psi$ and $\psi (2S)$. These wave functions have then been used to compute the widths of the experimentally observed EM decay processes $X(3872)\rightarrow \gamma J/\psi$ and $X(3872)\rightarrow \gamma \psi (2S)$, employing the formalism developed and applied to charmonium and bottomonium in Ref. [11].

In the first place, and concerning the thus obtained wave functions, it is quite remarkable that the inclusion of several additional MM channels to describe $X(3872)$, most notably the $D^\pm D^{\star \mp }$ channel bound by only about 8 MeV, gives rise to an increase of the $c\bar{c}$ probability from 7.48 % [6] to 26.76 %. Accordingly, the $c\bar{c}$ wave-function component becomes clearly the dominant one, except at very small and very large distances. However surprising at first sight, this effect can be explained by the reduced influence of the narrowly bound $D^0D^{\star 0}$ channel, which has an extremely long tail and so takes up most of the total probability. This is also confirmed by the reduction of the $X(3872)$ r.m.s. radius from 7.82 fm in Ref. [6] to 6.57 fm here. As for the $J/\psi$ and $\psi (2S)$ wave functions, we find significant ${}^{3\!}D_1$ $c\bar{c}$ and P-wave MM components, the former most prominently for $\psi (2S)$ and the latter especially in the $J/\psi$ case. The closeness of the $\psi (2S)$ wave-function node to the decay radius $r$ offers an explanation for the relatively reduced importance of MM channels for the first radially excited vector charmonium state.

Coming now to the EM transitions of $X(3872)$, we obtain total widths of 28.9 keV and 24.7 keV for the decays to $\gamma \psi (2S)$ and $\gamma J/\psi$, respectively, with rate ratio $\mathcal {R}_{\gamma \psi }=1.17$. While there are no data for the absolute magnitudes of the EM widths, the latter ratio can be compared to three experimental values. Thus, our prediction of 1.17 is fully compatible with the upper bound of 2.1 observed by the Belle Collaboration [16], but a little bit too low for the numbers $3.4\pm 1.4$ and $2.46\pm 0.64\pm 0.29$ reported by BaBar [15] and LHCb [17], respectively. Although the experimental error bars are still quite large and the three observations so far are nonetheless only in marginal agreement with one another, additional mechanisms—not considered here—might remove the slight discrepancy. One possibility is the inclusion of photonic decays of individual mesons in the MM channels, that is, observed [2] processes of the type $D^{\star +}\rightarrow D^+\gamma$, $D^{\star 0}\rightarrow D^0\gamma$, and $D_s^{\star +}\rightarrow D_s^+\gamma$. Another source may be relativity, as relativistic effects are capable of shifting the nodes in the $X(3872)$ and $\psi (2S)$ $c\bar{c}$ wave-function components [11], thus affecting the overlap integrals. While these issues are certainly worthwhile to be studied in future work, the most important contribution to an even better understanding of $X(3872)$ will be improved measurements, with higher statistics and smaller bin sizes ($<$1 MeV if ever possible), in order to pin down the absolute magnitudes of the EM decay widths, as well as the total width.

Appendix: EM transition matrix elements

The multipolar electric transition matrix elements are given by [11]

$$\begin{aligned}&\mathcal {M}_{if}^{e}\nonumber \\&\quad \!\!= i\sqrt{\hbar \omega }(\!-\!1)^{m\!+\!L'}C_{M\, m\, M'}^{J\, l\, J'}\sqrt{(2J\!+\!1)(2L\!+\!1)(2l\!+\!1)(2L'\!+\!1)}\nonumber \\&\qquad \times \left( \begin{array}{c@{\quad }c@{\quad }c}L' &{} l &{} L\\ 0 &{} 0 &{} 0 \end{array}\right) \Bigg [ Q(-1)^{J+L'+S'+1}\frac{\delta _{SS'}}{\sqrt{l(l+1)}}\nonumber \\&\qquad \times \left\{ \begin{array}{c@{\quad }c@{\quad }c} J &{} l &{} J'\\ L' &{} S' &{} L \end{array}\right\} (R_{1}+R_{2})+(-1)^{1+S_{1}+S_{2}}\nonumber \\&\qquad \times \sqrt{(2l+1)(2S+1)(2S'+1)}\left\{ \begin{array}{c@{\quad }c@{\quad }c} L &{} l &{} J\\ S &{} 1 &{} S'\\ J &{} L &{} J' \end{array}\right\} \nonumber \\&\qquad \!\times \!\Bigg [(\!-\!1)^{S}2\mu _{1}\frac{\hbar \omega }{c}\sqrt{S_{1}(S_{1}\!+\!1)(2S_{1}\!+\!1)} \left\{ \begin{array}{c@{\quad }c@{\quad }c} S &{} 1 &{} S'\\ S_{1} &{} S_{2} &{} S_{1} \end{array}\right\} \nonumber \\&\qquad \times R_{0,l}^{(1)}- (-1)^{l+S'}2\mu _{2}\frac{\hbar \omega }{c}\sqrt{S_{2}(S_{2}+1)(2S_{2}+1)}\nonumber \\&\qquad \times \left\{ \begin{array}{c@{\quad }c@{\quad }c} S &{} 1 &{} S'\\ S_{2} &{} S_{1} &{} S_{2} \end{array}\right\} R_{0,l}^{(2)}\Bigg ]\Bigg ] , \end{aligned}$$

(46)

with the radial integrals

$$\begin{aligned} R_{0,l}^{(i)}&= \int _{0}^{\infty }\mathrm{d}r\, u_{f}(r)j_{l}\left( \frac{\mu }{m_{i}}kr\right) u_{i}(r) ,\end{aligned}$$

(47)

$$\begin{aligned} R_{1}&= \int _{0}^{\infty }\mathrm{d}r\, u_{f}(r)\left[ 1+r\frac{\partial }{\partial r}\right] \left[ j_{l}\left( \frac{\mu }{m_{1}}kr\right) \right. \nonumber \\&\left. -(-1)^{l}j_{l}\left( \frac{\mu }{m_{2}}kr\right) \right] u_{i}(r),\end{aligned}$$

(48)

$$\begin{aligned} R_{2}&= \int _{0}^{\infty }\mathrm{d}r\, u_{f}(r)\left[ \frac{\mu }{m_{1}}\frac{\hbar \omega }{m_{1}c^{2}}\,j_{l}\left( \frac{\mu }{m_{1}}kr\right) \right. \nonumber \\&\left. -(-1)^{l}\frac{\mu }{m_{2}}\frac{\hbar \omega }{m_{2}c^{2}}\,j_{l}\left( \frac{\mu }{m_{2}}kr\right) \right] \,r\frac{\partial }{\partial r}u_{i}(r) . \end{aligned}$$

(49)

The multipolar magnetic transition matrix elements are [11]

$$\begin{aligned} \mathcal {M}_{if}^{m}&= i\sqrt{\hbar \omega }(-1)^{m+L'+1} C_{M\, m\, M'}^{J\, l\, J'}\sqrt{(2J+1)(2L'+1)}\\&\quad \times \left( \begin{array}{c@{\quad }c@{\quad }c} L' &{} l &{} L\\ 0 &{} 0 &{} 0 \end{array}\right) \\&\quad \times \left[ Q\delta _{SS'}(-1)^{J+L'+S'}(2l+1)\left\{ \begin{array}{c@{\quad }c@{\quad }c} L' &{} L &{} l\\ J &{} J' &{} S \end{array}\right\} \right. \\&\quad \times \left[ \sqrt{(2L+3)(L+1)}\left( \begin{array}{c@{\quad }c@{\quad }c} L' &{} l &{} L+1\\ 0 &{} 0 &{} 0 \end{array}\right) \right. \\&\quad \times \left\{ \begin{array}{c@{\quad }c@{\quad }c} L' &{} L &{} l\\ 1 &{} l &{} L+1 \end{array}\right\} R_{3,-L}\\&\quad -\sqrt{(2L-1)L}\left( \begin{array}{c@{\quad }c@{\quad }c} L' &{} l &{} L-1\\ 0 &{} 0 &{} 0 \end{array}\right) \\&\quad \left. \times \left\{ \begin{array}{c@{\quad }c@{\quad }c} L' &{} L &{} l\\ 1 &{} l &{} L-1 \end{array}\right\} R_{3,L+1}\right] \\&\quad \times 2(-1)^{S_{1}+S_{2}+1}\sqrt{(2L+1)(2S+1)(2S'+1)}\\&\quad \times \left[ \mu _{1}\frac{\hbar \omega }{c}(-1)^{S}\sqrt{S_{1}(S_{1}+1)(2S_{1}+1)}\right. \\&\quad \times \left\{ \begin{array}{c@{\quad }c@{\quad }c} S &{} 1 &{} S'\\ S_{1} &{} S_{2} &{} S_{1} \end{array}\right\} \\&\quad \times \left[ \sqrt{l(2l+3)}\left\{ \begin{array}{c@{\quad }c@{\quad }c} L &{} l+1 &{} L'\\ S &{} 1 &{} S'\\ J &{} l &{} J' \end{array}\right\} \right. \\&\quad \times \left( \begin{array}{c@{\quad }c@{\quad }c} L' &{} l+1 &{} L\\ 0 &{} 0 &{} 0 \end{array}\right) R_{0,l+1}^{(1)}\\&\quad - \sqrt{(l+1)(2l-1)}\left\{ \begin{array}{c@{\quad }c@{\quad }c} L &{} l-1 &{} L'\\ S &{} 1 &{} S'\\ J &{} l &{} J' \end{array} \right\} \\&\quad \left. \times \left( \begin{array}{c@{\quad }c@{\quad }c} L' &{} l-1 &{} L\\ 0 &{} 0 &{} 0 \end{array}\right) R_{0,l-1}^{(1)} \right] \\&\quad +(-1)^{l+S'}\mu _{2}\frac{\hbar \omega }{c}\sqrt{S_{2}(S_{2}+1)(2S_{2}+1)}\\&\quad \times \left\{ \begin{array}{c@{\quad }c@{\quad }c} S &{} 1 &{} S'\\ S_{2} &{} S_{1} &{} S_{2} \end{array}\right\} \\&\quad \times \left[ \sqrt{l(2l+3)}\left\{ \begin{array}{c@{\quad }c@{\quad }c} L &{} l+1 &{} L'\\ S &{} 1 &{} S'\\ J &{} l &{} J' \end{array}\right\} \right. \\&\quad \times \left( \begin{array}{c@{\quad }c@{\quad }c} L' &{} l+1 &{} L\\ 0 &{} 0 &{} 0 \end{array}\right) R_{0,l+1}^{(2)}\\&\quad - \sqrt{(l+1)(2l-1)}\left\{ \begin{array}{c@{\quad }c@{\quad }c} L &{} l-1 &{} L'\\ S &{} 1 &{} S'\\ J &{} l &{} J' \end{array}\right\} \\&\quad \left. \left. \left. \times \left( \begin{array}{c@{\quad }c@{\quad }c} L' &{} l-1 &{} L\\ 0 &{} 0 &{} 0 \end{array}\right) R_{0,l-1}^{(2)}\right] \right] \right] , \end{aligned}$$

with

$$\begin{aligned} R_{3L}&= \int _{0}^{\infty }\mathrm{d}r\, u_{f}(r)\left[ \frac{\hbar }{m_{1}c}\, j_{l}\left( \frac{\mu }{m_{1}}kr\right) \right. \nonumber \\&\left. -(-1)^{l}\frac{\hbar }{m_{2}c}\, j_{l}\left( \frac{\mu }{m_{2}}kr\right) \right] \,\left[ \frac{\partial }{\partial r}+\frac{L}{r}\right] \,u_{i}(r) . \end{aligned}$$

Accounting for the recoil of the final-state meson, the photon momentum $k$ is given by

$$\begin{aligned} k=\frac{M_{i}^{2}-M_{f}^{2}}{2M_{i}}c . \end{aligned}$$

(50)

The decay width is then given by the Fermi golden rule

$$\begin{aligned} \Gamma ^{(\lambda )}=\frac{2\pi }{\hbar }\Big |\mathcal {M}_{if}^{\lambda }\Big |^{2}\rho _{f} , \end{aligned}$$

(51)

where $\rho _{f}$ is the density of final states $\rho _{f}=1/2\pi \hbar c$.