1 Introduction

The question of determining the model that best describes the universe is the ultimate goal of cosmology. The energy-momentum content of the present universe seems to be a perfect fluid mainly consisting of a dark sector (possibly consisting of a dark energy and a dark matter component), baryonic matter, and radiation [1–3]. In the standard model of cosmology (namely, \(\Lambda \)CDM) dark matter [4] and baryonic matter are considered to be dust, dark energy [5–7] is taken to be the Einstein cosmological constant, and radiation is described by the usual energy-momentum term for radiation. Although the standard model seems to be compatible with observations yet it has some problems. The magnitudes of potential theoretical contributions to the cosmological constant (CC) are extremely much higher than the value of CC deduced from the energy density of the universe [8–12]. There are many attempts to solve this problem, the CC problem. Nevertheless none is wholly satisfactory. The best option seems to employ a symmetry such as a metric reversal symmetry [13–18] to cancel CC and then attribute the dark energy to something else, e.g. to modified gravity [19], or to some scalar field such as quintessence [20–23]. The cold dark matter (i.e. dust-like dark matter with no or negligible interaction with itself and with baryonic matter and photons) scenario of \(\Lambda \)CDM as well suffers from some problems such as rotation curves of spiral-like galaxies, i.e. the cuspy halo problem, and the missing satellite galaxies problem [24, 25]. There are many alternatives to the cold dark matter (CDM) scenario, including warm dark matter [26, 27], Bose–Einstein condensate dark matter [28–32], and scalar field dark matter [33–36].

The above considerations essentially hold for the time from the radiation dominated era till the present era. The standard paradigm for the era before the radiation dominated era is an inflationary era (which serves to solve the problems of the standard cosmology such as horizon, flatness, absence of monopoles problems) [37, 38]. Usually the inflationary era and the epoch after this era are studied separately. This is not only due to the need to concentrate on each of these and to try to understand each epoch better before a possible unification. In fact the most serious problem in the direction of the unificationFootnote 1 of the whole cosmic history is the difficulty of merging these two epochs because of the form of the dependence of the energy density of dust and radiation on the scale factor (i.e. on redshift). In \(\Lambda \)CDM the energy density of radiation dominates over that of the inflaton if one goes back to sufficiently large redshifts. This is due to the fact that the energy density of the inflaton is essentially constant during the inflationary era, while the energy density of radiation scales like \(\frac{1}{a^4}\) where \(a\) is the scale factor. In other words, to have a true unification, the creation of radiation and matter after the inflationary era must be taken into account in the scale factor without destroying the standard cosmology before and after the inflation, and this is not an easy task. The models in literature that unify all eras of cosmological evolution in a single model [39–42] are not wholly realistic since they do not include baryonic matter, although they are able to produce eras of cosmological evolution with correct equations of state in the corresponding eras, and some have a graceful exit from the inflationary era. The matter in these models must be identified with dark matter since the energy densities of these models do not contain energy components that scale proportional to \(\frac{1}{a^3}\) for all times (or at least for a sufficiently long time). The models in [39–41] use the energy densities expressed in terms of simple functions of Hubble parameter and/or scale parameter as the starting point rather than starting from the scale factor. Although one may, in principle, determine the scale factor from this information, the form of scale factor may be rather complicated in some cases. On the other hand a relatively simple scale factor may result in a rather complicated and unmanageable functional form for the energy density when expressed in terms of the scale factor or the Hubble parameter. Therefore, in some cases it may be more suitable to consider a specific ansatz for the scale factor such as in this study and in [42]. The same approach is adopted in this study. Moreover, the present study introduces a general prescription to include dust and radiation into unification.

In this study, first, in Sect. 2, we introduce a scheme to unify the cosmological evolution before and after the radiation dominated era. Then we give a concrete realization of this scheme in Sect. 3. In Sect. 4 we discuss the observational compatibility of this scheme in the context of the model introduced in Sect. 3. Finally we conclude in Sect. 5. The scale factor in this model is a sum of two terms. The first term is a pure dark energy contribution. The second term is responsible for the baryonic matter and radiation terms and additional terms that may be mainly identified with dark matter. There is also an additional term due to coupling between these terms, and this term gives another contribution to the dark energy and dark matter. Some of the ideas employed here have been already studied in literature. In this study we do not make a sharp distinction between dark energy and dark matter, because the dark energy and dark matter terms are coupled and the equation of state (EoS) of some terms, e.g. EoS of the coupling term between dark matter and dark energy terms, evolves with time. The superficiality of a distinction between dark energy and dark matter is considered in many studies in the literature, either explicitly or implicitly [43–47]. This option is quite possible since dark energy and dark matter are not observed directly. What we see observationally is a missing element in the energy-momentum tensor of the Einstein equations, other than baryonic matter and radiation, and this missing quantity may be described by two components: dark energy and dark matter. It is, in principle, equally possible that this quantity is composed of a single component, say, dark fluid. In [42] we had introduced a universe composed of a dark fluid (which may be written in terms of two scalar fields). In fact the scale factor in that study is essentially \(a_1(t)\) in Eq. (2) of this paper. The present study may be considered somewhat as an extension of [42] where baryonic matter and radiation are included. However, there are important differences as well. The main aim of this study is to introduce a scheme to merge the cosmological evolution of the time before and after the production of radiation into a single scale factor with the baryonic matter and the usual radiation terms included. The modified form of \(a_1(t)\) in [42] only serves as a realization of this scheme. Furthermore we do not discuss the scalar field identification of the energy density due the part of the scale factor similar to \(a_1(t)\) of [42] (although it can easily be done), and we do not consider the cosmological perturbations of these quantities, and the inflationary era in this study because these points would cause divergence of the main goal of the paper and would increase the volume of this study drastically. We leave these points to future studies.

2 Outline of the model

Consider the Robertson–Walker metric

$$\begin{aligned} \mathrm{d}s^2=g_{\mu \nu }\mathrm{d}x^\mu \,\mathrm{d}x^\nu =-\mathrm{d}t^2\,+\,a^2(t)\tilde{g}_{ij}\mathrm{d}x^i\mathrm{d}x^j .\end{aligned}$$
(1)

We take the 3-dimensional space be flat, i.e. \(\tilde{g}_{ij}=\delta _{ij}\) for the sake of simplicity, which is an assumption consistent with cosmological observations [48, 49]. We let the form of the scale factor be

$$\begin{aligned} a(t)&= c_0\left( a_1(t)\,-\,a_2(t)\right) \nonumber \\ c_0&= \frac{1}{A_1-A_2},\quad A_1=a_1(t_0),\quad A_2=a_2(t_0) \end{aligned}$$
(2)

where \(t_0\) denotes the present time. We will see that \(a_1(t)\) is the part of the scale factor responsible for dark energy and dark matter, and \(a_2(t)\) is the one mainly responsible for dust and radiation and additional contribution to dark matter-energy, and we shall see later that a mixing between the sectors due to \(a_1\) and \(a_2\) act as an additional source of dark energy. We assume that \(a_1(t)\) and \(a_2(t)\) are chosen in such a way that \(a(t)\,>\,0\) for all \(t\). In general one may identify the dust by a mixture of baryonic matter and dust-like dark matter. The best fit values that we could find by trial and error for the specific toy model considered in this study for implementation of the present scheme seem to prefer the case where the dust term is wholly or almost wholly due to baryonic matter.

We first focus on the \(a_2(t)\) term and specify it as

$$\begin{aligned} a_2(t)=x(t)\,a(t) \end{aligned}$$
(3)

where \(x(t)\) is some function that its form will be specified later. Equations (2) and (3) may be used to relate \(a(t)\) and \(a_1(t)\), \(a_2(t)\) in a more applicable way, and to derive the corresponding Hubble parameter. We observe that

$$\begin{aligned} a_2&= ax=c_0(a_1-a_2)x~~~\Rightarrow ~~ a_2=\frac{c_0x}{1+c_0x}a_1,\nonumber \\&a=\frac{c_0}{1+c_0x}a_1=\frac{1}{x}a_2 .\end{aligned}$$
(4)

In a similar way the Hubble parameter is found to be

$$\begin{aligned} \frac{\dot{a}_2}{a}=\frac{\dot{a}}{a}\,+\,\dot{x}~~~\Rightarrow ~~~ H=\frac{\dot{a}}{a}= \frac{\dot{a}_{1n}}{a_{1n}} -\frac{c_0\dot{x}}{1+c_0x} \end{aligned}$$
(5)

where we have used

$$\begin{aligned} \frac{\dot{a}_1}{a}&= \left( \frac{1+c_0x}{c_0}\right) \frac{\dot{a}_1}{a_1}~,~~ \frac{\dot{a}_{1}}{a_{1}}= \frac{\dot{a}_{1n}}{a_{1n}} \nonumber \\&a_1=A_1\,a_{1n}~,~~a_{1n}(t_0)=1 .\end{aligned}$$
(6)

Note that \(a(t_0)=1\) by convention.

We let

$$\begin{aligned}&\!\!\!x(t)=A_2\frac{1}{c_1-c_2}x_3(t)\left( c_1x_1(t)-c_2x_2(t)\right) , \end{aligned}$$
(7)
$$\begin{aligned}&\!\!\!x_1(t)=\exp {\int _{t_0}^t\tilde{H}_2^{(1)}dt}~,~~x_2(t)= \exp {\int _{t_0}^t\tilde{H}_2^{(2)}dt} , \end{aligned}$$
(8)
$$\begin{aligned}&\!\!\!x_3(t)= \exp {\int _{t_0}^t\tilde{H}_2^{(3)}dt} \end{aligned}$$
(9)

where \(c_1\), \(c_2\) are some constant coefficients, and

$$\begin{aligned}&\!\!\!\tilde{H}_2^{(1)} =\alpha _{o1}\left[ -\frac{\alpha _b}{a^{\frac{3}{2}}}- \frac{\alpha _r}{a^2}+\frac{\alpha _x}{a^3}\right] \,,\nonumber \\&\!\!\!\tilde{H}_2^{(2)} =\alpha _{o2}\left[ \frac{\alpha _b}{a^{\frac{3}{2}}}+ \frac{\alpha _r}{a^2}-\frac{\alpha _K}{a}\right] \,,\nonumber \\&\!\!\! \tilde{H}_2^{(3)} =\alpha _c\left( \frac{1}{a^3}-\frac{1}{a}\right) \end{aligned}$$
(10)

where \(\alpha _{o1}\), \(\alpha _{o2}\), \(\alpha _b\), \(\alpha _r\), \(\alpha _x\), \(\alpha _K\) are some other constant coefficients. In fact, in Eq. (7) we could take the simpler form where \(\alpha _c=0\), \(\alpha _{o1}=\alpha _{o2}=1\), \(c_1=1\), \(c_2=0\). This would be enough as long as we are concerned only with merging of the eras before and after the radiation domination, and the resulting model would be compatible with Union2 data set at an order of magnitude level. The more involved form in Eq. (7) is used to make the model phenomenologically more viable. This point will be discussed when we discuss the phenomenological viability of the model in Sect. 4. One may determine \(\dot{x}\) in Eq. (5) by using Eq. (7),

$$\begin{aligned}&\!\!\!\dot{x}(t) =A_2\frac{1}{c_1-c_2}x_3\nonumber \\&\quad \!\!\! \times \left[ -B(t)\left( \frac{\alpha _b}{a^\frac{3}{2}}+ \frac{\alpha _r}{a^2}\right) \,+\,S(t)\frac{\alpha _x}{a^3}\,+\,K(t) \frac{\alpha _K}{a}\right] \end{aligned}$$
(11)

where

$$\begin{aligned} B(t)&= \frac{A_2}{c_1-c_2}x_3 \left( c_1\alpha _{o1}x_1+c_2\alpha _{o2}x_2\right) , \end{aligned}$$
(12)
$$\begin{aligned} S(t)&= \frac{A_2}{c_1-c_2}x_3\left[ c_1\alpha _{o1}\alpha _xx_1+ \alpha _c\left( c_1x_1-c_2x_2\right) \right] , \end{aligned}$$
(13)
$$\begin{aligned} K(t)&= \frac{A_2}{c_1-c_2}x_3\left[ c_2\alpha _{o2}\alpha _Kx_2- \alpha _c\left( c_1x_1-c_2x_2\right) \right] .\end{aligned}$$
(14)

Hence one may express (5) as

$$\begin{aligned} H=H_{1n}\,+\,A(t)\,\tilde{H}_2\,+\,H_\Delta \end{aligned}$$
(15)

where

$$\begin{aligned}&H_\Delta =-\Xi (t)\,\frac{1}{a^3}\,-\,\psi (t)\,\frac{1}{a}, \end{aligned}$$
(16)
$$\begin{aligned}&A(t)= \frac{c_0B(t)}{1+c_0x(t)}~,~~ \tilde{H}_2= \frac{\alpha _b}{a^{\frac{3}{2}}}+ \frac{\alpha _r}{a^2}, \end{aligned}$$
(17)
$$\begin{aligned}&\Xi (t)= \frac{c_0S(t)}{1+c_0x(t)},~~ \psi (t)= \frac{c_0K(t)}{1+c_0x(t)} .\end{aligned}$$
(18)

We let

$$\begin{aligned}&H_{1n0}=\tilde{\Omega }_1^\frac{1}{2}H_0,~~ A_0\alpha _b=\tilde{\Omega }_b^{\frac{1}{2}}H_0,~~ \,A_0\alpha _r=\tilde{\Omega }_r^{\frac{1}{2}}H_0,\nonumber \\&\Xi _0=\tilde{\Omega }_x^{\frac{1}{2}}H_0,~~ \,\psi _0=\tilde{\Omega }_K^{\frac{1}{2}}H_0 \end{aligned}$$
(19)

where \(H_{1n0}=H_{1n}(t_0)\), \(H_0=H(t_0)\), \(A_0=A(t_0)\), \(\Xi _0=\Xi (t_0)\), \(\psi _0=\psi (t_0)\). Because the three-dimensional part of metric is taken to be flat the present energy density is equal to the critical energy density, and the above equations imply that

$$\begin{aligned} \tilde{\Omega }_1^\frac{1}{2}\,+\, \tilde{\Omega }_b^{\frac{1}{2}}\,+\, \tilde{\Omega }_r^{\frac{1}{2}}\,-\, \tilde{\Omega }_x^{\frac{1}{2}}\,-\, \tilde{\Omega }_K^{\frac{1}{2}}=1. \end{aligned}$$
(20)

Note that at this point \(\tilde{\Omega }_1\), \(\tilde{\Omega }_b\), \(\tilde{\Omega }_r\), \(\tilde{\Omega }_x\), \(\tilde{\Omega }_K\) cannot be identified as density parameters since density parameters should satisfy \(\Omega _1\)+\(\Omega _b\)+\(\Omega _r\)+\(\Omega _x\)+\(\Omega _K=1\). In Chapter IV we will see that this condition is not satisfied for the phenomenologically viable sets of parameters, so \(\tilde{\Omega }_1\), \(\tilde{\Omega }_x\), \(\tilde{\Omega }_K\) cannot be identified as density parameters separately, instead one must define the total density parameter for dark sector by \(\Omega _D^\frac{1}{2}=\tilde{\Omega }_1- \tilde{\Omega }_x-\tilde{\Omega }_K\) rather than the separate contribution due to \(H_{1n}\) and \(H_\Delta \) while we identify \(\tilde{\Omega }_b\), \(\tilde{\Omega }_r\) as the density parameters corresponding dust and radiation. Therefore to retain the physical content of this paper more evident we will not make a distinction between \(\tilde{\Omega }_b\), \(\tilde{\Omega }_r\) and the density parameters for baryonic matter and radiation; \(\Omega _b\), \(\Omega _r\), while we keep this distinction for the others, i.e., for the ones due to the \(H_{1n}\) and \(H_\Delta \) terms. The \(\frac{\alpha _b}{a^\frac{3}{2}}\) and \(\frac{\alpha _r}{a^2}\) terms result in energy densities that are identified as the energy densities for baryonic matter and radiation. In principle, there may also be contributions due to the \(\Xi \frac{1}{a^3}\) and \(\psi \frac{1}{a}\). The sign of the \(\Xi \frac{1}{a^3}\) term is negative of the usual stiff matter. It may be identified as stiff matter under pressure so that it has a negative deceleration parameter. The main function of this term is to dampen the energy densities of baryonic matter and radiation in the time before the radiation dominated era. The function of the \(\frac{1}{a}\) term is similar. It ensures the behavior of the energy density in late times be well behaved (i.e. preventing the energy density to grow too fast (through the \(\frac{1}{a}\) term in \(x_2(t)\) and \(x_3(t)\))). Although the \(\psi \frac{1}{a}\) term is similar to that of a negative curvature 3-space it is different from such a term since its origin is the Hubble parameter \(H\) while a usual 3-curvature term arises from the 3-curvature part of metric. Note that this term arises even in a flat 3-space in this construction. Therefore we identify the \(\frac{\Xi }{a^3}\) and \(\frac{\psi }{a}\) terms in \(H\) as additional contributions to dark sector.

Another point worth to mention is; It is evident that the square of (5) (in conjunction with (10)) results in an \(A^2\tilde{H}_{2}^2\) term containing \(A^2\frac{\alpha _b^2}{a^3}\) and \(A^2\frac{\alpha _r^2}{a^4}\) terms, which may be identified with the standard baryonic matter and radiation terms, respectively if \(A\) is taken to be constant, while it depends on time in this scheme as is evident from (7). In fact variation of \(A\) with time makes it possible to go to zero before the radiation dominated era as desired. Therefore, given the considerable success of the standard model at least in the observed relatively small redshifts, the variation in \(A\) after the matter–radiation decoupling time should be small so that this scheme mimics the standard model at relatively small redshifts where observational data is available. If one takes \(\left( \frac{dA}{dt}\right) _{t\simeq \,t_0}\) sufficiently small one may guarantee an almost constant value for \(A\) for a sufficiently long time (e.g. from the present time till the beginning of the radiation dominated era). We will see in Sect. 4 that there exist such values of \(A\) with reasonable phenomenological viability. Another term arising from \(\tilde{H}_2^2\) is the cross term, \(A^2\frac{\alpha _b\alpha _r}{a^\frac{7}{2}}\). This term may be identified as the energy density term due to the transitory time where massive particles that act as radiation at high energies turn into more dust-like entities at intermediate energies. Another term in \(H^2\) is \(H_{1n}^2\). This term will be considered as a pure dark sector term. Finally the cross term \(2H_{1n}\tilde{H}_2\) gives an additional contribution to the dark sector for the phenomenologically viable values of the parameters. It may easily be shown that this term does not necessarily imply strong interaction between the dark fluid and radiation and baryonic matter as its form may suggest if the parameters of the underlying physics at microscopic scale satisfy some restrictions. Otherwise one may use screening mechanisms such as [50–55] to explain the unobservability of dark matter-energy.

Next we derive the general form of the equation of state for this model. We derive the explicit form of the equation of state after (EOS) after we give the explicit form of \(a_1(t)\) in the section. However, giving the general form of EOS in this scheme provides us a more model independent formula and may be useful for other choices of \(a_1(t)\) in future. After using Eqs. (15–18) one obtains EOS, \(\omega \) as

$$\begin{aligned} \omega&= \frac{p}{\rho }=\frac{\frac{G_{11}}{g_{11}}}{G_{00}}= -\frac{2\dot{H}+3H^2}{3H^2} \nonumber \\&= -\frac{2\dot{H}_{1n}\,+\,3H_{1n}^2}{3H^2} \,-\,\frac{AH_{1n}\left( \frac{3\alpha _b}{a^\frac{3}{2}}+\frac{2\alpha _r}{a^2} \right) }{3H^2} \nonumber \\&+\frac{A^2\left( \frac{\alpha _r^2}{a^4} +\frac{\alpha _b\alpha _r}{a^\frac{7}{2}}\right) }{3H^2} \,-\,\frac{2\dot{A}\tilde{H}_2}{3H^2}\nonumber \\&+\frac{A\left( \frac{\Xi }{a^3}+\frac{\psi }{a}\right) \left( \frac{3\alpha _b}{a^\frac{3}{2}}+\frac{2\alpha _r}{a^2}\right) }{3H^2}+ \frac{6H_{1n}\left( \frac{\Xi }{a^3}+\frac{\psi }{a}\right) }{3H^2}\nonumber \\&-\, \frac{2H\left( \frac{3\Xi }{a^3}+\frac{\psi }{a}\right) \,+\,3 \left( \frac{\Xi ^2}{a^6}+\frac{\psi ^2}{a^2}+\frac{2\Xi \psi }{a^4}\right) }{3H^2}. \end{aligned}$$
(21)

The terms inside the first parentheses in the second line correspond to the contribution of the dark sector term \(H_{1n}\). The other terms in the same line correspond to the contributions of dust and radiation and their coupling with dark sector term \(H_{1n}\). The remaining terms are the term corresponding to variation of \(A\), the term corresponding to coupling of curvature-like term and the stiff matter under negative pressure with dust and radiation, the term corresponding to coupling of curvature-like term and the stiff matter under negative pressure with \(H_{1n}\), the term corresponding to coupling of curvature-like term and the stiff matter under negative pressure with the other terms, and the contribution of the curvature-like term and the stiff matter under negative pressure, respectively. It is evident from (21) that the pressure for baryonic matter is zero as it should be, and the pressure for radiation is \(\frac{1}{3}\) as expected. A point worth to mention at this point is; The coupling term between baryonic matter and radiation in Eq. (21) has an equation of state \(\frac{1}{6}\) (which may be seen by considering the ratio of the \(\frac{\alpha _b\alpha _r}{a^\frac{7}{2}}\) in \(p\) by the corresponding term in \(\rho \) i.e. \(2\frac{\alpha _b\alpha _r}{a^\frac{7}{2}}\)). The redshift dependence of this term is between that of baryonic matter and radiation. This time dependence is more natural than the standard picture where there is no such term. Massive particles at high energies act as radiation and at lower energies turn into dust. The coupling term accounts for the transitory time when massive particles pass from the radiation to the dust state.

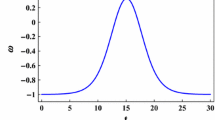
In order to obtain the evolution of \(\omega \) as a function redshift or time explicitly, \(H_{1n}\) must be specified. This will be done in the next section. However, we give a \(\omega \) versus redshift graph in Fig. 1 for \(a_{1n}\) introduced in the next section for a phenomenologically viable set of parameters (i.e. those with small \(\chi ^2\) values and with energy densities for recombination and nucleosynthesis as discussed in Sect. 4) to have an idea about the evolution of \(\omega \) with redshift. To draw this graph we have converted time, t to redshift, z (for the Union2.1 data) through the relation \(z=\frac{1}{a}-1\), and then used Mathematica to use this relation to make the calculations (although the original quantities are expressed in terms of time). This procedure is applicable for small redshifts. However, in general, it becomes inapplicable due to highly nonlinear form of scale factor and Hubble parameter since it requires huge RAM and CPU for computation, if it can be done at all, and hence requires a separate computational physics project by itself. Therefore we have used equation of state versus and energy density versus time graphs (instead of redshift) in Sect. 4. In fact, even that option required a long time of order of months to make the necessary computations.

Fig. 1
figure 1

\(\omega \) versus redshift z graphs for \(\Lambda \)CDM (for PDG and Planck values) and for this model (for two sets of parameters with small \(\chi ^2\) values), namely, for \(\Lambda \)CDM with \(\Omega _\Lambda =0.6825\), \(\Omega _b=0.3136\), \(\Omega _r=1.3\times \,10^{-3}\) (solid green) and with \(\Omega _\Lambda =0.73\), \(\Omega _b=0.2661\), \(\Omega _r=1.3\times \,10^{-3}\) (dashed black); and for this model for the set of parameters (solid blue) and for the set of parameters (\(r=1.58\), \(s=5.3\), \(\beta =3.1\), \(\Omega _b^\frac{1}{2}=0.21\), \(\xi i_1=0.975\), \(A_1=c_1=\alpha _{o2}=1\), \(A_2=10^{-4}\), \(c_2=0.999\), \(\frac{\alpha _r}{\alpha _b}=0.1\), \(\alpha _{ac}=0.05\), \(\alpha _{o1}=0.9\), \(\frac{\alpha _x}{\alpha _b}= \frac{\alpha _K}{\alpha _b}=0.7\)) (dotted red). Here the subindex \(b\) refers to dust

Full size image

3 An explicit realization of the model

Now we focus on the \(a_1(t)\) term. We take

$$\begin{aligned} a_1(t)&= A_1a_{1n}(t), \end{aligned}$$
(22)
$$\begin{aligned} a_{1n}(t)&= [p_1\,+\,p_2b_2t]^r\,\exp {[-b_1(b_2t)^{-1/s}]} \end{aligned}$$
(23)

where \(A_1\,<\,1\), \(p_1\), \(p_2\), \(b_2\), \(b_1\) are some constants that to be fixed or bounded by consistency arguments or cosmological observations. This scale factor is a generalization of the scale factor in [42] where \(r=1\), \(s=6\). A similar scale factor is considered in [56] as well. One of the shortcomings of [42] is that the present value of the equation of state parameter in that model (for phenomenologically relevant choices of parameters where the model mimics \(\Lambda \)CDM) is \(\sim -0.4\), while the observations imply that it should be \(\simeq (-0.68) - (-0.74)\) [48, 49]. In the present study there is an additional contribution due to mixing of the terms due to \(a_1\) and \(a_2\) and hence there is less need to modify the scale factor in [42]. However, we prefer to adopt the more general form in (23) to seek a greater parameter space and to ensure the correct equation of state parameter.

We have shown in Eq. (5) that the Hubble parameter may be expressed as \(H=H_{1n}\,+\,A(t)\,\tilde{H}_2\,+\,H_\Delta \). Now we concentrate on the \(H_{1n}=\frac{\dot{a}_{1n}}{a_{1n}}\) part of the Hubble parameter. In fact, this amounts to specifying the model wholly, since the other terms, as well, depend on \(a_{1n}\) as we have seen. The corresponding \(H_{1n}\) is given by

$$\begin{aligned} H_{1n}(t)= \frac{\dot{a}_{1n}}{a_{1n}} =\frac{rp_2b_2}{(p_1+p_2b_2t)} +\frac{1}{s}b_2b_1(b_2t)^{-\left( 1+\frac{1}{s}\right) }.\quad \end{aligned}$$
(24)

We let

$$\begin{aligned} 1=a_{1n0}=a_{1n}(t_0)= (p_1+p_2b_2t_0)^r \exp {[-b_1(b_2t_0)^{-\frac{1}{s}}]}\nonumber \\ \end{aligned}$$
(25)

and

$$\begin{aligned} H_{0}t_0=\xi ,~~~ (p_1+p_2b_2t_0)^r = \exp {[b_1(b_2t_0)^{-\frac{1}{s}}]}= \beta >1,\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned} H_{1n0}t_0&= H_{1n}(t_0)t_0=\frac{rp_2b_2t_0}{(p_1+p_2b_2t_0)} +\frac{1}{s}b_1(b_2t_0)^{-\frac{1}{s}} \nonumber \\&= \xi \xi _1\,\Rightarrow ~~~~ rp_2b_2t_0=\beta ^{\frac{1}{r}}\left( \xi \xi _1-\frac{1}{s}\ln {\beta }\right) ,\nonumber \\ p_1&= \beta ^{\frac{1}{r}}\left[ 1-\frac{1}{r}\left( \xi \xi _1-\frac{1}{6}\ln {\beta }\right) \right] ,\end{aligned}$$
(27)
$$\begin{aligned}&\Rightarrow ~~~ H_1(t)=H_{1n}(t)=H_{1n}(\gamma )\nonumber \\&=\frac{1}{t_0}\left\{ \frac{\xi \xi _1-\frac{1}{s}\ln {\beta }}{[1+\frac{\gamma -1}{r}(\xi \xi _1-\frac{1}{s}\ln {\beta })]} +\frac{1}{s}\gamma ^{-\frac{s+1}{s}}\ln {\beta }\right\} \end{aligned}$$
(28)

here \(\gamma =\frac{t}{t_0}\) where \(t_0\) is the present age of the universe. One observes from (19) and the above expression that

$$\begin{aligned} H_{1n0}=\tilde{\Omega }_1^\frac{1}{2}H_0=\frac{1}{t_0}\xi \xi _1 ~~\Rightarrow ~~\tilde{\Omega }_1^\frac{1}{2}=\xi _1 .\end{aligned}$$
(29)

We will see in the next section that \(\tilde{\Omega }_1\) cannot be identified as the density parameter corresponding to \(H_{1n}\). Instead one must define an overall density parameter for the dark sector by \(\Omega _D^\frac{1}{2}\)= \(\tilde{\Omega }_1^\frac{1}{3}- \tilde{\Omega }_x^\frac{1}{3}- \tilde{\Omega }_K^\frac{1}{3}\). The observational values of \(H_0=\left( \frac{\dot{a}}{a}\right) _{t=t_0}\) and \(\frac{1}{t_0}\) are almost the same. Therefore \(\xi ^2\xi _1^2\,\simeq \,\xi _1^2\).

After determining the \(H_{1n}\) we are almost ready to find the explicit values of the energy density and the equation of state. The only missing element for calculation of these quantities is to find \(A\), \(\Xi \), \(\psi \) in Eqs. (15–18). Another point to be addressed is to show that there exist sets of A whose variation with time are small for low redshifts, so that the terms that are proportional to \(\frac{1}{a^\frac{3}{2}}\) and \(\frac{1}{a^2}\) in \(A\,\tilde{H}_2\) term may be identified with dust and usual radiation terms, respectively.

In order to determine \(A\), \(\Xi \), \(\psi \) (and to determine the rate of variation of \(A\) with time) one should derive an approximation scheme for the evaluation of these quantities because these quantities depend on \(x_1(t)\), \(x_2(t)\), \(x_3(t)\) (which are defined in Eqs. (8) and (9)), and these quantities, in turn, are defined in a recursive way since \(x_i(t)=\exp {(\int _{t_0}^t\tilde{H}_2^{(i)}\mathrm{d}t)}\) (\(i=1,2,3\)) and \(\tilde{H}_2^{(i)}\) depend on \(a(t)\), and \(a(t)\), in turn, depends on \(x_i(t)\) through Eq. (4). In other words, in order to determine the approximate values of \(x_i(t)\) one must identify the zeroth order approximation and a method of how to obtain the higher order approximations in an iterative way. One may use the following observations to obtain the zeroth order approximation: \(A_1c_0(1+c_0x(0))^{-1}=A_1\frac{1}{A_1-A2}(1+\frac{A_2}{A_1-A_2})^{-1}=1\) and \(\dot{A}\sim \,0\) \(\Leftrightarrow \) \(\dot{x}_i\sim \,0\) (\(i=1,2,3\)) i.e. \(\dot{x}\sim \,0\), \(x(t)\simeq \,x(0)=1\) for small redshifts. This implies that the zeroth order approximation for the scale factor \(a(t)\) should be taken as \(a^{(0)}(t)=a_{1n}(t)\) Hence for phenomenologically viable cases (where \(\dot{A}\sim \,0\) for small redshifts) one may take the zeroth order approximations as

$$\begin{aligned} x_i^{(0)}(t)=\exp {\int _{t_0}^t\tilde{H}_2^{(i0)}\mathrm{d}t}\quad i=1,2,3 \end{aligned}$$
(30)

where \(\tilde{H}_2^{(10)}\), \(\tilde{H}_2^{(20)}\), \(\tilde{H}_2^{(30)}\) is obtained from \(\tilde{H}_2^{(1)}\), \(\tilde{H}_2^{(2)}\), \(\tilde{H}_2^{(3)}\) by replacing \(a(t)\) by \(a_{1n}(t)\) in those expression, for example,

$$\begin{aligned} \tilde{H}^{(10)}_2 =\alpha _{o1}\alpha _b\displaystyle \int \nolimits _{t_0}^t\left\{ -\frac{1}{a_{1n}^{\frac{3}{2}}}- \frac{\frac{\alpha _r}{\alpha _b}}{a_{1n}^2}+ \frac{\frac{\alpha _x}{\alpha _b}}{a_{1n}^3}\right\} .\end{aligned}$$
(31)

Then

$$\begin{aligned}&A^{(0)}(t)= \frac{c_0B^{(0)}(t)}{1+c_0x^{(0)}(t)} ,\end{aligned}$$
(32)
$$\begin{aligned}&x^{(0)} (t)=\frac{A_2}{c_1-c_2}x_3^{(0)} (c_1x_1^{(0)}-c_2x_2^{(0)}) ~etc. \end{aligned}$$
(33)

One may get the next order approximation by using

$$\begin{aligned} a(t)\simeq \,a^{(1)}(t)= c_0A_1(1+c_0x^{(0)})^{-1} a_{1n} .\end{aligned}$$
(34)

The next order quantities \(A^{(1)}\), \(x^{(1)}\) may be obtained from (32) and (33) by replacing the superindices \((0)\) by \((1)\) where

$$\begin{aligned} x_i^{(1)}(t)=\exp {\int _{t_0}^t\tilde{H}_2^{(i1)}\mathrm{d}t} .\end{aligned}$$
(35)

Here \(\tilde{H}_2^{(i1)}\) is obtained from \(\tilde{H}_2^{(i)}\) by replacing \(a(t)\) by \(a^{(1)}(t)= c_0A_1(1+c_0x^{(0)})^{-1} a_{1n}\). For the \(k\)th approximation we replace \(a(t)\) by \(a^{(k)}(t)= c_0A_1(1+c_0x^{(k-1)})^{-1} a_{1n}\). In principle, this may be done up to arbitrarily higher order approximations but it is quite difficult to calculate even \(A^{(1)}\) even with the help of computers. In fact we have divided the interval \(t\,-\,t_0\) into coarser subintervals to decrease the CPU time and have used the approximate numerical values in the \(i\)th interval (by assuming \(A^{(0)}\) to be almost constant in those intervals) by using the formula

$$\begin{aligned} A^{(0)}(t_i)=\frac{A^{(0)}(t_{i-1})\,+\, A^{(0)}(t_{i+1})}{2} \end{aligned}$$
(36)

to find \(A^{(1)}\). We have seen (by trial and error) that it is possible to find almost constant \(A^{(0)}\) and \(A^{(1)}\) values for many relevant (i.e. of small \(\chi ^2\) values as considered in the next section) choices of parameters, \(\alpha _b\), \(r\), \(s\), \(\xi _1\), \(\xi _1\), \(A_1\), \(A_2\), \(c_1\), \(c_2\), \(\alpha _r\), \(\alpha _c\), \(\alpha _{o1}\), \(\alpha _{o2}\), \(\alpha _x\), \(\alpha _K\). For example the variations of \(A^{(0)}\) and \(A^{(1)}\) with time for one of the phenomenologically viable sets in Table 3 is given in Table 1.

Table 1 The zeroth and the first order approximations to \(A(t)\): \(A^{(0)}(t)\) and \(A^{(1)}(t)\) as a function \(\gamma =\frac{t}{t_0}\) for the set of parameters, \(r=.138, s=12, \beta =3.3, \xi _1\xi =0.975, A_1=1, A_2=0.002745, c_1=1, c_2=0.9986, \frac{\alpha _r}{\alpha _b}=0.03, \alpha _c=10^{-7}, \alpha _{o1}=0.5, \alpha _{o2}=1, \frac{\alpha _x}{\alpha _b}=1, \frac{\alpha _K}{\alpha _b}=0.8, \Omega _b^\frac{1}{2}=0.22\). Note that first order value \(A^{(1)}\) for \(\gamma =10^{-8}\) and smaller values of \(\gamma \) are not evaluated since the iteration procedure is not applicable for such small times because of the time intervals, \(t_i-t_{i-1}=0.1\,t_0\), that we have used in Eq. (36) is much coarser than \(10^{-8}\)
Full size table

4 Compatibility with observations

Now we check the phenomenological viability of the model. The observational analysis of the model for all possible values of the parameters, \(\beta \), \(r\), \(s\), \(\xi \), \(\xi _1\), etc. is an extremely difficult job (if not impossible at all) because expressing the Hubble parameter, deceleration parameter etc. in terms of the scale factor is quite difficult since these quantities are highly nonlinear functions of the scale factor in this model. Therefore we adopt some guidelines to seek the phenomenologically viable sets of parameters. These guidelines are:

  1. 1.

    We take the model to mimic the standard model, i.e., the \(\Lambda \)CDM model, at least from the time of decoupling of matter and radiation up to the present time. Therefore we take the present time values of the equation of state of the whole universe and the density parameter of the baryonic matter and radiation to be the same as \(\Lambda \)CDM.

  2. 2.

    In searching for the phenomenologically viable parameter space we start from the values of the parameters in [42] i.e. \(r=1\), \(s=6\), \(\xi =1\), and \(\beta \sim \,O(1)\) since the universe studied in [42] mimics the true universe roughly.

  3. 3.

    Due to the highly nonlinear relation between the Hubble parameter and the scale factor we seek the relevant parameter space usually by trial and error rather than a continuous scan of the parameter space. Therefore the optimum values obtained here most probably may not correspond to the best possible optimization. Rather they hopefully correspond to a good approximation to the best optimal values.

4.1 Compatibility with Union2.1 data

In this subsection we use the Union2.1 compilation data set to find the optimal values of \(\beta \), \(r\), \(s\) starting from \(\beta =3\), \(r=1\), \(s=6\). We find the theoretical values of distance moduli, \(\mu \) for the redshift values of Union2.1 and calculate the corresponding \(\chi ^2\) value by using the measured values of \(\mu \) and their errors.

The expression for distance modulus is

$$\begin{aligned} \mu = 5\,\mathrm{Log}_{10}\left( \frac{d_L}{1\,\mathrm{Mpc}}\right) \,+\,25 \end{aligned}$$
(37)

where

$$\begin{aligned} d_L=\frac{c\,a_0}{a(t)}\int _t^{t_0}\frac{\mathrm{d}t^\prime }{a(t^\prime )}{=} \frac{c\,a_0}{\frac{A_1c_0}{1+c_0x(t)}a_{1n}(t)} \int _t^{t_0}\frac{dt}{\frac{A_1c_0}{(1+c_0x(t^\prime ))}a_{1n}(t^\prime )} \end{aligned}$$
(38)

where for small redshifts reduces to

$$\begin{aligned} d_L\simeq \frac{c}{a_{1n}(t)}\int _t^{t_0}\frac{\mathrm{d}t^\prime }{a_{1n}(t^\prime )} \end{aligned}$$
(39)

where we have used the requirement that \(\frac{A_1c_0}{1+c_0x}\simeq \,1\) at small redshifts as discussed in the preceding section (see Table 2), and \(a_0=a(0)=1\). In \(\Lambda \)CDM \(\int \frac{dt}{a(t)}\) is usually expressed in terms of redshift, \(z\) and Hubble parameter \(H\), and then the results for different \(z\)’s are compared with the data directly. This is not possible in this model because \(H\) cannot be expressed in terms of \(a(t)\) in a simple way. Therefore in this study first we convert redshift values of Union2 to time values by using \(z= \frac{1}{a(\gamma )}-1\simeq \, \frac{1}{a_{1n}(\gamma )}-1\) and then solve it for \(\gamma \). The corresponding expression for the theoretical value of the luminosity distance \(d_L\) in this case (i.e. in terms of \(\gamma \)) is

$$\begin{aligned} d_L&\simeq \frac{c\,t_0\, \beta ^{-1+\gamma ^{-\frac{1}{s}}}}{\left[ 1+\frac{\gamma -1}{r}\left( \xi \xi _1 -\frac{1}{s}\ln {\beta }\right) \right] ^r}\nonumber \\&\times \int _\gamma ^1 \mathrm{d}\gamma \frac{\beta ^{-1+\gamma ^{-\frac{1}{s}}}}{\left[ 1+\frac{\gamma -1}{r}\left( \xi \xi _1-\frac{1}{s}\ln {\beta }\right) \right] ^r} \end{aligned}$$
(40)

where \(a_{1n}(t)\) is expressed in terms of \(\beta \), \(r\), \(s\), \(\gamma =\frac{t}{t_0}\) by using the parameterization given in the preceding section. Equation (40) may be written in a more standard form in terms of \(H_0\) by using \(H_0t_0=\xi \). Then we find Eq. (39) numerically for each of the \(\gamma \) corresponding to observational redshifts. Finally we find the corresponding \(\chi _0^2\) values by using the formula

$$\begin{aligned} \chi _0^2=\sum _{i=1}^{i=580}\left\{ \frac{((\mu ^{th(0)}(\gamma (i),r,s,\beta ,\xi \xi _1,t_0) -\mu ^\mathrm{obs}_i)^2}{\left( \sigma _i\right) ^2}\right\} \quad \end{aligned}$$
(41)

where the subscript \(0\) in \(\chi _0\) and the superscript \((0)\) in \(\mu ^{th(0)}\) stands for the fact that \(a(t)\) is approximated by its zeroth order approximation, i.e. by \(a_{1n}\); the superindices \(th\) and \(obs\) stand for the theoretical and observational values of \(\mu \), and the subindices \(i\) denote the values of the corresponding quantity for the \(i\)th data point in the Union2 data set.

Table 2 \(\zeta (t)\)=\(\frac{(1+c_0x)}{c_0A_1}\) versus \(\gamma =\frac{t}{t_0}\) values for the set of the parameters; \(r=2.138, s=12, \beta =3.3, \xi _1\xi =0.975, A_1=c_1=\alpha _{o2}=1, A_2=0.002745, c_2=0.9986, \alpha _{o1}=0.5, \frac{\alpha _r}{\alpha _b}=0.03, \alpha _c=10^{-7}, \frac{\alpha _x}{\alpha _b}=1, \frac{\alpha _K}{\alpha _b}=0.8, t_0=\,\frac{1}{72.8}\) (Mpc/km) s, \(\chi _0^2=579.97, \chi ^2=576.69\). Note that \(\frac{\zeta _{av}}{\zeta _0}\simeq \,\)0.9996 is rather close to 1 where \(\zeta _{av}\), \(\zeta _0\) are the average value of \(\zeta \) and the value of \(\zeta \) at \(\gamma =1\), respectively
Full size table

One may try a better approximation by replacing \(a_{1n}(t)\) in (39) by a better approximation of \(a(t)\) i.e. by \(\frac{c_0A_1}{1+c_0x^{(0)}(t)}a_{1n}(t)\) where \(x^{(0)}(t)\) is defined by Eq. (31). In principle, then, one may evaluate the integral (38) after replacing \(a_{1n}(t)\) by \(\frac{c_0A_1}{1+c_0x^{(0)}(t)}a_{1n}(t)\). However, this seems to be inapplicable for standard computers because of the complicated form of the integral. One needs a separate computational physics project for this aim. Instead one may try a rough approximation (hopefully better than \(a_{1n}\)); we take the \(\frac{1+c_0x^{(0)}}{c_0A_1}\) term in the integral to outside of the integral with its \(\gamma \) value being the bound of the integral. This approximation is a good approximation provided that \(\frac{c_0A_1}{1+c_0x(t)}\) does not vary much in the time interval between \(t_0\) and the time corresponding to the given redshift value. Otherwise the higher order approximation may worsen the approximation rather than improving it. The corresponding formulas (in the first order approximation) become

$$\begin{aligned}&d_L\,\simeq \, \left( \frac{1+c_0x^{(0)}}{c_0A_1}\right) ^2\frac{c\,t_0\, \beta ^{-1+\gamma ^{-\frac{1}{s}}}}{\left[ 1+\frac{\gamma -1}{r}\left( \xi \xi _1 -\frac{1}{s}\ln {\beta }\right) \right] ^r} \nonumber \\&\quad \times \int _\gamma ^1 \mathrm{d}\gamma \frac{\beta ^{-1+\gamma ^{-\frac{1}{s}}}}{\left[ 1+\frac{\gamma -1}{r}\left( \xi _1 -\frac{1}{s}\ln {\beta }\right) \right] ^r} ,\end{aligned}$$
(42)
$$\begin{aligned} \chi ^2=\sum _{i=1}^{i=580}\left\{ \frac{(( \mu ^\mathrm{th}(\gamma (i),r,s,\beta ,\xi \xi _1,t_0) -\mu ^\mathrm{obs}_i)^2}{(\sigma _i)^2}\right\} .\end{aligned}$$
(43)

By trial and error we have found many sets of parameters with relatively small \(\chi _0^2\), \(\chi ^2\) values. For example the \(\chi _0^2\), \(\chi ^2\) values for two phenemonologically viable sets of parameters are given in Table 3 where the reduced \(\chi _0^2\), \(\chi _\mathrm{red\,0}^2=\frac{\chi _0^2}{580-5}\), and the reduced \(\chi ^2\) values \(\chi _\mathrm{red}^2=\frac{\chi }{580-12}\) are in the order of 1 (where 580 is the number of data points, and 5, 12 are the number of free parameters \(r\), \(s\), \(\beta \) etc. to be adjusted).

Table 3 Some of the sets of parameters with sufficient energy densities for recombination and nucleosynthesis with relevant redshift values. Here \(\gamma _\mathrm{rc}=\frac{t_\mathrm{rc}}{t_0}\), \(\gamma _\mathrm{ns}=\frac{t_\mathrm{ns}}{t_0}\); the subscripts rc and ns denote recombination and nucleosynthesis, respectively; A\(\equiv \) (\(r=2.138\), \(s=12\), \(\beta =3.3\), \(\xi \xi _1=0.975\), \(\xi =1\), \(\Omega _b^\frac{1}{2}=0.22\), \(A_1=1\), \(A_2=0.002745\), \(c_1=1\), \(c_2=0.9986\), \(\frac{\alpha _r}{\alpha _b}=0.03\), \(\alpha _c=10^{-7}\), \(\alpha _{o1}=0.3\), \(\alpha _{o2}= 1\), \(\frac{\alpha _x}{\alpha _b}=1\), \(\frac{\alpha _K}{\alpha _b}=0.8\)). The set B is the same as the set A except \(\alpha _{o1}\) is replaced by 0.5. The best \(\chi ^2\) values for the sets A and B correspond to \(t_0=\frac{1}{72.9\,\mathrm{km}\,\mathrm{s}^{-1}\,\mathrm{Mpc}^{-1}}\,\simeq \,13.25\) years and \(t_0=\frac{1}{72.8\,\mathrm{km}\,\mathrm{s}^{-1}\,\mathrm{Mpc}^{-1}}\simeq \,13.3\) years, respectively. Note that the shape of the \(\omega \) versus \(\gamma \) is extremely sharp in time; hence the location of \(\left( \frac{\rho _{r}}{\rho _{r0}}\right) _\mathrm{ns}\) is sensitive to the exact value of \(\gamma \). The more exact values of \(\gamma \) for the set A and B where \(\omega \) is minimum are (\(\gamma \simeq \,3.67027978907089\times \,10^{-11}\), \(\gamma \simeq \,3.31606438849865\times \, 10^{-14}\)) and (\(\gamma \simeq \,7.1641402601557\times \,10^{-11}\), \(\gamma \simeq \,2.246997272913787\times \,10^{-14})\)), respectively. A similar case is true for \(\gamma _\mathrm{ns}\) since it is extremely small. The more exact values of \(\gamma _\mathrm{ns}\) for the set A and B are (\(1.498712948305\times \,10^{-11}\), \(3.1102\times \,10^{-14}\)), (\(2.8422577892672\times \,10^{-11}\), \(3.06971839\times \,10^{-14}\)), respectively
Full size table

The sets of parameters (which we could find by trial and error) with relatively small \(\chi ^2\) values satisfy \(c_1\simeq \,c_2\,\simeq \,1\), \(\alpha _c\ll \,1\). By using this information one may check the validity of (20) and determine if one may identify \(\tilde{\Omega }_1\), \(\tilde{\Omega }\), \(\tilde{\Omega }_K\) by the corresponding density parameters; \(\Omega _1\), \(\Omega _x\), \(\Omega _K\) for the phenomenologically relevant parameters by using Eqs. (19), (17), and (18). We observe that \(x(0)=A_2, x_1(0)=x_2(0)=x_3(0)=1, c_1=1\) and for relevant values of the parameters. Hence, after using Eq. (19), we obtain

$$\begin{aligned} \frac{\tilde{\Omega }_x^\frac{1}{2}}{\Omega _b^\frac{1}{2}}&\simeq \left( \frac{\alpha _{o1}}{\alpha _{o1}+\alpha _{o2}}\right) \left( \frac{\alpha _x}{\alpha _b}\right) ,\nonumber \\&\frac{\tilde{\Omega }_K^\frac{1}{2}}{\Omega _b^\frac{1}{2}}\,\simeq \, \left( \frac{\alpha _{o2}}{\alpha _{o1}+\alpha _{o2}}\right) \left( \frac{\alpha _K}{\alpha _b}\right) .\end{aligned}$$
(44)

We observe that for phenomenologically viable sets of parameters, for example, for those in Table 3, we have \(\tilde{\Omega }_x^\frac{1}{2}\,\sim \,\tilde{\Omega }_K^\frac{1}{2}\,\sim \, \frac{1}{2}\Omega _b^\frac{1}{2}\) and (20) may be satisfied since \(\tilde{\Omega }_1^\frac{1}{2}\)= \(\xi _1\,\simeq \,0.98 \sim \,1\). We notice that \((\tilde{\Omega }_1^\frac{1}{2} +\Omega _b^\frac{1}{2}+\Omega _r^\frac{1}{2} +\tilde{\Omega }_x^\frac{1}{2} +\tilde{\Omega }_K^\frac{1}{2})^2 \,\ne \,1\). However, one may define a total density parameter for the dark sector by

$$\begin{aligned} \Omega _D^\frac{1}{2}= \tilde{\Omega }_1^\frac{1}{2} -\tilde{\Omega }_x^\frac{1}{2} -\tilde{\Omega }_K^\frac{1}{2} .\end{aligned}$$
(45)

Then the density parameters satisfies the necessary condition, \((\Omega _D^\frac{1}{2}+\Omega _b^\frac{1}{2}+\Omega _r^\frac{1}{2})^2=1\). In other words, \(H_{1n}\) and \(H_\Delta \) terms cannot be identified as separate contributions to dark sector, rather they must be considered as just a single object in order not to introduce an ambiguity in their identification.

4.2 Compatibility with recombination and nucleosynthesis

In this subsection we investigate if this model is compatible with the cosmological depiction of the recombination and nucleosynthesis, at least, at the order of magnitude level. In a similar vein as the preceding subsection we require this model mimic the standard model, \(\Lambda \)CDM, as much as possible. We assume that the radiation and the baryonic matter are in thermal equilibrium in the eras of recombination and nucleosynthesis since we adopt the same equations of thermal equilibrium as \(\Lambda \)CDM. Therefore, in the following, first we derive the condition for thermal equilibrium for this model. Then we find the sets of parameters with least \(\chi ^2\) values that may produce successful recombination and nucleosynthesis eras. The correct choices should have sufficient radiation energy densities in these eras. In other words the redshift at the recombination time, \(z_{re}\) should be in the order of \((1+z_{re})^4\,>\, (1+z_*)^4\,\simeq \,(1{,}100)^4\) where * denotes time of last scattering surface; and in the nucleosynthesis era the energy density of neutrinos should reach energy densities of the order of \((1\,\mathrm{MeV})^4\). We seek an approximate, rough agreement with \(\Lambda \)CDM since the search of the parameter space is done by trial and error rather than a systematic search of the whole parameter space. Therefore a detailed, thorough analysis and compatibility survey would be too ambitious especially considering this is a toy model.

Before checking if there exist a set of parameters compatible with recombination and nucleosynthesis we should check if the thermal equilibrium is maintained in these eras in for the given set of parameters because we adopt the standard analysis in \(\Lambda \)CDM, and that analysis assumes existence of thermal equilibrium. As is well known, if there is thermal equilibrium then we should have \(\Gamma \,>\,H\) where \(\Gamma \) is the rate of the interaction between radiation and the matter and \(H\) is the Hubble parameter. However, the implementation of this condition in this model is not exactly the same as in \(\Lambda \)CDM. In the case of the recombination era the implementation of this condition does not give exactly the same result as \(\Lambda \)CDM since, in \(\Lambda \)CDM the recombination takes place in radiation dominated era and the total energy density is almost wholly due to radiation while, in this model, the total energy density of the universe at this era is not almost wholly due to radiation although the equation of state parameter for phenomenologically relevant cases is similar that of radiation dominated universe at the time of recombination and we require the radiation energy density to be the same or almost the same as \(\Lambda \)CDM. In the case of nucleosynthesis, even the equation state parameter in this model does not mimic that of a radiation dominated universe. Therefore we should derive the corresponding conditions for thermal equilibrium for this model.

The condition for thermal equilibrium in the recombination era is

$$\begin{aligned}&\Gamma \,>\,H~\Rightarrow \,~1.97\times \,10^{-19}s^{-1}\nonumber \\&\times \,0.0227\, \left( \frac{T}{T_{ph\,0}}\right) \,>\,\alpha _1\,H_0\Omega _{ph}^\frac{1}{2} \nonumber \\&\Rightarrow ~ \left( \frac{\frac{\rho }{\rho _0}}{\frac{\rho _{ph}}{\rho _{ph0}}} \right) ^\frac{1}{2}\,<\, 0.19\,\left( \frac{T}{T_{ph\,0}}\right) =0.19(1+z_{re}).\nonumber \\ \end{aligned}$$
(46)

Here we have used the identities

$$\begin{aligned}&\alpha _1^2=\frac{\rho }{\rho _{ph}} =\frac{1}{\Omega _{ph}}\left( \frac{\frac{\rho }{\rho _0}}{\frac{\rho _{ph}}{\rho _{ph0}}}\right) ,\quad \frac{\rho _r}{\rho _{r0}}=\frac{\rho _{ph}}{\rho _{ph0}}=a^{-4} \end{aligned}$$
(47)

where \(\alpha _1\simeq \,1\) is the \(\Lambda \)CDM value and \(\alpha _1^2\le \,1\) at the time of recombination and is not constant in this model, and we have used the PDG values, \(H_0=72\,\mathrm{km}\,\mathrm{Mpc}^{-1}\,s^{-1}\), \(\Omega _{ph}=4.8\times \,10^{-5}\). Note that \(\Gamma \) in Eq. (46) is the same as the \(\Lambda \)CDM value while \(H\) is different from the \(\Lambda \)CDM value.

Next consider the condition on thermal equilibrium at and before the time of nucleosynthesis. In thermal equilibrium we have

$$\begin{aligned}&\frac{\Gamma _\nu }{H}\approx \frac{1}{\alpha _2}\frac{\sqrt{45}G_{wk}^2}{64\pi ^3}\sqrt{\frac{hc^5}{G}} (k_BT)^3 \,\simeq \,\frac{1}{\alpha _2}\left( \frac{T}{10^{10}K}\right) ^3>1 \nonumber \\&\Rightarrow \left( \frac{\frac{\rho }{\rho _0}}{\frac{\rho _r}{\rho _{r0}}} \right) ^\frac{1}{2}\,<\, \Omega _r^\frac{1}{2}\left( \frac{T}{10^{10}\,\mathrm{K}}\right) ^3 \end{aligned}$$
(48)

where we have used the identity similar to (47), where \(\alpha _1\) and the subindex ph are replaced by \(\alpha _2\) and \(r\), respectively and the ratio is evaluated at the time of nucleosynthesis. In this case, as well, \(\Gamma _\nu \) is the same as its \(\Lambda \)CDM value while the expression for \(H\) in terms of temperature is different since \(\alpha _2\le \,1\) and is not a constant (i.e. it gives a different value when evaluated at different time during nucleosynthesis) in this model while \(\alpha _2=1\) in \(\Lambda \)CDM. During thermal equilibrium the ratio of neutrinos to all nucleons, \(X_n\) is given by

$$\begin{aligned} X_n=\frac{1}{1+\exp {\left( \frac{Q}{k_BT}\right) }} \end{aligned}$$
(49)

where \(Q\) is the rest mass energy difference between a neutron and a proton, \(Q=m_n-m_p=1.239\, MeV\). After the thermal equilibrium between the neutrinos and the nucleons are lost i.e. after decoupling the value of \(X_n\) further decreases due to decay of free neutrons as

$$\begin{aligned} X_n=X_{n0}\exp {\left[ -\left( \frac{t}{\tau _0}\right) \right] } \end{aligned}$$
(50)

where \(X_{n0}\) is the \(X_n\) of Eq. (49) at the time of decoupling, and \(\tau _0=885.7\) s is the lifetime of a free neutron. Therefore the effect of this model is to change the value of \(X_{n0}\) (which depends on \(\alpha _2\)) and probably the value of \(X_n\) as well.

Now we are ready to check the viability of this model. We could give only four graphs and three tables that partially summarize the results of my calculations related to this and the next paragraphs in order not to expand the size of the paper too much. Otherwise the size of the manuscript would be almost doubled. First we check the viability of the model for recombination and nucleosynthesis eras. To this end we have used Eqs. (17, 18, 21, 28) in the zeroth order approximation where \(a(t)\simeq \,a_{1n}(t)\) (as discussed before Eq. (30)) to draw \(\omega \), \(\frac{\rho _r}{\rho _{r0}}\), versus time graphs by using a Mathematica code that we have prepared for this aim for the sets of the parameters, \(r\),\(s\),\(\beta \),\(\xi \xi _1\), \(A_1\), \(A_2\), \(c_1\), \(c_2\), \(\frac{\alpha _r}{\alpha _b}\),\(\frac{\alpha _x}{\alpha _b}\), \(\frac{\alpha _K}{\alpha _b}\), \(\alpha _c\),\(\alpha _{o1}\), \(\alpha _{o2}\), \(t_0\) \(\Omega _b^\frac{1}{2}\), that correspond to some relatively small \(\chi ^2\) values obtained in preceding subsection. Then we have tried to find at least one set of parameters with phenomenologically viable \(\omega _0\), \(\frac{\rho _r}{\rho _{r0}}\), \(\frac{\rho }{\rho _0}\) values i.e. \(\omega _0\), in the range \(-0.68\,-\) \(-0.74\); \(\frac{\rho _r}{\rho _{r0}}\,>\,(1{,}100)^2\simeq \,10^{12}\) (in the range of redshifts \(z\sim \,800~-~3{,}000\)) at the time of recombination, and \(\frac{\rho _r}{\rho _{r0}}\,>\,\frac{(1\,\mathrm{MeV})^4}{5\times \,10^{-5}\,(2.5\times \,10^{-3}\,\mathrm{eV})^4}\,>\,10^{38}\) at the time of nucleosynthesis where we have approximated \(x_1(t)\), \(x_2(t)\), \(x_3(t)\) by \(x_1^{(0)}(t)\), \(x_2^{(0)}(t)\), \(x_3^{(0)}(t)\) (which are defined in Eq. (30)), and \(a(t)\) by \(a_{1n}(t)\) (which is defined in Eq. (23)) as discussed in the preceding section. We have found two sets of parameters given in Table 3 that satisfy these conditions. A comment is in order at this point. The zeroth order approximation is reliable only for small redshifts. However, this approximation is reliable at any redshift if one is only interested in the energy density–redshift relation. This may be seen as follows: Assume that the energy density \(\rho \) is related to redshift \(z\) by \(\rho =f(z)\) in the zeroth order approximation (where \(f(z)\) is an arbitrary function), and in an approximation better than the zeroth order we have \(\frac{c_0A_1}{A_1-A_2}=\frac{1}{x}\) i.e. \(a(t)=\frac{1}{x}a_{1n}(t)\). Then the energy density after the correction is \(\rho ^\prime =f(z^{\prime })\). If one rescales \(z^\prime \) as \(\frac{1}{x}z^\prime =z\) then one obtains the same redshift and energy density values. In other words the redshift–energy density relation is invariant under such corrections. However, this is not true for the redshift–time relation. If the approximation is not a good approximation to the true value then the redshift–time relation will be distorted. This, in turn, may cause the distortion of the value of the equation of state and the distortion of the variation of the energy densities with time in an amount depending on the reliability of the zeroth order approximation. Keeping these observations in mind we are content to use a zeroth order approximation for the times of recombination and nucleosynthesis because even employing a zeroth order approximation needs a lot of computer CPU and RAM, and in many cases the use of a first order approximation neither does improve the situation. We will come back to these points when we discuss the times of recombination and nucleosynthesis.

Next we have checked if thermal equilibrium is maintained at the times of recombination and nucleosynthesis and if recombination and nucleosynthesis are realized in this model. One may have an idea on thermal equilibrium at the time of recombination by using the values of Table 3 at \(z\simeq \,1{,}100\) and Eq. (46). However, a more rigorous way is to draw \(\left( \frac{\frac{\rho }{\rho _0}}{\frac{\rho _r}{\rho _{r0}}}\right) ^\frac{1}{2} \left( \frac{1}{0.19 \frac{T}{T_{ph0}}}\right) \) (which may be obtained from Eq. (46)) versus time graphs to determine the time intervals (and then the corresponding redshift intervals) where \(\left( \frac{\frac{\rho }{\rho _0}}{\frac{\rho _r}{\rho _{r0}}}\right) ^\frac{1}{2} \left( \frac{1}{0.19\frac{T}{T_{ph0}}}\right) \le \,1\) for each of the sets A and B. In fact we have used \(\frac{T}{T_{ph0}}=1+z\) for the relevant redshifts. The resulting intervals are the intervals where thermal equilibrium is maintained as shown in Fig. 4 for the set B in Table 3. The smallest redshifts where the thermal equilibrium is lost are \(z=2{,}317\) (\(\gamma =1.615\times \,10^{-10} \) with \(\frac{\rho _r}{\rho _{r0}}\,\simeq \,5.52\times \,10^{13}\)) and \(z=1{,}625\) (\(\gamma =2.82\times \,10^{-10}\) \(\frac{\rho _r}{\rho _{r0}}\,\simeq \,3\times \,10^{13}\)) for the sets A and B, respectively. This implies that the photon–electron decoupling takes place before the time of last scattering at an energy of \(\simeq \,2{,}317\times \,6\times \,10^{-4}\) eV\(\,\simeq \,1.4\) eV and \(\simeq \,1{,}625\times \,6\times \,10^{-4}\) eV\(\,\simeq \,0.98\) eV for the sets A and B, respectively (assuming the transition to be directly to the ground state of hydrogen atom) to be compared to the value of photon energy of about \(\simeq \,1{,}100\times 6\times \,10^{-4}\) eV\(\,\simeq \,0.66\) eV for \(\Lambda \)CDM at the time of last scattering. This, in turn, implies that photon–electron decoupling in this model for the sets of parameters A and B is at a smaller redshift than \(\Lambda \)CDM where thermal equilibrium is maintained until decoupling. (Thermal equilibrium would be maintained till \(z\simeq \,2.4\) in \(\Lambda \)CDM if recombination of electrons and protons to form neutral atoms had not taken place as may be seen from (46) by setting \(\alpha _1=1\)). In fact the corresponding times for decoupling are already smaller than that of \(\Lambda \)CDM by five orders of magnitude. A detailed comprehensive separate study is need to see if these imply some interesting phenomenologically viable alternatives or just an artifact of the toy model and/or the sets of parameters considered. This may also be due to the limitation of the applicability of the zeroth order approximation that we have discussed above. \(a(t)\simeq \,a_{1n}(t)\) is not violated badly at the time of recombination for the most of the relevant sets of parameters. For example for the sets of parameters given in Table 3 the first order approximation results in \(a(t)\simeq \,0.4\,a_{1n}(t)\) i.e. \(\frac{c_0A_1}{A_1-A_2}\simeq \,0.4\) and does not vary much at the time of recombination. Therefore it seems that the effect of the limitation of the applicability of the zeroth order approximation to the time of recombination must be limited. However, this shift does not introduce a major problem, since the redshift values, hence the photon energy density at recombination, remains almost the same and thermal equilibrium is maintained. Next we have checked if thermal equilibrium is maintained at the peaks in Table 3 where the energy densities are sufficient for nucleosynthesis. We have used Eq. (48) to find the range of temperatures where thermal equilibrium is maintained. We have found that this condition is satisfied for \(T\,>\,3\times \,10^{10}\,\mathrm{K}\) (provided that \(\Omega _r\simeq \,5\times \,10^{-5}\)) for the second peaks. This value gives us \(X_{n0}\) in Eq. (50) by using Eq. (49) as \(X_{n0}\simeq \,0.39,\) which is quite large compared to the for \(\Lambda \)CDM value of \(\simeq 0.25\). The time that it takes \(3\times \,10^{10}K\simeq \,1\,MeV\) to drop to 0.07 MeV (that is, when \(\frac{\rho _r}{\rho _{r0}}\,\sim \,10^{32}\)) in this model is something like \(\sim 2\times \,10^{-16}\times \,t_0\simeq \,90\) s. Therefore \(X_{n0}\) does not drop significantly through Eq. (50). In other words the final result \(X_{n}\simeq \,0.35\) is much larger than the \(\Lambda \)CDM value \(\simeq \,0.13\) (which agrees well with observations). Probably the main source of this discrepancy is the inapplicability of zeroth order approximations to redhifts and energy densities to this era to obtain correct energy density–time relations. The variations of \(\frac{c_0A_1}{A_1-A_2}\) and \(A\) are quite large and their values are quite different from those at \(z\sim \,0\) at the time of nucleosynthesis, which makes the applicability of the zeroth order approximation extremely difficult to obtaining the correct energy density–time relation. In other words the main source of the discrepancy may be due to the fact that the real time of free decay may be of the order of \(\sim 1{,}000\) s in this model instead of 90 s. The use of a first order approximation does not improve the situation because in the calculation of first order approximations to \(\frac{c_0A_1}{A_1-A_2}\) and \(A(t)\) one uses the zeroth order approximation \(a(t)\,\simeq \,a_{1n}(t)\) in the integrals for \(x_i\), \(i=1,2,3\). This, in turn, results in an over-contribution of large redshifts and hence larger and more varying \(x_i\) with respect to their true values since \(x_i\,<1\) and they get smaller, i.e. \(\frac{c_0A_1}{A_1-A_2}\) gets larger at larger redshifts. Therefore the energy density versus time graphs in Figs. 2, 3, and 4 must be considered with some care. The time values in those graphs should be taken with utmost care especially in the case of nucleosynthesis, while the magnitudes of energy densities and the corresponding redshifts are expected to be the same as the exact values. All these points must be studied in more detail in future studies. However, we have been able to show that this scheme can produce a model that mimics the standard model: there is a current accelerated epoch whose present equation of state (for the whole universe) is \(-0.7\) (that is, at least roughly, in agreement with observations; e.g. see the values in Table 3 for a phenomenologically relevant set of parameters). Before this epoch \(\omega \) changes sign and the time near this sign change may be considered as the matter dominated era. Although the sign change of \(\omega \) occurs at a later time in this model compared to \(\Lambda \)CDM the time and the redshift of onset of the accelerated era (i.e. \(\omega \simeq \,-\frac{1}{3}\)) are comparable with those of \(\Lambda \)CDM. There is an epoch before the matter dominated era where \(\omega \) is on average close to \(\frac{1}{3}\), and may be identified by radiation dominated era, and the time of the maximum value of \(\omega \) may be considered as the time when the universe was like stiff matter or denser (as in the cores of stars). Then \(\omega \) changes sign again reaches two minimum peaks as mentioned before and eventually approaches to \(-1\) as time goes to zero (due to the \(H_{1n}\), in particular the first part of it and this epoch probably may be considered as the inflationary era. Moreover, the model is able to give relatively small reduced \(\chi _0^2\) and \(\chi ^2\) values for the Union2.1 data set, and it can, at least roughly, account for recombination and nucleosynthesis times. We think this is a sufficiently good starting point for a toy model whose main aim is to embody the creation of matter and radiation in the scale factor of Robertson–Walker metric. However, there are a great deal of points to be clarified and addressed in future studies, such as checking the whole parameter space of this model by using a more elaborate software and to use more powerful computers that may give a scan of the whole parameter space in a better approximation than the one given here, and considering a more detailed analysis of the recombination and nucleosynthesis epochs, studying the evolution of cosmological perturbations in this model, and considering possible extensions of this model toward a more realistic model.

Fig. 2
figure 2

\(\omega \) (dotted blue), \(\frac{\rho }{\rho _0}\) (dot-dashed red), \(\frac{\rho _x}{\rho _{x0}}\) (solid black), \(\frac{\rho _r}{\rho _{r0}}\) (dashed green), \(\frac{\rho _b}{\rho _{b0}}\) (solid yellow) versus \(\gamma =\frac{t}{t_0}\) graphs for the set B in Table 9 for the first energy density peak in the interval \(2.8422577892 \times \,10^{-11}\,\le \,\gamma \le \, 2.8422577894\times \,10^{-11}\). In this graph \(\omega \), \(\frac{\rho }{\rho _0}\), \(\frac{\rho _r}{\rho _{r0}}\), \(\frac{\rho _b}{\rho _{b0}}\) are given as multiples of \(10^4\), \(10^{28}\), \(10^{31}\), \(10^{23}\), \(10^{19}\), respectively

Full size image
Fig. 3
figure 3

\(\omega \) (dotted blue), \(\frac{\rho }{\rho _0}\) (dot-dashed red), \(\frac{\rho _x}{\rho _{x0}}\) (solid black), \(\frac{\rho _r}{\rho _{r0}}\) (dashed green), \(\frac{\rho _b}{\rho _{b0}}\) (solid yellow) versus \(\gamma =\frac{t}{t_0}\) graphs for the set B in Table 9 for the second energy density peak in the interval \(10^{-15}\,\le \,\gamma \le \, 10^{-13}\). In this graph \(\omega \), \(\frac{\rho }{\rho _0}\), \(\frac{\rho _r}{\rho _{r0}}\), \(\frac{\rho _b}{\rho _{b0}}\) are given as multiples of 10, \(10^{28}\), \(10^{31}\), \(10^{27}\), \(10^{20}\), respectively

Full size image
Fig. 4
figure 4

\(\left( \frac{\frac{\rho }{\rho _0}}{\frac{\rho _r}{\rho _{r0}}}\right) ^\frac{1}{2} \left( \frac{1}{0.19 \frac{T}{T_{ph0}}}\right) \) versus \(\gamma \) graph in the interval where thermal equilibrium is maintained for the set B in Table 3 in the interval \(10^{-12}\, \le \,\gamma \le \, 2.82\times \,10^{-10}\)

Full size image

5 Conclusion

In this study a scheme for obtaining a scale factor (in Robertson–Walker metric) that may account for the times before, during, and after the radiation dominated eras is introduced. The prescription to obtain the scale factor in this model is quite simple; First one introduces a scale factor for the pure dark sector, and then the full scale factor is obtained by a relation between these two scale factors. The result is a scheme to produce the scale factor for the whole universe, including baryonic matter, radiation, and dark energy–matter (i.e. dark sector) in such a way that the times before, during, and after radiation dominated era are expressed by a single scale factor in Robertson–Walker metric. Different choices of the pure dark sector scale factor (denoted by \(a_1\) in this paper) and different choices of the relation between \(a_1(t)\) and the scale factor of the full universe, \(a(t)\) give different models. As an illustration of this scheme a model with a specific scale factor for the pure dark sector and a specific relation between \(a_1(t)\) and \(a(t)\) is considered. The phenomenological viability of this model is checked through its compatibility with Union2.1 data set, and with recombination and nucleosynthesis by using trial and error and Mathematica software for almost randomly chosen sets of parameters. Two sets of parameters with relatively small \(\chi ^2\) values for the Union2.1 data set and that are compatible with successful recombination and nucleosynthesis at an order of magnitude level are found. These results are encouraging in view of the fact that only a tiny portion of the whole parameter space could be considered in this way. A separate, detailed, and comprehensive computational project with more advanced software codes and/or powerful computing facilities that may scan the full parameter space and may employ better approximation schemes is needed to reach a definite view on the observational viability of this scheme and/or this model. Moreover, the effect of this model on cosmological perturbations should be considered and possible implications and extensions of this scheme to the inflationary era should be studied in future. Furthermore, different pure dark sector scale factors and different options to relate the pure dark sector and the full universe scale factors may be considered in future to see the full range of possibilities that this scheme may offer.