Maxwell–Chern–Simons vortices in a CPT-odd Lorentz-violating Higgs electrodynamics

Abstract

We study BPS vortices in a CPT-odd and Lorentz-violating Maxwell–Chern–Simons–Higgs (MCSH) electrodynamics attained from the dimensional reduction of the Carroll–Field–Jackiw–Higgs model. The Lorentz-violating parameter induces a pronounced behavior at origin (for the magnetic/electric fields and energy density) which is absent in the MCSH vortices. For some combination of the Lorentz-violating coefficients there always exists a sufficiently large winding number $n_{0}$ such that for all $|n|\ge |n_{0}|$ the magnetic field flips sign, yielding two well-defined regions with opposite magnetic flux. However, the total magnetic flux remains quantized and proportional to the winding number.

1 Introduction

Vortex configurations constitute an important branch of research, common to condensed matter and high energy physics. This interconnection was established since the seminal works by Abrikosov [1] and Nielsen–Olesen [2], which demonstrated the existence of electrically neutral vortices in type-II superconducting systems and in field theory models, respectively. Since then, vortex solutions have become a theoretical field of increasing interest, reinforced with the works arguing the existence of BPS (Bogomol’nyi–Prasad–Sommerfeld) solutions [3, 4]. BPS vortices were found in the Chern–Simons–Higgs model [5–8] and in the Maxwell–Chern–Simons–Higgs (MCSH) model [9], with additional investigations involving nonminimal coupling [10, 11] and other aspects [12–14]. Recently the existence has been shown of generalized Maxwell–Higgs and Chern–Simons vortices [15–17] in the context of k-field theories [18–24], which have been a fertile environment for studying new topological defects solutions [25, 26]. The existence of charged BPS vortices in a generalized Maxwell–Chern–Simons–Higgs model was also demonstrated in Ref. [27], while the duality between vortices and planar Skyrmions in BPS theories has also been addressed [28]. Unusual vortex configurations in condensed matter systems, endowed with magnetic flux reversion [29] and fractional quantization [30–32], have also caught attention in the latest years.

Lorentz-violating theories have been the focus of strong interest since the proposal of the standard model extension (SME) [33–43], whose gauge sector was intensively scrutinized in many respects [44–67]. The study of topological defects in Lorentz-violating (LV) scenarios was initially conducted for defects in scalar systems [68–71]. The existence of monopole solutions in the presence of Lorentz violation was considered in the context of the Carroll–Field–Jackiw electrodynamics [72, 73]. Topological defects were also examined in a broader framework of field theories endowed with tensor fields that spontaneously break the Lorentz symmetry [74, 75]. One investigation about oscillon and breather solutions modified by LV terms was also reported [76].

The pioneering investigation about BPS vortex solutions in the presence of CPT-even Lorentz-violating terms of the SME was performed in Refs. [77, 78], following the idea of finding new defect solutions in modified theoretical frameworks. In Ref. [77], uncharged BPS vortices were found in an Abelian Maxwell–Higgs model supplemented with CPT-even Lorentz-violating terms belonging to the Higgs and gauge sectors of the SME. The Lorentz-violating BPS vortices are compactlike and could present fractional quantization of the magnetic flux. In a similar context, it was shown that the parity-odd sector of the CPT-even term $( K_{F})^{\mu \alpha \nu \beta }$ allows the existence of electrically charged BPS vortices in the absence of the Chern–Simons term [78], endowed with magnetic flux reversion. The study of vortex configurations in Lorentz-violating models has been an issue of active investigation recently [79–82].

So far, no investigation as regards BPS vortex configurations was performed in a CPT-odd and Lorentz-violating environment. The aim of this paper is to study BPS vortices in the Lorentz-violating planar Maxwell–Carroll–Field–Jackiw electrodynamics, trying to describe the BPS vortex solutions supported by this planar version of CPT-odd gauge sector of the SME. We highlight the characteristics of the corresponding BPS solutions, which possess the property of magnetic flux reversion: a remarkable feature induced by Lorentz violation, which may find applications in some vortex systems of condensed matter physics [29–32]. We start from a planar Lorentz-violating Maxwell–Chern–Simons model attained via the dimensional reduction of the CPT-odd Maxwell–Carroll–Field–Jackiw electrodynamics coupled to the Higgs sector, examined in Ref. [83]. In Sect. 2, we present the model and implement the BPS formalism to attain the self-dual first order equations describing the topological vortices. In Sect. 3, we use the vortex Ansatz to show that our solutions satisfy the usual boundary conditions and behave as Abrikosov–Nielsen–Olesen vortices. Also, the results of the numerical analysis are presented, revealing charged vortex profiles that recover the MCSH solutions in the asymptotic region, and which may strongly differ from the ones near the origin. Finally, in Sect. 4, we make some remarks and give our conclusions.

2 The theoretical model and BPS formalism

The Maxwell–Carroll–Field–Jackiw–Higgs model [83] in $(1+3)$ dimensions is given by

$$\begin{aligned} \mathcal {L}&= -\frac{1}{4}F_{\hat{\mu }\hat{\nu }}F^{\hat{\mu }\hat{\nu }} -\frac{1}{4}\epsilon ^{\hat{\mu }\hat{\nu }\hat{\rho }\hat{\sigma }}( k_{\mathrm{AF}}) _{\hat{\mu }}A_{\hat{\nu }}F_{\hat{\rho }\hat{\sigma } }\nonumber \\&+\vert D_{\hat{\mu }}\phi \vert ^{2}-V(\vert \phi \vert ), \end{aligned}$$

(1)

where $\hat{\mu },\hat{\nu },\hat{\rho },\hat{\sigma }=0,1,2,3$. The first term, $F_{\hat{\mu }\hat{\nu }}=\partial _{\hat{\mu }}A_{\hat{\nu }}-\partial _{\hat{\nu } }A_{\hat{\mu }}$, is the electromagnetic strength-tensor, and $A_{\hat{\mu }}$ is the gauge field. The second term, $\epsilon ^{\hat{\mu }\hat{\nu }\hat{\rho }\hat{\sigma }}( k_{\mathrm{AF}}) _{\hat{\mu }}A_{\hat{\nu }} F_{\hat{\rho }\hat{\sigma }}$, is the CPT-odd and Lorentz-violating Carroll–Field–Jackiw (CFJ) term. The Higgs field $\phi$ couples to the gauge field via the covariant derivative $D_{\hat{\mu }}\phi =\partial _{\hat{\mu }} \phi -ieA_{\hat{\mu }}\phi$.

The dimensional reduction to $(1+2)$ dimensions is performed as follows. First, all fields are considered as independent of the $\hat{3}$-coordinate, $\partial _{\hat{3}}f=0$. The third component of the gauge field is promoted to be a neutral scalar field, $A_{\hat{3}}=\psi \rightarrow A_{\hat{\mu }}=( A_{\mu },\psi )$. The same rule is applied for the third component of the CFJ vector background, $( k_{\mathrm{AF}}) _{\hat{3}}=s\rightarrow (k_{\mathrm{AF}}) _{\hat{\mu }}=( ( k_{\mathrm{AF}}) _{\mu },s)$, with $s$ being a scalar. Such a procedure provides a kind of MCSH model modified by Lorentz-violating (LV) terms which play the role of coupling constants between the neutral scalar field $( \psi )$ and the abelian gauge field $(A_{\mu })$. Thus, the Lorentz-violating MCSH model is described by the following Lagrangian density:

$$\begin{aligned} \mathcal {L}&= -\frac{1}{4}F_{\mu \nu }F^{\mu \nu }+\frac{1}{4}s\,\epsilon ^{\nu \rho \sigma }A_{\nu }F_{\rho \sigma }+\vert D_{\mu }\phi \vert ^{2}\nonumber \\&+\frac{1}{2}\partial _{\mu }\psi \partial ^{\mu }\psi -e^{2}\psi ^{2}\vert \phi \vert ^{2}-U(\vert \phi \vert ,\psi )\nonumber \\&-\frac{1}{2}\epsilon ^{\mu \rho \sigma }(k_{\mathrm{AF}}) _{\mu }A_{\rho }\partial _{\sigma }\psi -\frac{1}{2}\epsilon ^{\mu \rho \sigma }( k_{\mathrm{AF}}) _{\mu }\psi ~\partial _{\rho }A_{\sigma }, \end{aligned}$$

(2)

where the Lorentz-violating parameter $s=(k_{\mathrm{AF}}) _{\hat{3}}$ plays the role of a Chern–Simons coupling, $( k_{\mathrm{AF}}) _{\mu }$ is the $(1+2)$-dimensional CFJ vector background which couples the neutral and gauge fields. Here, $D_{\mu }\phi =\partial _{\mu }\phi -ieA_{\mu }\phi$ defines the covariant derivative, $e$ represents the electromagnetic coupling constant. The potential $U(\vert \phi \vert ,\psi )$ that provides BPS solutions will be determined below.

The stationary Gauss law and Ampère law are

$$\begin{aligned} \partial _{j}\partial _{j}A_{0}-sB-\epsilon _{ij}( k_{\mathrm{AF}}) _{i}\partial _{j}\psi =2e^{2}A_{0}\vert \phi \vert ^{2}, \end{aligned}$$

(3)

$$\begin{aligned} \epsilon _{kj}\partial _{j}B-s\epsilon _{kj}\partial _{j}A_{0}+( k_{\mathrm{AF}}) _{0}\epsilon _{kj}\partial _{j}\psi =eJ_{k}, \end{aligned}$$

(4)

where $J_{k}$ is the spatial component of the current density, $J^{\mu }=i[\phi ( D^{\mu }\phi ) ^{*}-\phi ^{*}D^{\mu } \phi ]$.

The stationary equations of motion of the Higgs and neutral fields read

$$\begin{aligned} 0&= \partial _{k}\partial _{k}\phi -2ieA_{k}\partial _{k}\phi +e^{2}( A_{0})^{2}\phi \nonumber \\&-e^{2}(A_{k}) ^{2}\phi -e^{2}\psi ^{2}\phi -\frac{\partial U}{\partial \phi ^{*}}, \end{aligned}$$

(5)

$$\begin{aligned} 0&= \partial _{j}\partial _{j}\psi -(k_{\mathrm{AF}}) _{0} B-\epsilon _{ij}(k_{\mathrm{AF}}) _{i}\partial _{j}A_{0} \nonumber \\&-2e^{2}\psi \vert \phi \vert ^{2}-\frac{\partial U}{\partial \psi }, \end{aligned}$$

(6)

respectively.

The stationary energy density $(\mathcal {E})$ associated with Lagrangian (2) is

$$\begin{aligned} \mathcal {E}&= \frac{1}{2}(\partial _{j}A_{0}) ^{2}+\frac{1}{2}B^{2}+\vert D_{j}\phi \vert ^{2}+\frac{1}{2}( \partial _{j}\psi ) ^{2}\nonumber \\&+e^{2}A_{0}^{2}\vert \phi \vert ^{2}+e^{2}\psi ^{2}\vert \phi \vert ^{2}+U, \end{aligned}$$

(7)

where the condition $(k_{\mathrm{AF}}) _{0}=0$ was imposed in order to ensure the positiveness of the energy density. Thus, in the present approach, only spatial components of the $(1+2)$-dimensional Carroll–Field–Jackiw vector background contribute.

In the following we focus our attention on the development of a BPS framework [3, 4] which provides first order differential equations consistent with the second order equations (3)–(6). So, by using the identity

$$\begin{aligned} \vert D_{j}\phi \vert ^{2}=\vert D_{\pm }\phi \vert ^{2}\pm e\vert \phi \vert ^{2}B\pm \frac{1}{2}\epsilon _{ab}\partial _{a}J_{b}, \end{aligned}$$

(8)

with $D_{\pm }\phi =D_{1}\phi \pm iD_{2}\phi$, and converting the energy to a sum of quadratic terms, it becomes

$$\begin{aligned} \mathcal {E}&= \frac{1}{2}[ B\mp \sqrt{2U}] ^{2}+\vert D_{\pm }\phi \vert ^{2}+\frac{1}{2}(\partial _{j}A_{0}\pm \partial _{j}\psi ) ^{2}\nonumber \\&+e^{2}\vert \phi \vert ^{2}( A_{0}\pm \psi ) ^{2}\pm B\sqrt{2U}\pm e\vert \phi \vert ^{2}B\nonumber \\&\mp ( \partial _{j}A_{0}) (\partial _{j}\psi ) \mp 2e^{2}\vert \phi \vert ^{2}A_{0}\psi \pm \frac{1}{2}\epsilon _{ab}\partial _{a}J_{b}. \end{aligned}$$

(9)

The energy density (9) is minimized by imposing the requirement that the quadratic terms must be null, which leads to the BPS equations of this model,

$$\begin{aligned} D_{\pm }\phi&= 0,\end{aligned}$$

(10)

$$\begin{aligned} B&= \pm \sqrt{2U},\end{aligned}$$

(11)

$$\begin{aligned} A_{0}&= \mp \psi ,\end{aligned}$$

(12)

$$\begin{aligned} \partial _{j}A_{0}&= \mp \partial _{j}\psi . \end{aligned}$$

(13)

The condition

$$\begin{aligned} \psi =\mp A_{0} \end{aligned}$$

(14)

solves the last two BPS equations. It is similar to that appearing in the context of the MCSH vortex configurations [9, 12–14]. Taking into account Eqs. (10)–(13), the BPS energy density becomes

$$\begin{aligned} \mathcal {E}&= \pm B\sqrt{2U}\pm e\vert \phi \vert ^{2}B+(\partial _{j}A_{0}) ^{2}\nonumber \\&+2e^{2}\vert \phi \vert ^{2}(A_{0}) ^{2}\pm \frac{1}{2}\epsilon _{ab}\partial _{a}J_{b}, \end{aligned}$$

(15)

and Gauss’s law reads

$$\begin{aligned} {\partial _{j}\partial _{j}A_{0}-sB\pm \epsilon _{ij}( k_{\mathrm{AF}}) _{i}\partial _{j}A}_{0}{=2e^{2}A_{0}\vert \phi \vert ^{2}.} \end{aligned}$$

(16)

By using Gauss’s law, Eq. (15) can be written in a very convenient form:

$$\begin{aligned} \mathcal {E}=\pm B\sqrt{2U}\pm e\vert \phi \vert ^{2}B-sBA_{0} +\partial _{a}\mathcal {J}_{a}, \end{aligned}$$

(17)

with $J_{a}$ defined as

$$\begin{aligned} \mathcal {J}_{a}=\pm \frac{1}{2}\epsilon _{ab}J_{b}+A_{0}\partial _{a}A_{0} \mp \frac{1}{2}\epsilon _{ab}(k_{\mathrm{AF}})_{b}A_{0}^{2}. \end{aligned}$$

(18)

In order to attain a BPS energy density proportional to the magnetic field plus a total derivative, we can choose the potential as

$$\begin{aligned} U=\frac{1}{2}(ev^{2}-e\vert \phi \vert ^{2}\pm sA_{0})^{2}, \end{aligned}$$

(19)

so that the energy density becomes

$$\begin{aligned} \mathcal {E}_{\mathrm{BPS}}=\pm ev^{2}B+\partial _{a}\mathcal {J}_{a}. \end{aligned}$$

(20)

Here, the term $v^{2}$ represents the vacuum expectation value of the Higgs field. After integrating under appropriate boundary conditions (see Eqs. (25) and (26)), the BPS energy,

$$\begin{aligned} E_{\mathrm{BPS}}={\pm }ev^{2}\int \mathrm{d}^{2}rB={\pm }2\pi v^{2}n, \end{aligned}$$

(21)

turns out to be proportional to the quantized magnetic flux, $\Phi _{B}=2\pi n/e,$where $n$ is the winding number of the vortex configuration.

Thus, the BPS formalism leads to the self-dual equations of this model,

$$\begin{aligned}&D_{\pm }\phi =0,\end{aligned}$$

(22)

$$\begin{aligned}&B=\pm ( ev^{2}-e\vert \phi \vert ^{2}) +sA_{0}, \end{aligned}$$

(23)

which are the same ones as those of the MCSH model [9]. These two equations and the Gauss law (16) describe topological vortices in this Lorentz-violating MCSH framework.

3 Charged vortex configurations

Specifically, we look for axially symmetric solutions using the standard static vortex Ansatz,

$$\begin{aligned} \phi =vg(r) e^{in\theta },~A_{\theta }=-\frac{a(r) -n}{er},~A_{0}=A_{0}(r), \end{aligned}$$

(24)

where $n$ represents the winding number of the topological vortex, the scalar functions $a(r), g(r)$ and $A_{0}(r)$ are regular in $r=0$ and at $r\rightarrow \infty$. As usual, the fields $g$and $a$ satisfy the following boundary conditions:

$$\begin{aligned} g(0) =0,\;a(0) =n, \end{aligned}$$

(25)

$$\begin{aligned} g(\infty ) =1,\,a(\infty ) =0. \end{aligned}$$

(26)

The boundary conditions satisfied by the field $A_{0}$ will be explicitly established in subsection 3.1.

The Ansatz (24) allows one to express the magnetic field in a simple way:

$$\begin{aligned} B=-\frac{a^{\prime }}{er},x \end{aligned}$$

(27)

with the short-hand notation $a^{\prime }\equiv \mathrm{d}a/\mathrm{d}r$. The BPS equations (22,23) are rewritten as

$$\begin{aligned} g^{\prime } =\pm \frac{ag}{r}, \end{aligned}$$

(28)

$$\begin{aligned} B=-\frac{a^{\prime }}{er}=\pm ev^{2}(1-g^{2}) +sA_{0}, \end{aligned}$$

(29)

whereas the Gauss law (16) reads

$$\begin{aligned} A_{0}^{\prime \prime }+\frac{A_{0}^{\prime }}{r}\!-\!sB\mp ( k_{\mathrm{AF}}) _{\theta }\left( A_{0}^{\prime }\!+\!\frac{A_{0}}{2r}\right) -2e^{2}v^{2}g^{2}A_{0}\!=\!0. \end{aligned}$$

(30)

Here, the upper (lower) sign corresponds to $n>0$ ($n<0$). Note that $(k_{\mathrm{AF}}) _{\theta }$ is the only component of the $(1+2)$-dimensional Carroll–Field–Jackiw background compatible with axially symmetric solutions, that is, $(k_{\mathrm{AF}}) _{\theta }$ is the only CFJ component remaining in the equations above describing the BPS solutions after the Ansatz (24) is implemented. Note that it does not mean that the radial component $( k_{\mathrm{AF}})_{r}$ was taken as null; it simply does not participate in the formation of axially symmetric vortices. This fact was also observed in the parity-odd coefficients $\kappa _{0i}$ of the symmetric tensor $\kappa _{\mu \nu }$ of the LV and CPT-even model analyzed in Ref. [78], where only the component $\kappa _{0\theta }$ has contributed after the Ansatz implementation.

From the set of equations (28)–(30), we can observe that, for fixed $s$ and considering the solutions for $n>0$, the correspondent solutions for $n<0$ can be attained by doing $g\rightarrow g~,\ a\rightarrow -a,~A_{0}\rightarrow -A_{0}$ and $( k_{\mathrm{AF}}) _{\theta } \rightarrow -( k_{\mathrm{AF}}) _{\theta }$. We can also note that, for $n$ and $( k_{\mathrm{AF}}) _{\theta }$ fixed, under the change $s\rightarrow -s$, the new solutions can be obtained by doing $g\rightarrow g, a\rightarrow a,~A_{0}\rightarrow -A_{0}$. By setting $( k_{\mathrm{AF}}) _{\theta }=0$, we recover the solutions of the MCSH model with $s$ playing the role of the Chern–Simons parameter.

Using the BPS equations (28)–(29) and the Gauss law (30), we rewrite the BPS energy density (20) as a sum of quadratic terms

$$\begin{aligned} \mathcal {E}_{\mathrm{BPS}}=B^{2}+2v^{2}(g^{\prime }) ^{2}+{2}e^{2} v^{2}({g}A_{0}) ^{2}+( A_{0}^{\prime })^{2}, \end{aligned}$$

(31)

showing that it is a positive-definite quantity for all values of $s$ and ${( k_{\mathrm{AF}}) _{\theta }}$.

3.1 Analysis of the boundary conditions

We begin discussing the behavior of the solutions of Eqs. (28–30) when $r\rightarrow 0$. As we are looking for well-behaved solutions, they are expanded in power series around the boundary conditions (25),

$$\begin{aligned} g(r)&= \sum _{j=1}^{\infty }g_{k}r^{k},~\end{aligned}$$

(32)

$$\begin{aligned} a(r)&= n-\sum _{j=1}^{\infty }a_{k}r^{k},~\end{aligned}$$

(33)

$$\begin{aligned} A_{0}(r)&= \omega _{0}-\sum _{j=1}^{\infty }A_{0}^{( k)}r^{k}, \end{aligned}$$

(34)

where $\omega _{0}=A_{0}(0)$ is a finite constant. As happens in the usual MCSH vortex configurations, $\omega _{{0}}$ depends on the boundary conditions above and it is numerically determined. By substituting the above series in Eqs. (28)–(30), one obtains the relevant first terms

$$\begin{aligned}&g(r) =G_{n}r^{n}-\frac{G_{n}e( ev^{2}+{{\omega _{{0}}} }s) }{4}r^{n+2}\nonumber \\&\mp \frac{G_{n}e\omega _{0}s{(k_{\mathrm{AF}})_{\theta }}}{18} r^{n+3}+{\mathcal {\cdots }}\end{aligned}$$

(35)

$$\begin{aligned}&a(r) =n-\frac{e(ev^{2}+{{\omega _{{0}}}}s) }{2}r^{2}\nonumber \\&\mp \frac{e\omega _{0}s{( k_{\mathrm{AF}}) _{\theta }}}{6}r^{3} +{\mathcal {\cdots }}\end{aligned}$$

(36)

$$\begin{aligned}&A_{0}(r) =\omega _{0}\pm \frac{{\omega _{{0}}( k_{\mathrm{AF}}) _{\theta }}}{2}r\nonumber \\&+\frac{4s(ev^{2}+{{\omega _{{0}}}}s) +3[ {( k_{\mathrm{AF}}) _{\theta }}] ^{2}\omega _{0}}{16}r^{2}+{\mathcal {\cdots }}. \end{aligned}$$

(37)

The first two equations confirm the boundary conditions imposed in (25), while the last one allows one to impose the following condition on the field $A_{0}$ at the origin:

$$\begin{aligned} A_{0}^{\prime }(0) =\pm \frac{{\omega _{{0}}( k_{\mathrm{AF}}) _{\theta }}}{2}. \end{aligned}$$

(38)

In order to find solutions satisfying the boundary conditions (26), we require that they obey a similar behavior to the Abrikosov–Nielsen–Olesen’s ones at $r\rightarrow \infty$, that is,

$$\begin{aligned} 1-g(r)&\sim r^{-1/2}e^{-\beta r},\nonumber \\ a(r)&\sim r^{1/2}e^{-\beta r},\\ A_{0}(r)&\sim r^{-1/2}e^{-\beta r},\nonumber \end{aligned}$$

(39)

where $\beta$ is a positive real number. By substituting them in Eqs. (28)–(30), it is shown that such a system can be consistently solved if

$$\begin{aligned} \beta _{\pm }&= \frac{1}{2}\sqrt{( \kappa _{\pm }) ^{2}+8e^{2} v^{2}\ }-\frac{\kappa _{\pm }}{2}, \end{aligned}$$

(40)

$$\begin{aligned} \kappa _{\pm }&= \sqrt{s^{2}+\frac{[ {( k_{\mathrm{AF}}) _{\theta } }] ^{2}}{4}}\pm \frac{{( k_{\mathrm{AF}}) _{\theta }}}{2}, \end{aligned}$$

(41)

with the sign $+(-)$ standing for $n>0$ $(n<0)$. It confirms the boundary conditions (26) for the fields $g$, $a,$ and it also provides the boundary condition at $r\rightarrow \infty$ for the field $A_{0}$:

$$\begin{aligned} A_{0}(\infty ) =0. \end{aligned}$$

(42)

We observe that for fixed $s$ and ${n>0}$, the $\beta _{+}$ parameter takes higher values if ${( k_{\mathrm{AF}}) _{\theta }}<0.$ We can consider two limit values,

$$\begin{aligned} \lim _{{( k_{\mathrm{AF}}) _{\theta }\rightarrow -\infty }}\beta _{+} =ev\sqrt{2},\quad \lim _{{(k_{\mathrm{AF}}) _{\theta }\rightarrow +\infty } }\beta _{+}=0, \end{aligned}$$

(43)

between which the parameter $\beta _{+}$ varies continually. It allows one to affirm the profiles with $( k_{\mathrm{AF}}) _{\theta }<0$ converge more quickly for their saturation values than those with $( k_{\mathrm{AF}}) _{\theta }>0$. For $( k_{\mathrm{AF}}) _{\theta }=0$ and fixed $s$, the behavior of $\beta$ is similar to the one of the BPS vortices coming from the MCSH model.

3.2 Numerical solutions

We now introduce the dimensionless variable $\rho =evr$ and implement the following changes in the fields:

$$\begin{aligned} g(r) \rightarrow \bar{g}( \rho ),\ a( r) \rightarrow \bar{a}( {\rho }) ,~A_{0}(r) \rightarrow v\bar{\omega }(\rho ),\\ \end{aligned}$$

$$\begin{aligned} B(r)\rightarrow ev^{2}\bar{B}(\rho ),~\mathcal {E}(r)\rightarrow v^{2}\bar{\mathcal {E}}(\rho ); \end{aligned}$$

and rescaling the LV coefficients

$$\begin{aligned} ( k_{\mathrm{AF}}) _{\theta }\rightarrow ev\lambda ,~s\rightarrow ev\bar{s}, \end{aligned}$$

(44)

where now $\lambda$ represents the $(1+2)$-dimensional CFJ parameter. Thereby, the expressions (28)–(30) are written in dimensionless form as

$$\begin{aligned} \bar{g}^{\prime } =\pm \frac{\bar{a}\bar{g}}{\rho }, \end{aligned}$$

(45)

$$\begin{aligned} \bar{B} =-\frac{\bar{a}^{\prime }}{\rho }=\pm (1-g^{2}) +\bar{s}\bar{\omega }, \end{aligned}$$

(46)

$$\begin{aligned} \bar{\omega }^{\prime \prime }+\frac{\bar{\omega }^{\prime }}{\rho }-\bar{s}\bar{B}\mp \lambda \left( \bar{\omega }^{\prime }+\frac{1}{2}\frac{\bar{\omega }}{\rho }\right) -2\bar{g}^{2}\bar{\omega }=0, \end{aligned}$$

(47)

while the dimensionless version of the BPS energy density is

$$\begin{aligned} \bar{\mathcal {E}}_{\mathrm{BPS}}=\bar{B}^{2}+2( {\bar{g}}^{\prime }) {^{2} }+{2\bar{g}^{2}\bar{\omega }}^{2}+( \bar{\omega }^{\prime }) ^{2}. \end{aligned}$$

(48)

We have performed the numerical analysis by considering three different values for the LV parameter, $\lambda =-1,0,+1,$ and for the winding numbers, $n=1,6,15$, while the Chern–Simons-like parameter is kept fixed, $\bar{s}=1.$ The value $\lambda =0$ reproduces the profiles of the MCSH vortices [9, 12, 13], which are depicted by green lines. Blue lines denote the BPS solution with $\lambda =-1$ and red lines the ones for $\lambda =+1$. The winding number is specified in the following way: dotted lines $( n=1)$, dashed lines $(n=6) ,$ and solid lines $( n=15)$. The resultant profiles for the topological solutions are depicted in Figs. 1, 2, 3, 4, 5, 6, 7, 8. All legends are summarized in Fig. 1.

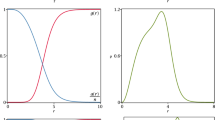
Figure 1 depicts the profiles of the Higgs field. For $n=1$ the profiles are very similar to the MCSH ones ($\lambda =0$ case), but they begin to differ from them for increasing values of the winding number. In general, the profiles with negative values of the CFJ parameter saturate more quickly than those with positive values, in accordance with Eq. (40).

Fig. 1

Scalar field $\bar{g}(\rho )$ (Blue lines for $\lambda =-1$, red lines for $\lambda =+1$, green lines for $\lambda =0$, represent the BPS solutions for the MCSH model)

Fig. 2

Vector potential $\bar{a}(\rho )$ (Blue lines for $\lambda =-1$, red lines for $\lambda =+1$, green lines for $\lambda =0$)

Figure 2 shows the profiles of the vector field.For $n=1$ the profiles are very similar to the MCSH ones ($\lambda =0$ case) but for $n>1,$ near the origin, the vector field magnitude can increase (for $\lambda =-1)$ or decrease (for $\lambda =1)$ in relation to the MCSH profiles. Near the origin, the first (second) behavior is associated a negative (positive) magnetic field, as is observed in Fig. 4. For $\rho \gg 0,$ the profiles always go to zero approaching the MCSH ones. Furthermore, for $\lambda =-1$ the vector field presents a region with increasing magnitude, which is compatible with a sharpened negative magnetic field around the origin. On the other hand, for $\lambda =+1$, the vector field decreases for increasing radius, providing a positive magnetic field which also engenders a sharpened structure around the origin.

Fig. 3

Scalar potential $\bar{\omega }(\rho )$ (Blue lines for $\lambda =-1$, red lines for $\lambda =+1$, green lines for $\lambda =0$. The small figure with dotted lines shows the solutions for $n=1$)

Fig. 4

Magnetic field $\bar{B}(\rho )$ (Blue lines for $\lambda =-1$, red lines for $\lambda =+1$, green lines for $\lambda =0$)

Fig. 5

The radius $\rho ^{*}$ as a function of the winding number $n$. For $\lambda =-1$, the magnetic flux inversion occurs for $n\ge 3$

Fig. 6

Magnetic field at origin, $\bar{B}(0)$, as a function of the winding number $n$. Blue dots for $\lambda =-1$, green dots for $\lambda =0$, and red dots for $\lambda =1$

Fig. 7

Electric field $\bar{\omega }^{\prime }(\rho )$ (Blue lines for $\lambda =-1$, red lines for $\lambda =+1$, green lines for $\lambda =0$)

Fig. 8

BPS energy density $\bar{\mathcal {E}}_{_{BPS}}(\rho )$ (blue lines for $\lambda =-1$, red lines for $\lambda =+1$, green lines for $\lambda =0$)

The scalar potential profiles, as appearing in Fig. 3, are negative throughout the radial axis, for all values of $n$ and $\lambda$. Near the origin, for all $n\ge 1$, the LV profiles are different from the usual MCSH solutions, with amplitudes increasing with negative $\lambda$. On the other hand, far from the origin, the LV profiles closely follow the behavior of the MCSH solutions (green lines). Near the origin, for $\lambda =-1,$ the LV profiles present an inverted pronounced form whose amplitude saturates at $\bar{\omega }(0)=-2.017$ (for $n\gg 1);$ for $\lambda =1,$ the profiles display a conical-shaped profile whose amplitude saturates as $\bar{\omega }(0)=-0.446$. Note that both solutions deviate significantly from the MCSH $(\lambda =0)$ value at the origin, $\bar{\omega }(0)=-1.0$. It is clear that the profile with $\lambda =-1$ decays faster than the one with $\lambda =1,$ as expected.

The magnetic field behavior is represented in Fig. 4. For $n=1$ (and different $\lambda$ values) it is very similar to the MCSH one, except near the origin, where the amplitude increases with $\lambda$ (see insertion with dotted lines in Fig. 4). Already, for $n>1,$ the magnetic profiles display two localized structures that define two well-defined domains: the first one is a pronounced magnitude flux region centered at the origin, which can be positive or negative depending on the sign of $\lambda$; the second one is a lump-like region whose maximum is located in an intermediary radial distance, being compatible with a ring-like magnetic field configuration (typical of the MCSH model) whose radius increases with $n$.

The magnetic field changes strongly in accordance with the sign of $\lambda$. Thus, for $\lambda \ge 0$, it is always positive. On the other hand, for $\lambda <0$, there are two possible behaviors: it is always positive or it can undergo reversion. In fact, there exists an $n_{0}$ such that it is positive for $n<n_{0}$ and changes sign for $n\ge n_{0}$ (there occurs a magnetic field flux inversion). In this last case, there is a radius $\rho ^{*}$ where $\bar{B}(\rho ^{*})=0$, with the magnetic field being negative between $0\le \rho <\rho ^{*},$ and being positive for $\rho >\rho ^{*}$.

For $\lambda =-1$, the dependence of $\rho ^{*}$ in terms of the winding number $n$ is depicted in Fig. 5, revealing an approximately linear behavior for large values of $n$.

Moreover, for $\lambda =-1$, $n_{0}=3$, the graph of Fig. 6 shows the value of $n$ for which the magnetic field is reversed. This inversion takes place for $n\ge 3$. Note that its value at the origin saturates at $\bar{B}(0)=-1.017$. Further, for $n>1$ and $\lambda =1$ the profiles are always positive, varying from the strong flux region centered at the origin to the ring-like region existing for an intermediary radial coordinate. For $\lambda =1$ and $n\gg 1$ the magnetic field at origin saturates at $\bar{B}(0)=0.553$. Despite this complex scenario, the total magnetic flux is positive and proportional to $n$, regardless the $\lambda$ value.

Note that the magnetic field reversion occurring in this LV scenario is a straightforward consequence of the richer structure of the associated differential equations. The magnetic field (29) is given by the same expression as the one that describes the magnetic field in the pure MCS-Higgs model. The difference comes from the behavior of the scalar potential, now governed by the modified Gauss law, Eq. (30), which presents an additional term in relation to the one of the MCSH model $(( k_{\mathrm{AF}}) _{\theta }=0)$ given by

$$\begin{aligned} A_{0}^{\prime \prime }+\frac{A_{0}^{\prime }}{r}-sB-2e^{2} v^{2}g^{2}A_{0}=0. \end{aligned}$$

(49)

From (29), the magnetic field could become negative (near the origin) only when $\vert sA_{0}\vert >\vert ev^{2}( 1-g^{2})\vert \simeq ev^{2},$ due to $g\simeq 0$ when $r\rightarrow 0$. For the values of the LV parameters here considered, Fig. 3 shows explicitly that in the MCSH case $( \lambda =0)$ this condition is never fulfilled. In fact, numerical simulations show $\vert sA_{0}\vert \le ev^{2}$ close to the origin (for all values of $n)$, so that in the MCSH case the magnetic field is nonnegative. For $\lambda =+1$, numerical simulations also show $\vert sA_{0}\vert <ev^{2}$ for all values of $n$, implying a nonnegative the magnetic field as well. On the other hand, for $\lambda =-1,~n\ge 3$, one observes that $\vert sA_{0}\vert >ev^{2}$ near the origin, and the magnetic field becomes negative. Moreover, for sufficiently large values of $r$, for all values of $\lambda$ and $n>0$, the condition $\vert sA_{0}\vert <\vert ev^{2}( 1-g^{2}) \vert$ is always satisfied, yielding a nonnegative magnetic field far from the origin whose profiles behave like the ones of the MCSH model.

Figure 7 contains the electric field profiles. Even for $n=1,$ these profiles are quite different in the neighborhood of the origin, where $\bar{\omega }^{\prime }(0)>0$ for $\lambda =-1$, $\bar{\omega }^{\prime }(0)=0$ for $\lambda =0,$ and $\bar{\omega }^{\prime }(0)<0$ for $\lambda =1$, changing a little for intermediary radius, and becoming very similar to the MCSH ones only far from the origin (see the insertion with dotted curves in Fig. 7). For $n>1,$ the electric field profiles display two localized significant structures, similarly to the magnetic field behavior. In the case $\lambda =-1$, the profiles are always positive, and there is a narrow cone centered at origin, whose amplitude saturates as $\bar{\omega }^{\prime }(0)=$ $1.008$ $( \text {for }n\gg 1)$, and a positive lump-like region localized in an intermediary radial coordinate. On the other hand, for $\lambda =+1$, the electric field becomes negative near the origin, yielding an inverted cone with smaller amplitude, which saturates as $\bar{\omega }^{\prime }(0)=$ $-0.223$ for $n\gg 1$. Further, as one goes away from the origin, the electric field changes its sign, becomes positive forming a ring-like structure around the origin, and vanishes for $\rho \rightarrow \infty$. Note that the LV electric solutions, similarly to the magnetic ones, differ from the usual MCSH ones mainly due the behavior near the origin: while the MCSH solutions are null at this point, the LV parameter may induce positive or negative electric fields in the origin neighborhood. This pattern is shared by the BPS energy density profiles.

The BPS energy density profiles are shown in Fig. 8. For $n=1$, the profiles are lumps centered at the origin with differing amplitudes, which overlap with each other far from $\rho =0$ (see the insertion with dotted curves in Fig. 8). When $n\gg 1$ and $\lambda =\pm 1$, the BPS energy density profiles present two well-pronounced regions, in accordance with the profiles of the magnetic and electric fields. The first one is a peak centered at the origin whose amplitude saturates at $0.356$ $(\text {for }\lambda =+1)$ and at $2.052$ $(\text {for }\lambda =-1)$. This concentration of energy at the origin is not present in the MCSH model. The second one is a lump-shaped region located at an intermediary distance from the origin, whose radius increases with $n,$ as happens in the MCSH model. For sufficiently large values of $n,$ the ring radius follows the inequality: $\rho _{\lambda =-1}\lesssim \rho _{\lambda =1}\lesssim \rho _{\lambda =0}$.

The concentration of energy around the origin for large values of $n$, depicted in Fig. 8, has no analog in the MCSH model although both models have the same expression for BPS energy density (see Eq. (31) or Eq. (48)):

$$\begin{aligned} \bar{\mathcal {E}}_{\mathrm{BPS}}=\bar{B}^{2}+2\left( {\bar{g}}^{\prime }\right) {^{2} }+{2\bar{g}^{2}\bar{\omega }}^{2}+( \bar{\omega }^{\prime }) ^{2}. \end{aligned}$$

(50)

Indeed, near the origin the third term is negligible. The other three terms have appreciable contributions at the origin only for $n=1$ (for all values of $\lambda )$. However, for $n>1,$ only the first and last terms contribute and the energy density becomes simply $\bar{\mathcal {E}} _{BPS}=\bar{B}^{2}+( \bar{\omega }^{\prime }) ^{2}.$ In the MCSH model the electric field at origin is null $\bar{\omega }^{\prime } (0)=0$ and $\bar{B}(0)\rightarrow 0$ for increasing values of $n$. This way, the MCSH energy density around the origin goes to zero when $n$ increases its value. On the other hand, in this Lorentz-violating model, both the electric field, $\bar{\omega }^{\prime }(0)=\lambda \bar{\omega }_{0}/2,$ and the magnetic field, $\bar{B}(0)=1+\bar{\omega }_{0},$ are nonzero at the origin for the analyzed values of $\lambda$ ($\lambda =\pm 1$, $\bar{\omega }_{0} <0$ and $\bar{\omega }_{0}\ne -1$). Under these considerations the BPS energy density becomes nonzero at the origin, $\bar{\mathcal {E}} _{\mathrm{BPS}}( 0) =( 1+{\bar{\omega }}_{0}) ^{2}+( {\bar{\omega }}_{0}) ^{2}/4$.

Therefore, we can conclude that both the inversion of the magnetic field and the concentration of the energy around the origin have a common origin: the new behavior of the scalar potential due to the presence of LV parameter $( k_{\mathrm{AF}}) _{\theta }$ in the Gauss law (30). Such a LV term enriches the vortex solutions obtained from the self-dual equations (28)–(29).

4 Conclusions and remarks

In this work, we have considered a Lorentz-violating planar electrodynamics, attained from the dimensional reduction of the Maxwell–Carroll–Field–Jackiw–Higgs model, as a theoretical environment for studying charged BPS vortex configurations. After writing the stationary equations of motion and the energy density, the axially symmetric usual vortex Ansatz was implemented, keeping only one Lorentz-violating parameter in the equations of the system. By manipulating the energy density, the BPS equations were obtained, confirming the existence of BPS solutions for such a model. The BPS energy remains connected with the magnetic flux quantization, as is usual.

The numerical simulations were performed for different values of the Lorentz-violating parameter, and distinct winding numbers. For $n=1$, at the origin, the solutions sometimes present notable deviations from the MCSH profiles. However, for large radius they closely follow the behavior of the MCSH ones. In general, the deviation is more accentuated for increasing winding number values. For $n>1$, the LV profiles keep some similarity to the usual MCSH solutions in the large radius region but decay in accordance with its respective mass scale: $\beta _{\lambda <0}>\beta _{\lambda =0}>\beta _{\lambda >0}$. The role played by the LV parameter becomes more pronounced at the origin, where it generates a peaked profile (absent in the MCSH solutions) in the magnetic/electric field and the energy density profiles. When $\lambda <0$ the magnetic field assumes negative values near the origin. However, for a sufficiently large radius, it flips its sign, providing two regions with opposite magnetic flux. The flipping of the magnetic flux represents a remarkable feature induced by Lorentz-violation, which may find applications in condensed matter systems endowed with magnetic flux reversion [29–32]. This feature was also observed in charged vortex configurations defined in the context of the CPT-even and nonbirefringent Lorentz-violating model of Ref. [78].

The analysis performed above can be extended for all values of $\bar{s}$ and $\lambda$. For $n>0$, a fixed $\bar{s}$, and $\lambda >0,$ there are always two well-defined regions with positive magnetic flux, occurring no magnetic field reversion. On the other hand, for fixed $\bar{s}$ and $\lambda <0,$ there always exists a sufficiently large winding number $n_{0}$ such that for $n>n_{0}$ the magnetic field reverses its sign. Consequently, there are always two well-defined regions with opposite magnetic flux. A similar result is obtained for $n<0$. However, in all cases the total magnetic flux remains quantized and proportional to the winding number.