1 Introduction

Accurate knowledge of the parton distribution functions (PDFs) of the proton is required for precision physics at the LHC. PDF sets are now available as determined by several groups [1–6] at leading-order (LO), next-to-leading-order (NLO) and next-to-next-to-leading-order (NNLO) accuracy in QCD. To obtain the cross-section predictions, the PDF sets should be paired with calculations of the coefficient functions at the matching order of the accuracy. Theoretical uncertainties for the predictions arise from both the PDF and the coefficient-function uncertainties.

Most of the Standard Model processes at the LHC are calculated to NLO accuracy. The uncertainties due to missing higher orders for the coefficient functions are typically determined by varying factorisation and renormalisation scales. This leads to large uncertainties often as large as \(10~\%\) of predicted cross sections, which usually exceed uncertainties due to the PDFs determination. For a handful of processes known at NNLO, the PDF uncertainties often exceed uncertainties due to missing higher orders in coefficient-function calculations.

The experimental precision achieved by the LHC experiments often exceeds the precision of theoretical calculations. Ultimately a more complete set of NNLO calculations should remedy the situation in future. At present, special methods are employed to reduce theoretical uncertainties. One such method is to measure ratios of observables which are expected to have similar higher-order corrections. For example, the \(W\) boson charge-asymmetry measurements [7, 8] employ almost full cancellation of the scale uncertainties for \(W^+\) compared to \(W^-\) production. However, this cancellation is not always possible. For example, the measurement of the \(WW\) di-boson to \(Z\) boson production cross-section ratio performed by the CMS collaboration using \(\sqrt{s}=7\) TeV data [9] benefits from cancellation of the PDF uncertainties, but the scale uncertainties for the NLO calculation dominate the theoretical uncertainty. While there is no complete NNLO calculation of the \(WW\) production available at presentFootnote 1, a reduction of the scale uncertainty for this ratio could be achieved by using NNLO calculations for the \(Z\) boson production cross section. To benefit from cancellation of the PDF uncertainties, correlated sets at NLO and NNLO are required in this case.

Several Monte Carlo (MC) simulation programs such as Powheg [10], MC@NLO [11] and aMC@NLO [12] use NLO matrix-element calculations which are matched to parton showers. The parton-shower simulations are limited to leading-log accuracy at the moment requiring LO PDFs for consistency. Coherently determined, correlated LO and NLO PDF sets may be exploited for the determination of PDF uncertainties for the experimental processes which are sensitive to the interplay of the hard-scattering matrix elements, soft resummation and PDF content of the proton. An example of such process is the \(W\) boson mass measurement using the charged-lepton transverse-momentum distribution from the \(W^{\pm } \rightarrow \ell ^{\pm } \nu \) decay.

This paper reports a determination of the PDFs with correlated uncertainties for LO, NLO and NNLO sets. The sets are determined using the data from the HERA experiments [5] and the HERAFitter analysis framework [5, 13, 14]. The experimental uncertainties are estimated using the MC method [15] and then transformed to eigenvector PDF sets [16, 17]. The new PDF sets are used to study correlations of the \(Z\) boson production cross section calculated at NLO and NNLO and to determine theoretical uncertainties for the \(WW\) di-boson over \(Z\) boson production cross-section ratio. An overall reduction of the theoretical uncertainty is observed.

2 PDF analysis

The PDF analysis reported in this paper uses the combined HERA data [5]. These input data are accurate measurements of the inclusive deep-inelastic scattering (DIS) neutral- and charged-current cross sections combined by the H1 and ZEUS collaborations. The neutral-current data cover a wide range in Bjorken \(x\) and absolute four-momentum transfer squared, \(Q^2\), sufficient to cover the LHC kinematics, while the charged-current data provide information to disentangle contributions from \(u\)-type and \(d\)-type quarks and anti-quarks at \(x>0.01\).

This analysis is based on the open-source QCD fit framework as implemented in the HERAFitter program using the QCDNUM evolution code [18] for DGLAP evolution at LO, NLO and NNLO [19–24]. To compute DIS cross sections, the light-quark coefficient functions are calculated using QCDNUM in the \(\overline{MS}\) scheme [25] with the renormalisation and factorisation scales set to \(Q^2\).

The heavy quarks are dynamically generated and the heavy-quark coefficient functions for the neutral-current \(\gamma ^*\) exchange process are calculated in the general-mass variable-flavour-number scheme (VFNS) of [26–28] with up to five active quark flavours. For the charged-current process, pure \(Z\) exchange and \(\gamma ^*/Z\) interference contributions to the neutral-current process, the heavy quarks are treated as massless. The NLO QCD analysis of the combined \(F_2^{cc}\) data, performed by the H1 and ZEUS collaborations [29], demonstrated that the preferred value of the charm-quark-mass parameter, \(M_c\), used in VFNS (related to the charm-quark pole mass) is strongly scheme dependent. This analysis is repeated here to determine the preferred value for the NNLO heavy-quark coefficient functions. As a cross check, an NLO analysis is repeated first and found to reproduce the H1 and ZEUS results. The preferred mass-parameter value at NLO (NNLO) is \(M_c = 1.38\) GeV (\(M_c = 1.32\) GeV) and it is used for the results reported in this paper. For the LO fit, the charm mass is set to \(M_c = 1.38\) GeV. The bottom-quark-mass parameter is set to \(4.75\) GeV for fits at all orders.

The strong coupling constant is set at the \(Z\) boson mass \(M_Z\) to \(\alpha _S(M_Z) = 0.1184\) [30] for both NLO and NNLO fits. The LO fit uses \(\alpha _S(M_Z)=0.130\), similar to the values used in CTEQ6L [31], HERAPDF1.5LO [32], MSTW08LO [3] and NNPDF2.1LO [33] PDF sets.

The data included in the fit are required to satisfy the \(Q^2>Q^2_\mathrm{min}=7.5\) GeV\(^2\) condition in order to stay in the kinematic domain where perturbative QCD calculations can be applied. Variations of these choices are considered as model PDF uncertainties.

The PDFs for the gluon and quark densities are parameterised at the input scale \(Q^2_0=1.7\) GeV\(^2\) as follows:

$$\begin{aligned}&xg(x) = A_g x^{B_g} (1-x)^{C_g} - A'_g x^{B'_g} (1-x)^{C'_g}; \end{aligned}$$
(1)
$$\begin{aligned}&x\bar{U}(x) = A_{\bar{U}} x^{B_{\bar{U}}}(1-x)^{C_{\bar{U}}}(1 + D_{\bar{U}}x + E_{\bar{U}}x^2); \end{aligned}$$
(2)
$$\begin{aligned}&x\bar{D}(x) = A_{\bar{D}} x^{B_{\bar{D}}}(1-x)^{C_{\bar{D}}}; \end{aligned}$$
(3)
$$\begin{aligned}&x u_v(x) = A_{u_v} x^{B_{u_v}}(1-x)^{C_{u_v}}(1 + E_{u_v}x^2); \end{aligned}$$
(4)
$$\begin{aligned}&x d_v(x) = A_{d_v} x^{B_{d_v}}(1-x)^{C_{d_v}}(1 + D_{d_v}x). \end{aligned}$$
(5)

Here the decomposition of the quark densities follows the one from [14] with \(x\bar{U}(x) = x\bar{u}(x)\) and \(x\bar{D}(x) = x\bar{d}(x) + x\bar{s}(x)\). The contribution of the \(s\)-quark density is coupled to the \(d\)-quark density as \(x\bar{s}(x) = r_s x\bar{d}(x)\) with \(r_s=1.0\), for fits at all orders, as suggested by [34], and \(x\bar{s}(x) = x s(x)\) is assumed. The extra polynomial parameters \(D_{d_v}, D_{\bar{U}}, E_{\bar{U}}\) are set to zero for the central fit; however, they are allowed to vary to estimate the parameterisation uncertainty. The normalisation of the \(x u_v\) (\(x d_v\)) valence-quark density, \(A_{u_v}\) (\(A_{d_v}\)), is given by the quark-counting sum rule. The normalisation of the gluon density, \(A_g\), is determined by the momentum sum rule. The \(x\rightarrow 0\) behaviour of the \(u\)- and \(d\)-sea-quark density is assumed to be the same leading to two additional constraints \(B_{\bar{U}} = B_{\bar{D}}\) and \(A_{\bar{U}} = A_{\bar{D}}/(1 + r_s)\). The negative term for the gluon density is suppressed at high \(x\) by setting \(C'_g = 25\). After application of these constraints, the central fit has \(13\) free parameters.

The fit uses the \(\chi ^2\) definition from [5] with an additional penalty term described in [35]. The statistical uncertainties use expected instead of observed number of events. The data contain \(114\) correlated systematic uncertainty sources as well as bin-to-bin uncorrelated systematic uncertainties. All systematic uncertainties are treated as multiplicative. The minimisation with respect to the correlated systematic uncertainty sources is performed analytically while the minimisation with respect to PDF parameters uses the MINUIT program [36]. The central fit result is comparable to the HERAPDF1.0 set [5]. The \(\chi ^2\) per degree of freedom values, \(\chi ^2/N_\mathrm{dof}\), for the LO, NLO and NNLO fits are \(523/537\), \(500/537\) and \(498/537\), respectively.

The PDF uncertainties arising from the experimental uncertainties are estimated using the MC method [15]. The method consists in preparing a number of \(N_r\) replicas of the data by fluctuating the central values of the cross sections randomly within their statistical and systematic uncertainties taking into account correlations. The uncorrelated and correlated experimental uncertainties are assumed to follow the Gaussian distribution. A set of \(1500\) replicas is prepared and used as input for the LO, NLO and NNLO QCD fit. The fits are inspected to ensure that the minimisation has converged for fits at all three orders. Replicas where one of the fits has failed are discarded. To check that this procedure does not introduce any bias, a study in which the non-converged fits are included has been performed. It is found that the non-converged fits have negligible impact. A total of \(N_r = 1337\) replicas remain for which fits at all orders have converged and they are used for the further analysis.

A test of the fit results is done by investigating the \(\chi ^2\) distribution. For the MC method, the \(\chi ^2\) distribution is expected to have a mean value of \(2 N_\mathrm{dof}\) since it is given by the combination of fluctuations in the data plus random fluctuations for each MC replica. Figure 1a shows the observed \(\chi ^2\) distributions for the fits at LO, NLO and NNLO. The distributions follow the expected \(\chi ^2\) distribution. Figure 1b shows the correlation of the \(\chi ^2/N_\mathrm{dof}\) values for the fits at NLO and NNLO. A high degree of correlation is observed.

Fig. 1
figure 1

Distribution of \(\chi ^2/N_\mathrm{dof}\) for fits to \(1337\) data replicas at LO, NLO and NNLO (a). Correlation of \(\chi ^2/N_\mathrm{dof}\) between NLO and NNLO fits (b). The vertical line in a indicates the expected mean value of the \(\chi ^2\) distribution for the fits to the data replicas in the MC method (\(2\times N_\mathrm{dof}\))

Full size image

The central values, \(\mu \), and uncertainties, \(\Delta \), of the predictions, based on MC PDF sets, are estimated using the mean values and standard deviations over the predictions for each replica, \(\sigma _i\). The predictions can be cross sections calculated at different orders or PDFs determined at given \(x,Q^2\) values. The correlation due to experimental uncertainties between NLO and NNLO predictions is determined as

$$\begin{aligned}&\rho ^\mathrm{NLO-NNLO}= \frac{1}{N_r} \frac{ \sum ^{N_r}_{i=1} (\sigma _i^\mathrm{NLO}-\mu ^\mathrm{NLO} )(\sigma _i^\mathrm{NNLO} - \mu ^\mathrm{NNLO}) }{ \Delta ^\mathrm{NLO} \Delta ^\mathrm{NNLO}}. \end{aligned}$$

For many applications, the eigenvector representation of the PDF uncertainties [16, 17] is more convenient than the MC representation. The eigenvector representation typically requires fewer PDF sets to describe the PDF uncertainties. A procedure suggested in [37] is adapted here to determine the eigenvector representation for the correlated LO and NLO as well as NLO and NNLO MC PDF sets.

The procedure makes use of the ability of the QCDNUM program to perform PDF evolution based on a tabulated input. An \(x\)-grid of \(N_x = 97\) points \(x_l\) with variable spacingFootnote 2 is used to determine the \(N_f=5\) average PDFs \(x\overline{f(x_l)}\). The PDFs are represented by Eqs. 1–5 including correlations between PDFs at the \(N_o=2\) orders, LO-NLO and NLO-NNLO. The correlated uncertainties are described by the dimension \(N=N_x \times N_f \times N_o = 97\times 5\times 2\) covariance matrix \(C\) which is represented as

$$\begin{aligned} C_{ij} = \sum _{k=1}^N V_{ik}V_{jk}, \end{aligned}$$

where the matrix \(V\) is built using eigenvectors of \(C\) times the square root of the corresponding eigenvalues. For each vector \(V_k\), a symmetric PDF error set is defined at the starting scale as

$$\begin{aligned} x f^k(x_l) = x \overline{f(x_l)} + V_{ik}. \end{aligned}$$

Here the index \(i\) is determined by the \(x\)-grid index \(l\), PDF flavour index \(f\) and order index \(o\) as \(i = l + (f-1)N_x + (o-1)N_xN_f\). The resulting error sets are evolved from the starting scale to other scales using QCDNUM. Since the eigenvalues are found to be strongly ordered in magnitude, only \(39\) (\(45\)) eigenvectors corresponding to leading eigenvalues can approximate the matrix \(C\) for NLO-NNLO (LO-NLO) sets with high precision, as demonstrated in the following discussion.

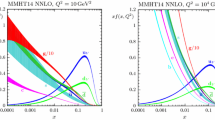
The NLO PDFs with their uncertainties determined using the MC method and its eigenvector representation, using \(39\) sets, are shown in Fig. 2. Very good agreement is observed between the two representations. A similar picture is observed for the LO and NNLO PDFs. The correlation among PDF values at different \(x\) is shown in Fig. 3. The eigenvector representation reproduces all the correlations very well with small deviations at high \(x\) (\(x>0.7\)). All PDFs show high degree of correlation for neighbouring \(x\) values which can be explained by intrinsic smoothness of the PDF parameterisation, which has few parameters, and the fact that the PDFs at comparable \(x\) are constrained by similar input data. There is a sizeable anti-correlation between PDFs at small and large \(x\) values caused by sum rules. The correlation patterns as a function of \(x\) are similar for PDFs determined at NLO and NNLO and, with the exception of the gluon density at high \(x\), there is a strong correlation between NLO and NNLO PDFs. A qualitatively similar, strong correlation is observed for the PDFs determined at LO and NLO; however, it is somewhat reduced compared to that for the NLO and NNLO PDFs. This explains why more eigenvectors are required for the correlated LO-NLO PDF set. As a cross check, the correlations between NLO and NNLO PDFs are studied using a bi-log-normal parameterisation

$$\begin{aligned} x f(x) =a x^{p - b\log (x)} (1-x)^{q-d \log (1-x)} \end{aligned}$$

instead of the parameterisation of  Eq. 1–5. Similar correlation patterns are observed with some differences for the gluon density at high \(x\), where the uncertainties are large.

Fig. 2
figure 2

NLO PDFs with the experimental uncertainty bands as well as the relative uncertainties determined by the MC method and its eigenvector representation. From top to bottom, the panels show \(xu_v(x)\), \(xd_v(x)\), \(x\bar{U}(x)\), \(x\bar{D}(x)\) and \(xg(x)\) distributions

Full size image
Fig. 3
figure 3

Correlation coefficients, given in percent and represented by different colours, among different PDFs at NLO and NNLO at the starting scale \(Q^2=1.7\) GeV\(^2\) and \(x\)-grid points. From top to bottom, the panels show correlation coefficients for the \(xu_v(x)\), \(xd_v(x)\), \(x\bar{U}(x)\), \(x\bar{D}(x)\) and \(xg(x)\) distributions. The left column corresponds to the original MC-method calculation and the right shows the result of the eigenvector representation. Each panel shows the correlation coefficients as a function of the \(x\)-grid point for the NLO (bins \(1-97\)) and NNLO (bins \(98-194\)) PDFs. Bins \(0\), \(27\), \(43\), \(62\), \(78\) and \(97\) correspond to anchor points at \(x=10^{-5}\), \(0.01\), \(0.1\), \(0.4\), \(0.7\) and \(1.0\) with logarithmic \(x\) spacing between them

Full size image

Model uncertainties in PDFs arise from the uncertainties of the input parameters of the fit. The value of the strange-quark density suppression \(r_s\) is varied by \(\pm 0.30\). The variation range is defined by the uncertainties found by the ATLAS collaboration [34, 38] and cover the somewhat lower value determined by the CMS collaboration [8, 39]. Based on the ATLAS analysis, this variation is considered to be fully correlated between the NLO and NNLO PDFs.

The uncertainties of the heavy-quark masses are also assumed to be fully correlated between NLO and NNLO. The charm-quark mass uncertainty is taken from the H1 and ZEUS analysis [29] to be \(0.06\) GeV. The bottom-quark mass is varied between \(4.3\) and \(5.0\) GeV.

The uncertainties of the QCD evolution at small \(Q^2\) are probed by varying the \(Q^2_\mathrm{min}\) cut between \(5\) and \(10\) GeV\(^2\). The choice of the \(Q^2_0\) value is also tested by varying down to \(Q^2_0 = 1.5\) GeV\(^2\). The resulting change in the PDFs is considered as a symmetric uncertainty.

The strong coupling constant at both NLO and NNLO, maybe considered to be the same, or different, following the analyses from [4, 5] or [1, 3], respectively. To cover different possibilities, \(\alpha _S(M_Z)\) is varied by \(\pm 0.002\) independently for the LO, NLO and NNLO fits.

Parameterisation uncertainties are estimated by including additional terms in the polynomial expansion following the procedure outlined in [5]. The extra terms are added coherently to LO, NLO and NNLO sets to preserve the correlation pattern.

The PDF sets are reported in the LHAPDF v6 format [40]. The correlated NLO-NNLO and LO-NLO sets are labelled as “HF14cor-nlo-nnlo” and “HF14cor-lo-nlo”, respectively. Separate sets are provided for experimental and model plus parameterisation (“HF14cor-lo-nlo-nnlo_VAR”) uncertainties. The experimental uncertainties are reported as both Monte Carlo (“HF14cor-lo-nlo-nnlo_MC”) and symmetric eigenvector (“HF14cor-nlo-nnlo_EIGSYM”, ”HF14cor-lo-nlo_EIGSYM”) sets. The symmetric eigenvector set is ordered according to the size of the PDF uncertainty, approximate calculations may use the first \(26\) sets only. The reference set for all PDF sets is chosen to be the set averaged over the MC replicas.

3 Prediction of \(Z\) and \(WW\) production cross sections at the LHC

The usage of the correlated NLO and NNLO PDF sets is exemplified by calculating \(WW\) di-boson and \(Z\) boson production cross sections for the \(pp\) collisions at a \(\sqrt{s}=7\) TeV centre-of-mass energy. The recent measurements of \(WW\) di-boson production by the ATLAS and CMS collaborations [9, 41] have generated considerable interest from the theoretical community. The uncertainties of the measurements and predictions are comparable and the measurements are about \(1-2\sigma \) above the expectations. The difference may originate from missing higher orders [42, 43], electroweak effects [44] and possible New Physics contributions [45].

The \(WW\) di-boson and \(Z\) boson production processes are expected to have similar PDF dependences which may lead to reduced uncertainties for the ratio of the cross sections. In the following discussion, the predictions obtained using the HF14cor-nlo-nnlo PDF sets are compared to the measurement of the ratio obtained by the CMS collaboration [9].

The total cross section for \(W^+W^-\) di-boson production, \(\sigma _{WW}\) (called \(WW\) di-boson production in the following) is calculated at NLO using the MCFM v6.6 program [46, 47]. The calculation includes the gluon–gluon initiated box diagram which first contributes at order \(\alpha ^2_S\) and so is formally NNLO. The factorisation and renormalisation scales are given by half of the scalar sum of the transverse momenta of the outgoing final-state particles, \(H_T/2\). The contribution from Higgs boson production, which contributes approximately two percent, is not included. As a cross check, the total \(WW\) di-boson cross-section predictions from the original paper [47] are reproduced using the corresponding setup.

The total cross section for \(Z/\gamma ^*\) boson production, \(\sigma _Z\) (referred to as \(Z\) boson production in the following discussion) is calculated at NLO and NNLO using FEWZ [48, 49]. The invariant mass for the lepton pair is chosen to be \(60<M_{\ell \ell }<120\) GeV as in the analysis of the CMS collaboration. The factorisation and renormalisation scales are fixed to the \(Z\) boson pole mass, \(M_Z\). The FEWZ calculation includes NLO electroweak corrections, which are small for this mass range. The contribution from \(\gamma \gamma \rightarrow \ell \ell \) processes is not included for either \(WW\) di-boson or \(Z\) boson production.

Uncertainties due to missing higher-order corrections are estimated by varying the default scale up and down by a factor of two, for both factorisation and renormalisation scales simultaneously or independently, excluding the variation in opposite directions. An envelope of all variations is built and maximal positive and negative deviations are taken as the asymmetric uncertainty. The scale uncertainty is dominated by the variation of the renormalisation scale for \(WW\) di-boson production and by the variation of the factorisation scale for \(Z\) boson production. The scale uncertainty is treated as uncorrelated between \(WW\) di-boson and \(Z\) boson production. The experimental PDF uncertainties are symmetric by construction. The model and parameterisation PDF uncertainties are quoted as asymmetric.

The resulting cross sections with their correlations are given in Table 1 and shown in Fig. 4. The predictions for \(Z\) boson production calculated at NLO and NNLO show a high degree of correlation. The scale uncertainties are reduced significantly for the NNLO prediction, becoming smaller than the PDF uncertainties. The central value of the prediction at NNLO is larger than that for NLO by \(1.7~\%\). This difference is smaller than the uncertainty of \(\sigma _Z^\mathrm{NLO}\) on the missing higher-order corrections, estimated by the scale variation.

Fig. 4
figure 4

Correlation of the cross-section predictions for \(Z\) boson production calculated at NLO and NNLO, \(WW\) di-boson and \(Z\) boson production both calculated at NLO and \(WW\) di-boson production calculated at NLO and \(Z\) boson production calculated at NNLO. The error bars indicate scale uncertainties

Full size image
Table 1 Cross-section predictions, experimental (Exp.) as well as model and parameterisation (Mod.) PDF uncertainties, scale uncertainties and correlation coefficients for the \(Z\) boson and \(WW\) di-boson production calculated at NLO and NNLO using the HF14cor-nlo-nnlo PDF set
Full size table

The correlation of the \(\sigma _{WW}\) and \(\sigma _Z\) cross sections is very large for the experimental PDF uncertainties for both the NLO and the NNLO calculations. Model and parameterisation PDF uncertainties are also highly correlated for most of the uncertainty sources when both cross sections are calculated at NLO. When \(\sigma _Z\) is calculated at NNLO, an anti-correlation for some sources is observed. A detailed breakdown of the model and parameterisation uncertainties for the total cross-section calculations is given in Table 2.

Table 2 Shifts of the \(WW\) di-boson and \(Z\) boson production cross sections due to the model and parameterisation variations in the PDF fit
Full size table

An anti-correlation between \(\sigma _{WW}\) and \(\sigma _Z\) is observed for the variation of the \(r_s\) parameter. In addition, an anti-correlation between \(\sigma ^\mathrm{NLO}_{Z}\) and \(\sigma ^\mathrm{NNLO}_{Z}\) is observed for the variation of the \(Q^2_\mathrm{min}\) cut as well from the addition of the \(D_{u_v}\) parameter to the PDF parameterisation. A positive correlation between \(\sigma _{WW}\) and \(\sigma _{Z}\) at both orders is observed for the \(M_c\), \(M_b\) and \(\alpha _S(M_Z)\) variations.

Effects of variations of the input parameters other than considered in Table 2 can be estimated by scaling the reported shifts assuming a linear dependence of the cross sections. Validity of this approach has been verified for the \(r_s\) parameter which has been varied down to \(r_s=0.3\) in steps of \(0.1\). The observed anti-correlation between \(\sigma _{WW}\) and \(\sigma _{Z}\) for the \(r_s\)-parameter variation can be caused in part by the different \(x\) ranges probed by the two processes and the assumption that the \(s\)-quark density has the same \(x\) dependence as the \(\bar{d}\)-quark density, adopted in this paper because of a lack of sensitivity of the HERA data. The effect of this assumption can be probed by treating the \(r_s\)-parameter variation as uncorrelated for the two cross sections. Note, however, that the anti-correlation leads to a conservative uncertainty for the \(\sigma _{WW}\) to \(\sigma _{Z}\) cross-section ratio.

The predicted ratio \(\sigma _{WW} / \sigma _Z\) using the \(Z\) boson production cross sections calculated at NLO and NNLO is given in Table 3. The predictions are compared to the CMS data in Fig. 5. The data and calculations agree reasonably well. The scale uncertainty is reduced by using \(\sigma ^\mathrm{NNLO}_Z\). Experimental PDF uncertainties cancel in the ratio becoming negligible compared to the scale uncertainties.

Fig. 5
figure 5

Ratio of the \(WW\) di-boson to \(Z\) boson production cross sections calculated at NLO and NLO/NNLO compared to the result obtained by the CMS collaboration (hatched area). The inner, middle and outer filled error bars of the predictions indicate experimental and full PDF uncertainties and the total uncertainty calculated as the scale and full PDF uncertainties added in quadrature, respectively

Full size image
Table 3 Predictions of the \(WW\) di-boson to \(Z\) boson production cross-section ratio with PDF and scale uncertainties
Full size table

A detailed breakdown of the model uncertainty sources for the ratio of the cross sections is given in Table 4. The \(r_s\) variation results in a large uncertainty for the ratio using both NLO and NNLO calculations of \(\sigma _Z\). Additional experimental input constraining \(r_s\) will allow this uncertainty to be reduced. Variations of the \(Q^2_\mathrm{min}\) cut and addition of the \(D_{u_v}\) parameter cancel in the ratio for \(\sigma ^\mathrm{NLO}_{WW}/\sigma ^\mathrm{NLO}_Z\); however, these variations have significant impact on \(\sigma ^\mathrm{NLO}_{WW}/\sigma ^\mathrm{NNLO}_Z\). The variations of \(M_c\), \(M_b\) and \(\alpha _S(M_Z)\) do not affect the ratio significantly for either the NLO or NNLO calculations of \(\sigma _Z\).

Table 4 Shifts of the ratios \(\sigma ^\mathrm{NLO}_{WW}/\sigma ^\mathrm{NLO}_{Z}\) and \(\sigma ^\mathrm{NLO}_{WW}/\sigma ^\mathrm{NNLO}_{Z}\) due to the model and parameterisation variations in the PDF fit
Full size table

An alternative approach to benefit from the partial cancellation of the PDF uncertainties is to use NNLO PDFs for the processes with only NLO matrix-element calculations. The mismatch of the calculation order is beyond the NLO accuracy and thus could be considered to be covered by the NLO calculation uncertainty, which is estimated by the scale variation. Given the observed anti-correlations between NLO and NNLO sets, this procedure may, however, lead to an underestimation of the PDF uncertainties. A calculation of the \(WW\) di-boson to \(Z\) boson production cross-section ratio using the HF14cor-nlo-nnlo NNLO PDF set yields

$$\begin{aligned} \begin{array}{l} \sigma _{WW}^\mathrm{NLO(NNLO\,PDF)}/\sigma _Z^\mathrm{NNLO} =\\ \quad [1.527\pm 0.008\,(\mathrm{exp.})^{+0.023}_{-0.022}\,(\mathrm{mod.})] \times 10^{-3}, \end{array} \end{aligned}$$

where the uncertainties represent the experimental (exp.) and model plus parameterisation (mod.) PDF errors only and are very similar to the PDF errors for the \(\sigma _{WW}^\mathrm{NLO}/\sigma _{Z}^\mathrm{NLO}\) ratio. The central value is consistent with the \(\sigma ^\mathrm{NLO}_{WW}/\sigma ^\mathrm{NNLO}_{Z}\) calculation within \(0.7~\%\); however, the PDF uncertainties may be underestimated by \(30\)–\(50\) %.

Adding the PDF and scale uncertainties (Table 4) in quadrature, the cross-section ratio of \(WW\) di-boson to \(Z\) boson production calculated as the ratio of NLO predictions is

$$\begin{aligned} \sigma _{WW}^\mathrm{NLO}/\sigma _Z^\mathrm{NLO} = [1.543^{+0.073}_{-0.062}] \times 10^{-3} \end{aligned}$$

and as the ratio of NLO to NNLO predictions is

$$\begin{aligned} \sigma _{WW}^\mathrm{NLO}/\sigma _Z^\mathrm{NNLO} = [1.517^{+0.051}_{-0.047}] \times 10^{-3} . \end{aligned}$$

The usage of the mixed-order calculations leads to a \(30\)–\(40\) % reduction of the overall theoretical uncertainty.

4 Summary

Sets of LO, NLO and NNLO parton distribution functions are reported preserving the correlations of PDFs determined at different orders. The sets are determined with the HERAFitter program using the combined HERA data. The input parameters of the fits use recent experimental results on the charm-quark mass parameter \(M_c\) and the strangeness suppression parameter \(r_s\). The experimental PDF uncertainties are determined using the MC method and reported using both MC and eigenvector representations. A high degree of correlation is observed for the PDFs at different perturbative order and similar Bjorken variable \(x\). The model and parameterisation PDF uncertainties are estimated by varying the values of the input parameters and by adding extra terms in the PDF parameterisation.

The correlated NLO and NNLO PDF sets are used to calculate the \(WW\) di-boson and \(Z\) boson production cross sections. The \(WW\) di-boson production cross section is calculated at NLO using MCFM. The \(Z\) boson production cross section is calculated at NLO and NNLO using FEWZ. Significant correlations of the PDF uncertainties are observed for the cross sections calculated at different orders. For the ratio of the \(WW\) di-boson to \(Z\) boson production cross sections an overall \(30\)–\(40\) % reduction of uncertainties is observed when using mixed-order calculations due to the reduced higher-order uncertainty for the \(Z\) boson production cross section calculated at NNLO.