Disentangling coherent and incoherent quasielastic $J/\psi$ photoproduction on nuclei by neutron tagging in ultraperipheral ion collisions at the LHC

Abstract

We consider $J/\psi$ photoproduction in ion–ion ultraperipheral collisions (UPCs) at the LHC and RHIC in the coherent and incoherent quasielastic channels with and without accompanying forward neutron emission and analyze the role of nuclear gluon shadowing at small $x$,  $x=10^{-4}{-}10^{-2}$, in these processes. We find that despite the good agreement between large nuclear gluon shadowing and the ALICE data in the coherent channel, in the incoherent channel, the leading twist approximation predicts the amount of nuclear suppression which is by approximately a factor of $1.5$ exceeds that seen in the data. We hypothesize that part of the discrepancy can be accounted for by the incoherent inelastic process of $J/\psi$ photoproduction with nucleon dissociation. To separate the high-photon-energy and low-photon-energy contributions to the $\mathrm{d}\sigma _{AA\rightarrow AAJ/\psi }(y)/\mathrm{d}y$ cross section, we consider ion–ion UPCs accompanied by neutron emission due to electromagnetic excitation of one or both colliding nuclei. We describe the corresponding PHENIX data and make predictions for the LHC kinematics. In addition, in the incoherent quasielastic case, we show that the separation between the low-photon-energy and high-photon-energy contributions can be efficiently performed by measuring the correlation between the directions of $J/\psi$ and the emitted neutrons.

1 Introduction

Recently coherent and incoherent photoproduction of $J/\psi$ in ultraperipheral collisions (UPCs) of nuclei was measured by the ALICE collaboration at the LHC [1, 2]. In the coherent channel, a large reduction of the coherent cross section—approximately by a factor of three—as compared to the impulse approximation has been reported. Such a magnitude of the suppression was found to be in the reasonable agreement with the expectations of the approaches predicting significant nuclear gluon shadowing at $x \approx 10^{-3}$ ($x$ is the fraction of the nucleus momentum carried by gluons), notably with predictions of the leading twist approach to nuclear shadowing [3, 4] and with the results of the EPS09 global QCD fit to nuclear parton distributions [5]. Thus, charmonium photoproduction on nuclear targets is a useful tool to study nuclear gluon shadowing at small $x$.

The aim of this paper is twofold. First, we extend application of the leading twist approach to nuclear shadowing [6] to incoherent quasielastic photoproduction of $J/\psi$ on nuclei and show that the suppression of both coherent and incoherent $J/\psi$ photoproduction in ion–ion UPCs can be described in the same framework. A comparison of the resulting theoretical prediction for the cross section of incoherent $J/\psi$ photoproduction in Pb–Pb UPCs at the LHC to the ALICE data, which is also characterized to correspond to an incoherent quasielastic process [1], shows that the expected suppression due to nuclear shadowing is larger than that seen in the data. We argue that this does not only place additional constraints on models of nuclear shadowing down to $x \approx 10^{-4}$ but also indicates that additional processes can contribute to the ALICE data. In particular, on top of incoherent $J/\psi$ photoproduction on nuclei resulting from the target nucleus excitation, the $\gamma +A \rightarrow J/\psi +Y+(A-1)^{*}$ process driven by the $\gamma +N \rightarrow J/\psi +Y$ nucleon dissociation ($Y$ denotes products of the nucleon dissociation) accompanied by the nucleus breakup into the $(A-1)^{*}$ system consisting of nucleus debris or nucleons also leads to the inelastic final state. The calculation of the $\gamma +A \rightarrow J/\psi +Y+(A-1)^{*}$ contribution is rather involved, reflecting different mechanisms of the elementary reaction at small and large $|t|$ considered in [7], and it will be addressed in a separate publication.

Second, we discuss specifics of and make predictions for coherent and incoherent charmonium production in nucleus–nucleus UPCs accompanied by forward neutron emission which can be studied at the LHC with the ALICE, CMS, and ATLAS detectors equipped by zero degree calorimeters (ZDC). The following channels can be studied: (i) one of the nuclei emits at least one neutron while its partner does not—(0nXn); (ii) both nuclei emit neutrons in opposite directions—(XnXn), (iii) neither of the nuclei emits neutrons—(0n0n). We show that selection of a specific channel can strongly influence the ratio of the cross sections of incoherent to coherent $J/\psi$ photoproduction in Pb–Pb UPCs at the LHC. In particular, we argue that the study of incoherent production of charmonium in ion–ion UPCs with the nucleus breakup allows one to separate the low-photon-energy and high-photon-energy contributions to nuclear $J/\psi$ photoproduction and, hence, to provide additional information on the dynamics of nuclear shadowing of the gluon distribution in nuclei which is complementary to that obtained from coherent onium production.

This paper is organized as follows. In Sect. 2, we discuss the suppression of the coherent and incoherent nuclear $J/\psi$ photoproduction cross sections due to nuclear shadowing. We briefly recapitulate main results of the vector meson dominance and the color dipole models for these processes and present the derivation of the coherent $\sigma _{\gamma A \rightarrow J/\psi A}$ and the incoherent $\sigma _{\gamma A \rightarrow J/\psi A^{\prime }}$ cross sections in the leading twist approximation. In Sect. 3, using the results of Sect. 2, we make predictions for the coherent and incoherent cross section of $J/\psi$ photoproduction in ion–ion UPCs without and with neutron emission and analyze the obtained results. Section 4 presents a brief summary of the obtained results.

2 Nuclear gluon shadowing in coherent and incoherent $J/\psi$ photoproduction on nuclei

2.1 The coherent nuclear $J/\psi$ photoproduction cross section

The earliest model for production of vector mesons off nuclei is the vector meson dominance model based on hadronic degrees of freedom [8]. In the high-energy optical limit of the Glauber model, the standard expression for the cross section of coherent $J/\psi$ photoproduction on a nuclear target reads (see, e.g., [9]):

$$\begin{aligned}&\sigma _{\gamma A\rightarrow J/\psi A}^\mathrm{VMD}(W_{\gamma p})\nonumber \\&\quad =\frac{\mathrm{d}\sigma _{\gamma p\rightarrow J/\psi p}(W_{\gamma p},t\!=\!0)}{\mathrm{d}t} \left[ {\frac{\sigma _{J/\psi A}^\mathrm{tot} (W_{\gamma p})}{A\sigma _{J/\psi N}^\mathrm{tot}(W_{\gamma p}) }}\right] ^2\!\! \varPhi _A(t_\mathrm{min}), \nonumber \\ \end{aligned}$$

(1)

where we assumed that the multiple interactions leading to the nuclear shadowing effect do not distort the shape of the transverse momentum distribution of the vector meson. In Eq. (1), $\varPhi _A(t_\mathrm{min})=\int ^{t_\mathrm{min}}_{-\infty }\mathrm{d}t \left| F_A (t)\right| ^2$, where $F_A (t)$ is the nucleus form factor (its normalization is $F_A (0)=A$) whose square takes into account that the nucleus remains intact in the coherent process, $t$ is the four-momentum transfer squared and $t_\mathrm{min}=-M_{J/\psi }^4 m_N^2/W_{\gamma p}^4$ is its minimal value ($M_{J/\psi }$ and $m_N$ are the masses of $J/\psi$ and the nucleon, respectively); $W_{\gamma p}$ is the photon–nucleus center-of-mass energy per nucleon; $\sigma _{J/\psi A}^\mathrm{tot}$ and $\sigma _{J/\psi N}^\mathrm{tot}$ are the total $J/\psi$–nucleus and $J/\psi$–nucleon cross sections, respectively. Note that in the first and second terms in Eq. (1), the dependence on $t_\mathrm{min}$ has been safely neglected compared to the $\varPhi _A(t_\mathrm{min})$ term.

In the optical limit of the Glauber model, the $\sigma _{J/\psi A}^\mathrm{tot}$ cross section is

$$\begin{aligned}&\sigma _{J/\psi A}^\mathrm{tot}(W_{\gamma p})\nonumber \\&\quad =2 \int \mathrm{d}^2{{{\varvec{b}}}} \left[ 1-\exp \left\{ -{{\sigma _{J/\psi N}(W_{\gamma p})T_A ({\mathbf{b}})}\over 2} \right\} \right] , \end{aligned}$$

(2)

where $T_A (\mathbf{b})=\int \mathrm{d}^2 \mathbf{b} \rho _A (\mathbf{b},z)$ is the nuclear width function; $\rho _A(\mathbf{b},z)$ is the nuclear density. Equation (2) describes successive multiple interactions of $J/\psi$ with target nucleons, whose destructive interference results in the nuclear attenuation (shadowing) [10] of the $J/\psi$–nucleus cross section, $\sigma _{J/\psi A}^\mathrm{tot} < A \sigma _{J/\psi N}^\mathrm{tot}$.

The main issue with Eqs. (1) and (2) is what value of the elementary $\sigma _{J/\psi N}^\mathrm{tot}$ cross section to use. It has been well known for a long time that if one tries to determine $\sigma _{J/\psi N}^\mathrm{tot}$ using the vector meson dominance model and the data on the elementary $\gamma p\rightarrow J/\psi p$ process, the obtained value of $\sigma _{J/\psi N}^\mathrm{tot}$ is small, namely, $\sigma _{J/\psi N}^\mathrm{tot}(W_{\gamma p}=5\, \mathrm{GeV}) \approx 1$ mb and $\sigma _{J/\psi N}^\mathrm{tot}(W_{\gamma p}=100\, \mathrm{GeV})\approx 3$ mb; see, e.g., [11]. As a result, the effect of nuclear shadowing in the $\sigma _{\gamma A\rightarrow J/\psi A}^\mathrm{VMD}$ cross section predicted using Eqs. (1) and (2) turns out to be small in the small-$x$ region, which contradicts the ALICE data. Also, the smallness of $\sigma _{J/\psi N}^\mathrm{tot}$ serves as an indication that in the strong interaction, $J/\psi$ reveals properties of a small-size dipole built from a heavy quark–antiquark pair.

The simple space-time picture of heavy onium production in the vector meson dominance model is superseded by the one in high-energy QCD, where the process of charmonium photoproduction involves three stages: (i) the photon conversion into a $q{\bar{q}}$ component (dipole) long before the target, (ii) the interaction of the dipole with the target, and (iii) the conversion of the $q{\bar{q}}$ component into the final state vector meson. This space-time picture is properly taken into account/realized in the framework of the QCD dipole approximation [12, 13], where the large mass of the $c$-quark, $m_c$, sets the hard scale in diffractive charmonium photoproduction, $\mu ^2\sim {\mathcal O}(m_c^2)$, and, thus, leads to the dominance of the dipoles of the small transverse size $d_t$, $d_t^2 \sim 1/\mu ^2$. The corresponding $q{{\bar{q}}}$ dipole–target cross section reads [14]:

$$\begin{aligned} \sigma _{q{{\bar{q}}}T}(d_t^2,x)=\frac{\pi ^2}{3}d_t^2 \alpha _s({\bar{Q}}^2)xG_T(x,{\bar{Q}}^2), \end{aligned}$$

(3)

where $\alpha _s$ is the running strong coupling constant; $G_T(x,{\bar{Q}}^2)$ is the gluon distribution in the target $T$, which depends on the momentum fraction $x=M_{J/\psi }^2/W_{\gamma p}^2$ ($M_{J/\psi }$ is the mass of $J/\psi$) and the hard scale squared ${\bar{Q}}^2 \propto 1/d_t^2 \sim {\mathcal O}(m_c^2)$.

In general, in the dipole approach, the $J/\psi$ photoproduction cross section involves dipoles of different transverse sizes $d_t$, which corresponds to different scales ${\bar{Q}}^2$ in Eq. (3). However, using the leading logarithmic approximation and making simplifying assumptions as regards the gluon transverse momentum ${\tilde{k}}_t$ (${\tilde{k}}_t^2 \ll \mu ^2$) and the $J/\psi$ wave function (assuming that the transverse momenta of $c$-quarks, $k_t$, are small ($k_t^2 \ll m_c^2$), while the longitudinal ones are equally shared between the $c$-quark and antiquark), it was shown that the imaginary part of the $J/\psi$ photoproduction amplitude involving the dipole cross section of Eq. (3) is expressed through the gluon density of the target at the scale of $\mu ^2=M_{J/\psi }^2/4=2.4~\hbox {GeV}^2$ and one obtains [15]:

$$\begin{aligned} \frac{\mathrm{d}\sigma _{\gamma T\rightarrow J/\psi T}(W_{\gamma p},t=0)}{\mathrm{d}t}=C({\mu }^2)\left[ xG_T (x,\mu ^2)\right] ^2, \end{aligned}$$

(4)

where $C(\mu ^2)=(1+\eta ^2)R_g^2 \,F^2(\mu ^2)M^3_{J/\psi }\varGamma _{ee} {\pi }^3 {\alpha _{s}}^2(\mu ^2 )/(48{\alpha _\mathrm{e.m.}}\mu ^8)$; $\varGamma _{ee}$ is the width of the $J/\psi$ electronic decay and $\alpha _\mathrm{e.m.}$ is the fine-structure constant. The factors of $\eta$ and $R_g$ correct Eq. (4) for the real part and the skewness of the $\gamma T \rightarrow J/\psi T$ scattering amplitude, respectively; the factor of $F^2(\mu ^2)$ absorbs all effects not included in the approximation used ($F^2(\mu ^2)=1$ in the non-relativistic limit for the $J/\psi$ wave function).

In a more general case [16], (i.e., beyond the $k_t^2 \ll m_c^2$ limit for the $J/\psi$ wave function), there exists a theoretical uncertainty in the value of $\mu ^2$ in Eq. (4) which means that one could use a reasonable range of values, e.g., $\mu ^2=2.4{-}3.4~\hbox {GeV}^2$. For example, the suitable value of $\mu ^2$ can be determined phenomenologically [4] comparing predictions of Eq. (4) for the proton target with the data.

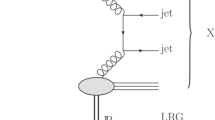
Working in the framework of the color dipole model, one can calculate the $\gamma A \rightarrow J/\psi A$ scattering amplitude by summing multiple rescatterings of a dipole of the fixed size $d_t$ on the target nucleons essentially using Eq. (2) and then integrating over $d_t$ with the weight given by the photon and $J/\psi$ wave functions [17]; see Fig. 1. Since, on average, $J/\psi$ photoproduction is dominated by small transverse size dipoles and the corresponding dipole–nucleon cross section (3) is small, the resulting nuclear shadowing is also small [18, 19], which contradicts the ALICE data; see the discussion in [4]. In this respect, the situation is similar to the VMD case considered above. In other words, in the dipole formalism, when only $q{{\bar{q}}}$-dipoles are included, nuclear shadowing in the $\gamma A \rightarrow J/\psi A$ scattering amplitude is a higher twist effect [20]. At the same time, the dipole approach describes reasonably well the RHIC UPC data corresponding to lower energies (larger values of $x$), where the effect of nuclear shadowing is rather small; see Fig. 5 and its discussion in Sect. 3.2.

Fig. 1

The multiple scattering series for the $\gamma A \rightarrow J/\psi A$ scattering amplitude in the color dipole formalism: a the impulse approximation, b the double scattering, c the interaction with three nucleons of the target

In contrast to the dipole formalism, one can use the leading twist framework of QCD factorization theorems, which enables one to apply Eq. (4) directly to nuclear targets. Applying Eq. (4) to the nucleus and proton targets, we obtain the following expression for the $t$-integrated cross section of coherent $J/\psi$ photoproduction on nuclei at high energy:

$$\begin{aligned}&\sigma _{\gamma A\rightarrow J/\psi A}^\mathrm{LTA}(W_{\gamma p})\nonumber \\&\quad =\frac{\mathrm{d}\sigma _{\gamma p\rightarrow J/\psi p}^\mathrm{pQCD}(W_{\gamma p},t=0)}{\mathrm{d}t} \left[ \frac{G_A(x,\mu ^2)}{AG_N(x,\mu ^2)}\right] ^2 \varPhi _A(t_\mathrm{min}), \nonumber \\ \end{aligned}$$

(5)

where $G_A(x,\mu ^2)$ and $G_N(x,\mu ^2)$ are the gluon distributions in a nucleus and the free proton, respectively; $\mathrm{d}\sigma _{\gamma p\rightarrow J/\psi p}^\mathrm{pQCD}(W_{\gamma p},t=0)/\mathrm{d}t$ is the perturbative QCD (pQCD) cross section on the proton calculated using Eq. (4). Thus, the nuclear modification (suppression) of $\sigma _{\gamma A\rightarrow J/\psi A}^\mathrm{LTA} (W_{\gamma p})$ is given by the factor of $R=G_A(x,\mu ^2)/[AG_N(x,\mu ^2)] < 1$ quantifying the amount of nuclear gluon shadowing at small $x$.

The leading twist theory of nuclear shadowing [6] is based on the space-time picture of the strong interaction at high energies, the generalization of the Gribov–Glauber theory of nuclear shadowing in soft hadron–nucleus scattering [10, 21] to hard processes with nuclei, and the QCD collinear factorization theorems for the total and diffractive cross sections of deep inelastic scattering (DIS). The approach allows one to make predictions for the leading twist shadowing correction to nuclear parton distributions (nPDFs), structure functions and cross sections, which are given as a series in the number of simultaneous interactions with the target nucleons (the multiple scattering series). The structure of each term in the series is unambiguously given by the Gribov–Glauber theory supplemented by Abramovsky–Gribov–Kancheli (AGK) cutting rules [22, 23] and the QCD factorization theorems.

In the graphic form, the multiple scattering series for the $\gamma A \rightarrow J/\psi A$ scattering amplitude in the leading twist theory of nuclear shadowing is shown in Fig. 2, where graph $a$ is the impulse approximation, graph $b$ corresponds to double scattering (the simultaneous interaction of the probe with two nucleons of the target), and graph $c$ corresponds to the interaction with three nucleons of the target.

Fig. 2

The multiple scattering series for the $\gamma A \rightarrow J/\psi A$ scattering amplitude in the leading twist theory of nuclear shadowing: a the impulse approximation, b the double scattering, c the interaction with three nucleons of the target

The multiple scattering series of Fig. 2 can be summed as follows. The Gribov result on the inelastic shadowing correction in hadron–nucleus scattering can be conveniently implemented using the formalism of cross section fluctuations [24]. In this approach, the interaction of a high-energy projectile with a nucleus is a two-step process. First, long before the target, the projectile fluctuates into different configurations interacting with a hadronic target with different cross sections $\sigma$ characterized by the distribution over cross sections $P(\sigma )$. Second, these fluctuations interact with the nucleus. The corresponding cross section is calculated separately for each fluctuation (for individual $\sigma$) using the Glauber method and then averaged with $P(\sigma )$; for details and references, see [6]. In particular, for the $\gamma A \rightarrow J/\psi A$ scattering amplitude, we obtain

$$\begin{aligned}&{\mathcal M}_{\gamma A \rightarrow J/\psi A}(t=0) =\varkappa \int _0^{\infty }\mathrm{d}\sigma P(\sigma ) \int \mathrm{d}^2 \mathbf{b}\left[ \frac{\sigma \, T_A(\mathbf{b})}{2}\!-\!\frac{\sigma ^2 \, T_A^2(\mathbf{b})}{2^2\, 2!}\!+\! \frac{\sigma ^3\, T_A^3(\mathbf{b})}{2^3\, 3!}- \cdots \right] \nonumber \\&\quad =\varkappa \int \mathrm{d}^2 \mathbf{b} \left[ \frac{\langle \sigma \rangle \, T_A(\mathbf{b})}{2}\!-\!\frac{\langle \sigma ^2 \rangle \, T_A^2(\mathbf{b})}{2^2\, 2!}\!+\! \frac{\langle \sigma ^3 \rangle \, T_A^3(\mathbf{b})}{2^3\, 3!} -\cdots \right] \!=\!\varkappa A \frac{\langle \sigma \rangle }{2} \left[ 1 \!-\!\frac{2}{A} \int \mathrm{d}^2 \mathbf{b} \left( \frac{\langle \sigma ^2 \rangle }{\langle \sigma \rangle } \frac{T_A^2(\mathbf{b})}{2^2\, 2!}\!-\! \frac{\langle \sigma ^2 \rangle }{\langle \sigma \rangle }\frac{\langle \sigma ^3 \rangle }{\langle \sigma ^2 \rangle } \frac{T_A^3(\mathbf{b})}{2^3\, 3!}+\cdots \right) \right] ,\nonumber \\ \end{aligned}$$

(6)

where $\langle \sigma ^N\rangle =\int \mathrm{d}\sigma P(\sigma )\sigma ^N$. The factor of $\varkappa$ contains the factors associated with the overlap of the photon and $J/\psi$ wave functions; its value is determined by the elementary $\gamma p \rightarrow J/\psi p$ cross section: $\mathrm{d}\sigma _{\gamma p \rightarrow J/\psi p}^\mathrm{pQCD}(t=0)/\mathrm{d}t=\varkappa ^2 \langle \sigma \rangle ^2/(16 \pi )$.

The first term in Eq. (6) describes photoproduction of $J/\psi$ on a single nucleon and, hence, is proportional to the number of nucleons $A$; it is the impulse approximation corresponding to graph $a$ in Fig. 2.

The second term in Eq. (6) corresponds to the simultaneous interaction of the hard probe with two nucleons of the target nucleus and gives the leading contribution to the shadowing correction; this term corresponds to graph $b$ in Fig. 2. According to the Gribov–Glauber theory of nuclear shadowing supplemented by the collinear factorization theorem for hard diffraction in deep inelastic scattering (DIS) [25], this contribution is unambiguously expressed in terms of elementary diffraction, notably, in terms of the diffractive gluon distribution of the proton $G_N^{D(3)}$ [26, 27]. The corresponding interaction cross section is $\sigma _2(x,\mu ^2)$:

$$\begin{aligned}&\frac{\langle \sigma ^2 \rangle }{\langle \sigma \rangle } \equiv \sigma _2(x,\mu ^2)\nonumber \\&\quad =\frac{16 \pi B_\mathrm{diff}}{(1+\eta ^2) xG_N(x,\mu ^2)} \int _x^{0.1} \mathrm{d}x_{I\!\!P} \beta G_N^{D(3)}(\beta ,\mu ^2,x_{I\!\!P}),\quad \end{aligned}$$

(7)

where $B_\mathrm{diff} \approx 6~\hbox {GeV}^{-2}$ is the slope of the $t$ dependence of the diffractive cross section; $\eta \approx 0.17$ is the ratio of the real to the imaginary parts of the diffractive scattering amplitude; the diffractive parton distribution $G_N^{D(3)}(\beta ,\mu ^2,x_{I\!\!P})$ depends on the two light-cone fractions: $x_{I\!\!P} \approx (M_X^2+\mu ^2)/W_{\gamma p}^2$ is the nucleon momentum fraction carried by the diffractive exchange presented by a zigzag line in Fig. 2 ($M_X$ is the invariant mass of the intermediate diffractive state) and $\beta =x/x_{I\!\!P}$ is the diffractive exchange (“Pomeron”) momentum fraction carried by the active parton.

The structure of the interaction with three and more nucleons of the target (graph $c$ in Fig. 2 and higher terms that we do not show) presents extension of that of graph $b$: in the interaction with $N$ nucleons of the target, the hard probe diffractively scatters off two nucleons of the target and the produced diffractive state rescatters on the remaining $N-2$ nucleons, which leads to its attenuation (absorption). In particular, the third term in Eq. (6) corresponds to the simultaneous interaction of the hard probe with three nucleons of the target; its contribution corresponds to graph $c$ in Fig. 2. This contribution cannot in general be expressed only in terms of diffractive distributions of the proton and needs to be modeled. Since the cross section of hard diffraction in $ep$ DIS exhibits the $W_{\gamma p}$ dependence typical for soft processes, it appears plausible to model the rescattering cross section responsible for the interaction with $N \ge 3$ nucleons (the solid circle in graph $c$ in Fig. 2) using the formalism of cross section fluctuations. Exactly this was assumed in Eq. (6); the corresponding effective cross section is

$$\begin{aligned} \frac{\langle \sigma ^3 \rangle }{\langle \sigma ^2 \rangle } \equiv \sigma _3, \end{aligned}$$

(8)

where we suppressed the $x$ and $\mu ^2$ dependence of $\sigma _3$ for brevity. In practice, the $\sigma _3$ cross section is calculated using the distribution $P(\sigma )$ modeled using the dipole formalism or $P_{\pi }(\sigma )$ of the pion, see details in [6]. This is reasonable at $\mu ^2 \sim$ few GeV$^2$, where soft physics dominates. For larger values of $\mu ^2$ (e.g., in the case of $\varUpsilon$ photoproduction), one can use Eq. (8) only as input at the low initial scale for the subsequent Dokshitzer–Gribov–Lipatov–Altarelli–Parisi (DGLAP) evolution to the desired value of $\mu ^2$.

For the interaction with $N \ge 4$ nucleons (not shown in Fig. 2), we assume that the effect of cross section fluctuations is the same as for the $N=3$ term, i.e., $\langle \sigma ^N \rangle =\langle \sigma ^2 \rangle \sigma _3^{N-2}=\langle \sigma \rangle \sigma _2 \sigma _3^{N-2}$ for $N \ge 3$.

With this input, the multiple scattering series in Eq. (6) can be summed and the result presented in the following compact form:

$$\begin{aligned}&{\mathcal M}_{\gamma A \rightarrow J/\psi A}(t=0)\nonumber \\&\quad \!=\! A \frac{\varkappa \langle \sigma \rangle }{2} \left[ 1\!-\!\frac{2}{A} \frac{\sigma _2}{\sigma _3^2} \int \mathrm{d}^2 \mathbf{b} \left( e^{-\sigma _3/2 T_A(b)} \!-\!1\!+\!\frac{\sigma _3}{2}T_A(b) \right) \!\right] \nonumber \\&\quad = A \frac{\varkappa \langle \sigma \rangle }{2} \left[ 1-\frac{\sigma _2}{\sigma _3}+ \frac{\sigma _2}{\sigma _3} \frac{\sigma ^A_3}{A \sigma _3}\right] , \end{aligned}$$

(9)

where $\sigma _3^A = 2 \int \mathrm{d}^2 \mathbf{b} (1-e^{-\sigma _3/2 T_A(b)})$ is the total hadron–nucleus cross section in the case when the total hadron–nucleon cross section is $\sigma _3$. Note that in Eq. (9) we did not take into account the small real part of the soft scattering amplitude corresponding to the $\sigma _3$ cross section, whose numerical effect is small.

Expressing the $\gamma A\rightarrow J/\psi A$ differential cross section in terms of the amplitude of Eq. (9), we obtain

$$\begin{aligned}&\sigma _{\gamma A\rightarrow J/\psi A}^\mathrm{LTA}(W_{\gamma p})\nonumber \\&\quad \!=\!\frac{\mathrm{d}\sigma _{\gamma p\rightarrow J/\psi p}^\mathrm{pQCD}(W_{\gamma p},t\!=\!0)}{\mathrm{d}t} \left[ 1\!-\!\frac{\sigma _2}{\sigma _3}\!+\! \frac{\sigma _2}{\sigma _3} \frac{\sigma ^A_3}{A \sigma _3} \right] ^2 \varPhi _A(t_\mathrm{min}). \nonumber \\ \end{aligned}$$

(10)

Note that the expression in the square brackets is nothing but the nuclear gluon shadowing ratio $R=G_A(x,\mu ^2)/[AG_N(x,\mu ^2)]$; i.e., Eqs. (10) and (5) are consistent with each other.

It is important to note that unlike the case of the color dipole formalism, the shadowing correction in Eq. (10) (and also in $R$) is a leading twist quantity determined by the elementary hard diffraction in lepton–proton DIS. In the low nuclear density limit, when the interaction with $N \ge 3$ nucleons can be neglected, the shadowing correction is driven by the leading twist $\sigma _2$ cross section. At the low values of $x$, the $N \ge 3$ terms also become important; their contributions are also leading twist quantities, which can be summed using the $\sigma _3$ cross section.

It is convenient to characterize the suppression of $\sigma _{\gamma A\rightarrow J/\psi A}^\mathrm{LTA} (W_{\gamma p})$ due to nuclear gluon shadowing in terms of the $S^\mathrm{LTA}_\mathrm{coh}(W_{\gamma p})$ ratio:

$$\begin{aligned} S^\mathrm{LTA}_\mathrm{coh}(W_{\gamma p})&\equiv \left[ \frac{\sigma ^\mathrm{LTA}_{\gamma A\rightarrow J/\psi A}(W_{\gamma p})}{\sigma ^\mathrm{IA}_{\gamma A\rightarrow J/\psi A}(W_{\gamma p})}\right] ^{1/2}\nonumber \\&= \left[ 1-\frac{\sigma _2}{\sigma _3}+ \frac{\sigma _2}{\sigma _3} \frac{\sigma ^A_3}{A \sigma _3}\right] =R(x,\mu ^2), \end{aligned}$$

(11)

where $\sigma ^\mathrm{IA}_{\gamma A\rightarrow J/\psi A}(W_{\gamma p})$ is the $\gamma A\rightarrow J/\psi A$ cross section in the impulse approximation (IA) neglecting all nuclear effects except for coherence:

$$\begin{aligned} \sigma _{\gamma A\rightarrow J/\psi A}^\mathrm{IA}(W_{\gamma p})=\frac{\mathrm{d}\sigma _{\gamma p\rightarrow J/\psi p}^\mathrm{pQCD}(W_{\gamma p},t=0)}{\mathrm{d}t} \varPhi _A(t_\mathrm{min}). \nonumber \\ \end{aligned}$$

(12)

Theoretical predictions for the suppression factor of $S^\mathrm{LTA}_\mathrm{coh}$ of Eq. (11) calculated using the leading twist theory of nuclear shadowing [6] and the EPS09 global QCD fits [5] agree well with the nuclear suppression factor obtained in the recent analysis of the ALICE data on coherent $J/\psi$ photoproduction in Pb–Pb UPCs at $x\approx 10^{-2}$ and $x\approx 10^{-3}$ [3, 4] (see also Fig. 4).

2.2 The incoherent nuclear $J/\psi$ photoproduction cross section

Similarly to the case of coherent $J/\psi$ photoproduction on nuclei considered in Sect. 2.1, the VMD model, the color dipole formalism and the leading twist approximation can be used to calculate the cross section of incoherent nuclear $J/\psi$ photoproduction, $\sigma _{\gamma A\rightarrow J/\psi A^{\prime }}$, where $A^{\prime }$ denotes the final nuclear state containing products of the nuclear disintegration ($A^{\prime } \ne A$). Using completeness of the $A^{\prime }$ states, in the high-energy optical limit of the Glauber model, the VMD model gives [9]:

$$\begin{aligned}&\frac{\sigma _{\gamma A\rightarrow J/\psi A^{\prime }}^\mathrm{VMD}(W_{\gamma p})}{\mathrm{d}t}\nonumber \\&\quad =\frac{\mathrm{d}\sigma _{\gamma p\rightarrow J/\psi p}(W_{\gamma p})}{\mathrm{d}t}\int \mathrm{d}^2 {\mathbf{b}}\, T_A(b) e^{-\sigma _{J/\psi N}^\mathrm{in}(W_{\gamma p}) T_A(b)}, \nonumber \\ \end{aligned}$$

(13)

where $\sigma _{J/\psi N}^\mathrm{in}=\sigma _{J/\psi N}-\sigma _{J/\psi N}^2/(16 \pi B_{J/\psi })$ is the inelastic $J/\psi$–nucleon cross section; $B_{J/\psi }$ is the slope of the $t$ dependence of the $\gamma p\rightarrow J/\psi p$ scattering amplitude. Note that Eq. (13) is valid at not too small $|t|\ne 0$.

Equation (13) has the straightforward and well-known interpretation: the probability of incoherent (quasielastic) photoproduction of a vector meson on a nucleus is given by the product of the probability of elastic scattering on a single nucleon times the probability for the produced vector meson to survive the passage through the nucleus on its way out. Since $\sigma _{J/\psi N}^\mathrm{in} \approx \sigma _{J/\psi N}$ is small, the nuclear suppression of $\sigma _{\gamma A\rightarrow J/\psi A^{\prime }}^\mathrm{VMD}$ due to nuclear shadowing is also small.

In the color dipole formalism, the coherent and incoherent nuclear $J/\psi$ photoproduction cross sections can be calculated on the same footing. The only difference is the order of averaging over the dipole sizes $d_t$: in the coherent case, one first averages the $\gamma A \rightarrow J/\psi A$ amplitude over $d_t$ and then squares the result, while in the incoherent case, one first squares the appropriate scattering amplitude and then averages the result over $d_t$, see, e.g., Ref. [19]. Since the relevant dipole cross section is small, similarly to the coherent case considered above, nuclear suppression of incoherent nuclear $J/\psi$ photoproduction cross sections is small [19]. At small $x$ typical for the LHC kinematics, $x \sim 10^{-3}$ and below, the dipole formalism predictions are subject to rather significant theoretical uncertainties due to the choice of the model for the dipole cross section and for the $J/\psi$ wave function. Nevertheless, one can still make the observation that the shadowing suppression of the incoherent cross section of $J/\psi$ photoproduction on nuclei appears to be larger than that for the coherent case. At the same time, in the RHIC kinematics corresponding to much larger values of $x$, $x \approx 10^{-2}$, where the effect of nuclear shadowing is small, both the dipole framework and the leading twist approach provide the good description of the PHENIX UPC data [28]. Note also that at $x \sim 10^{-2}$, numerous versions of the dipole model correspond to a similar color dipole cross section because the models have been fitted to the same data, see, e.g., Refs. [29, 30].

In the leading twist formalism, the cross section of incoherent $J/\psi$ photoproduction on nuclei can be readily calculated using the input employed in the coherent case (10). Generalizing the standard expression for the incoherent (quasielastic) nuclear cross section [9] to include cross section fluctuations, we obtain in the high-energy limit:

$$\begin{aligned}&\frac{\sigma _{\gamma A\rightarrow J/\psi A^{\prime }}^\mathrm{LTA}(W_{\gamma p})}{\mathrm{d}t}\nonumber \\&\quad =\varkappa ^2 e^{t B_{J/\psi }}\int \mathrm{d}^2 {\mathbf{b}}\, T_A(b)\int \mathrm{d}\sigma P(\sigma ) \int \mathrm{d} \sigma ^{\prime } P(\sigma ^{\prime }) \nonumber \\&\qquad \times \frac{\sigma \sigma ^{\prime }}{16 \pi } e^{-\sigma /2 T_A(b)} e^{-\sigma ^{\prime }/2 T_A(b)} e^{\sigma \sigma ^{\prime }/(16 \pi B_\mathrm{diff}) T_A(b)}. \end{aligned}$$

(14)

Note that in Eq. (14), averaging over cross section fluctuations should be performed at the amplitude level which explains presence of two integrals over $\sigma$ and $\sigma ^{\prime }$. Note also that in Eq. (14) we assumed that the slopes of the $t$ dependence of the soft scattering amplitudes corresponding to the $\sigma _2$ and $\sigma _3$ cross sections are equal; the numerical effect associated with the inequality of the slopes is negligibly small.

Recalling that $\mathrm{d}\sigma _{\gamma p \rightarrow J/\psi p}^\mathrm{pQCD}(t=0)/\mathrm{d}t=\varkappa ^2 \langle \sigma \rangle ^2/(16 \pi )$ and Eqs. (7) and (8), after some algebra, Eq. (14) can be written in the following compact form in terms of the $\sigma _2$ and $\sigma _3$ cross sections:

$$\begin{aligned}&\frac{\sigma _{\gamma A\rightarrow J/\psi A^{\prime }}^\mathrm{LTA}(W_{\gamma p})}{\mathrm{d}t}= \frac{\mathrm{d}\sigma _{\gamma p \rightarrow J/\psi p}^\mathrm{pQCD}(W_{\gamma p})}{\mathrm{d}t} \int \mathrm{d}^2 {\mathbf{b}}\, T_A(b) \nonumber \\&\qquad \times \left[ \left( 1\!-\!\frac{\sigma _2}{\sigma _3} \right) ^2\!+\!2\frac{\sigma _2}{\sigma _3}\left( 1\!-\! \frac{\sigma _2}{\sigma _3}\right) e^{-\sigma _3/2 T_A(b)}\right. \nonumber \\&\qquad \qquad \left. +\!\left( \frac{\sigma _2}{\sigma _3}\right) ^2 e^{-\sigma _3^\mathrm{in} T_A(b)}\right] \nonumber \\&\quad \approx \frac{\mathrm{d}\sigma _{\gamma p \rightarrow J/\psi p}^\mathrm{pQCD}(W_{\gamma p})}{\mathrm{d}t}\int \mathrm{d}^2 {\mathbf{b}}\, T_A(b)\nonumber \\&\quad \quad \quad \times \left[ 1\!-\!\frac{\sigma _2}{\sigma _3}\!+\!\frac{\sigma _2}{\sigma _3} e^{-\sigma _3/2 T_A(b)} \right] ^2, \end{aligned}$$

(15)

where $\sigma _3^\mathrm{in}=\sigma _3 -\sigma _3^2/(16 \pi B_\mathrm{diff})$. In the last line of Eq. (15) we used $\sigma _3^\mathrm{in} \approx \sigma _3$; we checked that this approximation works with high accuracy at the level of a few percent.

The physical interpretation of Eq. (15) is similar to that of Eqs. (9) and (11): the nuclear suppression factor in the square brackets arises from multiple interactions of the produced diffractive state with nucleons of the target, which are driven by the $\sigma _2$ and $\sigma _3$ cross sections.

A comparison of Eqs. (15) and (10) shows that in the leading twist approximation (LTA), nuclear suppression in both coherent and incoherent photoproduction is determined by the same quantities: $\sigma _{2}$ and $\sigma _{3}$ [see Eqs. (11) and (16)]. The $\sigma _{2}$ cross section is a model-independent quantity whose magnitude and $x$ dependence are fixed by the experimentally measured diffractive parton distributions, inclusive gluon distributions and DGLAP evolution equations; see Eq. (7). The $\sigma _{3}$ cross section is a model-dependent quantity of the LTA approach, whose value is constrained using the formalism of cross section fluctuations. In general, $\sigma _{3}\ge \sigma _{2}$ [see Eq. (8)]; the lower limit on the value of $\sigma _{3}$, $\sigma _{3}=\sigma _{2}$, corresponds to the upper limit on the predicted nuclear shadowing.

Equation (15) defines the shadowing suppression factor for incoherent nuclear $J/\psi$ photoproduction, $S_\mathrm{incoh}$:

$$\begin{aligned}&S_\mathrm{incoh}^\mathrm{LTA}(W_{\gamma p}) \equiv \frac{\mathrm{d}\sigma _{\gamma A \rightarrow J/\psi A^{\prime }}^\mathrm{LTA}(W_{\gamma p})/\mathrm{d}t}{A \mathrm{d}\sigma _{\gamma p \rightarrow J/\psi p}^\mathrm{pQCD}(W_{\gamma p})/\mathrm{d}t}\nonumber \\&\quad =\frac{1}{A} \int \mathrm{d}^2 {\mathbf{b}}\, T_A(b) \left[ 1-\frac{\sigma _2}{\sigma _3}+\frac{\sigma _2}{\sigma _3} e^{-\sigma _3/2 T_A(b)} \right] ^2. \end{aligned}$$

(16)

Note that Eqs. (15) and (16) are valid at not too small $|t| \ne 0$.

Figure 3 presents our predictions for $S_\mathrm{incoh}^\mathrm{LTA}$ as a function of $x=M_{J/\psi }^2/W_{\gamma p}^2$ for $^{208}$Pb at $\mu ^2=3~\hbox {GeV}^2$. The shaded band represents the theoretical uncertainty of our predictions associated with the range of possible values of the $\sigma _3$ cross section [6].

Fig. 3

The shadowing suppression factor for incoherent nuclear $J/\psi$ photoproduction, $S_\mathrm{incoh}^\mathrm{LTA}$, as a function of $x=M_{J/\psi }^2/W_{\gamma p}^2$ for $^{208}$Pb at $\mu ^2=3~\hbox {GeV}^2$. The shaded band is the theoretical uncertainty of our LTA approach

One should note that since both suppression factors of $S^\mathrm{LTA}_\mathrm{coh}$ (11) and $S_\mathrm{incoh}^\mathrm{LTA}$ (16) are determined by the essentially soft physics, we expect them to be numerically of a similar magnitude, with $S_\mathrm{incoh}^\mathrm{LTA}$ being somewhat smaller than $(S^\mathrm{LTA}_\mathrm{coh})^2$. Indeed, at $x=10^{-3}$ corresponding to $y \approx 0$ for Pb–Pb UPCs at $\sqrt{s_{NN}}=2.76~\hbox {GeV}$, we obtain $S_\mathrm{incoh}^\mathrm{LTA}=0.16{-}0.35$ from Fig. 3 and $(S_\mathrm{coh}^\mathrm{LTA})^2=0.35{-}0.43$ from Fig. 3 of Ref. [4].

3 Photoproduction of $J/\psi$ in Pb–Pb UPCs at the LHC

3.1 Coherent and incoherent cases

A high-energy nucleus–nucleus ultraperipheral collision takes place when the colliding ions pass each other at the distance $|{\mathbf{b}}|$ in the transverse plane (impact parameter) exceeding the sum of the nucleus radii, $|\mathbf{b}|>(2$–$3)R_A$, where $R_A$ is the nuclear radius (the UPC physics is reviewed in [31]). In this case, the strong interaction between the nuclei is suppressed and they interact electromagnetically via emission of quasi-real photons. Thus, nucleus–nucleus UPCs offer a possibility to probe very high-energy photon–nucleus scattering and, in particular, photoproduction of $J/\psi$ on nuclei. The corresponding cross section has the following form:

$$\begin{aligned} \frac{\mathrm{d}\sigma _{AA\rightarrow AA^{\prime }J/\psi }(y)}{\mathrm{d}y}&= N_{\gamma /A}(y)\sigma _{\gamma A\rightarrow J/\psi A^{\prime }}(y)\nonumber \\&+ N_{\gamma /A}(-y)\sigma _{\gamma A\rightarrow J/\psi A^{\prime }}(-y), \end{aligned}$$

(17)

where $N_{\gamma /A}(y)=\omega \mathrm{d}N_{\gamma /A}(\omega )/\mathrm{d}\omega$ is the photon flux; $y = \ln (2\omega /M_{J/\psi })$ is the $J/\psi$ rapidity, where $\omega$ is the photon energy and $M_{J/\psi }$ is the mass of $J/\psi$; $\sigma _{\gamma A\rightarrow J/\psi A^{\prime }}$ is the nuclear $J/\psi$ photoproduction cross section (see Sect. 2). Note that Eq. (17) includes both the case of coherent scattering without the nuclear breakup ($A^{\prime }=A$) and the case of incoherent (quasielastic) scattering when the final nucleus dissociates ($A^{\prime } \ne A$).

The photon flux at large impact parameters $b=|{\mathbf{b}}| > 2R_A$ emitted by a fast-moving nucleus, $N_{\gamma /A}(\omega )$, can be approximated very well by the following simple semi-classical expression for the flux of equivalent photons produced by a point-like particle with the electric charge $Z$:

$$\begin{aligned}&N_{\gamma /A}(\omega )=\frac{2Z^2\alpha _\mathrm{e.m.}}{\pi } \int _{2R_A}^{\infty } \mathrm{d}b\, \frac{X^2}{b}\left[ K^2_1(X)+\frac{1}{\gamma ^2_L} K^2_0(X)\right] ,\nonumber \\ \end{aligned}$$

(18)

where $\alpha _\mathrm{e.m.}$ is the fine-structure constant; $K_0(X)$ and $K_1(X)$ are modified Bessel functions; $X=b \omega /\gamma _L$, where $\gamma _L$ is the nucleus Lorentz factor. The strong interactions between the colliding nuclei is suppressed by the requirement that $b>2R_A$. Experimentally this corresponds to the selection of events with only two leptons from the $J/\psi$ decay and otherwise no charged particles in the whole rapidity range covered by the detector.

The presence of two terms in Eq. (17) reflects the fact that each nucleus can radiate a photon as well as can serve as a target. In the case of symmetric UPCs (e.g., in the case of Pb–Pb UPCs at the LHC and Au–Au UPCs at RHIC), at a fixed value of the $J/\psi$ rapidity $y \ne 0$, Eq. (17) contains two contributions: one corresponding to the interaction of high-energy photons with a nucleus and another corresponding to the interaction of low-energy photons with a nucleus.

In the coherent case, the separation of these overlapping contributions is not an easy problem since a priory one cannot say in the interaction with which of the two nuclei $J/\psi$ was produced. As a result, the photoproduction cross section $\sigma _{\gamma A\rightarrow J/\psi A}$ can be unambiguously extracted from the measured $\mathrm{d}\sigma _{AA\rightarrow AA J/\psi }(y)/\mathrm{d}y$ cross section only in the following two cases: (i) at $y=0$, where the two photon energies are equal and, hence, both terms in Eq. (17) contribute equally, and (ii) in the rapidity range where one of the contributions strongly dominates. Exactly this situation is realized in the ALICE experiment [1, 2]: the $\mathrm{d}\sigma _{AA\rightarrow AA J/\psi }(y)/\mathrm{d}y$ cross section was measured (i) for $-1<y<1$, which allowed one to extract $\sigma _{\gamma A\rightarrow J/\psi A}(W_{\gamma p})$ at $W_{\gamma p}\approx 100$ GeV corresponding to the gluon momentum fraction of $x\approx 10^{-3}$ ($W_{\gamma p}$ is the $\gamma$–nucleus center-of-mass energy per nucleon) and (ii) for $-4<y<-2.5$, where the low-energy photon contribution dominates (more than 95 %), which probes the nuclear gluon density at $x\approx 10^{-2}$.

As we already explained in the Introduction, the nuclear suppression factor for coherent nuclear $J/\psi$ photoproduction determined from the corresponding UPC cross section measured by the ALICE collaboration [3, 4] compares favorably with the theoretical models predicting large nuclear gluon shadowing, notably, with the leading twist approximation (LTA) [6] and with the EPS09 [5] result. This is illustrated in Fig. 4, where the ALICE data on the coherent $\mathrm{d}\sigma _{AA\rightarrow AAJ/\psi }(y)/\mathrm{d}y$ cross section at the central and forward values of the rapidity $|y|$ are compared to the LTA predictions combined with the CTEQ6L1 gluon parameterization [32] at $\mu ^2=3~\hbox {GeV}^2$. One can see from Fig. 4 that the theoretical calculations, which are made using Eqs. (10) and (17), describe the data well.

Fig. 4

The coherent $\mathrm{d}\sigma _{AA\rightarrow AAJ/\psi }(y)/\mathrm{d}y$ and incoherent $\mathrm{d}\sigma _{AA\rightarrow AA^{\prime }J/\psi }(y)/\mathrm{d}y$ cross sections as functions of the $J/\psi$ rapidity $y$ at $\sqrt{s}=2.76$ GeV. The ALICE data [1, 2] is compared to the LTA theoretical predictions; the bands span the uncertainty of the theoretical predictions

In the same figure, the LTA predictions for the incoherent $\mathrm{d}\sigma _{AA\rightarrow AA^{\prime }J/\psi }(y)/\mathrm{d}y$ cross section made using Eqs. (15) and (17) are compared to the ALICE data point at $|y|\approx 0$ [1]. One can see from the comparison that the LTA predicts the magnitude of suppression due to nuclear gluon shadowing exceeding the one seen in the data by approximately a factor of $1.5$.

The shaded bands in Fig. 4 represent the dominant theoretical uncertainty of the LTA predictions associated with the uncertainty in the value of the $\sigma _3$ cross section, which in turn results in the uncertainty of the LTA predictions for nuclear parton distributions [6]. The uncertainty associated with the value of the hard scale $\mu ^2$, which was studied in [4], is much smaller and has been safely neglected.

Note that in our calculations, we consider quasielastic scattering and do not take into account the incoherent contribution associated with the nucleon dissociation $\gamma +N \rightarrow J/\psi +Y$ [33]. We explained in the Introduction that this process could potentially contribute to the inelastic final state and, thus, affect the ALICE extraction of the incoherent $\mathrm{d}\sigma _{AA\rightarrow AA^{\prime }J/\psi }(y)/\mathrm{d}y$ cross section [1] due to the fact that the ALICE detector does not cover the full range of the rapidity $y$. While the calculation of the $\gamma +A \rightarrow J/\psi +Y+(A-1)^{*}$ contribution requires a a separate publication, one can still make several qualitative observations. First, this contribution is expected to have approximately the same $A$ dependence as that in Eq. (15) (it is proportional to $A$ in the impulse approximation). Second, the magnitude of this contribution is expected to be sizable: $(\mathrm{d}\sigma _{\gamma N \rightarrow J/\psi Y}/\mathrm{d}t)/(\mathrm{d}\sigma _{\gamma N \rightarrow J/\psi N}/\mathrm{d}t)\approx 0.15$ at $t \approx 0$ and increases with an increase of $|t|$ when the $\mathrm{d}\sigma _{\gamma N \rightarrow J/\psi Y}/\mathrm{d}t$ cross section becomes progressively more important and eventually exceeds that of the elastic $\gamma +N\rightarrow J/\psi +N$ process; $\sigma _{\gamma N\rightarrow J/\psi Y}/\sigma _{\gamma N \rightarrow J/\psi N} \approx 0.8$ for the $t$-integrated cross sections and for $M_Y < 10$ GeV ($M_Y$ is the invariant mass of the proton-dissociative system $Y$) [34]. It would be desirable to perform an additional analysis of the ALICE data [1] by assuming that the $\gamma +N \rightarrow J/\psi +N$ and $\gamma +N \rightarrow J/\psi +Y$ contributions to incoherent nuclear $J/\psi$ photoproduction have different slopes of the $t$ dependence, which would enable one to experimentally estimate the contribution of the nucleon dissociation and, thus, will enable a direct comparison of the data with predictions of Eq. (15). In addition, it is likely that due to the interaction of the system $Y$ with the nucleus, nucleon dissociation will lead to a larger number of neutrons originating from the nucleus dissociation. Finally, the study of neutron production in the quasielastic $\gamma A \rightarrow J/\psi A^{\prime }$ process at $|t| \ge 1~\hbox {GeV}^2$, where the $\gamma +N \rightarrow J/\psi +Y$ contribution dominates, may be interesting for understanding of the formation time in diffraction.

3.2 UPCs accompanied by neutron emission

Besides ALICE, the ATLAS and CMS detectors at the LHC are capable to measure UPC production of $J/\psi$ in the $-2.5<y<2.5$ range of rapidity. While for central rapidities, the interpretation of the corresponding measurements is unambiguous, it is difficult to disentangle the high-photon-energy and low-photon-energy contributions to $\mathrm{d}\sigma _{AA\rightarrow AAJ/\psi }(y)/\mathrm{d}y$ for non-central values of $y$ and, thus, to access the small-$x$ region that we are interested in. In particular, according to the estimates of [3, 4], for $1.5<|y|<2.5$ in Pb–Pb UPCs at 2.76 TeV, the $\mathrm{d}\sigma _{AA\rightarrow AAJ/\psi }(y)/\mathrm{d}y$ rapidity distribution in the coherent case is exceedingly dominated (by the factor of four) by the low-photon-energy contribution corresponding to $10^{-2} > x > 5 \times 10^{-3}$ of the probed nuclear gluons. The high-photon-energy contribution is suppressed by the much lower photon flux and the larger nuclear gluon shadowing. Hence, it is rather difficult to extract the high-energy nuclear coherent $J/\psi$ photoproduction cross section from the UPC data and, hence, to probe the nuclear gluon distribution around $x\approx 10^{-4}$.

The method to overcome this difficulty was suggested in [35]. It is based on the observation of [36] that coherent photoproduction of vector mesons in heavy ion UPCs can be accompanied by additional photon exchanges which lead to electromagnetic excitation of one or both nuclei with the subsequent neutron emission. These neutrons will have the energy close to that of the colliding beams and can be detected by zero degree calorimeters placed at large distances on both sides of the detectors. With the additional requirement to have in the final state only two muons from the $J/\psi$ decay (in addition to the neutrons) and the large rapidity gap, i.e., by requiring the absence of any other charged particle in the whole range of $y$ covered by the detector system, the strong interaction of the colliding nuclei should be suppressed.

To calculate the cross section of photoproduction of vector mesons in UPCs accompanied by the additional electromagnetic excitation of the colliding nuclei followed by their subsequent neutron emission, we use the model developed in [36]. This approach is justified by the success of the calculations of [37, 38] describing very well the ALICE data on electromagnetic dissociation in Pb–Pb UPCs [39]. The model is based on the assumption that an additional photon exchange does not destroy coherence of the photoproduction process but influences the impact parameter of the ultraperipheral collision. The latter is taken into account by the modification of the flux of the photons participating in photoproduction:

$$\begin{aligned} N_{\gamma /A}^i(\omega )= \int \limits _{2R_A}^{\infty } \mathrm{d}^2 {\mathbf{b}}\, N_{\gamma /A}(\omega ,\mathbf{b})P_{i}(\mathbf{b}), \end{aligned}$$

(19)

where the impact parameter dependent factor of $P_{i}(\mathbf{b})$ takes into account different channels of the nuclear decay by the neutron emission ($i=$ 0n0n, 0nXn, XnXn, $\ldots$). In particular, the 0n0n-channel corresponds to the selection of events without additional electromagnetic dissociation with the nucleus neutron decay; the 0nXn-channel corresponds to one-side excitation with the nucleus neutron decay of only one of the colliding nuclei; the XnXn-channel corresponds to mutual electromagnetic dissociation with both excited nuclei decaying by neutron emission. To obtain a rough estimate of the size of the effect, each additional photon exchange in Pb–Pb UPCs leads to the suppression of the cross section by the factor of $Z^{2}{\alpha }^{2}_\mathrm{e.m.} \approx 0.3{-}0.4$.

Based on the assumption that an additional photon exchange influences only the flux of photons, see Eq. (19), one can try to separate the low-energy ($\omega _1$) and high-energy ($\omega _2$) $J/\psi$ photoproduction contributions in the rapidity spectra measured in heavy ion UPCs. To this end, it is necessary [35] to measure rapidity distributions of vector meson production in any two channels, e.g., 0nXn and XnXn, and using the calculated photon fluxes for these channels, to solve simple equations at a fixed value of the rapidity $y$. For the coherent case, one then obtains

$$\begin{aligned} \begin{aligned} \mathrm{d}\sigma ^{0\mathrm{nXn}}/\mathrm{d}y&=N^{0\mathrm{nXn}}_{\gamma } (\omega _1) \sigma _{\gamma A\rightarrow J/\psi A} (\omega _1)\\&\quad +N^{0\mathrm{nXn}}_{\gamma } (\omega _2) \sigma _{\gamma A \rightarrow J/\psi A} (\omega _2), \\ \mathrm{d}\sigma ^{\mathrm{XnXn}}/\mathrm{d}y&=N^{\mathrm{XnXn}}_{\gamma } (\omega _1)\sigma _{\gamma A\rightarrow J/\psi A} (\omega _1)\\&\quad +N^{\mathrm{XnXn}}_{\gamma } (\omega _2) \sigma _{\gamma A \rightarrow J/\psi A}(\omega _2). \end{aligned} \end{aligned}$$

(20)

Since the photon fluxes $N^{0\mathrm{nXn}}_{\gamma }$ and $N^{\mathrm{XnXn}}_{\gamma }$ can be calculated with good accuracy, measurements of different channels will allow one to study nuclear gluon shadowing in a wide range of $x$. According to our calculations presented and discussed below, the relative contributions of low-photon-energy and high-photon-energy $J/\psi$ photoproduction in these channels are strongly different: while in the 0nXn-channel they are almost equal, the high-energy photoproduction dominates in the XnXn-channel.

Production of forward neutrons in quasielastic incoherent photoproduction of $J/\psi$ in heavy ion UPCs with the nuclear breakup has been considered in [40]. Since in this case the momentum transfer in elastic $J/\psi$ photoproduction on the nucleon can be as large as $|t|=1~\hbox {GeV}^2$, this target nucleon escaping from the nucleus participates in additional quasielastic rescattering. The average excitation energy of a heavy nucleus in the one-nucleon removal process is about $20{-}25$ MeV, which is much higher than the separation energy of $7{-}8$ MeV of one neutron. It was shown in [40] that in incoherent $J/\psi$ photoproduction in heavy ion UPCs, the residual nucleus will decay emitting one or more neutrons with the probability of about 85 %. Therefore, imposing the constraint that no neutrons are emitted, i.e., considering the 0n0n-channel, one can almost completely (at the level of 10–15 %) suppress the incoherent contribution.

As we mentioned in the end of Sect. 3.1, the contribution of nucleon dissociation becomes important/dominant with an increase of the transverse momentum of $J/\psi$. This process should lead to at least as many neutrons as the quasielastic process. Therefore, the $\gamma +N \rightarrow J/\psi +N$ and $\gamma +N \rightarrow J/\psi +Y$ contributions should be either separated experimentally or the latter should be included in the theoretical calculation of the $\gamma A \rightarrow J/\psi A^{\prime }$ cross section. The procedure for the extraction of the high-photon-energy contribution that we discuss below involves the use of the different $p_t$ dependences of the $\gamma +N \rightarrow J/\psi +N$ and $\gamma +N \rightarrow J/\psi +Y$ cross sections, which allows one to separate their contributions. We also note in passing that the study of the neutron multiplicity at $p_t \ge 0.8$ GeV, where the process of nucleon dissociation dominates, would produce for the first time information about the space-time formation of hadrons in the diffractive processes like $\gamma +N \rightarrow J/\psi +Y$.

The recent PHENIX data on $J/\psi$ photoproduction in ultraperipheral Au–Au collisions at 200 GeV accompanied by neutrons detected in both ZDCs [28, 41] gives an opportunity to check main assumptions as regards the sources of forward neutrons in coherent and incoherent $J/\psi$ photoproduction in heavy ion UPCs at high energies. Indeed, since the nuclear gluon shadowing in these processes is small at RHIC energies (the shadowing effect leads to an approximately 20 % reduction at the cross section level), the coherent and incoherent photoproduction cross sections can be calculated using either the dipole model or the leading twist approximation; at $x \sim 10^{-2}$ corresponding to the RHIC kinematics, the dipole model and LTA predictions largely converge. In this work, we use a simple version of the dipole model which employs the standard Glauber expressions [Eqs. (1) and (13)] with the elementary $\sigma _{J/\psi N}$ cross section approximated by the phenomenological Golec-Biernat–Wusthoff dipole cross section [42]. The resulting predictions are labeled “GBW+Glauber” in Fig. 5.

Fig. 5

The rapidity distribution of $J/\psi$ photoproduction in Au–Au UPCs with neutron emission in the XnXn-channel at $\sqrt{s}=200$ GeV. The PHENIX data [41] is compared to the theoretical prediction made using the simple dipole model described in the text (the curves labeled “GBW+Glauber”). The upper solid curve corresponds to the sum of the coherent and incoherent contributions; the lower dashed curve corresponds to the purely coherent contribution

It is worth noting here that for the discussed kinematics, the results for the dipole–nucleon cross section obtained in different dipole models are rather close since they are well constrained by the DIS data for these energies [29, 30]. The theoretical uncertainty is much smaller than the PHENIX experimental errors and, hence, it is not shown in Fig. 5. Note also that in the discussed model, the nuclear shadowing effect is driven by the $\sigma _{c{\bar{c}} N}$ dipole cross section and, hence, shadowing is suppressed (it is a higher twist effect) for the dipoles of such a small size; see the discussion above.

Selection of events with two-side neutron detection means that in the XnXn-channel, coherent production should take into account the mutual electromagnetic dissociation that requires at least two additional photon exchanges. In contrast, according to the predictions of [40], incoherent production is associated with excitation and neutron decay of only the target nucleus. Hence, in this case, detection of the XnXn-channel requires only one photon exchange to excite the nucleus, which serves as a source of the photon flux in the process of incoherent production.

Figure 5 presents a comparison of the PHENIX results for the XnXn-channel with our theoretical calculations using the simple dipole described above. Despite large experimental errors, it seems that the agreement between our calculations and the PHENIX data demonstrated in Fig. 5 justifies our approach to neutron production in UPCs. Coupling this with the good description of coherent $J/\psi$ photoproduction at the LHC makes our approach reasonable for the prediction of coherent and incoherent UPCs accompanied by neutron emission at the LHC.

Figure 6 presents the results of our calculation of the rapidity distributions in $J/\psi$ photoproduction in Pb–Pb UPCs with neutron emission in the 0nXn-channel (upper row of panels) and the XnXn-channel (lower row of panels) as functions of the rapidity $y$ at the LHC energy of ${\sqrt{s}_{NN}}=2.76$ GeV; the two panels on the left correspond to the coherent case and the panels on the right are for the incoherent case. Our theoretical predictions are made using the leading twist approximation (LTA); the shaded areas represent the dominant LTA theoretical uncertainty associated with the uncertainty in the predicted nuclear gluon distributions [6]. The uncertainty associated with the value of the hard scale $\mu ^2$ is much smaller and, hence, has been neglected.

Fig. 6

Predictions of the leading twist approximation (LTA) for the rapidity distribution of coherent (two left panels) and incoherent (two right panels) $J/\psi$ photoproduction in Pb–Pb UPCs with neutron emission in the 0nXn-channel (two upper panels) and in the XnXn-channel (two lower panels) at $\sqrt{s}=2.76$ GeV. The shaded bands represent the theoretical uncertainty of the LTA predictions

Each panel contains two sets of curves: the upper shaded area is a sum of the two terms in Eq. (17) and the lower shaded area represents the contribution of $J/\psi$ production by the photon emitted by the nucleus moving with the momentum in the direction of positive $J/\psi$ rapidity (the dashed curves labeled “one side”).

We can draw several conclusions from Fig. 6. First, one can see from the two left panels that using the data on the 0nXn and XnXn-channels, one can try to extract the high-photon-energy contribution using Eq. (20). In the range of rapidities of $1.5<y<2.5$, this will allow one to determine nuclear gluon shadowing in Pb down to $x\approx 10^{-4}$ and at the scale of $\mu ^2\approx 3~\hbox {GeV}^2$ from coherent $J/\psi$ photoproduction in UPCs.

Second, a comparison of the corresponding upper shaded areas in Fig. 6 shows that we predict that at central rapidities, (i) in the 0nXn-channel, the coherent and incoherent contributions will be practically of the same magnitude and (ii) in the XnXn-channel, the coherent contribution exceeds the incoherent one by approximately a factor of two.

Third, besides the coherent channel, the incoherent cross section can also be used to study nuclear gluon shadowing at small $x$. Based on the dominance of the strong interaction mechanism of neutron production in incoherent photoproduction, we predict that there is a good opportunity to separate the low-photon-energy and high-photon-energy contributions in the 0nXn-channel (see the upper right panel in Fig. 6). Indeed, since in this case neutrons are emitted by the target nucleus, there should by a correlation between the direction of the produced $J/\psi$ and the direction of neutrons in UPC events. In the kinematics of UPCs, the direction of charmonium produced by a high-energy photon and, hence, by low-$x$ gluons from the target, is opposite to the direction of the target nucleus and, correspondingly, to the direction of neutrons. Conversely, in the low-photon-energy production, the direction of charmonium coincides with the direction of the target and neutrons.

The standard procedure of the separation of coherent and incoherent events consists in the analysis of momentum transfer distributions. In coherent photoproduction, this distribution is dictated by the nuclear form factor squared and presents several distinct peaks at small $p_t <200$ MeV/c, where $p_t$ is the transverse momentum of produced $J/\psi$ and $t=-p_t^2$. One can see such first three diffractive peaks in Fig. 7. The $t$ dependence of the incoherent nuclear cross section is the same as in the elementary process, i.e., $\exp [-B_{J/\psi } |t|]$. Our predictions for the sum of the coherent and incoherent cross sections of $J/\psi$ photoproduction in Pb–Pb UPCs accompanied by neutron emission in the 0nXn-channel as a function of $p_t$ in the rapidity range of $1.5<y<2.5$ is shown in the upper panel of Fig. 7. As in Fig. 6, our theoretical predictions are based on the LTA; the shaded bands represent the LTA uncertainty in the predicted nuclear gluon distribution. In the figure, the peaks at small $p_t$ correspond to the coherent signal. Therefore, the $p_t <200$ MeV/c cut will effectively reject incoherent events with good accuracy.

As we already discussed above, the incoherent cross section can also probe the small-$x$ nuclear gluon distribution. In particular, in the 0nXn-channel, the directions of $J/\psi$ and the emitted neutrons can be unambiguously correlated with either the low-photon-energy or with the high-photon-energy contributions. At the same time, in the coherent channel, due to the assumption of independence of the processes of coherent photoproduction and electromagnetic dissociation followed by the nucleus neutron decay, it is impossible to assign emitting neutrons to the source or the target, and, hence, the probabilities to detect neutrons in the same and in the opposite direction with respect to the direction of $J/\psi$ should be equal.

Fig. 7

Upper panel Predictions for the sum of the coherent and incoherent cross section of $J/\psi$ photoproduction in Pb–Pb UPCs accompanied by neutron emission in the 0nXn-channel as a function of $p_t$ in the rapidity range of $1.5<y<2.5$. Middle panel The same quantity for the situation when the direction of $J/\psi$ coincides with that of the neutrons (upper band) and when the directions of $J/\psi$ are the neutrons are opposite (lower band). Bottom panel the ratio of the two curves from the middle panel. The shaded bands represent the theoretical uncertainty of the LTA predictions

These predictions are demonstrated in the middle panel of Fig. 7, where the upper band corresponds to the situation when the direction of $J/\psi$ coincides with that of the neutrons and the lower band is for the opposite directions of $J/\psi$ and the neutrons. The bottom panel shows the ratio of the two curves from the middle panel. Since we identify the events, where the directions of $J/\psi$ and neutrons are opposite, with high-energy photoproduction, there could be two sources of suppression of the corresponding cross section: (i) the falloff of the flux of high-energy photons emitted by the nucleus and (ii) stronger nuclear gluon shadowing of the small-$x$ gluons at $x \approx 10^{-4}$, which we are mainly interested in.

4 Conclusions

We considered $J/\psi$ photoproduction in ion–ion UPCs at the LHC and RHIC in the coherent and incoherent channels with and without accompanying forward neutron emission and analyzed the role of nuclear gluon shadowing at small $x$, $x=10^{-4}{-}10^{-2}$, in these processes. We extended the formalism of leading twist nuclear shadowing characterized by large nuclear gluon shadowing to the incoherent $\sigma _{\gamma A \rightarrow J/\psi A^{\prime }}$ cross section. We found that despite good agreement between the approaches predicting large nuclear gluon shadowing at $x \approx 10^{-3}$ and the large nuclear suppression factor extracted from the ALICE data on coherent $J/\psi$ photoproduction in Pb–Pb UPCs at the LHC [1, 2], in the incoherent channel, the leading twist approximation predicts the amount of nuclear suppression due to gluon shadowing which exceeds that seen in the data by approximately a factor of $1.5$ (Fig. 4). We hypothesize that one source of the discrepancy could be the contribution of incoherent nucleon dissociation, $\gamma N \rightarrow J/\psi Y$, which could potentially contribute to the ALICE data [1] and which is not taken into account in our theoretical analysis.

In coherent $J/\psi$ photoproduction in ion–ion UPCs, it is problematic (except for $y \approx 0$ and large $|y|$) to separate the contributions of high-energy and low-energy photons to the $\mathrm{d} \sigma _{AA\rightarrow AAJ/\psi }(y)/\mathrm{d}y$ cross section, which reduces the range of $x$ for the studies of small-$x$ nuclear gluon shadowing. This problem can be circumvented by considering $J/\psi$ photoproduction in ion–ion UPCs accompanied by neutron emission due to electromagnetic excitation of one or both colliding nuclei.

Using the leading twist approximation for nuclear gluon shadowing, we made predictions for coherent and incoherent nuclear $J/\psi$ photoproduction in Pb–Pb UPCs accompanied by neutron emission in various channels at the LHC (Fig. 6). In particular, we discuss the strategy allowing one to separate the low-photon-energy and the high-photon-energy contributions to coherent $J/\psi$ photoproduction performing a joint analysis of the data in the 0nXn and XnXn-channels. This gives an opportunity to shift the study of nuclear gluon shadowing to the lower $x$ region of $x \approx 10^{-4}$.

In addition, in the incoherent case accompanied by neutron emission, we show that the separation between the low-photon-energy and high-photon-energy contributions can be efficiently performed by measuring the correlation between the directions of $J/\psi$ and the emitted neutrons (Fig. 7).

In the kinematics where nuclear shadowing is small, we showed (Fig. 5) that theoretical predictions based on the dipole model agree with the PHENIX data on $J/\psi$ photoproduction in Au–Au UPCs at $\sqrt{s_{NN}}=200$ GeV in the XnXn-channel (both colliding nuclei emit neutrons detected in the ZDCs).