Model for melting transition of twisted DNA in a thermal bath

Abstract

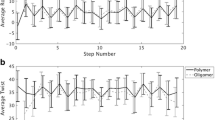
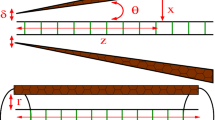
We investigated the melting transition of deoxyribonucleic acid (DNA) embedded in a Langevin fluctuation–dissipation thermal bath. Torsional effects were taken into consideration by introducing a twist angle $\varphi$ between neighboring base pairs stacked along the molecule backbone. We use the Barbi–Cocco–Payrard model to numerically study the impact of the twist angle on the melting temperature, considering four different sequences composed of 69 base pairs. According to the outcomes of our simulation, for all heterogeneous sequences, an increase in twist angle leads to a linear rise in melting temperature with a positive slope. For angles greater than the so-called equilibrium angle, the DNA chain becomes very rigid against opening and accordingly high temperatures are required to initiate the melting process. We also investigate the opening probability of bubbles, the bubble lifetime profiles and bubble length along the different DNA sequences.

Graphical abstract

Appendix: Rescaled equation of motion

The full analytical expression in Eq. (3) is given by

$$\begin{aligned} m \ddot{r}_{n}= & {} 2\alpha _n D_n\left( e^{-\alpha _n \left( r_n-R_0\right) }-1\right) e^{-\alpha _n (r_n-R_0)}\nonumber \\{} & {} -2K\left[ \left( L_{n,n-1}-L_0\right) \frac{r_n-r_{n-1}\cos \varphi }{L_{n,n-1}}\right. \nonumber \\{} & {} \quad \left. +\left( L_{n+1,n}-L_0\right) \frac{r_n-r_{n+1}\cos \varphi }{L_{n+1,n}}\right] \nonumber \\{} & {} +Se^{-\beta \left( r_n+r_{n-1}-2R_0\right) }\left( r_n-r_{n-1}\right) \left[ \beta \left( r_n-r_{n-1}\right) -2\right] \nonumber \\{} & {} +Se^{-\beta \left( r_{n+1}+r_n-2R_0\right) }\left( r_{n+1}-r_n\right) \left[ \beta \left( r_{n+1}-r_n\right) +2\right] .\nonumber \\ \end{aligned}$$

(8)

Introducing the dimensionless stretching of the base pairs as $\tilde{r}_n=\alpha r_n$, $\tilde{R}_0=\alpha R_0$ and substituting $b=\frac{\beta }{\alpha }$ and $a_n=\frac{\alpha _n}{\alpha }$, we can rewrite the equation of motion as

$$\begin{aligned} m \frac{\textrm{d}^2\tilde{r}_n}{\textrm{d}t^2}= & {} 2\alpha \alpha _n D_n\left( e^{-a_n \left( \tilde{r}_n-\tilde{R}_0\right) }-1\right) e^{-a_n \left( \tilde{r}_n-\tilde{R}_0\right) }\nonumber \\{} & {} -2K\left[ \left( \tilde{L}_{n,n-1}-\tilde{L}_0\right) \frac{\tilde{r}_n-\tilde{r}_{n-1}\cos \varphi }{\tilde{L}_{n,n-1}}\right. \nonumber \\{} & {} \left. +\left( \tilde{L}_{n+1,n}-\tilde{L}_0\right) \frac{\tilde{r}_n-\tilde{r}_{n+1}\cos \varphi }{\tilde{L}_{n+1,n}}\right] \nonumber \\{} & {} +Se^{-b\left( \tilde{r}_n+\tilde{r}_{n-1}-2\tilde{R}_0\right) }\left( \tilde{r}_n-\tilde{r}_{n-1}\right) \nonumber \\{} & {} \times \left[ b\left( \tilde{r}_n-\tilde{r}_{n-1}\right) -2\right] \nonumber \\{} & {} +Se^{-b\left( \tilde{r}_{n+1}+\tilde{r}_n-2\tilde{R}_0\right) }(\tilde{r}_{n+1}-\tilde{r}_n)\nonumber \\{} & {} \times \left[ b\left( \tilde{r}_{n+1}-\tilde{r}_n\right) +2\right] \nonumber \\{} & {} -m\gamma \frac{\textrm{d}\tilde{r}_n}{\textrm{d}t}+\alpha \sqrt{2\gamma m k_\texttt {B} T}\;\xi _n(t). \end{aligned}$$

(9)

Next, we introduce the dimensionless time $\tau =\sqrt{\frac{D\alpha ^2}{m}}t$ and the substitutions $\lambda _n=\frac{D_n\alpha _n}{D\alpha }$, so that

$$\begin{aligned} \frac{\textrm{d}^2\tilde{r}_n}{\textrm{d}\tau ^2}= & {} 2\lambda _n\left( e^{-a_n \left( \tilde{r}_n-\tilde{R}_0\right) }-1\right) e^{-a_n \left( \tilde{r}_n-\tilde{R}_0\right) }\nonumber \\{} & {} -2\frac{K}{D\alpha ^2}\left[ \left( \tilde{L}_{n,n-1}-\tilde{L}_0\right) \frac{\tilde{r}_n-\tilde{r}_{n-1}\cos \varphi }{\tilde{L}_{n,n-1}}\right. \nonumber \\{} & {} \left. +\left( \tilde{L}_{n+1,n}-\tilde{L}_0\right) \frac{\tilde{r}_n-\tilde{r}_{n+1}\cos \varphi }{\tilde{L}_{n+1,n}}\right] +\frac{S}{D\alpha ^2}\nonumber \\{} & {} \times e^{-b\left( \tilde{r}_n+\tilde{r}_{n-1}-2\tilde{R}_0\right) }\left( \tilde{r}_n-\tilde{r}_{n-1}\right) \left[ b\left( \tilde{r}_n-\tilde{r}_{n-1}\right) -2\right] \nonumber \\{} & {} +\frac{S}{D\alpha ^2}e^{-b\left( \tilde{r}_{n+1}+\tilde{r}_n-2\tilde{R}_0\right) }\left( \tilde{r}_{n+1}-\tilde{r}_n\right) \nonumber \\{} & {} \times \left[ b\left( \tilde{r}_{n+1}-\tilde{r}_n\right) +2\right] \nonumber \\{} & {} -\gamma \sqrt{\frac{m}{D\alpha ^2}}\frac{dr_n}{d\tau }+\frac{\sqrt{2\gamma m k_BT}}{D\alpha }\xi _n\left( \sqrt{\frac{m}{D\alpha ^2}}\tau \right) . \end{aligned}$$

(10)

Finally, in the former equation we rewrite the noise term as

$$\begin{aligned} \xi \left( \sqrt{\frac{m}{D\alpha ^2}}\tau \right) \rightarrow \root 4 \of {\frac{D\alpha ^2}{m}}\xi (\tau ), \end{aligned}$$

(11)

which is justified due to Dirac delta function and Gaussian noise properties, $\langle \xi _n(A\tau )\xi _n(A\tau ^{\prime }) \rangle = A^{-1} \delta (\tau -\tau ^{\prime })$ and $\xi (A\tau )\rightarrow \frac{1}{\sqrt{A}}\xi (\tau )$, respectively.

By considering

$$\begin{aligned}{} & {} F_n\left( \tilde{r}_{n-1},\tilde{r}_n,\tilde{r}_{n+1}\right) = 2\lambda _n\left( e^{-a_n (\tilde{r}_n-\tilde{R}_0)}-1\right) e^{-a_n \left( \tilde{r}_n-\tilde{R}_0\right) }\nonumber \\{} & {} -2\tilde{K}\left[ \left( \tilde{L}_{n,n-1}-\tilde{L}_0\right) \frac{\tilde{r}_n-\tilde{r}_{n-1} \cos \varphi }{\tilde{L}_{n,n-1}}\right. \nonumber \\{} & {} \left. +\left( \tilde{L}_{n+1,n}-\tilde{L}_0\right) \frac{\tilde{r}_n-\tilde{r}_{n+1} \cos \varphi }{\tilde{L}_{n+1,n}}\right] \nonumber \\{} & {} +\tilde{S}e^{-b\left( \tilde{r}_n+\tilde{r}_{n-1}-2\tilde{R}_0\right) }\left( \tilde{r}_n-\tilde{r}_{n-1}\right) \left[ b\left( \tilde{r}_n-\tilde{r}_{n-1}\right) -2\right] \nonumber \\{} & {} +\tilde{S}e^{-b\left( \tilde{r}_{n+1}+\tilde{r}_n-2\tilde{R}_0\right) }\left( \tilde{r}_{n+1}-\tilde{r}_n\right) \left[ b\left( \tilde{r}_{n+1}-\tilde{r}_n\right) +2\right] , \end{aligned}$$

(12)

and substituting Eq. (11) into Eq. (10), we are led to Eq. (5) in the text, namely

$$\begin{aligned} \frac{\textrm{d}^2\tilde{r}_n}{\textrm{d}\tau ^2} = F_n(\tilde{r}_{n-1},\tilde{r}_n,\tilde{r}_{n+1})-\Gamma \frac{d \tilde{r}_n}{d \tau }+\sqrt{2\Gamma \mathcal {E}} \xi _n(\tau ). \end{aligned}$$