Statistics of Floquet quasienergy spectrum for one-dimensional periodic, Fibonacci quasiperiodic and random discrete-time quantum walks

Abstract

Discrete-time quantum walks are Floquet systems if the quantum walk operator is independent of time. We consider such one-dimensional quantum walks with two quantum coin operators arranged in discrete space according to periodic, Fibonacci quasiperiodic and random sequences. We explore the correlation dimension of Floquet quasienergy spectrum, Floquet level spacing ratio and inverse participation ratio of Floquet states, respectively. We find they increase with spreading exponent and surviving exponent, so the statistics of Floquet quasienergy is an effective quantity to reflect dynamical properties in quantum transport of discrete-time quantum walks. We also contrast the differences among the three kinds of quantum walks.

Graphic abstract

Appendices

Appendix A: Correlation dimension in different system sizes

Fig. 5

Correlation dimension $D_c$ as functions of $\theta _2$ for a periodic and b Fibonacci DTQWs

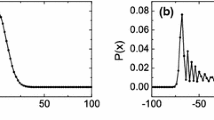
At different system sizes N, the dependence of correlation dimension $D_c$ on $\theta _2$ are given in Fig. 5. Here, we present $D_c$ for periodic and Fibonacci DTQWs. For random DTQWs, the corresponding Floquet quasienergy spectrum is point spectrum [21] and the “pointwise” method to calculate $D_c$ [55] can not properly determine its correlation dimension. Fig. 5 shows $D_c$ decreases with N. The difference of $D_c$ for different N is reduced as N increases, so we expect the values of $D_c$ will eventually reach asymptotic ones at larger N.

Appendix B: Floquet level spacing ratio in different system sizes

Fig. 6

Floquet level spacing ratio $\langle {r}\rangle$ as functions of $\theta _2$ for a periodic, b Fibonacci and c random DTQWs, respectively

At different system sizes N, the dependence of Floquet level spacing ratio $\langle {r}\rangle$ on $\theta _2$ are given in Fig. 6. For periodic DTQWs, Fig. 6a shows except at $\theta _2=\pi /2$ and $3\pi /2$ (states are localized), $\langle {r}\rangle$ slightly increases with N and it approaches to ones for larger N, which reflects these states are extended [58]. For Fibonacci DTQWs, Fig. 6b shows $\langle {r}\rangle$ may slightly decreases ($0\le \theta _2<\pi /4$ and $3\pi /4<\theta _2\le 2\pi$) or slightly increases ($\pi /4<\theta _2<3\pi /4$) with N. As the spectrum is singular continuous ones, $\langle {r}\rangle$ is sensitive to system size N. In contrast, for random DTQWs, Fig. 6c shows except at $\theta _2=\pi /4$ and $3\pi /4$ (states are extended), $\langle {r}\rangle$ slightly decreases with N or almost does not change. And most values of $\langle {r}\rangle$ is nearly equal to or less than 0.386, which means these states are localized [58].

Appendix C: Approximate fractal dimension in different system sizes

Fig. 7

Approximate fractal dimension $\varGamma$ as functions of $\theta _2$ for a periodic, b Fibonacci and c random DTQWs, respectively

At different system sizes N, the dependence of approximate fractal dimension $\varGamma$ on $\theta _2$ are given in Fig. 7. It is known that $\varGamma \rightarrow 1$ for extended states and $\varGamma \rightarrow 0$ for localized states [64]. For periodic DTQWs, Fig. 7a shows $\varGamma$ is relative large and it increases with N, which means these states are extended; at $\theta _2=\pi /2$ and $3\pi /2$, $\varGamma$ is relative small though it slightly increases with N, and such states correspond to localized states. For Fibonacci DTQWs, Fig. 7b shows as $\theta _2$ is apart from $\pi /4$ and $3\pi /4$, $\varGamma$ is intermediate and the difference of $\varGamma$ for different N almost disappears as N increases, which means these states are critical. The results for random DTQW are shown in Fig. 7c, where 500, 300 and 100 disorder realizations are applied for system sizes $N=500, 1000$ and 2000, respectively. It shows except at $\theta _2=\pi /4$ and $3\pi /4$ (states are extended), $\varGamma$ is relatively small and it decreases with N, which means these states are localized.