Theory for cuprate high-temperature superconductors in the underdoped regime: the singlet-bond superconductivity

Abstract

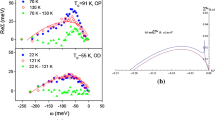
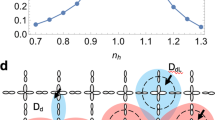
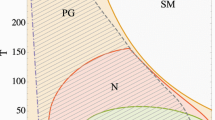
In the large U Hubbard model, the singlet-bond state (the two-electron bound state) different from the resonating valence bond (RVB) state is found to exist. Upon doping holes into the half-filled Hubbard model, the singlet-bond state changes from the immobile state to the translationally mobile state and the coherent singlet-bond superconducting state develops below the disordered immobile singlet-bond insulating phase. The superconducting phase has the doubled-size sublattice symmetry similar to the antiferromagnetic phase. The sublattice quasiparticle energy dispersions of the singlet-bond superconducting state can explain the experimentally observed unusual small hole-like Fermi pockets around $(\pm \frac{\pi }{2},\pm \frac{\pi }{2})$ and are consistent with the ARPES spectra observed in the zone-face and the zone-diagonal directions. The superconducting transition temperature is determined as $k_{B}T_{c}(\delta )=\frac{3}{\ln \gamma (\delta )}J\delta$, where $\delta$ is doping, $J\equiv \frac{4t^{2}}{U}$, and $\frac{3}{\ln \gamma (\delta )}$ varies monotonically from 3.77 for $\delta =0$ to 2.42 for $\delta =0.2$.

Graphical abstract

Appendix: Calculation of \(\Gamma (\delta )\)

We divide the whole square lattice into the four groups of diamonds (labeled 1, 2, 3, 4), each diamond containing one electron on each of the 4 vertex sites and one on the center site as shown in Fig. 4. The diamonds of the same group are so chosen that the vertices do not overlap between different diamonds. The four groups 1–4 are geometrically equal so the number of diamonds in each group is the same, $N_{1}=N_{2}=N_{3}=N_{4}$.

First, we calculate $\Gamma (0)$ for the undoped case $\delta =0$ that each lattice site is occupied by one electron. Each diamond of any group can have only one singlet-bond and there are four such cases to have a singlet-bond between the center electron and one of the four surrounding vertex electrons. We count the number of possible arrangements of singlet-bond placement in each group, one by one, in such a way that after the counting is finished for group 1, we count the number for group 2, and so on. First, in group 1, each diamond can have four possible singlet-bond placements independent of the other diamonds, so giving in total $4^{N_{1}}$ for the number of arrangements in group 1. Next, in group 2, each vertex of the diamond is shared with the diamonds of group 1 so the probability for the center site to make a singlet-bond with each of the vertex sites is reduced from 1 to $1-\frac{1}{4}$. Therefore, each diamond can have $(1-\frac{1}{4})\times 4$ singlet-bond placements and the total arrangements are $[(1-\frac{1}{4})\times 4]^{N_{2}}$. Similarly, the diamond in group 3 shares its vertex with two other diamonds belonging to groups 1 and in 2 so the arrangements are $[(1-\frac{1}{4}-\frac{1}{4})\times 4]^{N_{3}}$. In addition, in group 4, each vertex is shared with the other three groups 1, 2, and 3 and the arrangements are $[(1-\frac{1}{4}-\frac{1}{4}-\frac{1}{4})\times 4]^{N_{4}}$. These four arrangements’ numbers are multiplied to obtain the total number of all possible random singlet-bond arrangements $\Gamma (\delta =0)$ as they have been obtained independent of the other arrangements. Since the total number of the diamonds included in all the groups, $N_{1}+N_{2}+N_{3}+N_{4}=4N_{1}$, is equal to the number of singlet bonds, $N_{sb}(0)=\frac{N}{2}$, $\Gamma (\delta =0)$ is written as

$$\begin{aligned} \Gamma (\delta =0)= & {} 4^{N_{1}}3^{N_{2}}2^{N_{3}}1^{N_{4}}=(4!)^{\frac{1}{4}\frac{N}{2}}=2.21^{\frac{N}{2}} \nonumber \\\equiv & {} \gamma (\delta =0)^{\frac{N}{2}}, \end{aligned}$$

(A.1)

which defines $\gamma (\delta =0)$.

Fig. 4

The undoped two-dimensional square lattice is divided into the four groups 1–4 of diamonds (bold lines). Each diamond has one electron at the center site and one electron at each of the surrounding four vertex sites and can make only one singlet-bond

In the $\delta$ doped system, $\frac{N}{2}\delta$ singlet bonds are destroyed by $N\delta$ doped holes. These broken bonds must be equally distributed with the same number $\frac{N}{2}\frac{\delta }{4}=N_{1}\delta \equiv \Delta N_{1}$ into the four diamond groups. Therefore, the remaining singlet-bond number in each group is $N_{1}-\Delta N_{1}=N_{1}(1-\delta )$. The number of the combination to select diamonds in which singlet bonds are not destroyed is the same in all the groups and is given by $C_{N_{1},N_{1}(1-\delta )}=\frac{N_{1}!}{(N_{1}\delta )!(N_{1}(1-\delta ))!}=\delta ^{-N_{1}\delta }(1-\delta )^{-N_{1}(1-\delta )}$ which is hereafter written as C. The number of the singlet bonds arrangements for the bond-remaining diamonds in group 1 is $4^{N_{1}(1-\delta )}$ similar to the $\delta =0$ case but for groups 2, 3, and 4 one must take into account the fact that if the previous group diamonds sharing vertices with the one under consideration are doped with holes, the possible singlet-bond placement number is increased by 1 if the vertices are shared by 2 groups, increased by 2 if shared by 3 groups, and increased by 3 if shared by 4 groups. Accordingly $\Gamma (\delta )$ is given by $\Gamma (\delta )=[C4^{N_{1}(1-\delta )}][C\{(1-\delta )\times 3+\delta \times 4\}^{N_{1}(1-\delta )}][C\{(1-\delta )^{2}\times 2+2(1-\delta )\delta \times 3+\delta ^{2}\times 4\}][C\{(1-\delta )^{3}\times 1+3(1-\delta )^{2}\delta \times 2+3(1-\delta )\delta ^{2}\times 3+\delta ^{3}\times 4\}^{N_{1}(1-\delta )}]$. Therefore, $\Gamma (\delta )$ and thus $\ln \gamma (\delta )$ are obtained as

$$\begin{aligned}&\Gamma (\delta )=C^{4}[4!]^{\frac{N}{8}(1-\delta )}\nonumber \\&\quad \times \left[ \left( 1+\frac{\delta }{3}\right) \left( 1+\delta \right) \left( 1+3\delta \right) \right] ^{\frac{N}{8}(1-\delta )}, \end{aligned}$$

(A.2)

and

$$\begin{aligned} \ln \gamma \left( \delta \right)= & {} 0.795+0.205\delta -\delta ^{2}+\frac{1}{4}\left( 1-\delta \right) \ln \left( 1+\frac{13}{3}\delta \right) \nonumber \\&+\delta |\ln \delta |. \end{aligned}$$

(A.3)