1 Introduction

Studies of QED radiative corrections in electron-induced nuclear reactions have a long history, starting in 1949 with the first calculation by Schwinger [1]. Radiative corrections have been most extensively studied in the case of e–p scattering [2,3,4,5,6,7,8]. The success of calculations in the interpretation of virtual Compton scattering experiments [9, 10] as well as in the determination of proton charge form-factors [11, 12] has motivated us to extend the effort also to the electron-nucleus scattering.

We are particularly interested in a precise understanding of the radiative corrections in electron-induced nuclear reactions on \({}^{12}\textrm{C}\), which are relevant for all experiments that are aiming at measuring cross-sections with systematic precisions at the level of a few percent. One such example is the determination of the transition form-factors of the excited states of carbon, in particular the Hoyle state. The measured cross-sections for these states can be strongly contaminated by the radiative tail of the dominant elastic peak [13] and could limit the precision of the extracted form-factors from the upcoming electron scattering experiments like MAGIX [14], and thus the efforts to understand the structure of the Hoyle state.

A detailed description of QED radiative corrections is also important to ensure a reliable analysis of scattering data that are relevant for studying neutrinos. The interpretation of the signals measured in neutrino experiments relies on Monte-Carlo (MC) simulations of neutrino interactions with nuclei inside the detector volume. Hence, a tremendous effort is currently being invested to develop MC event generators [15, 16] together with the corresponding models of the nuclear interaction [17,18,19] that are capable of providing a full description of the neutrino-nucleus cross-sections for energies between a few tens of \(\textrm{MeV}\) and a few \(\textrm{GeV}\). The models are tested on the available electron-carbon scattering data [20], which, at small energies and small electron scattering angles, are very sparse, inconclusive and contaminated by the radiative tail of the elastic peak [21]. To overcome this problem and ensure precise tests of the available theoretical calculations, new precise cross-section measurements at \(Q^2 \lesssim 0.1\,\mathrm {GeV^2/c^2}\) are thus needed, together with a reliable simulation of the radiative corrections going beyond the peaking approximation.

A precise understanding of the radiative corrections for elastic electron-carbon scattering also opens a possibility of using thin plastic (polyethylene) foils as effective hydrogen targets in the proton-charge form-factor measurements at low values of four-momentum transfers \((Q^2\approx 10^{-3}\,\textrm{GeV}^2/\text {c}^2)\), where the cross-sections for nuclear excitations and quasi-elastic scattering are small [22]. Hence, the experimental background of the hydrogen elastic cross-section measurement would be dominated by events from the reaction \({}^{12}\textrm{C} + e \rightarrow {}^{12}\textrm{C}+ e' + \gamma \). If a simulation of such QED processes with a relative precision of \(1\,\mathrm {\%}\) would be available for background subtraction in regions where \(\Delta E_{e'} = E_{e'}^{\textrm{elastic}} - E_{e'} \gg 1\,\textrm{MeV}\), then the use of a solid-state target would represent a significant experimental advantage compared to the use of traditional extended cryogenic targets [12].

2 The elastic radiative tail

The radiative tail of elastic electron-nucleus scattering observed in the measured spectra arises from processes where one or more real photons are radiated from the charged particles. The dominant contributions to the elastic radiative tail are the two Bethe-Heitler diagrams shown in Fig. 1, where a photon is emitted by either the incident (BH-i) or final (BH-f) electron [7].

Fig. 1
figure 1

Feynman diagrams for Bethe-Heitler processes for scattering of an electron from a nucleus. In these reactions a real photon is emitted by either the incident (BH-i) or the final (BH-f) electron

Full size image

Since the emitted photon carries away a fraction of the energy, the energy of the scattered electron, \(E_{e'}\), is lower than the energy of the elastically scattered electron, \(E_{e'}^{\textrm{elastic}}\). In elastic electron-nucleus scattering experiments this causes the measured cross-section \(({d\sigma }/{d\Omega })_\textrm{exp}\) to be smaller than the elastic cross-section \(({d\sigma }/{d\Omega })_0\), predominantly because some of the electrons miss the finite energy acceptance of the detector [7]. This difference is encompassed in the relative radiative correction factor \(\delta \), such that:

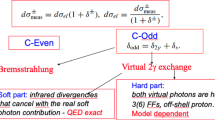
$$\begin{aligned} \left( \frac{d\sigma }{d\Omega }\right) _\textrm{exp} = \left( \frac{d\sigma }{d\Omega }\right) _\textrm{0} (1+\delta ). \end{aligned}$$
(1)

See Appendix A. Exact theoretical calculations of radiative correction factor are continuously improving and at the moment encompass calculations of first and second order processes, including one- and two-loop corrections, radiation of one and two photons and one-loop corrections for one-photon radiation [8, 23].

Unfortunately, the effective corrections to the elastic cross-section obtained with the available calculations cannot be used in the analyses of the inelastic cross-sections to reliably estimate the background in the measured spectra caused by the elastic radiative tail. For that one needs an event-by-event simulation that will mimic the measurement of inelastic process \({}^{12}\textrm{C} + e \rightarrow {}^{12}\textrm{C}+ e' + \gamma \) and will generate all observables (energies, angles, ...) in the same way as an experiment would. Hence, the goal of this work was to construct a generator of events that could be used for a reliable subtraction of the background when investigating inclusive inelastic scattering processes.

3 The event generator

For simulating the radiative background the analysis packages are predominantly using the peaking approximation discussed in Appendix B. The use of peaking approximation, which is easy to program, gives sufficiently good results for many applications. However, it is known from the study of electron-proton scattering [7] that it starts to significantly overestimate the cross-section when \(\Delta E_{e'} > 10\,\textrm{MeV}\). This can represent an important source of systematic uncertainty when such a simulation is used to estimate the radiative corrections to inelastic electron-nucleus cross-sections. For an adequate description of the radiative tail far away from the elastic line it is crucial to consider cross-section contributions to at least \(e^8\)-order. To achieve this goal, a more sophisticated MC simulation has been devised, which employs an event generator that exactly calculates the coherent sum of the amplitudes for the leading (\(e^3\)-order) diagrams shown in Fig. 1 and then adds next-order contributions as effective corrections to the cross-section.

3.1 Reaction kinematics

In the reaction \({}^{12}\textrm{C} + e \rightarrow {}^{12}\textrm{C} + e' + \gamma \) the initial electron with four-momentum k scatters from the carbon nucleus with the four-momentum p. In the process, a real photon with four-momentum q is produced that leaves the reaction together with the scattered electron (\(k'\)) and the recoiled nucleus (\(p'\)). For the reaction the following four-momentum conservation relation holds:

$$\begin{aligned} k - {k'} -q = {q^*} = {p'} - p, \end{aligned}$$

where \({q^*}\) represents the four-momentum of the virtual photon exchanged between the lepton and the nucleus. We also define four-vectors \(k_1\) and \(k_2\) as the momenta of the internal electron legs:

$$\begin{aligned} k_1 = k - q,\qquad k_2 = {k'} + q. \end{aligned}$$

3.2 Inelastic cross-section

The exclusive cross section for the reaction \({}^{12}\textrm{C} + e \rightarrow {}^{12}\textrm{C}+ e' + \gamma \) in the laboratory frame (LAB) can be written as [24]:

$$\begin{aligned} d\sigma= & {} \frac{\overline{|M_{fi} |^2}}{4M_{{}^{12}\textrm{C}} \mid \vec {k}\mid } \frac{d^3\vec {k}'}{(2\pi )^3 2k_0'} \frac{d^3\vec {q}}{(2\pi )^3 2q_0} \frac{d^3 \vec {p}'}{(2\pi )^3 2 p_0' } \\{} & {} \quad \times (2\pi )^4 \delta ^4(p+ k - {p'} - {k'} - q), \end{aligned}$$

where \(\overline{|M_{fi} |^2}\) represents the spin-averaged square of the reaction amplitude and \(M_{{}^{12}\textrm{C}}\) is the mass of the carbon nucleus. Integrating the expression over the three-momentum of the undetected (recoiled) nucleus and considering \(d^3\vec {k}' = |\vec {k}'|k_0' dk_0' d\Omega _{k'}\), one gets the six-fold differential cross-section:

$$\begin{aligned} \frac{d^6\sigma }{dk_0' d\Omega _{k'} dq_0 d\Omega _{q}}{} & {} = \frac{\overline{|M_{fi}|^2}}{32 M_{{}^{12}\textrm{C}}} \frac{1}{(2\pi )^5} \frac{|\vec {k}'|}{|\vec {k}|}|\vec {q}|\nonumber \\{} & {} \quad \times \frac{\delta (p_0 + k_0 - p_0' - k_0' - q_0)}{p_0'}. \end{aligned}$$
(2)

To obtain the inclusive three-fold differential cross-section \({d^3\sigma }/{dk_0' d\Omega _{k'}}\) that can be compared to the experiment in which only the scattered electron is detected, Eq. (2) needs to be integrated over the energy and angles of the emitted real photon. Although the LAB coordinate system, where \(k_0 = E_{e}\) and \(k_0' = E_{e'}\), is the natural system of the experiment, it is more convenient to perform this integration in the center-of-mass coordinate system (CMS). Therefore, the second part of the cross-section calculation including the amplitude is calculated in the CMS, which is defined by the momenta of the real photon and recoiled nucleus as:

$$\begin{aligned} \vec {p'}_{\textrm{CMS}} + \vec {q}_{\textrm{CMS}} = \vec {k}_{\textrm{CMS}} - \vec {k'}_{\textrm{CMS}} + \vec {p}_{\textrm{CMS}} = 0. \end{aligned}$$

To perform the transformations from LAB to CMS, a four-vector \(z \equiv k - k' + p\) is introduced, defining how the CMS coordinate system moves with respect to the LAB system. With z, any four-momentum vector x can be transformed from LAB to CMS by using the Lorentz transformation

$$\begin{aligned} x^\mu _\textrm{CMS} = \Gamma ^\mu _\nu x^\nu _{\textrm{LAB}}, \qquad \Gamma ^\mu _\nu = \left( \begin{array}{cc} \gamma &{} -\gamma \vec {\beta }^T \\ -\gamma \vec {\beta } &{} 1 + \frac{\gamma -1}{\beta ^2}\vec {\beta }\vec {\beta }^T \end{array} \right) , \end{aligned}$$

where \(\vec \beta \) is the relative velocity of the CMS, \(\vec \beta = \vec {z} / z^0\) and \(\gamma = 1/\sqrt{1-\beta ^2}\). Considering that in the CMS the \(\delta \)-function can be written as:

$$\begin{aligned} \delta (p_0 + k_0 - p_0' - k_0' - q_0) = \underbrace{\frac{p_0'}{q_0 + p_0'}\delta (|\vec {q}|- |\vec {p}'|)}_{\textrm{CMS}}, \end{aligned}$$

the cross-section (2) transforms into:

$$\begin{aligned} \frac{d^3\sigma }{ dk_0' d\Omega _{k'} }{} & {} = \frac{1}{32 (2\pi )^5 M_{{}^{12}\textrm{C}}} \frac{|\vec {k}'|}{|\vec {k}|} \\{} & {} \quad \times \underbrace{\int \int \overline{|M_{fi}|^2}~|\vec {q}|\frac{p_0'}{q_0 + p_0'}\frac{\delta (|\vec {q}|- |\vec {p}'|)}{p_0'} d\Omega _{q} dq_0}_{\mathrm {Calculated~in~CMS}}. \end{aligned}$$

Integrating this formula over the energy of the emitted photon and introducing the Mandelstam invariant \(s = (k-k' + p)^2 = (p' + q)^2 = z^2\), one obtains the following expression for the cross section:

$$\begin{aligned} \frac{d^3\sigma }{ dk_0' d\Omega _{k'}}{} & {} = \frac{1}{64 (2\pi )^5 M_{{}^{12}\textrm{C}}}\frac{|\vec {k}'|}{|\vec {k}|} \\{} & {} \times \underbrace{\int \overline{|M_{fi}|^2}\frac{s - M_{{}^{12}\textrm{C}}^2}{s} d\Omega _{q}}_{\mathrm {Calculated~in~CMS}} . \end{aligned}$$

The following relations, valid in the CMS, were considered:

$$\begin{aligned}{} & {} s = \left( p_0' + q_0 \right) ^2 - (\vec {p}' + \vec {q})^2 = \left( p_0' + q_0 \right) ^2,\\{} & {} s = M_{{}^{12}\textrm{C}}^2 + 2p_0'q_0 - 2\vec {p}'\cdot \vec {q} = M_{{}^{12}\textrm{C}}^2 + 2q_0(q_0 + p_0),\\{} & {} \quad \frac{|\vec {q}|}{q_0+ p_0'} = \frac{q_0(q_0 + p_0')}{(q_0 + p_0')^2} = \frac{s-M_{{}^{12}\textrm{C}}^2}{2s}. \end{aligned}$$

The integration over the solid angle is performed by means of the MC simulation itself. However, the simulation typically generates photon angles in the LAB system, while the integration requires angles in the CMS. Hence, a Jacobian is needed that relates \((\Delta \Omega _q)_{\textrm{LAB}}\) to \((\Delta \Omega _q)_{\textrm{CMS}}\):

$$\begin{aligned} (\Delta \Omega _q)_{\textrm{CMS}} = \frac{(\partial \Omega _q)_{\textrm{CMS}}}{(\partial \Omega _q)_{\textrm{LAB}}} (\Delta \Omega _q)_{\textrm{LAB}}. \end{aligned}$$
(3)

This transformation can be implemented by using the following approximation. First, we define the vectors \(\vec {a}_\textrm{LAB}\) and \(\vec {b}_\textrm{LAB}\) of length \(\epsilon \approx 10^{-7}\) in LAB that are perpendicular to \(\vec {q}\) and perpendicular to each other. Then we transform these two vectors to CMS, obtaining \(\vec {a}_\textrm{CMS}\) and \(\vec {b}_\textrm{CMS}\). The ratio between the areas determined by these new vectors in both coordinate systems gives us the estimate for the Jacobian:

$$\begin{aligned} \frac{(\partial \Omega _q)_{\textrm{CMS}}}{(\partial \Omega _q)_{\textrm{LAB}}} \approx \frac{dS_{\textrm{CMS}}}{dS_{\textrm{LAB}}} = \frac{|\vec {a}_\textrm{CMS}\times \vec {b}_\textrm{CMS}|}{|\vec {a}_\textrm{LAB}\times \vec {b}_\textrm{LAB}|}. \end{aligned}$$

The inclusive cross section for \({}^{12}\textrm{C} + e \rightarrow {}^{12}\textrm{C}+ e' + \gamma \), which depends only on the three-momentum of the scattered electron, and is integrated over \(d\Omega _q\) in the LAB coordinate system, then equals:

$$\begin{aligned} \frac{d^3\sigma }{ dk_0' d\Omega _{k'} }= & {} \int d\Omega _{q} \frac{\overline{|M_{fi}|^2}}{64 (2\pi )^5 M_{{}^{12}\textrm{C}}}\frac{|\vec {k}'|}{|\vec {k}|} \left( \frac{s - M_{{}^{12}\textrm{C}}^2}{s}\right) \nonumber \\{} & {} \times \frac{|\vec {a}_\textrm{CMS}\times \vec {b}_\textrm{CMS}|}{|\vec {a}_\textrm{LAB}\times \vec {b}_\textrm{LAB}|} . {} \end{aligned}$$
(4)

3.3 Amplitude for \({}^{12}\textrm{C} + e \rightarrow {}^{12}\textrm{C}+ e' + \gamma \)

The amplitudes for the Bethe-Heitler diagrams shown in Fig. 1 can be written as:

where and \(Z_{{}^{12}\textrm{C}} = 6\) is the charge number of \({}^{12}\textrm{C}\). The terms in the square brackets represent the electron and carbon currents together with the electron and nucleus vertex factors, respectively. We consider that the electron is a spin-1/2 particle, while the carbon nucleus is spinless. Here \(e_0\) is the elementary charge, while \(F(-{q^{*}}^2)\) represents the nuclear charge form-factor. The terms correspond to internal electron propagators with momentum \(k_i\), while \(\frac{-ig_{\nu \kappa }}{{q*}^2}\) is the virtual photon propagator. The Dirac bispinors u and \({\overline{u}}\) correspond to incoming and outgoing fermions with spin \(s,s'=\uparrow ,\downarrow \). The two particle states can be written as:

$$\begin{aligned}{} & {} u_{\uparrow }(k) = \sqrt{k_0+m_e} \left( \begin{array}{c} 1 \\ 0 \\ \frac{k_z}{k_0+m_e} \\ \frac{k_x + ik_y}{k_0+m_e} \end{array} \right) , \\{} & {} u_{\downarrow }(k) = \sqrt{k_0+m_e} \left( \begin{array}{c} 0 \\ 1 \\ \frac{k_x - ik_y}{k_0+m_e}\\ -\frac{k_z}{k_0+m_e} \end{array} \right) , \end{aligned}$$

with the normalization \({\overline{u}}_s u_{s'} = 2k_0\delta _{s,s'}\).

It needs to be stressed that in general the calculation of the one-photon emission amplitude should involve also Feynman diagrams where the carbon nucleus itself emits a real photon before or after the interaction with the electron. However, with respect to the Bethe-Heitler processes, these diagrams are suppressed by approximately \(k^2/M_{{}^{12}\textrm{C}}^2 \approx 10^{-4}\) and can thus be neglected.

3.4 Carbon charge form-factor

The elastic interaction of electrons with spinless carbon nuclei through the exchange of virtual photons is governed by the charge form-factor \(F(Q^2)\), which carries information about the charge distribution inside the nucleus. Various parameterizations of its charge distribution and form-factor are available for carbon. In this work we considered the parameterization of Hofstadter [25],

$$\begin{aligned} F(Q^2) = \left[ 1- \frac{\beta a^2Q^2 }{2k^2(2+3\beta )} \right] \exp {\left( -\frac{a^2Q^2}{4k^2}\right) }, \end{aligned}$$
(5)

where \(k = \sqrt{3(2+5\beta )/2(2+3\beta )}\), \(\beta = 4/3\) and \(a = 2.4\,\textrm{fm}\) are the parameters of the model [25]. With the exception of the region around the diffraction minimum at \(Q^2 = 0.13\,\mathrm {GeV^2}/c^2\) the model describes the data [26] reasonably well, with the relative precision better than \(10\,\mathrm {\%}\) at \(Q^2<0.35\,\mathrm {GeV^2}/c^2\). In the region of interest, \(Q^2<0.003\,\mathrm {GeV^2}/c^2\), the agreement between the data and model is at the level of \(0.5\,\mathrm {\%}\), see Fig. 2.

Fig. 2
figure 2

Hofstadter’s parameterisation [25] of the carbon charge form-factor, \(F(Q^2)\), superimposed on the existing measurements of Cardman et al. [26]

Full size image

3.5 The spin-averaged square amplitude

The calculation of the spin-averaged square amplitude, \(\overline{|M_{fi} |^2}\), is performed in several steps. In the first step a summation over the index \(\mu \) is performed. For given spin states of electrons, the following sum is calculated:

$$\begin{aligned} M_{fi}^\nu= & {} \frac{-ie_0^3}{{q^*}^2} \sum _\mu {\overline{u}}_{s'}(k') \mathrm {\Xi _e}^{\nu \mu }u_s(k)\> g_{\mu \mu }\> (p+p')_\mu , \end{aligned}$$

where we have considered that \((p+p')^{\kappa }g_{\kappa \mu } = (p+p')_{\mu }\) and we have written the leptonic transition tensor as:

(6)

In the next step, the square of the amplitude is calculated and summation over indices \(\nu \) and \(\nu '\) is performed. Considering also polarization vectors of the emitted photon and summing over all its possible polarization states \(\lambda \), the following relation holds:

$$\begin{aligned} |M_{fi}|^2= & {} \sum _{\nu }\sum _{\nu '}\sum _\lambda {\epsilon _\nu ^{(\lambda )}}^* {\epsilon _{\nu '}^{(\lambda )}} M_{fi}^{\nu }{M_{fi}^{\nu '}}^* \nonumber \\= & {} -\sum _\nu g_{\nu \nu } M_{fi}^{\nu }{M_{fi}^{\nu }}^*, \end{aligned}$$
(7)

where we considered the completeness relation \(\sum _\lambda {\epsilon _\nu ^{(\lambda )}}^* {\epsilon _{\nu '}^{(\lambda )}} = -g_{\nu \nu '}\). In order to obtain the final value of the spin-averaged square of the amplitude, Eq. (7) must be averaged over possible spin states s of the initial electron and summed over possible spin states \(s'\) of the scattered electron:

$$\begin{aligned} \overline{|M_{fi} |^2} = \overline{\sum _{s=\uparrow ,\downarrow }} \sum _{s'=\uparrow ,\downarrow } |M_{fi}|^2 . \end{aligned}$$
(8)

The second summation over the spin states of the final lepton is done explicitly. Averaging over the spin states of the initial electrons, on the other hand, is achieved by randomly generating spins of the initial electrons for each process within the MC simulation.

3.6 Generating random events

The derived formalism can now be used to construct the event generator. In order for the simulation to work, we need to randomly generate four-vectors k, \(k'\) and q (in the LAB frame) for each simulated event. For that purpose we first select the direction and energy of the incident electrons. Traditionally the beam of electrons is pointing along the z-axis of the LAB coordinate system, hence, \(k=(E_e,0,0,\sqrt{E_e^2-m_e^2})\). In the next step, spherical angles \(\theta _{e'}\) and \(\phi _{e'}\) of the scattered electron are randomly generated. They are uniformly distributed over the (spherical) angular acceptance of the spectrometer (detector). Once the direction of the scattered electron is known, its maximal (elastic) energy can be determined by using energy and momentum conservation:

$$\begin{aligned} E_{e'}^{\textrm{elastic}}= & {} \frac{(-E_{e} - M_{{}^{12}\textrm{C}})(E_{e}M_{{}^{12}\textrm{C}} + m_{e}^2)}{(E_{e}^2 - m_e^2)\cos ^2\theta _{e'} - (E_{e}+M_{{}^{12}\textrm{C}})^2} \\{} & {} - \frac{\sqrt{(E_{e}^2 - m_e^2)^2\cos ^2\theta _{e'} \left[ M_{{}^{12}\textrm{C}}^2 - \frac{1}{2}m_e^2(1-\cos 2\theta )\right] }}{(E_{e}^2 - m_e^2)\cos ^2\theta _{e'} - (E_{e}+M_{{}^{12}\textrm{C}})^2}. \end{aligned}$$

In the next step we generate the energy loss of the scattered electron, \(\Delta E_{e'} \in [0, E_{e'}^{\textrm{elastic}}]\), and calculate the energy of the detected electron, \(E_{e'} = E_{e'}^{\textrm{elastic}} - \Delta E_{e'}\). The corresponding four-momentum vector of the scattered electron is then:

$$\begin{aligned}{} & {} k' = (E_{e'},\vec {k}), \\{} & {} \vec {k'} = |\vec {k'}|(\sin \theta _{e'}\cos \phi _{e'}, \sin \theta _{e'}\sin \phi _{e'},\cos \theta _{e'}), \\{} & {} |\vec {k'}|= \sqrt{E_{e'}^2 - m_{e}^2}. \end{aligned}$$

Finally, we generate the emitted real photon. First we determine its direction \(\vec {q} / |\vec {q}|\) by randomly choosing its spherical angles \(\cos \theta _q \in [-1,1]\) and \(\phi _q\in [0,2\pi )\). Then, in the LAB system, where the initial carbon nucleus is at rest, \(p =(M_{{}^{12}\textrm{C}},\vec {0})\), the magnitude of the momentum of the real photon \(|\vec {q}|\) can be determined by using

$$\begin{aligned} |\vec {q}|= \frac{{\vec {q^*}}^2 - {q^*_0}^2 - 2q^*_0 M_{{}^{12}\textrm{C}}}{2\left( -q^*_0 - M_{{}^{12}\textrm{C}} + \vec {q^*} \cdot \frac{ \vec {q}}{ \mid \vec {q}\mid }\right) }. \end{aligned}$$

3.7 Priority sampling

The generated energy-losses of the electron \(\Delta E_{e'}\) should in principle be uniformly distributed on \([0, E_{e'}^{\textrm{elastic}}]\). Similarly, the directions of the emitted photon, given by \((\theta _q,\phi _q)\), should uniformly cover the \(4\pi \) solid angle. In this case the weight of each event in the simulated histograms is determined by the corresponding cross-section. However, such a procedure is very inefficient and would require huge samples of events in order to generate presentable distributions of physically interesting quantities, for instance, the distribution of scattering angle \(\theta _{e'}\) at a chosen value of \(E_{e'}\).

From Eq. (A4) we know that the energy loss of the electron behaves roughly as \(\eta ^a 2a/\Delta E_{e'}\cdot (\Delta E_{e'}/E_{e'}^\textrm{elastic})^{2a}\). Hence, we can use the prescription (B7) to generate energy losses more efficiently and then divide out the approximate distribution (A4) when calculating the weight (cross-section) of each generated event.

Similarly, we know that the probability for emission of a real photon depends strongly on its direction. The most probable directions are along the incident and scattered electron. The probability for emission of a photon then drops rapidly when moving away from these two principal directions, which means that a random generator that distributes photons uniformly over \(4\pi \) would make the simulation very inefficient. Therefore, we rather generate photon angles according to a distribution that mimics the Bethe-Heitler cross-section. Assuming that the photon is emitted from the incoming and the outgoing electron with equal probabilities, the approximate Bethe-Heitler cross section (ABH) can be written as [27]:

$$\begin{aligned} \left( \frac{d\sigma }{d\Omega }\right) _{\textrm{ABH}} = \frac{1}{2} \left( \frac{d\sigma }{d\Omega }\right) _{e} + \frac{1}{2} \left( \frac{d\sigma }{d\Omega }\right) _{e'}, \end{aligned}$$

where contributions from both the incident and the scattered electron can be expressed as:

$$\begin{aligned}{} & {} \left( \frac{d\sigma }{d\Omega }\right) _{x} = \frac{1}{N(E_x, \vec {x})} \frac{1-\cos ^2\theta _{x\gamma }}{\left( \frac{E_{x}}{|\vec {x}|} - \cos \theta _{x\gamma } \right) ^2},\nonumber \\{} & {} N(E_x, \vec {x}) = -4 -2\frac{E_x}{|\vec {x}|}\ln \left( \frac{\frac{E_x}{|\vec {x}|} -1}{\frac{E_x}{|\vec {x}|} +1} \right) . \end{aligned}$$
(9)

Here \(\vec {e}=\vec {k}\), \(\vec {e'}=\vec {k'}\) and \(\theta _{x\gamma }\) is the polar angle between the emitted photon and one of the electrons. A random generator for \(\theta _{x\gamma }\) that distributes angles according to (9), can be implemented as

$$\begin{aligned} \theta _{x\gamma } = F^{-1}(r), \end{aligned}$$

where r is random number uniformly distributed on [0, 1], and \(F^{-1}(r)\) is the inverse of the cumulative function \(F(\theta _{x\gamma })\) of the distribution (9), which can be calculated as:

$$\begin{aligned} F(\theta _{x\gamma })= & {} \int _{-1}^{\cos {\theta _{x\gamma }}}\left( \frac{d\sigma }{d\Omega }\right) _x d\cos \theta \\= & {} \frac{1}{N(E_x, \vec {x})}\left[ \frac{1 - \left( \frac{E_x}{|\vec {x}|}\right) ^2}{\frac{E_x}{|\vec {x}|} - \cos \theta _{x\gamma }} - \cos \theta _{x\gamma } \right. \\{} & {} \quad -\left. 2 \frac{E_x}{|\vec {x}|} \ln \frac{\frac{E_x}{|\vec {x}|}-\cos \theta _{x\gamma }}{\frac{E_x}{|\vec {x}|}+1}-2 + \frac{E_x}{|\vec {x}|} \right] . \end{aligned}$$

The approximate Bethe-Heitler distribution (9) must be divided out before the calculation of the final cross-section, by multiplying the weight of each generated event with \(\left( d\sigma /d\Omega \right) _{\textrm{ABH}}^{-1} \). The cross-section (9) does not depend on the azimuthal angle \(\phi _{x\gamma } \in [0, 2\pi ]\), hence, \(\phi _{x\gamma }\) can be generated by using the standard uniform random generator:

$$\begin{aligned} \phi _{x\gamma } = 2\pi r, \qquad r\in [0,1]. \end{aligned}$$
(10)

3.8 Higher order corrections

In order for the event generator to realistically describe the radiative tail underneath the inelastic electron-nucleus cross-section measurements, higher-order corrections are considered next to the leading order Bethe-Heitler processes by using the formalism of Ref. [7]. The next order vacuum polarization diagrams (with electrons inside the fermion loop) are exactly calculated and are added as a multiplicative factor to the cross section. The virtual corrections to the Bethe-Heitler diagrams (self-energy corrections and various vertex corrections) require integration of the loop diagrams and are computationally too intensive to be considered in the simulation on an event-by-event basis. Instead they are considered as effective corrections to the cross section. The real second-order corrections (emission of the secondary real photon) are considered in the soft-photon limit, which leads to the same multiplicative correction factor \(\delta _R\) as for the elastic case presented in Appendix A.

3.9 The limit \(q_0 \rightarrow 0\)

By considering the relation \(k_i^2 - m_e^2 = -2k_i\cdot q\) in the internal fermion propagators of Eq. (6), one sees that when \(q_0 \rightarrow 0\) each of the propagators introduces a \(1/q_0^2\) divergence of the cross-section. To avoid this divergence in the generator and ensure numerically stable calculation of the cross-section for very small \(q_0\), the \(q_0^2\) is divided out from the amplitude. In the calculation of Eq. (8) we consider only the direction of the real photon \(\frac{\vec {q}}{|\vec {q} |}\). The energy of the real photon is then reintroduced and considered in Eq. (4) when calculating the weight for a given simulated event. In this step we also divide out the term \(\frac{a}{\Delta E_{e'}}\) of the distribution (B6) to compensate for the priority sampling. Since \(\Delta E_{e'}/q_0 \sim 1\) this additional multiplicative factor lowers the power of \(q_0\)-divergence from two to one. Hence, only the term \(\frac{1}{q_0} \propto \frac{1}{\Delta E_{e'}}\) remains in Eq. (4), which results in the correct logarithmic divergence of the integrated cross section given by (1) and (A2). The second part of distribution (B6), \(\left( \frac{\Delta E_{e'}}{E_{e'}^\textrm{elastic}} \right) ^{2a}\), is left in the cross-section (4) and is used together with the factor \(\eta ^a\) to account for the higher-order real-photon corrections in the soft-photon limit, as discussed in Sect. 3.8.

4 Experiment

The measurement of the radiative tail has been performed at the Mainz Microtron (MAMI) in 2013 during the ISR experiment [11] using the spectrometer setup of the A1-Collaboration [28]. In the experiment a point-like electron beam with energy of \(E_{e} = 195\,\textrm{MeV}\) was used in combination with a solid carbon target with surface density of \(92\,\mathrm {mg/cm}^2\). For the cross-section measurements the single-dipole magnetic spectrometer B was employed. It was positioned at a fixed angle of \(\theta _{e'}=15.21^\circ \), while its momentum settings were adjusted to scan the complete radiative tail on the energy range between \(E_{e'} = 40\,\textrm{MeV}\) and \(195\,\textrm{MeV}\). The central momentum of each of the 19 settings was measured with an NMR probe to a relative accuracy of \(8\times 10^{-5}\). The spectrometer was equipped with a detector package consisting of two layers of vertical drift chambers (VDCs) for tracking, two layers of scintillation detectors for triggering, and a threshold Cherenkov detector for identification of electrons and cosmic background suppression.

The beam current was between \(10\,\textrm{nA}\) and \(1\,\mu \textrm{A}\) and was limited by the maximum rate allowed in the VDCs (\(\approx 1\,\mathrm {kHz/wire}\)), resulting in raw rates up to \(20\,\textrm{kHz}\). The current was determined by a non-invasive fluxgate-magnetometer and from the collected charge of the stopped beam.

5 Data analysis

The measured cross-sections were used to validate the new Monte-Carlo generator of radiative correction for electron-carbon scattering. The tests were performed at energies of scattered electrons \(E_{e'}\) that are up to \(150\,\textrm{MeV}\) away from the elastic configuration.

Before comparing the data to the simulation, the measured spectra had to be corrected for the inefficiencies of the detection system. The efficiencies of the scintillation detectors and the Cherenkov detector were determined to be \((99.8\pm 0.2)\%\) and \((99.74\pm 0.02){\%}\), respectively, and were considered as multiplicative correction factors to the measured distributions. The quality of the agreement between the data and simulation depends also on the momentum and spatial resolutions of the spectrometer. The relative momentum plus angular and vertex resolutions (FWHM) were determined to be \(1.7\times 10^{-4}\), \(3\,\textrm{msr}\), and \(1.6\,\textrm{mm}\), respectively.

A series of cuts were applied to the data in order to minimize the background. First, a cut on the Cherenkov signal was applied to identify electrons, followed by a cut on the nominal momentum and angular acceptance of the spectrometer to remove distortions caused by the inefficiencies at the edges of the detectors. At the end a \(\pm 10\,\textrm{mm}\) cut on the vertex position was applied to remove contributions of the events that entered the spectrometer’s acceptance by rescattering from the metal entrance flange of the spectrometer. Since these events have wrong scattering angles, they (virtually) appear in the spectra at large vertex positions and can be efficiently removed with the applied cut on the vertex position.

Additionally, the external radiative corrections in the target material were considered using the formalism of Mo and Tsai [4], while the collisional corrections were approximated by the Landau distribution [29]. The relative uncertainty of the corrections applied to the cross-sections was estimated to be smaller than \(1\,\%\) [4].

The cleaned event samples for each kinematic setting were corrected for dead-time and prescale factors, weighted by the luminosity (determined from the beam current and target density) and then finally merged together to form a single spectrum for the comparison with the simulation.

To simulate the acceptance-averaged cross-sections we embedded the developed event generator into the standard simulation package of the A1 Collaboration, which includes a detailed description of the experimental apparatus [28]. For each kinematic configuration the simulation was run for \(2\cdot 10^8\) events. The obtained distributions for \(\Delta E_{e'}\) and \(\theta _{e'}\) at various \(E_{e'}\) are presented in Figs. 3 and  4.

Fig. 3
figure 3

Comparison of the data to the simulations. Top: The measured cross-section for inelastic scattering of electrons off carbon (black circles) for beam energy \(195\,\textrm{MeV}\) and scattering angle \(15.2\,\mathrm {{}^\circ }\) together with the corresponding peaking approximation (blue line) and the detailed simulation discussed in this work (red line). A small peak at \(172\,\textrm{MeV}\) corresponds to the contribution of the giant resonance [21, 30] to the measured spectrum. Bottom: Relative differences between the data and simulations at various energies of scattered electron \(E_{e'}\). The blue points represent the comparison with the peaking approximation, while the red points correspond to the results for the newly developed detailed simulation. The gray band denotes the region where the relative difference between the data and the simulation is smaller than \(\pm 10\%\). Only statistical uncertainties are shown. The total systematic uncertainty (data+simulation) is estimated to be \(1.2\%\)

Full size image
Fig. 4
figure 4

The cross-sections for electron-carbon scattering as a function of scattering angle \(\theta _{e'}\) at different values of energy of the detected electron \(E_{e'}\). The measurements (black points) are presented together with the simulation based on the peaking approximation (blue line) and the detailed simulation presented in this work (red line)

Full size image

The relative statistical uncertainty of the collected data is \(1.5\%\) for every energy bin. This uncertainty needs to be considered together with the corresponding systematic uncertainty. Although the experiment provided a remarkable control over the systematic uncertainties [12], a few ambiguities remain and limit the precision of the comparison. These include: the experimental uncertainty related to the determination of the luminosity and detector efficiencies (\(\le 0.3\%\)); the contribution of higher-order corrections \((0.4\%)\); the uncertainty of the form-factor model (\(1\%\)); the uncertainty due to the omission of carbon pole diagrams \((0.03\%)\); use of the formalism of Mo and Tsai [4] to describe external corrections to the cross-section (\(0.24\%\)).

6 Results and conclusions

The new simulation described in Sect. 3 exhibits a very good overall agreement with the data. Figure 3 shows that for \(\Delta E_{e'} \le 20\,\textrm{MeV}\) the relative difference between the data and simulation is \(1\%\). For \(\Delta E_{e'}\) between \(20\,\textrm{MeV}\) and \(150\,\textrm{MeV}\) the agreement between the simulation and the data is at the level of \(10\%\). The peak with the shoulder in the region around \(E_{e'} = 172\,\textrm{MeV}\) can be contributed to the excitation of the giant resonance [21, 30], which is most probably the source of the remaining discrepancy between data and simulation. The measurement of the cross-section \(d\sigma /d\Omega _{e'}dE_{e'}\) was performed at smallest achievable beam energy \(E_{e}\) and smallest reachable scattering angle \(\theta _{e'}\) to minimize the contributions from inelastic scattering processes. However, due to the high precision of the experimental data, inelastic events still appeared in the data.

Figures 3 and  4 also demonstrate that the new generator of events is superior to the traditionally used peaking approximation discussed in Appendix B. At \(E_{e} = 195\,\textrm{MeV}\) the approximation works reliably only for \(\Delta E_{e'}\le 1\,\textrm{MeV}\). For other \(\Delta E_{e'}\) the approximation overestimates the size of the radiative tail. At \(\Delta E_{e'} \approx 10\,\textrm{MeV}\) the discrepancy amounts to \(+10\%\), which then quickly increases to above \(100\%\) at \(\Delta E_{e'} = 50\,\textrm{MeV}\).

The remaining inconsistency between the data and simulation could arise also from the incomplete description of higher-order corrections, predominantly the two real-photon emission diagrams, which are considered in the soft-photon limit [7]. While we estimate the systematic uncertainty of this approximation to be smaller than the systematic uncertainty related to the external radiative corrections, it is possible that the full calculation of the two-photon corrections would further reduce the simulated radiative tail. The state-of-the-art calculations of the radiative corrections to the elastic cross-section [8, 23] already offer precise calculations of two-photon emission processes, but in the form of effective correction factors to the elastic cross-sections, which cannot be used directly in the generators of inelastic events. However, they pave a way for improvements of the presented generator.

In relation to the modern calculations of the radiative corrections to the elastic cross-section, the comparison between the data and simulations can be performed also in terms of the radiative correction factor (1). Figure 5 presents \(\delta \) as a function of the minimal energy of the scattered electron, \(E_{e'}^{\mathrm {min.}}\), that is detected by the spectrometer (\(E_{e'}^{\mathrm {min.}}<E_{e'}\)). The figure again exhibits deficiencies of the peaking approximation, which overestimates \(\delta \) for more than \(5{\%}\) when the momentum acceptance of the detector is larger than \(120\,\textrm{MeV}\). The pure first-order inelastic cross-section calculation given by Eq. (4) also insufficiently describes the experimentally determined values, which clearly demonstrates the need for the inclusion of higher-order radiative corrections. The full calculation agrees nicely with the data. The relative difference between the full calculation and the data is better than \(1.6\%\), where \((0.5\pm 0.1)\%\) is due to the presence of the giant resonance.

Fig. 5
figure 5

The radiative correction factor \(\delta \) as a function of the cut-off energy of the scattered electron \(E_{e'}^{\mathrm {min.}}\). Experimentally determined values shown with black points were obtained through the Eq. (1) assuming parametrization of the form factor given by Eq. (5). The results of the peaking approximation described in Appendix B are presented with the dashed blue line. The first-order Bethe-Heitler cross-section calculations are shown with the magenta dashed-dotted line. The results of the full simulation are presented with the full red line and exhibit a better than \(1.6\%\) agreement with the data

Full size image

To conclude, we presented a new Monte-Carlo generator of events for mimicking QED radiative corrections in electron-carbon scattering process that is based on the exact calculation of first order Bethe-Heitler diagrams. Using a dedicated set of experimental data from MAMI together with the analysis package of the A1 Collaboration, we were able to test the generator and demonstrated that it can be successfully applied in the analyses in which a reliable subtraction of the Bethe-Heitler background caused by the elastic peak is required. With the present generator’s limitations the intensity of the studied inelastic process (e.g. low energy quasi-elastic scattering) should be at least two-times larger than the intensity of the radiative tail underneath.