1 Introduction

Heavy-ion collisions are excellent factory for producing both elementary and composed particles as well as for studying their properties and production mechanism. Since many years efforts of theorists and experimentalists were focused on the investigation of time-space evolution of the quark-gluon plasma (QGP) and production of different species of particles, primarily hadrons (pions, kaons, nucleons, hyperons, etc.) emitted in the collision. At high energies, the velocities of such beam nuclei are close to light velocity thus they are often called ultra-relativistic velocities (URV).

Central collisions are the most interesting in the context of the QGP studies. Plasma is, of course, also produced in more peripheral collisions. In peripheral collisions, the so-called spectators are relatively large and have large moving charge. It was realized relatively late that this charge generates strong quickly changing electromagnetic fields that can influence the trajectories and some observables for charged particles.

Such effects were investigated in previous studies of one of the present authors [1, 2]. On one hand side the EM effects strongly modify the Feynman \(x_F\) spectra of low-\(p_T\) pions, creating a dip for \(\pi ^+\) and an enhancement for \(\pi ^-\) at \(x_F \approx \frac{m_{\pi }}{m_N}\). In [1] a formalism of charged meson evolution in the EM field (electric and magnetic) of fast moving nuclei was developed. Later on, the spectacular effects were confronted with the SPS data [3] confirming the theoretical predictions. The investigation was done for \(^{208}\)Pb+\(^{208}\)Pb at 158 GeV/nucleon energy (\(\sqrt{{s}_{NN}} = \) 17.3 GeV) at CERN Super Proton Synchrotron (SPS) [4]. In [2] the influence of the EM fields on azimuthal flow parameters (\(v_n\)) was studied and confronted in [5] with the RHIC data. It was found that the EM field leads to a split of the directed flow for opposite sign charges. In the initial calculation, a simple model of a single initial creation point of pions was assumed for simplicity. More recently, such a calculation was further developed by taking into account also the time-space evolution of the fireball, treated as a set of firestreaks [6]. The distortions of the \(\pi ^+\) and \(\pi ^-\) distributions allow to discuss the electromagnetic effects of the spectator and charged pions in URV collisions of heavy ions and nicely explain the experimental data. This study was done for non-central collisions where the remaining after collision object, called ’spectator’, loses only a small part of nucleons of the original beam/target nucleus.

The ultra-peripheral collisions of heavy ions (e.g. \(^{208}\)Pb +\(^{208}\)Pb) at ultra-relativistic energies (\(\sqrt{s_{NN}}\ge 5~\)GeV) [7] allow to produce particles in a broad region of impact parameter space, even far from “colliding” nuclei. The nuclei passing near one to each other with ultrarelativistic energies are a source of virtual photons that can collide producing e.g. a pair of leptons. In real current experiments (RHIC, LHC), the luminosity is big enough to observe e.g. \(AA \rightarrow AA\rho ^0\) and \(AA \rightarrow AAe^+e^-\), \(AA \rightarrow AA\mu ^+\mu ^-\) processes. One of the most interesting phenomena is multiple interaction [7, 8] which may lead to the production of more than one lepton pair.

The studies on the creation of positron-electron pairs started in early 1930’ties with a prediction of positron by Dirac [9], experimental discovery of positron by Anderson [10] and works of Breit and Wheeler [11], where they calculated the cross section for the production of such pairs in the collisions of two light quanta. The production of \(e^+e^-\) pairs in nucleus-nucleus collisions, goes back to the work on Bethe, Heitler [12] and Landau, Lifschitz [13] in 1934 . It was Williams who realized [14] that the production of \(e^+ e^-\) pairs is enhanced in the vicinity of the atomic nucleus. An overview of the theoretical investigation of the \(e^+ e^-\) pairs creation in historical context was presented by e.g. Hubbell [15] and a detailed discussion about this process was written by Ruffini et al. [16].

The early analyses were done in the momentum space and therefore did not include all details in the impact parameter space. An example of the calculation where such details are taken into account can be found e.g. in [7, 17]. In ultra-peripheral collision (UPC), the nuclei do not collide without loosing, in principle, any nucleon. However, the electromagnetic interaction induced by fast moving nuclei may cause excitation of the nuclei and subsequent emission of different particles, in particular neutrons [18] that can be measured both at RHIC and at the LHC. Moreover the UPC are responsible not only for Coulomb excitation of the spectator but also for the multiple \(\gamma \gamma \) scattering and production of more than one dielectron pair [8].

New experimental results have shown that the b-space EPA may be not sufficient to describe some observables [19], such as \(p_{t, pair}\) distribution. Very recently experimental results for the semi-central collisions controlled by centrality measurement have shown a strong enhancement at \(p_{t, pair} \sim \) 0 (STAR) [20] and a bump at small acoplanarity (ATLAS) [21, 22]. Inclusion of transverse momentum dependent photon distributions improved the situation [23] but did not give the observed experimentally dependence on impact parameter. Recently several works addressed the issue of impact parameter – transverse momentum correlations [24,25,26,27] for different interesting observables. A full treatment is a bit difficult [28] but gives very good description of the semi-central collision data.

Can the strong EM fields generated at high energies modify the charged lepton distributions? No visible effect was observed for electrons with \(p_T>\) 1 GeV as discussed in [8], where the ALICE distributions were confronted with the b-space equivalent photon approximation (EPA) model. But the electromagnetic effect is expected rather at low transverse momenta. According to our knowledge this topic was not discussed in the literature. The ions, which in ultra-peripheral collisions are highly charged, can interact electromagnetically with charged leptons as it was in the case of pions. Similar effects as observed for pions may be expected also for charged leptons. The motion of particles in EM field depends not only on their charge but also on their mass. Thus the distortions of \(e^+/e^-\) or \(\mu ^+/\mu ^-\) distributions should be different than those for \(\pi ^+/\pi ^-\) distributions. Also, the mechanism of production is completely different. In contrast to pion production, where the emission site is relatively well localized, the electron-positron or \(\mu ^+/\mu ^-\) pairs produced by photon-photon fusion can be produced in a broad configuration space around the “collision” point - point of the closest approach of nuclei. For electrons, our model is not as rigorous as it is difficult to justify treating light electrons as localized charges moving in a background EM field. For muons, their heaviness makes our model better justified as their Compton wavelength is smaller. A pedagogical illustration of the impact parameter dependence can be found e.g. in [17].

From one side, the previous works [6] and reference therein, were connected with the electromagnetic effects caused by the emission of the pions from the fireball region. From the other side, the model considered [17, 23, 28] can correctly estimate the localization in the impact parameter space. The present study will be focused on electromagnetic interaction between charged leptons with highly positively charged nuclei.

Our approach consists of two steps. First, the \(e^+ e^-\) and \(\mu ^+/\mu ^-\) distributions are calculated within EPA in a given space point and at a given initial rapidity and transverse momentum. Secondly, the space-time evolution of leptons in the electromagnetic fields of fast moving nuclei with URV is performed by solving relativistic classical equation of motion [29]. In the calculations, we integrate over transverse positions of \(e^+\) or \(e^-\) and \(\mu ^+\) or \(\mu ^-\).

In Sect. 3 the details of the calculation of the differential cross section of \(e^+ e^-\) and \(\mu ^+ \mu ^-\) production will be presented. We will not discuss in detail the equation of motion which was presented e.g. in [29]. The results of the evolution of electrons/positrons in the EM field of “colliding” nuclei are presented in Sect. 4.

2 A comment on quantum multiple-photon exchange effects

The electromagnetic interaction of charged leptons with nuclei was discussed in many contexts in the literature. Very similar to the considered here process is \(\gamma A \rightarrow \ell ^+ \ell ^- A\) reaction. The respective Coulomb effect was discussed e.g. in [30,31,32,33].

The history started with the seminal work of Bethe and Maximon [30]. They discussed the Coulomb effects for bremsstrahlung and dilepton pair production. Tuchin considered [32] multiple \(t-\)channel photon exchanges within the Glauber model. Ivanov and Melnikov [31] presented impact representation of the amplitude for \(e^+ e^-\) photoproduction in the Coulomb field of the nucleus. They wrote leading amplitudes for N t-channel exchanges and showed that in their approximations the amplitudes can be resummed. They calculated corrections to the total \(\gamma A \rightarrow \ell ^+ \ell ^- A\) cross section which is of course much simpler than for differential distributions (not discussed there).

Very recently the Shandong group [33] discussed how to modify the TMD photon distributions in the nucleus due to the strong Coulomb field of the nucleus. This approach may be relevant for \( eA \rightarrow eA\ell ^+ \ell ^-\) at EIC and EicC. Also, this approach is not very useful in our case, where we need rather impact parameter formulation than momentum space formulation.

Very closely related are Coulomb effects in \(\mu + A \rightarrow \mu + A + e^+ e^-\) [34,35,36]. In [35] the authors discuss distributions in \(x = \epsilon _-/\omega \), where \(\epsilon _-\) is electron energy and \(\omega \) is initial photon energy. In a recent paper [36] the authors discuss distributions in \(x = \epsilon _+/\omega \), where \(\epsilon _+\) is positron energy and distribution in muon energy loss through pair production relevant for muons propagating in the atmosphere.

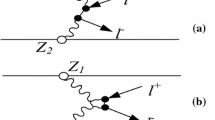
The \(A A \rightarrow A A \ell ^+ \ell ^-\) reaction was also discussed in the literature [37,38,39,40,41,42,43,44,45,46]. In Fig.1 we show an example of the amplitude for a few photon exchanges. It becomes obvious that resummation with exact kinematics and extended charges of nuclei is not easy.

Fig. 1
figure 1

An example of diagrams relevant for multi-photon exchanges

Full size image

The Massachusetts group discussed time-dependent two-center Dirac equation with Coulomb interaction [37, 38]. The papers have a rather technical character. Neither quantitative predictions were given nor differential distributions were discussed.

The Frankfurt group [39] discussed how to modify the impact parameter dependent photon distributions in the strong electromagnetic field of the nuclei. As stated by the authors their approach is not adequate when lepton velocities are similar to the velocity of one of the nuclei. In the present paper, we wish to discuss exactly this region of the phase space. The classical approach performed in [1, 6] for charged pion production in heavy ion collisions suggests that this is the region where spectacular effects may occur.

The authors of [46] reported an explicit calculation of the contribution of exchange of two photons from one nucleus and two photons from the other nucleus. Their results suggest that the familiar eikonalization of Coulomb distortions breaks down. Some relations to \(n \gamma + m \gamma \rightarrow \ell ^+ \ell ^-\) were discussed there. A full formalism is not ready for practical calculations.

The short summary is intended to show that there is no ready formalism which can be used to calculate Coulomb modifications of differential distributions of individual, positively or negatively charged, leptons. Therefore in the following, we suggest to use rather existing classical approach which seems much easier to apply for our purpose. We shall return to the discussion of this approach in the following sections.

3 Lepton pair production, equivalent photon approximation

The particles originated from photon-photon collisions can be created in full space around the excited nucleus thus first of all the geometry of the reaction should be defined. Till recently the b-space EPA [47] was state of the art [48,49,50] for calculating dilepton production cross section, although a slightly different approach, with impact parameter – lepton momentum correlations, was available [51, 52]. Usually, the exclusive dilepton production was estimated by using the monopole charge form factor which allows to reproduce correctly the total cross section. The differential cross sections are more sensitive to details, thus realistic charge form factor (Fourier transform of the charge distribution) has to be employed.Footnote 1 In the b-space EPA (see [47]) the total cross section for \(\ell ^+\ell ^-\) pair production via photon-photon fusion reads

$$\begin{aligned} \sigma= & {} \int \frac{d\omega _1}{\omega _1} \int \frac{d\omega _2}{\omega _2} N\left( \omega _1, {{\textbf {b}}}_1 \right) N\left( \omega _2, {{\textbf {b}}}_2 \right) \Theta \left( b-R_1-R_2 \right) \nonumber \\{} & {} \times 2\pi \int _{R_1}^{\infty } b_1 db_1 \int _{R_2}^{\infty } b_2 db_2 \int _{0}^{2\pi } d \phi \, \sigma _{\gamma \gamma }\left( \omega _1, \omega _2\right) \, .\nonumber \\ \end{aligned}$$
(1)

This can be written in an equivalent way as [17]

$$\begin{aligned}{} & {} \sigma _{AA \rightarrow AA \ell ^+\ell ^-}\nonumber \\{} & {} \quad = \int \frac{\textrm{d} \sigma _{\gamma \gamma \rightarrow \ell ^+\ell ^-} \left( W_{\gamma \gamma }\right) }{\textrm{d}\cos \theta } N\left( \omega _1, {{\textbf {b}}}_1 \right) N\left( \omega _2, {{\textbf {b}}}_2 \right) S^2_{abs}\left( {{\textbf {b}}} \right) \nonumber \\{} & {} \qquad \times 2\pi b \textrm{d} b \textrm{d} {\overline{b}}_x \, \textrm{d} {\overline{b}}_y \frac{W_{\gamma \gamma }}{2} \textrm{d} W_{\gamma \gamma } \, \textrm{d} Y_{\ell ^+\ell ^-} \, {\textrm{d}\cos \theta } \;. \end{aligned}$$
(2)

where \(N(\omega _i, b_i)\) are photon fluxes, \(W_{\gamma \gamma } = M_{\ell ^+\ell ^-}\) is invariant mass and \(Y_{\ell ^+\ell ^-} = (y_{\ell ^+} + y_{\ell ^-})/2\) is rapidity of the outgoing system and \(\theta \) is the scattering angle in the \(\gamma \gamma \rightarrow \ell ^+\ell ^-\) center-of mass system. The gap survival factor \(S^2_{abs}\) assures that only ultra-peripheral reactions are considered. This factor can be calculated e.g. from the Glauber approach [53]. It has interpretation of probability of elastic nucleus-nucleus collision. In the present exploratory calculations we impose an approximate relation \(S^2_{abs}(b) = \Theta (b-R_1-R_2)\), where \(R_1, R_2\) are the radii of colliding nuclei.

The \(\overline{b_x} = (b_{1x}+b_{2x})/2\) and \(\overline{b_y} = (b_{1y}+b_{2y})/2\) quantities are particularly useful for our purposes. We define \(\vec {{{\bar{b}}}} = (\vec {b}_1 + \vec {b}_2)/2\) which is initial position of lepton pair in the impact parameter space. This will be useful when considering the motion of lepton in the EM field of nuclei. The energies of photons are included by the relation: \(\omega _{1, 2} = W_{\gamma \gamma }/2 \exp (\pm Y_{\ell ^+\ell ^-})\). In the following for brevity, we shall use \(b_x, b_y\) instead of \(\overline{b_x}, \overline{b_y}\). Then \((b_x, b_y)\) is the position in the impact parameter plane, where the leptons are createdFootnote 2. The differential (in rapidity and transverse momentum) cross section could be obtained in each emission point in the impact parameter space (\(b_x, b_y\)). The transverse momentum distribution of \(\ell ^+\) or \(\ell ^-\) can be obtained by binning in Eq. (2) \(p_t = p^* \sqrt{1-\cos ^2 \theta }\) where \(p^*\) is lepton momentum in the \(\ell ^+\ell ^-\) center of mass (CM) system. Similar binning is done for \(y_{\ell ^+}\) and \(y_{\ell ^-}\).

The simple b-space EPA formula (2) gives a good description of dilepton invariant mass distributions [7] as measured by the ALICE collaboration [54] for \(p_{t, \ell }>\) 2 GeV. Small electron/positron or \(\mu ^+/\mu ^-\) transverse momenta were not measured so far. In this approach the \(p_{t, pair}\) and acoplanarity distributions are Dirac delta functions. In general, this approach allows to describe rather single lepton distributions (rapidity, transverse momentum). Below we shall compare a transverse momentum distribution of electrons of the b-space EPA with its counterpart for the Wigner-function approach [28] for a given range of impact parameter, relevant for the discussion in the present paper.

Fig. 2
figure 2

The map of differential cross section in rapidity of \(e^+, e^-\) (a) and \(\mu ^+\), \(\mu ^-\) (b) and lepton transverse momentum for (\(b_x, b_y\)) = (0, 0) which will be called CM point for brevity

Full size image

Figure 2 illustrates the differential cross section on the plane of rapidity (y) vs. transverse momentum (\(p_T\)). Rather broad range of rapidity (\(-5, 5\)) is chosen, but the distribution in \(p_T\) will be limited to (0, 0.1 GeV) as the cross section drops at \(p_T\) = 0.1 GeV already a few orders of magnitude. The electromagnetic effects may be substantial only in the region of the small transverse momenta. Thus for our exploratory study here we have limited the range for rapidity to (\(-5, 5\)) and for transverse momentum to \(p_T\) = (0, 0.1 GeV).

The influence of particle mass on the lepton production is well visible as the differential cross section for electrons/positrons is at least six orders of magnitude higher than that for muons. In general, \(p_T\) distributions of heavier leptons are wider.

Can the subtle impact parameter – lepton transverse momentum correlations influence the single lepton transverse momenta? This was not discussed so far in the literature.

Fig. 3
figure 3

Differential cross section for PbPb\(\rightarrow \)PbPb\(e^+e^-\) as a function of \(\log _{10}(p_{t, e})\). Shown are results of different approaches as explained in the figure legend. The left panel shows impact parameter integrated cross section while the right panel is for a narrow range of impact parameter \(b \in (13.95, 14.05)\) fm

Full size image

In Fig. 3 we compare results for the somewhat simplified b-space EPA, the \(k_t\)-factorization approach [23] and the Wigner-function approach [28]. We show results for the full range of impact parameter (left panel) as well as for very limited range discussed in the present paper (right panel). In the latter case, there is no \(k_t\)-factorization result shown in the left panel. We see interesting results for \(p_{t, e}<0.01\) GeV. This region requires dedicated studies in the context of possible measurement with ALICE3 detector. We observe deviations of the b-space EPA result and the Wigner-function approach result for small lepton transverse momenta \(p_t<\) 0.1 GeV. Sizeable numerical fluctuations in the Wigner-function approach can be observed. Since in the present exploratory calculations we are interested rather in estimating the size of the outcome related to the electromagnetic interactions of leptons with the nuclei as well as phase-space localization (rapidity, transverse momentum), in the present paper we wish to use a more handy b-space EPA approach (6-dimensional integration). One has to have in mind that precise evaluation of the low-\(p_t\) distributions requires use of the rather complicated Wigner-function approach (10-dimensional integration). Using the Wigner-function approach together with the inclusion of the final state interaction effects goes beyond the scope of the present paper but would not change the general conclusions drawn here.

The calculations will be done assuming the collision of \(^{208}\)Pb+\(^{208}\)Pb at 158 GeV/nucleon energy (\(\sqrt{{s}_{NN}} = \) 17.3 GeV) corresponding to the CERN SPS and \(\sqrt{{s}_{NN}} = \) 200 GeV of the STAR at RHIC at impact parameter 14 ± 0.05 fm which is approximately twice the radius of the lead nucleus. This is a minimal configuration assuring ultra-peripheral collisions. For comparison also the higher impact parameter (50 ± 0.05) fm is discussed.

Fig. 4
figure 4

The impact parameter space and the five selected points (\(b_x, b_y\)): (0, 0), ( ± 15, 0) fm, (0, ± 15) fm, for which the distribution in rapidity and transverse momentum will be compared latter on in the text, shown in the CM rest frame

Full size image
Fig. 5
figure 5

The differential cross section for various emission points of \(e^{+/-}\) (top row) and \(\mu ^{+/-}\) (bottom row) produced in the \(^{208}\)Pb+\(^{208}\)Pb reaction at 158 GeV/nucleon energy (\(\sqrt{{s}_{NN}} = \) 17.3 GeV) at impact parameter 14 ± 0.05 fm. The cross section for selected points (\(b_x, b_y\)): (0, 0), ( ± 15, 0) fm, (0, ± 15) fm and (40, 0) fm are integrated over \(p_T\) (a, c) and rapidity (b, d), respectively

Full size image

In the present study, the ultra-peripheral collisions are investigated in the reaction plane (\(b_x, b_y\)) which is perpendicular to the beam axis taken as z-direction. The collision point (\(b_x = 0, b_y = 0\)) is time-independent center of mass (CM) of the reaction as shown in Fig. 4. The impact parameter is fixed as a double radius of each (identical) Pb nucleus b = (13.95, 14.05) fm. For comparison, we will show results also for b = (49.95, 50.05) fm. Four characteristic points ( ± 15, 0) fm, (0, ± 15) fm, which are discussed later are also marked in the figure. In the present paper, we shall show results for these emission points for illustrating the effect of the evolution of charged leptons in the EM field of nuclei. Here we wish to present some preliminary results for selected values of impact parameter. The integrated distribution can be seen in Fig. 5a–d. There we compare the distributions obtained for different emission points (\(b_x, b_y\)): (0, 0), ( ± 15, 0) fm, (0, ± 15) fm and (40, 0) fm as shown in Fig. 4. The behavior of the differential cross section is very similar in each (\(b_x, b_y\)) point but it differs in normalization as it is shown in Fig. 5.

The emission point of the leptons does not change the behavior (shape) of the cross section on the (\(y, p_T\)) plane but changes the absolute value of the cross section. As it is visible in Fig. 5a–d the biggest cross section is obtained for the CM emission point. The production of \(e^+, e^-\) but also \(\mu ^+, \mu ^-\) at (\(b_x, b_y\)) = (40, 0) fm i.e. far from the CM point, is hindered by three orders of magnitude.

Moreover, the production at \(b_x = \pm \)15 fm and \(b_y\) = 0 is more preferable than the production at \(b_x\) = 0 and \(b_y\) = ± 15 fm which is fully understandable taking into account the geometry of the system (see Fig. 4). The change of the emission point in \(b_x\) direction is better visible for muons than for electrons (compare the green and the orange lines in rapidity distributions, Fig. 5a). Muons show that the maximum of the cross section is around \(p_T = 0.05\) GeV when electrons are peaked around 0.

Fig. 6
figure 6

Two-dimensional cross section for \(e^+, e^-\) (a, b) and \(\mu ^+\), \(\mu ^-\) (c, d) as a function of \(b_x\) and \(b_y\) for two values of impact parameter: (a, c) b = 14 ± 0.05 fm and (b, d) b = 50 ± 0.05 fm

Full size image

As the system taken here into consideration is fully symmetric (\(A_1 = A_2, Z_1 = Z_2\)), thus corresponding results are symmetric under the following replacements: \(b_x \rightarrow -b_x\) or \(b_y \rightarrow -b_y\). Figure 6 compares the integrated cross section on reaction plane (\(b_x, b_y\)) for two impact parameters: (a, c) b = 14 ± 0.05 fm (when nuclei are close to each other) and (b, d) b = 50 ± 0.05 fm (when nuclei are well separated). Results for electron-positron (top row) and \(\mu ^+/\mu ^-\) production (bottom row) are presented separately. The landscape reflects the position of the nuclei in the moment of the closest approach || it doesn’t depend on the lepton mass. Similar plots have also been done for higher \(\sqrt{s_{NN}}\) but the shape is almost unchanged, only the cross section values are different. This figure illustrates the influence of the geometry of the reaction. Regardless of the impact parameter, the distance between colliding nuclei, the cross section has a maximum at \(b_y = 0\). The increase of b leads to a doubling of the peak in \(b_x\).

Fig. 7
figure 7

Distribution of the cross section in the impact parameter b for different Pb–Pb collision energies: \(\sqrt{s_{NN}}\) = 17.3, 50 and 200 GeV (from bottom to top) for \(e^+e^-\) (a) and \(\mu ^+\mu ^-\) production (b)

Full size image

In Fig. 7 we show a distribution of the cross section in impact parameter b for different collision energies \(\sqrt{s_{NN}}\) = 17.3, 50, 200 GeV. In this calculation, we have taken \(p_T>\) 0 GeV (the cross section strongly depends on the lowest value of lepton transverse momentum \(p_T\)). In general, the larger collision energy the broader range of impact parameter. However, the cross section for \(b \approx R_{1} + R_{2}\) is almost the same. Only taking into account limitation, e.g. on the momentum transfer, makes the difference in the cross section significant even at \(b = 14\) fm. The electrons/positrons impact parameter distributions have almost linear dependence but muons show rather exponential ones for the selected range of impact parameter.

Fig. 8
figure 8

Differential cross section as a function of \(\log _{10}p_T\) for dilepton production in ultraperipheral lead-lead collisions for different energies: \(\sqrt{s_{NN}}\) = 17.3, 50 and 200 GeV (from bottom to top). Results for electron-positron and muon pairs are shown separately

Full size image
Fig. 9
figure 9

The differential cross section for various emission points of electron/positron (a, b) and muons (c, d) in the \(^{208}\)Pb + \(^{208}\)Pb reaction at \(\sqrt{{s}_{NN}} = \) 17.3, 50, 200 GeV at impact parameter 14 ± 0.05 fm

Full size image

Rather small transverse momenta enter such calculation. To illustrate this in Fig. 8 we show a distribution in \(log_{10}(p_T)\). As seen from the figure the cross section is integrable and we have no problem with this in our Monte Carlo routine [55]. The calculations confirm that the shape of the electron/positron distribution, shown in Fig. 9a, b does not depend on the energy of the colliding nuclei. There are visible small differences in the magnitude of cross sections for \(\sqrt{{s}_{NN}} = \) 17.3 and 200 GeV at least in the selected limited \(p_T\) = (0, 0.1) GeV range. Dependence on the rapidity is even weaker as the differences are visible only for \(|y|>\)3. For muons the distributions in rapidity become wider with growing collision energy.

These cross sections are used as weights in the calculation of electromagnetic effects between charged leptons and the fast moving nuclei. The corresponding matrix has following dimensions: \(b_{x, y} = (-50, 50)~\textrm{fm} - 99\times 99\) points in the reaction plane and 100\(\times \)15 in the (\(y, p_T\)) space. Every \(b_{x, y}\) point is probed 1000 times to assure the good randomization of in the (\(y, p_T\)) space.

Any extra electromagnetic interaction, in addition to the production process, may lead to the excitation of the colliding nuclei which is not discussed in the present paper. In general, different types of interaction are possible: excitation of giant resonances, proton/neutron knock-out processes, nucleon excitations, DIS off quarks/antiquarks. Such processes were discussed (also by us) in the context of nucleus excitation [18] and emission of neutrons.

The knock-out processes are interesting in our context as they are relatively fast and change the content of nuclei, potentially also their charge. At not too high energies the strong-interaction initiated knock-out processes were discussed for intermediate-energy processes [56] (see also Ref. [57, 58]). The knock-out processes may be also initiated by electromagnetic processes: coherent emission of photon and/or photons exchanged in nucleon–nucleon interactions. In our opinion, coherent photons are more important in this context. This effect was not discussed separately at high energies. The emission of one or two nucleons is not crucial for our estimates of EM effects for heavy nuclei such as Pb or Au. First of all the probability of such an effect should not be too big.

The \((\gamma , p)\) and \((\gamma , n)\) processes can be calculated using e.g. DWIA method. Also \((\gamma , NN)\) processes due to MEC can be also important. The \((\gamma , pn)\) contribution can be estimated using so-called modified quasi-deuteron approximation. In this case, simple approximations are possible.

4 Electromagnetic interaction effects

It is our aim to study the influence of the strong EM fields generated by nuclei on the distributions of produced muons, separately for \(\mu ^+\) and \(\mu ^-\).

The spectator system is modelled as two uniform spheres in their respective rest frames that change into disks in the overall center-of-mass collision frame. The total charge of nuclei is 82 consistent with UPC. The lepton emission region is reduced to a single point and the time of emission is in general a free parameter.

Fig. 10
figure 10

Rapidity vs \(p_T\) distributions for final (subjected to EM effects) \(\mu ^-\) for different emission points: a (0, 0) and d full xy plane; b (0, 15) fm; c (15, 0) fm; e (0, \(-15\)) fm and f (\(-15\), 0) fm. These results are for \(\sqrt{s_{NN}}\) = 17.3 GeV

Full size image
Fig. 11
figure 11

Rapidity vs \(p_T\) distributions for final (subjected to EM effects) \(\mu ^+\) for different emission points: a (0, 0) and d full xy plane; b (0, 15) fm; c (15, 0) fm; e (0, \(-15\)) fm and f (\(-15\), 0) fm. These results are for \(\sqrt{s_{NN}}\) = 17.3 GeV

Full size image
Fig. 12
figure 12

Reduced rapidity distributions for final \(\mu ^+\) (red) and \(\mu ^-\) (blue) for fixed b and (\(b_x\) = 0, \(b_y\) = 0) plane of emission points at three collision energies: \(\sqrt{s_{NN}}\) = 17.3, 50 and 200 GeV

Full size image

In this work, we assume that there is no delay time between collisions of nuclei and the start of the EM interactions. The z-dependence of the first occurrence of the \(l^+ l^-\) pair is beyond the EPA and is currently not known. In our opinion production of \(\ell ^+ \ell ^-\) happens when the moving cones, fronts of the EM fields, cross each other. This happens for \(z \approx \) 0. In the following, we assume z = 0 for simplicity.Footnote 3

Fig. 13
figure 13

Reduced rapidity distributions for final \(\mu ^+\) (red) and \(\mu ^-\) (blue) for fixed b and full (\(b_x\), \(b_y\)) plane of emission points at three collision energies: \(\sqrt{s_{NN}}\) = 17.3, 50 and 200 GeV

Full size image

Classical and quantal approaches to scattering in the Coulomb field lead to the same differential angular distributions \(d \sigma / d \Omega \). So we expect that the classical (time-dependent) approach may be a reasonable approximation to estimate the EM effects in our very dynamic system. Our initial conditions for the classical physics approach remind those for the \(e^{\pm } A\) scattering. We treat our EPA distributions as initial conditions for the EM interactions. We integrate over initial conditions (position of \(\ell ^{\pm }\) with respect to both highly charged nuclei). The integration in the transverse plane is dictated by the EPA.

The trajectories of \(\ell ^{\pm }\) in the field of moving nuclei are obtained by solving the equation of motion numerically for charged leptons:

$$\begin{aligned} \frac{d \vec {p}_{\ell ^{\pm }}}{d t} = \vec {F}_{1, \ell ^{\pm }}(\vec {r}_1, t) + \vec {F}_{2, \ell ^{\pm }}(\vec {r}_2, t) \; . \end{aligned}$$
(3)

The total interaction is a superposition of interactions with both nuclei which positions depend on time. We solve the motion of charged leptons in the overall center of mass system, i.e. both position and time are given in this frame. In this frame we have to deal with both electric and magnetic force [1]. Because nuclei are very heavy compared to electrons/positron but also to muons their motion is completely independent and is practically not distorted by the EM interaction. We take:

$$\begin{aligned} \vec {r}_1(t)= & {} + {{\hat{z}}} c t + \vec {b}/2 \; , \nonumber \\ \vec {r}_2(t)= & {} - {{\hat{z}}} c t - \vec {b}/2 \; , \end{aligned}$$
(4)

i.e. assume that the nuclei move along straight trajectories independent of the motion of charged leptons. The step of integration depends on energy and must be carefully adjusted.

Fig. 14
figure 14

Transverse momentum distributions for final \(\mu ^+\) (red) and \(\mu ^-\) (blue) for fixed b and full (\(b_x\), \(b_y\)) plane of emission points at three collision energies: \(\sqrt{s_{NN}}\) = 17.3, 50 and 200 GeV

Full size image
Fig. 15
figure 15

The electron and positron (top) and muons (bottom) emission cross section normalized to 100% in the \(^{208}\)Pb+\(^{208}\)Pb reaction at 158 GeV/nucleon energy (\(\sqrt{{s}_{NN}} = 17.3\) GeV) at impact parameter 14 ± 0.05 fm assuming the \(p_T = (0, 0.1)\) GeV produced in the center of mass (0, 0) point (a, c) and when integrating over full reaction space (b, d). Shown are original EPA distributions (dotted line) and results when including evolution in the EM field of nuclei for positrons (solid line) and for electrons (dashed line)

Full size image
Fig. 16
figure 16

Distribution of \(\mu ^-\) (a, c) and \(\mu ^+\) (b, d) for \(\sqrt{s_{NN}}\) = 17.3 GeV at b = 14 fm integrated over (\(b_x, b_y\)) = (−100, 100) fm, \(p_T^{ini}\) = (0, 0.1) GeV

Full size image
Fig. 17
figure 17

Distribution of \(\mu ^-\) (a, c) and \(\mu ^+\) (b, d) for \(\sqrt{s_{NN}}\) = 17.3 GeV at b = 50 fm integrated over (\(b_x, b_y\)) = (\(-100\), 100) fm, \(p_T^{ini}\) = (0, 0.1) GeV

Full size image
Fig. 18
figure 18

Distribution of \(\mu ^-\) (a, c) and \(\mu ^+\) (b, d) for \(\sqrt{s_{NN}}\) = 200 GeV at b = 14 fm integrated over (\(b_x, b_y\)) = (\(-100\), 100) fm for \(p_T^{ini}\) = (0, 0.1) GeV

Full size image

We wish to make a supplementary comment on the applicability of the classical approach used in the present paper. In principle, one could worry about the uncertainty principle. In our calculations, we assume that we know simultaneously momenta and positions of charged leptons. In the region of interest momenta of leptons are not small. Only transverse momenta are small. As shown in our paper, for the EM interactions the exact position is not crucial for final distributions. The effect becomes smaller only when the initial distances are dramatically modified. So we feel the uncertainty principle is not a crucial limitation for our study. In addition, we showed in our earlier calculations for pion production [1, 6] that the dramatic effects for pion velocities close to the velocity of one of the heavy ion beams can be well described by the classical approach.

Combining quantal calculation, which provides an initial condition for the subsequent evolution of trajectories of charged leptons is the only solution how to include the interaction of nuclei with the charged leptons known to us. The fully quantal approach does not exist and we do not know how to construct it.

The quantal calculation provides localization of nuclei and lepton emission points in the impact parameter space. Finally one should do integration over such localizations. In this sense, there is not strict localization. The distribution of the localization points is consistent with the quantal calculation. We cannot add extra ad hoc delocalization as the final result would be easily inconsistent. Since one should integrate over different positions of lepton emission in the impact parameter space we do in practice effective evolution of initial distributions of positively and negatively charged leptons. Such an approach is often done in a classical mechanics approach to quantum mechanics.

In general, the heavier particle (lepton in our case) the better should be the classical calculation. Since the classical treatment is valid for pions, as documented in the literature, we decided to do our calculation for muons rather than for electrons. Muons have the mass very similar to the pion mass so we think that our hybrid approach should be valid in this case. However, we think that our calculation should be reasonable even for electrons as explained above using the argument of localization consistent with EPA.

Our approach could also be used to study the influence on the observables related to the dilepton pair, such as invariant mass or transverse momentum of the pair. Temporary calculation shows that the effect then is much smaller than for individual distributions. Therefore we decided not to discuss this in this paper.

The (rapidity, \(p_T\)) distributions of initial leptons are obtained by randomly choosing the position on the two-dimensional space. The path of a particle in an electromagnetic field generated by nuclei are traced up to 10, 000 fm away from the original interaction point. The Monte Carlo method is used to randomize the initial rapidity and \(p_T\) from the uniform distribution. The initial rapidity and \(p_T\) of charged leptons are randomly chosen in the range: \(y = (-5, 5)\) and \(p_T\) = (0, 0.1) GeV as fixed in the previous section. The (\(y, p_T\)) distributions for final (subjected to the EM evolution) leptons are presented in Figs. 10 and 11. These distributions were obtained by analyzing the EM evolution event-by-event. The number of events taken here is \(n_{event}\) = 10\(^7\) for each two-dimensional plot.

For \(\mu ^-\) (and electron) production an enhancement and for \(\mu ^+\) (and positron) a loss with respect to the neighborhood or/and flat initial distribution is observed for \(y \approx \pm \) 3 which corresponds to the beam rapidity at \(\sqrt{s_{NN}}\) = 17.3 GeV energy.

These two sets of two-dimensional plots illustrate the effect of the EM interaction between \(\ell ^+\) or \(\ell ^-\) and the moving nuclei. The motion of particles in the EM field of nuclei changes the initial conditions and the final (\(y, p_T\)) are slightly different. Figure 10 shows the behavior of \(\mu ^-\) and Fig. 11 of \(\mu ^+\) at CM (a) and different impact parameter points: (panels c, f) ( ± 15, 0) fm and (panels b, e) (0, ± 15) fm marked in Fig. 4. We observe that the maximal number of \(\mu ^-\) is located where the cross section for \(\mu ^+\) has minimum. The Coulomb influence is well visible as a missing area for \(\mu ^+\) for \(p_T<0.02\) GeV for particles emitted from the CM point. The emission of leptons from \(b_y = \pm \)15 fm gives a lower effect. The asymmetry in emission is well visible for \(b_x\) = ± 15 fm, where a larger empty space is for positive rapidity when \(b_x\) = 15 fm and for negative rapidity when \(b_x = -15\) fm.

Although the EM effects are noticeable for \(\mu ^-/\mu ^+\) in different impact parameter points, the integration over the full reaction plane washes out almost totally this effect.

For comparison the results of integration over full space \(b_x = (-50, 50)\) fm and \(b_y = (-50, 50)\) fm are shown in panels (d) of Figs. 10 and 11. These results are independent of the source of leptons, thus it could be treated as a general trend and an indication for which rapidity-transverse momentum ranges one could observe the effects of the EM interaction between charged leptons and nuclei.

The distribution in reduced rapidity of final leptons is shown in Figs. 12 and 13. The reduced rapidity (dimensionless quantity) is the rapidity y normalized to the beam rapidity \(y_{beam}\) (different for various collision energies)

$$\begin{aligned} y_{red} = y / y_{beam} \; , \end{aligned}$$
(5)

where

$$\begin{aligned} y_{beam} = \pm ln \left( \frac{\sqrt{s_{NN}}}{m_p} \right) \end{aligned}$$
(6)

and \(m_p\) is the proton mass. The results shown above were obtained, somewhat arbitrarily, with uniform distribution in \((y, p_T)\). This leads to the observation of peaks or dips at beam rapidities. No such peaks appear for \(\sqrt{s}\) = 200 GeV as here the chosen range of rapidity (\(-5, 5\)) is not sufficient. Whether such effects survive when weighting with the b-space EPA cross section will be discussed below.

Figure 12 is focused on emission from the center of mass point and Fig. 13 is obtained when integrating over full (\(b_x, b_y\)) plane. The main differences between \(\mu ^-\) (blue lines) and \(\mu ^+\) (red lines) distributions are not only at midrapidities but also around the beam rapidity. The effect is more visible for the CM emission point but it is slightly smoothed out when the full \((b_x, b_y)\) plane is taken into consideration. Moreover increasing the impact parameter (panels (a) and (b)) diminishes the difference between rapidity distributions of final \(\mu ^-\) and \(\mu ^+\). The beam energy is another crucial parameter. The collision with \(\sqrt{s_{NN}} > 100\) GeV (panel (d)) does not allow for sizeable effects of electromagnetic interaction between leptons and nuclei, at least at midrapidities.

The discussion of the EM interaction between \(\mu ^+\) or \(\mu ^-\) and nuclei has to be completed by combining with the cross section of lepton production as obtained within EPA. Taking into account the leptons coming from photon-photon fusion the distributions from Figs. 10 and 11 are multiplied by differential cross section obtained with Eq. (2).

The details of the method are presented in Ref. [1] and adapted here by replacing pion emission to muon or electron emission. In Fig. 14 we show the influence of EM interaction on \(p_T\) distributions. Here we integrate over rapidity and (\(b_x, b_y\)). One can observe that the EM effects lead to a diffusion of transverse momenta (see the diffused edge at \(p_T = 0.1\) GeV, marked by a green vertical line). No spectacular influence is observed when changing the impact parameter or beam energy.

Figure 15 shows a comparison of rapidity distribution of final electrons and positrons (top) and muons (bottom), assuming the particles are emitted from the center of mass (0, 0) point (a, c) and when integrating over \(b_x, b_y\) (b, d). The comparison is done between EPA distribution relevant for the initial stage (red, dotted line) with the final stage, resulting from the EM interaction of charged leptons with positively charged nuclei. If leptons are produced in the CM point, the electron distributions are almost unchanged but positron distributions are squeezed to \(|y| < 2\). In contrast, \(\mu ^+\) or \(\mu ^-\) distributions are very similar to each other. If the cross section is integrated over full (\(b_x, b_y\)) parameter space, the positron distribution is still steeper than that for electrons but mainly for \(|y|<\) 2.

Even when the leptons produced in the full (\(b_x, b_y\)) plane are considered, the \(e^+\) and \(e^-\) distributions are different from the initial ones. The electrons and muons are focused at midrapidities under the EM interactions.

The dependence on the position of emission and final rapidity allows to understand how the geometry influences the electromagnetic interaction between leptons and nuclei. Figures 16, 17 and 18 present the cross section distribution in \(b_x\) (top rows) and rapidity for \(\mu ^-\) (a) and \(\mu ^+\) (b) and in \(b_y\) (bottom rows) and rapidity for \(\mu ^-\) (c) and \(\mu ^+\) (d). Figures 16 and 17 are for \(\sqrt{s_{NN}}\) = 17.3 GeV with the impact parameter 14 ± 0.05 fm and 50 ± 0.05 fm. Fig. 18 is for \(\sqrt{s_{NN}}\) = 200 GeV and b = 14 fm. Distributions for \((b_x, y_\mu )\) in Fig. 17 are quite different than those for \((b_y, y_\mu )\). These plots allow to quantify the anisotropy caused by the interaction of leptons of different charge and nuclei. It is more visible for larger impact parameter when the spectators are well separated (Fig. 17).

Fig. 19
figure 19

Rapidity distribution of electrons and positron (top) and muons (bottom) for \(\sqrt{s_{NN}}= 17.3\) GeV (b = 14, 50) fm and 50 GeV and 200 GeV with b = 14 ± 0.05 fm (only) integrated over \((b_x, b_y) = (-50, 50)\) fm, \(p_T^{ini}\) = (0, 0.1) GeV

Full size image
Fig. 20
figure 20

The ratio of rapidity distributions of positrons and electrons (left) and \(\mu ^+/\mu ^-\) (right) for \(\sqrt{s_{NN}}\) = 17.3 GeV and fixed b = 14 fm and 50 fm and \(\sqrt{s_{NN}}\) = 50 GeV and 200 GeV with fixed b = 14 fm integrated over (\(b_x, b_y\)) = \((-50, 50)\) fm and transverse momenta in the interval \(p_T^{ini}\) = (0, 0.1) GeV

Full size image

Distributions for fixed impact parameter and different beam energies reflect the behavior seen in Fig. 13. For collision with \(\sqrt{s_{NN}}\) = 200 GeV (Fig. 18) the muons almost do not feel the presence of the EM fields of the nuclei.

Integrating over full (\(b_x, b_y\)) plane one obtains the rapidity distribution of final leptons shown in Fig. 19 separately for electrons (a), positrons (b), \(\mu ^-\) (c) and \(\mu ^+\) (d) for two impact parameters: 14 fm (dashed lines) and 50 fm (full lines). Electrons have a somewhat wider distribution than positrons and this is independent of the impact parameter. Positively and negatively charged muon distributions look very similar. While positron rapidity distributions only weakly depend on collision energy it is not the case for electrons, where sizeable differences can be observed (Fig. 19).

The ratio of distributions for positrons and electrons (Fig. 20) reflects the behaviour seen in Figs. 16 and 17. This plot shows a combined effect of EPA cross section and the EM interactions of leptons with nuclei. Thus despite the production cross section is lower for larger impact parameter, the discussed phenomenon should be visible for larger rapidities. The ratio quickly changes with energy and tends to 1 for larger energies (see dotted line for \(\sqrt{{s}_{NN}}\) = 200 GeV). The influence of EM interaction on muon distributions is much smaller than for electron distributions. This is because very small transverse momenta are populated for electrons/positrons but not for \(\mu ^+/\mu ^-\).

5 Conclusions

In the last 15 years the electromagnetic effects due to a large (moving) charge of the spectators on charged pion momentum distributions were observed both in theoretical calculations and experimentally in peripheral heavy ion collisions at SPS and RHIC energies. Interesting and sometimes spectacular effects were identified.

In the present paper, we have discussed whether such effects could also be observed for the distributions of charged leptons produced via photon-photon fusion in heavy ion UPCs. The corresponding cross section can be rather reliably calculated and turned out to be large, especially for low transverse momentum electrons/positrons or \(\mu ^+/\mu ^-\). The impact parameter equivalent photon approximation is well suitable for investigating the electromagnetic effects. On the experimental side only rather large transverse momentum electrons/positrons could be measured so far at RHIC and the LHC, typically larger than 0.5 GeV.

We have organized calculations that include the EM effects using as input EPA distributions. First, multi-differential (in momenta and impact parameter) distributions for the diphoton production of the \(e^+ e^-\) and \(\mu ^+\mu ^-\) pairs are prepared in the impact parameter equivalent photon approximation. Such distributions are used next to calculate the propagation of the electrons/positrons or \(\mu ^+/\mu ^-\) in strong EM fields generated by the quickly moving nuclei. The propagation has been done by solving numerically relativistic equation of motion. Strong EM effects have been observed only at very small transverse momenta of electron/positron or \(\mu ^+/\mu ^-\). Therefore to accelerate calculations we have limited to really small initial transverse momenta \(p_T<\) 0.1 GeV.

The shape of the differential cross section in rapidity and transverse momentum does not depend on the energy of the process but rather on the emission point in the impact parameter plane (\(b_x, b_y\)). We have investigated effects for different initial conditions, i.e. different emission positions in the impact parameter space.

The leptons produced in photon-photon fusion interact electromagnetically with charged nuclei which changes their trajectories. The biggest effect has been identified for the CM emission point. However, the integration over full (\(b_x, b_y\)) plane washes out this effect to large extent. The range of \(p_T\) = (0, 0.02) GeV has turned out the most preferable to investigate the influence of the EM effects on leptons originating from various (\(b_x, b_y\)) plane points.

Moreover, the initial position in the impact parameter space influences not only the value of the cross section but also the shapes of distributions of final leptons.

The \(AA \rightarrow AA\ell ^+\ell ^-\) process creates leptons in a broad range of rapidities. We have found that only at small transverse momenta of electrons/positrons or \(\mu ^+/\mu ^-\) one can observe sizeable EM effects.

The performed calculations allow to conclude that the maximal beam energy for the Pb+Pb collision, where the EM effects between leptons and nuclei are evident at midrapidities, is probably \(\sqrt{{s}_{NN}}\) = 100 GeV. Observation of this outcome at higher energies may be therefore rather difficult, if not impossible. The effect survives even at high energies but close to beam rapidity. However, this region of the phase space is usually not instrumented and does not allow electron/positron or \(\mu ^+/\mu ^-\) measurement.

So far the effect of EM interaction was studied for fixed values of the impact parameter (mainly for b = 14 fm). However, the impact parameter cannot be measured. The integration over the impact parameter is rather difficult and goes beyond the scope of the present paper. Such integration will be studied elsewhere. It was shown recently [23, 28] that the \(\gamma \gamma \) fusion production of \(\ell ^+\ell ^-\) pairs survives even in semicentral collisions and constitutes important contributions at very peripheral collisions. Then the numerical integration over a limited range of b would be possible even at present. On the experimental side one could show results, both distributions for electrons and positrons (or \(\mu ^+\) and \(\mu ^-\)) but also corresponding ratios, for different centrality classes.

Our exploratory calculations have been done using impact parameter EPA. The discussed here electromagnetic effects were found at relatively small transverse momenta where more refined approach, including impact parameter-momentum correlations, may be necessary. Here we have discussed the differences of the approach only for the production cross section.

On the experimental side a good measurement of electrons and positrons at low transverse momenta (\(p_T<\) 0.1 GeV) is necessary to see an effect. In principle, the measurement of the \(\ell ^+ / \ell ^-\) ratio as a function of lepton rapidity and transverse momentum would be useful in this context. According to our knowledge, there are definite plans only for high energies (ALICE-3 project) where, however, the EM effect should be very small (high collision energy). At CERN SPS energies the effect is rather large but at very small transverse momenta. RHIC would probably be a good place to observe the effect of the discussed here EM interactions but this would require a modification of the present apparatus.

The discussed here effects could be interesting in future at the AFTER@LHC experiment [59, 60], where \(\sqrt{s_{NN}} \sim 100\) GeV. It may be also interesting to consider in future the problem in a quantal/field-theoretical approach, but this is not an easy task.