Experimental constraints on the properties of $P_c$ states

Abstract

Using new experimental data on photoproduction and $\Lambda _b^0$ decays, we derive constraints on the properties of the LHCb $P_c$ states. We conclude that $P_c(4312)$, $P_c(4380)$ and $P_c(4440)$ can be described as $\Sigma _c\bar{D}$, $\Sigma _c^*\bar{D}$ and $\Sigma _c\bar{D}^*$ molecules, but that $P_c(4457)$ does not fit into the same picture. Based on the apparent absence of additional partner states, and the striking disparity between $\Lambda _c^+\bar{D}^0$ and $\Lambda _c^+\bar{D}^{*0}$ decays, we conclude that $P_c(4440)$ has $3/2^-$ quantum numbers. Using heavy-quark symmetry we predict large experimental signals for $P_c$ states in $\eta _c p K^-$, $\Lambda _c^+\bar{D}^{*0}K^-$, and $\Sigma _c^{(*)}\bar{D}K^-$. We also argue that current experimental data on photoproduction is almost at the level of sensitivity required to observe $P_c$ states.

1 Introduction

The LHCb $P_c$ states have so far been observed only in the $J/\psi \, p$ spectrum of $\Lambda _b\rightarrow J/\psi \, p \,K^-$ decays [1,2,3], but experimental data from other processes can also usefully constrain their properties. In this paper we explore the consequences of some recent experimental observations whose implications for the phenomenology of the $P_c$ states have not been recognised in the literature. In particular, we consider: tighter constraints on photoproduction and $J/\psi \, p$ decays from the $J/\psi$-007 experiment, measurements of $\Lambda _b^0$ decays to $\Lambda _c^+\bar{D}^{0}K^-$, $\Lambda _c^+\bar{D}^{*0}K^-$ and $\eta _c p K^-$ (including limits on $P_c$ fit fractions), and the apparent absence of $P_c$ partners with higher mass.

In the molecular scenario, we find that these new experimental results imply constraints on the quantum numbers of $P_c$ states, and give striking predictions for prominent production channels that can be tested in experiment. Our observations follow directly from experiment, with minimal theoretical assumptions. At most, we rely only on symmetry principles which are well-justified theoretically and empirically: heavy-quark symmetry, and the dominance of colour-favoured processes in weak transitions.

We begin with an overview of molecular scenarios for the $P_c$ states (Sect. 2), and then review the recent experimental data which forms the basis of our analysis (Sect. 3). We then consider the resulting phenomenology associated with various decay modes, namely $J/\psi \, p$ (Sect. 4), $\eta _cp$ (Sect. 5), $\Lambda _c^+\bar{D}^0$ (Sect. 6), $\Lambda _c\bar{D}^{(*)}\pi$ (Sect. 7), $\Lambda _c^+\bar{D}^{*0}$ (Sect. 8) and $\Sigma _c^{(*)}\bar{D}$ (Sect. 9). We finally consider the implications of the apparent absence of heavier partners to the $P_c$ states (Sect. 10), and summarise our main results (Sect. 11).

Table 1 Quantum numbers and dominant degrees of freedom in the various scenarios

2 Scenarios

In the discovery paper [1], an amplitude analysis of $\Lambda _b\rightarrow J/\psi \, p \,K^-$ identified two states decaying to $J/\psi \, p$: the broad $P_c(4380)$ and narrower $P_c(4450)$. A model-independent analysis [2] confirmed the importance of including these contributions in adequately describing the data. A subsequent analysis, with an order of magnitude more data [3], discovered an additional new state $P_c(4312)$, and resolved the initial $P_c(4450)$ into two distinct, narrow peaks, $P_c(4440)$ and $P_c(4457)$.

The original $P_c(4380)$ did not feature in the newer analysis, which was sensitive only the narrow features in the spectrum. Because its discovery relied on an amplitude model which has been superseded, the existence or otherwise of $P_c(4380)$ remains to be determined experimentally, as explained in the note in the appendix of Ref. [3]. In our discussion we will refer to the “$P_c(4380)$”, although we will not insist that its measured properties are consistent with those extracted from the original analysis, which is regarded as obsolete.

Because of their proximity to thresholds, the $P_c$ structures are widely interpreted as molecular states whose wavefunctions are dominated by S-wave combinations of $\Sigma _c^{(*)}\bar{D}^{(*)}$ constituents [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. So $P_c(4312)$ is a $1/2^-$ $\Sigma _c\bar{D}$ state, while $P_c(4380)$ is $3/2^-$ $\Sigma _c^*\bar{D}$ state, albeit with significantly smaller width that the state observed in the original LHCb analysis. The $P_c(4440)$ and $P_c(4457)$ are both $\Sigma _c\bar{D}^*$ states, and can be assigned to either $1/2^-$ and $3/2^-$, or $3/2^-$ and $1/2^-$, respectively. We summarise these assignments in the first two rows of Table 1, where the Scenarios “A” and “B” correspond to those of Ref. [22].

The implicit assumption in most models is that the states are bound with respect to the nearest $\Sigma _c^{(*)}\bar{D}^{(*)}$ threshold, but experimentally, this has only been established for $P_c(4440)$. In Fig. 1 we show the binding energies of $P_c(4312)$, $P_c(4440)$ and $P_c(4457)$ with respect to their nearest thresholds. While $P_c(4440)$ is unambiguously bound with respect to $\Sigma _c^+\bar{D}^{*0}$, the masses of the other states are consistent, within uncertainties, with the thresholds.

The case of $P_c(4457)$ is particularly noteworthy. Its mass is consistent not only with the the $\Sigma _c^+\bar{D}^{*0}$ threshold but also, more strikingly, with $\Lambda _c(2595)\bar{D}$ threshold: the difference in the central values is just 0.2 MeV. This naturally suggests that for $P_c(4457)$, the $\Sigma _c\bar{D}^*$ bound state scenario is not the only possibility. In a forthcoming paper we explore a number of viable alternatives [31]. Given its proximity to threshold, the most prosaic option is that it is a threshold cusp arising from $\Sigma _c\bar{D}^*\rightarrow J/\psi \, p$ or $\Lambda _c(2595)\bar{D}\rightarrow J/\psi \, p$, or some combination of the two. Indeed the cusp scenario is favoured in the analysis of Ref. [32]. Alternatively, the peak could arise as a triangle singularity in $\Lambda _c(2595)\bar{D}$ or, as in our previous paper [24], as a genuine resonance, but with $1/2^+$ quantum numbers and $\Lambda _c(2595)\bar{D}$ degrees of freedom. We find that all of these scenarios give a very good fit to the $\Lambda _b\rightarrow J/\psi \, p \,K^-$ data [31].

Fig. 1

The binding energies of $P_c(4312)$, $P_c(4440)$ and $P_c(4457)$ with respect to their nearest thresholds. The $P_c(4380)$ is not shown, due to the large uncertainty in its mass (which overlaps considerably with the $\Sigma _c^*\bar{D}$ threshold)

It turns out to be very liberating to abandon the hypothesis that $P_c(4457)$ is a bound $\Sigma _c\bar{D}^*$ state, and not only because the alternative scenarios give a good fit to data. As we argue below, there are some phenomenological problems with the usual modelling, all of which can be traced to the assumption that $P_c(4457)$ is a bound $\Sigma _c\bar{D}^*$ state. By abandoning this assumption we avoid these problems.

Our alternative Scenario “C”, also shown in the Table 1, differs from the other two in no longer assuming that $P_c(4457)$ is a $\Sigma _c\bar{D}^*$ bound state. The assignments of the other states are consistent with Scenario B; the rationale for preferring $3/2^-$ quantum numbers for $P_c(4440)$ is explained below. Note that our Scenario C actually incorporates several possibilities, corresponding to different explanations for $P_c(4457)$.

Of course other scenarios are also discussed in the literature. In particular, we highlight Refs. [33, 34] in which non-resonant interpretations of $P_c(4312)$ have been discussed.

Table 2 Experimental data on the three-body branching fractions ${\mathcal {B}}$, and $P_c$ fit fractions ${\mathcal {R}}$, in $\Lambda _b^0$ decays. The sources of experimental data are described in the text. All upper limits are at 95% confidence level. As shown, in the case of $\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^0K^-$, the limits on fit fractions depend on the assumed quantum numbers ($1/2^-$ or $3/2^-$) of the $P_c$ states

3 Experimental data

In Table 2 we show the experimental data which forms the basis of much of our discussion. For each of four possible $\Lambda _b$ decays (indicated in the top row), we show the three-body branching fraction (${\mathcal {B}}$) and, where data are available, a measure (${\mathcal {R}}$) of the contribution of $P_c$ states in the fit, defined below. The data in the last three columns are quite new, and their significance has not yet been appreciated in literature.

The three-body branching fractions ${\mathcal {B}}$ for $\Lambda _b^0 \rightarrow J/\psi \, pK^-$ and $\Lambda _b^0 \rightarrow \eta _c pK^-$ are from LHCb [35,36,37], while those of $\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^0K^-$ and $\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^{*0}K^-$ are from Stahl [38], combining the measured ratios

$$\begin{aligned} \frac{{\mathcal {B}}(\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^0K^-)}{{\mathcal {B}}(\Lambda _b^0 \rightarrow \Lambda _c^+D_s^-)}&=(14.04\pm 0.58\pm 0.33\pm 0.45)\%, \end{aligned}$$

(1)

$$\begin{aligned} \frac{{\mathcal {B}}(\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^{*0}K^-)}{\mathcal B(\Lambda _b^0 \rightarrow \Lambda _c^+D_s^-)}&=(43.5\pm 1.4^{+1.2}_{-0.8}\pm 1.4)\%, \end{aligned}$$

(2)

from LHCb data, with the Particle Data Group (PDG) value for the denominators [37]

$$\begin{aligned} {\mathcal {B}}(\Lambda _b^0 \rightarrow \Lambda _c^+D_s^-)=(1.1\pm 0.1)\%. \end{aligned}$$

(3)

Fig. 2

Tree level contributions to three-body $\Lambda _b^0$ decays. Diagram (a) is colour-enhanced, whereas diagrams (b) and (c) are colour-suppressed

The quantity ${\mathcal {R}}$ is a measure of the contribution of the $P_c$ states in the fit, although the experimental procedures in how this number is computed differ. For $\Lambda _b^0 \rightarrow J/\psi \, pK^-$ and $\Lambda _b^0 \rightarrow \eta _c pK^-$, the numbers are from Refs. [3, 36], where they are described as “relative contributions”, and are identified in terms of branching fractions as

$$\begin{aligned} {\mathcal {R}}(J/\psi \, p) = \frac{ {{\mathcal {B}}}(\Lambda _b^0 \rightarrow P_c^+ K^-) \, {{\mathcal {B}}}(P_c^+ \rightarrow J/\psi \,p) }{ {{\mathcal {B}}}(\Lambda _b^0 \rightarrow J/\psi \, p\, K^-) }, \end{aligned}$$

(4)

and

$$\begin{aligned} {{\mathcal {R}} (\eta _c p)} = \frac{ {{\mathcal {B}}}(\Lambda _b^0 \rightarrow P_c^+ K^-) \, {{\mathcal {B}}}(P_c^+ \rightarrow \eta _c p) }{ {\mathcal B}(\Lambda _b^0 \rightarrow \eta _c p K^-) }. \end{aligned}$$

(5)

The numbers for $\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^0K^-$, from the amplitude analysis of Piucci [39], are “fit fractions”, defined in the usual way: the ratio, for a single resonance versus the full amplitude, of the phase space integrals of the square of the matrix element. (In the original $P_c$ discovery paper [1], the contributions of $P_c(4380)$ and $P_c(4450)$ were also quantified in terms of fit fractions.) We adopt the usual interpretation of the fit fraction, which is widespread in the experimental literature and the PDG [37], in terms of branching fractions, namely

$$\begin{aligned} {{\mathcal {R}} (\Lambda _c^+\bar{D}^0)} = \frac{ {{\mathcal {B}}}(\Lambda _b^0 \rightarrow P_c^+ K^-) \, {{\mathcal {B}}}(P_c^+ \rightarrow \Lambda _c^+\bar{D}^0) }{ {\mathcal B}(\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^0K^-) }. \end{aligned}$$

(6)

Note that the limits on the fit fractions depend on the assumed quantum numbers ($1/2^-$ or $3/2^-$) of the $P_c$ states, as shown in the table.

The difference between the “relative contributions” of Refs. [3, 36] and the “fit fractions” of Refs. [1, 39] relates to the treatment of interference terms, and is discussed in Ref. [3]. There is however no difference in the way the numbers are interpreted in terms of branching fractions, as shown in Eqs. (4), (5) and (6). Hence we will use the generic term “fit fraction”, and the same symbol ${{\mathcal {R}}}$, for both quantities.

We remark, however, that for both the “relative contributions” and “fit fractions”, the standard interpretation of these experimental numbers in terms of branching fractions has an implicit assumption, which is not necessarily justified. The factorisation of the numerator into a product of branching fractions is legitimate if the $P_c$ signal is due to a resonance, but not, for example, if it arises from a kinematical singularity or threshold cusp, in which case it is not possible (conceptually or mathematically) to separate the production ($\Lambda _b^0 \rightarrow P_c^+ K^-$) and decay (such as $P_c^+\rightarrow J/\psi \, p$). We discussed this point previously in relation to the X(2900) states [40], for which several competing interpretations are possible [41].

Much of our analysis below involves manipulations of measured ${\mathcal {R}}$ values, and in particular it relies on the standard factorisation of the branching fractions in the numerators. In our preferred Scenario C, we can only assume this factorisation for $P_c(4312/4380/4440)$, which we are treating as $\Sigma _c^{(*)}\bar{D}^{(*)}$ resonances. We cannot assume factorisation for $P_c(4457)$ because it is not justified for some of the scenarios applicable to this state (such as threshold cusp and triangle singularity); hence in much of the discussion below we will not consider $P_c(4457)$.

In computing the fit fractions ${{\mathcal {R}} (\Lambda _c^+\bar{D}^0)}$, the masses and widths of $P_c$ states, as determined in previous experiments, are taken as inputs [39]. For this reason we only quote the results for $P_c(4312/4440/4457)$, rather than those of the precursor states $P_c(4380/4450)$, whose mass and width measurements are considered to be obsolete [3].

There is a caveat on the limits on $\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^0K^-$ fit fractions that appear in the table. These were obtained by testing separately for the presence of a single state in the data – either $P_c(4312)$, $P_c(4440)$ or $P_c(4457)$ – rather than all three simultaneously. (The latter approach was found to be numerically unfeasible.)

While this suggests a degree of caution is warranted in interpreting the figures, it is reassuring to consider the results obtained for the precursor states $P_c(4380)$ and $P_c(4450)$, where both types of analyses were performed. The model in which both states were included simultaneously gives comparable, but somewhat tighter, upper limits on the branching fractions, compared to the model in which the presence of each state was tested separately. If the same applies in the case of $P_c(4312/4440/4457)$, the upper limits quoted in the table would be conservative.

The discussion so far has concentrated on $P_c$ states in 3-body $\Lambda _b$ decays. Another possibility, much discussed in the literature, is to search for the states in photoproduction [42,43,44,45,46,47]. Currently there is no evidence for $P_c$ states in $\gamma p\rightarrow P_c\rightarrow J/\psi \, p$, but the measured upper limits, which have recently become tighter, have interesting implications.

In particular, recall that the absence of the states in $\gamma p\rightarrow P_c\rightarrow J/\psi \, p$ implies upper limits, via vector meson dominance, on the $P_c\rightarrow J/\psi \, p$ branching fractions. After the initial discovery of the original LHCb states $P_c(4450)$ and $P_c(4380)$, analysis of photoproduction data available at the time implied an upper limit on the $J/\psi \, p$ branching fractions at the percent level [42]. More recently, the GlueX experiment [45] obtained similar upper limits from their new data, using a variant of the JPAC model for the amplitude [46]. The GlueX results assume $3/2^-$ quantum numbers for all the states, however choosing a different assignment is not expected to change the results drastically. The results are

$$\begin{aligned} {\mathcal {B}} (P_c^+\rightarrow J/\psi \, p)<(2.3\%\div 4.6\%), \end{aligned}$$

(7)

depending on which of $P_c(4312/4440/4457)$ is being considered.

These stringent upper limits have recently become even tighter: preliminary results from another Jefferson Lab experiment, $J/\psi$-007, indicate that the $J/\psi \, p$ upper limits are smaller than the GlueX limits by a factor of approximately 10 [47].

We may summarise the situation, rather roughly, as

$$\begin{aligned} {{\mathcal {B}}}(P_c^+\rightarrow J/\psi \, p)<(\text {a few})\times 10^{-3}. \end{aligned}$$

(8)

This is adequate for present purposes, as our arguments below only require estimates of the scales of the branching fractions, rather than their precise values. (We are also limited in not having an estimate of the systematic uncertainty associated with the assumed $3/2^-$ quantum numbers in the JPAC/GlueX analysis.)

4 $J/\psi \, p$ decays

We now come to the main thrust of the paper, exploring the implications of the experimental data discussed in the previous section. We begin with $J/\psi \, p$ decays, and note that the stringent upper limit (8) is in conflict with the vast majority of models, in some cases by orders of magnitude [4, 5, 9, 48,49,50,51,52,53, 53,54,55,56,57,58]. Our own estimate [24], for $P_c(4440)$, is one of very few that is consistent with (8). Similarly, Dong et al. [59] obtain a $P_c(4312)$ branching fraction which is near to the upper limit (8). Eides et al. [60] computed $J/\psi \, p$ branching fractions in both the molecular and hadrocharmonium pictures, noting a very different pattern in decays; their results for the molecular scenario, but not the hadrocharmonium scenario, are consistent with (8).

Superficially, the tight upper limit on $J/\psi \, p$ decays may appear surprising, considering that the $P_c$ states were of course discovered as prominent peaks in the $J/\psi \, p$ spectrum. This illustrates the point that in quantifying the prominence of a structure in the 2-body spectrum of a 3-body decay, the most relevant quantity is not the 2-body decay branching fraction itself, but the fit fraction ${\mathcal {R}}$. Recalling Eq. (4), the $P_c$ fit fractions are a measure of the fraction of all $J/\psi \, pK^-$ events that are produced via $\Lambda _b^0 \rightarrow P_c^+ K^-,P_c^+ \rightarrow J/\psi \,p$. Obviously, the fit fractions therefore depend not only on the properties of the $P_c$ states themselves (the production and decay branching fractions in the numerator), but also on the sum total of all other production mechanisms resulting in the $J/\psi \, pK^-$ final state (the denominator). It turns out that tree-level contributions to $J/\psi \, p\,K^-$ are suppressed, resulting in enhanced $P_c$ fit fractions.

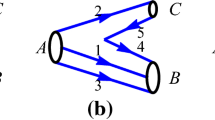
The suppression is explained in Fig. 2. There are three possible flavour topologies at the weak vertex (top panel), and for each, there is a corresponding three-body tree-level diagram that produces a kaon (bottom panel). The weak vertex in Fig. 2a is colour-enhanced, whereas those of Fig. 2b, c are colour-suppressed [24]. On this basis we expect, very roughly,

$$\begin{aligned}&{{\mathcal {B}}}(\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^{(*)0}K^-)>>{\mathcal B(\Lambda _b^0 \rightarrow c{\bar{c}}\, p\, K^-)} \nonumber \\&\quad \approx {\mathcal B(\Lambda _b^0 \rightarrow \Sigma _c^{(*)}\,\bar{D}^{(*)}\,K^-)}, \end{aligned}$$

(9)

which is consistent with the numbers in Table 2.

We conclude that the $P_c$ structures in $\Lambda _b^0 \rightarrow J/\psi \, p\, K^-$ are prominent (namely, have large fit fractions) in part because of the suppression of tree-level $\Lambda _b^0 \rightarrow J/\psi \, p\, K^-$ decays. Intriguingly, the situation is similar for several other exotic states observed in 3-body weak decays. For example, $\chi _{c1}(3872)$ [formerly X(3872)] has comparatively small branching fraction to $J/\psi \pi ^+\pi ^-$ and $J/\psi \omega$ [37], but was discovered and extensively studied in $B\rightarrow J/\psi \pi ^+\pi ^- K$ and $B\rightarrow J/\psi \omega K$, transitions for which the tree-level diagrams are also colour-suppressed. (Note that $\chi _{c1}(3872)$ has much larger branching fraction to $D^0\bar{D}^{*0}$, for example, but the tree-level diagram $D^0\bar{D}^{*0}K$ is colour-enhanced, and much larger.) In Ref. [40] we noted a similar mechanism enhancing the X(2900) signal in $B^+\rightarrow D^+X,X\rightarrow D^-K^+$ [61, 62].

We return now to the tighter upper limit (8) on $J/\psi \, p$ decays, and note that it has striking implications for $P_c$ production in $\Lambda _b^0$ decays. Upper limits on ${\mathcal B}(P_c^+ \rightarrow J/\psi \,p)$ imply lower limits on ${\mathcal B}(\Lambda _b^0 \rightarrow P_c^+\,K^-)$ [63]. Following our previous paper [24], in Fig. 3 we plot ${{\mathcal {B}}}(\Lambda _b^0 \rightarrow P_c^+\,K^-)$ as a function of ${{\mathcal {B}}}(P_c^+ \rightarrow J/\psi \,p)$, using Eq. (4), and the experimental values (Table 2) for ${{\mathcal {B}}}(\Lambda _b^0 \rightarrow J/\psi \, p\, K^-)$ and ${{\mathcal {R}}}(J/\psi \, p)$. We have also included $P_c(4380)$ in the plot, using the measured value [1]

$$\begin{aligned} {\mathcal {R}}(J/\psi \, p)&=(8.4 \pm 0.7 \pm 4.2)\%, \end{aligned}$$

(10)

although as noted below, this part of the plot should be interpreted with some caution. Note that in the plot we are showing the central values only; we do not include error bars, because the discussion below concerns the overall scale of the branching fractions, not their precise values.

Fig. 3

The branching fractions ${\mathcal {B}} (\Lambda _b^0\rightarrow P_c^+ K^-)$ as a function of ${\mathcal {B}} (P_c^+\rightarrow J/\psi \, p)$, obtained as described in the text

Combining Fig. 3 with Eq. (8) we conclude that ${\mathcal {B}} (\Lambda _b^0\rightarrow P_c^+ K^-)$ is at least ${{\mathcal {O}}}(10^{-3})$ for $P_c(4312/4440/4457)$, and ${\mathcal O}(10^{-2})$ for $P_c(4380)$. (These are larger by a factor of 10 than our previous estimates [24], because the limit on the $J/\psi \, p$ branching fraction is now smaller by a factor of 10.) Strikingly, these numbers are comparable to the largest measured two-body branching fraction for $\Lambda _b^0$ decays [37]

$$\begin{aligned} {{\mathcal {B}}}(\Lambda _b^0\rightarrow \Lambda _c^+D_s^-)=(1.1\pm 0.1)\%. \end{aligned}$$

(11)

The comparison is quite awkward because naively one would expect the production of multiquark states (whether molecular or compact) to be suppressed compared to that of conventional hadrons, and indeed that is what is observed in other sectors. The closest analogy is with $\chi _{c1}(3872)$, for which the measured branching fraction [37],

$$\begin{aligned} {{\mathcal {B}}}(B^+\rightarrow \chi _{c1}(3872)K^+)=(2.1\pm 0.7)\times 10^{-4}, \end{aligned}$$

(12)

is around a factor of fifty smaller than the corresponding branching fractions for conventional hadrons $B^+\rightarrow D_s^{(*)}\bar{D}^{(*)}$. Indeed, if anything, we would expect an even stronger relative suppression for the $P_c$ states because, unlike in the case of $\chi _{c1}(3872)$, their dominant wavefunction components cannot be produced in colour-favoured processes [24].

With this comparison in mind, the production branching fractions for $P_c(4380)$ seem implausibly large, but as noted previously, the numbers in this case should be treated with caution: we have used a measured fit fraction which, along with other properties of this state, are now considered to be obsolete [3].

But even the less dramatic numbers for $P_c(4312/4440/4457)$ present a challenge for models, and of course, the challenge becomes more acute as the limits on branching fractions ${\mathcal B}(P_c^+\rightarrow J/\psi \, p)$ become tighter. This suggests that ${\mathcal B}(P_c^+\rightarrow J/\psi \, p)$ cannot be much less than the current upper bound (8), otherwise ${\mathcal {B}} (\Lambda _b^0\rightarrow P_c^+ K^-)$ will become implausibly large. Indirectly, it suggests that the sensitivity required to observe $P_c$ states in photoproduction is not much more than that of the $J/\psi$ -007 experiment.

Note that the production branching fractions implied by the above analysis are orders of magnitude larger than those predicted by the effective Lagrangian approach of Ref. [64].

5 $\eta _c p$ decays

For $1/2^-$ states the S-wave decays to $J/\psi \, p$ and $\eta _c p$ are related by heavy-quark symmetry [19, 65]. In our Scenario C there is a single $1/2^-$ state, the $P_c(4312)$ with $\Sigma _c\bar{D}$ constituents. Ignoring differences due to phase space, the relation among branching fractions is

$$\begin{aligned} \frac{{{\mathcal {B}}}[P_c(4312)\rightarrow \eta _c p]}{{{\mathcal {B}}}[P_c(4312)\rightarrow J/\psi \, p]}=3. \end{aligned}$$

(13)

We conclude, by comparison to Eq. (8), that

$$\begin{aligned} {{\mathcal {B}}}[P_c(4312)\rightarrow \eta _cp]<{{\mathcal {O}}} (1\%) \end{aligned}$$

(14)

Nevertheless, the experimental prospects in $\Lambda _b\rightarrow \eta _c p K^-$ decays are encouraging: as noted previously, the relevant quantity is not the branching fraction ${{\mathcal {B}}}(P_c\rightarrow J/\psi \, p)$, but the fit fraction ${{\mathcal {R}}}(\eta _cp)$. From Eqs. (4) and (5) we find

$$\begin{aligned} \frac{{\mathcal {R}} (\eta _c p)}{{\mathcal {R}}(J/\psi \, p)}=3~\frac{{\mathcal B}(\Lambda _b^0 \rightarrow J/\psi \, p\, K^-)}{{{\mathcal {B}}}(\Lambda _b^0 \rightarrow \eta _c p K^-)} \end{aligned}$$

(15)

and thus, using the numbers from Table 2, we predict a substantial fit fraction for $P_c(4312)$:

$$\begin{aligned} {{\mathcal {R}}}(\eta _c p)=(2.7^{+4.3}_{-2.0})\% \end{aligned}$$

(16)

This is large in comparison to the fit fractions for the discovery mode $\Lambda _b^0 \rightarrow J/\psi \, p\, K^-$, suggesting the experimental prospects are encouraging. Note that the prediction is consistent with the experimental upper limit in Table 2.

As for the other states, for $P_c(4457)$ we cannot make any prediction for $\eta _cp$ decays in our Scenario C, without further modelling. (As noted previously, there are several viable scenarios for this state.) However for $P_c(4380)$ or $P_c(4440)$ we anticipate, on general grounds, negligible $\eta _cp$ signals, as they both have $3/2^-$ quantum numbers and thus do not couple to $\eta _c p$ in S-wave.

This is quite different from Scenarios A and B, in which one of $P_c(4440)$ or $P_c(4457)$ is a $\Sigma _c\bar{D}^*$ bound state with $1/2^-$ quantum numbers, and thus couples to $\eta _c p$ in S-wave. Drawing on the results of Ref. [65], we find

$$\begin{aligned} \frac{{\mathcal {R}} (\eta _c p)}{\mathcal R(J/\psi \, p)}=\frac{3}{25}~\frac{{{\mathcal {B}}}(\Lambda _b^0 \rightarrow J/\psi \, p\, K^-)}{{{\mathcal {B}}}(\Lambda _b^0 \rightarrow \eta _c p K^-)}. \end{aligned}$$

(17)

This implies, in comparison to Eq. (8), that if $P_c(4440)$ or $P_c(4457)$ is a $1/2^-$ state,

$$\begin{aligned} {{\mathcal {B}}}[P_c(4440/4457)\rightarrow \eta _cp]<{{\mathcal {O}}} (10^{-3}). \end{aligned}$$

(18)

In terms of fit fractions, in Scenario A we predict

$$\begin{aligned} {{\mathcal {R}}}(\eta _c p)=\left( 0.40^{+0.31}_{-0.29} \right) \% \end{aligned}$$

(19)

for $P_c(4440)$ and negligible $\eta _cp$ for $P_c(4457)$, whereas for Scenario B we predict

$$\begin{aligned} {{\mathcal {R}}}(\eta _c p)=\left( 0.19 \pm 0.16\right) \% \end{aligned}$$

(20)

for $P_c(4457)$, and negligible $\eta _cp$ for $P_c(4440)$. The ${{\mathcal {R}}}(\eta _cp)$ fit fractions in these scenarios are comparable to the measured ${{\mathcal {R}}}(J/\psi \, p)$ fit fractions in Table 2, suggesting such measurements may be within reach in future analyses. Confronting these predictions with data can discriminate among Scenarios A, B and C.

6 $\Lambda _c^+\bar{D}^0$ decays

We now turn to $\Lambda _c^+\bar{D}^0$ decays, which in many models are expected to be prominent channels. As we will see, this is not borne out by experimental data.

For a given $P_c$ state, combining Eqs. (4) and (6) yields a relation between the $\Lambda _c^+\bar{D}^0$ and $J/\psi \, p$ branching fractions

$$\begin{aligned} \frac{{{\mathcal {B}}}(P_c^+\rightarrow \Lambda _c^+\bar{D}^0)}{{{\mathcal {B}}}(P_c^+ \rightarrow J/\psi \,p) }=\frac{{{\mathcal {R}}}(\Lambda _c^+\bar{D}^0)}{{\mathcal R}(J/\psi \, p)}\frac{{{\mathcal {B}}(\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^0K^-)}}{{\mathcal B(\Lambda _b^0 \rightarrow J/\psi \, p\, K^-)} }. \nonumber \\ \end{aligned}$$

(21)

Taking the experimental data from Table 2 we obtain

$$\begin{aligned} \frac{{{\mathcal {B}}}(P_c^+\rightarrow \Lambda _c^+\bar{D}^0)}{{\mathcal B}(P_c^+ \rightarrow J/\psi \,p) }<(1.9\div 7.1), \end{aligned}$$

(22)

depending on which of the states $P_c(4312/4440/4457)$ is considered, and its assumed quantum numbers. In combination with the photoproduction upper limit (8), we arrive at the surprising result

$$\begin{aligned} {\mathcal B}(P_c^+\rightarrow \Lambda _c^+\bar{D}^0)\lesssim \mathcal O(1\%). \end{aligned}$$

(23)

We will show later that this limit argues in favour of Scenario C.

Table 3 Relative matrix elements for S-wave transitions $\Sigma _c^{(*)}\bar{D}^{(*)}\rightarrow \Lambda _c\bar{D}^{(*)}$, according to heavy-quark symmetry. The values are extracted from Ref. [30], but apply not only to contact terms in effective field theory, but also to the central potentials due to one-pion exchange. The lower part of the table identifies the various scenarios

7 $\Lambda _c\bar{D}^{(*)}\pi$ decays

In previous sections we observed that the $P_c$ branching fractions to $J/\psi \, p$, $\eta _c p$ and $\Lambda _c^+\bar{D}^0$ are tiny. This implies that their measured decay widths,

$$\begin{aligned} \Gamma [P_c(4312)]&=9.8\pm 2.7^{+3.7}_{-4.5}~\text {MeV}, \end{aligned}$$

(24)

$$\begin{aligned} \Gamma [P_c(4440)]&=20.6\pm 4.9^{+8.7}_{-10.1}~\text {MeV}, \end{aligned}$$

(25)

$$\begin{aligned} \Gamma [P_c(4457)]&=6.4\pm 2.0^{+5.7}_{-1.9}~\text {MeV}, \end{aligned}$$

(26)

must be dominated by other modes. One possibility is three-body decays which, in the molecular scenario, would arise via the decay of a constituent hadron. Given that $\bar{D}$ is stable and $\bar{D}^*$ has negligible decay width, molecular three-body decays are presumably dominated by $\Sigma _c\rightarrow \Lambda _c\pi$ or $\Sigma _c^*\rightarrow \Lambda _c\pi$ [66]. Following Refs. [24, 65, 67], we assume that the three-body width is determined by the width of the $\Sigma _c^{(*)}$ constituent, resulting in the following predicted partial widths

$$\begin{aligned} \Gamma [P_c(4312)\rightarrow \Lambda _c^+\bar{D}\pi ]&=1.9~\text {MeV} \end{aligned}$$

(27)

$$\begin{aligned} \Gamma [P_c(4380)\rightarrow \Lambda _c^+\bar{D}\pi ]&=15~\text {MeV} \end{aligned}$$

(28)

$$\begin{aligned} \Gamma [P_c(4440/4457)\rightarrow \Lambda _c^+\bar{D}^{*}\pi ]&=1.9~\text {MeV} \end{aligned}$$

(29)

Evidently these three-body decays cannot account entirely for the measured $P_c$ decay widths. Given the tiny $J/\psi \, p$ branching fractions, we also disregard more esoteric possibilities like $\chi _{c0}p$ and $J/\psi N\pi$.

8 $\Lambda _c^+\bar{D}^{*0}$ decays

We have established that the partial widths of $P_c$ states to $J/\psi \, p$, $\eta _c p$ and $\Lambda _c^+\bar{D}^0$ are tiny, and that three-body modes, while not negligible, cannot account for the measured decay widths. The rest of the decay width must be accounted for by other modes. We assume that decays to exclusively light-flavoured hadrons are small; this is because of the OZI rule, and the apparent absence of prominent light-flavoured decays in other hidden-charm states.

In the case of $P_c(4312)$ we conclude, by a process of elimination, that the dominant decay must be $\Lambda _c^+\bar{D}^{*0}$, as this is the only two-body mode with hidden charm which is kinematically accessible. Ignoring the small contributions from $J/\psi \, p$, $\eta _c p$ and $\Lambda _c^+\bar{D}^0$, we estimate the $\Lambda _c^+\bar{D}^{*0}$ partial width by taking the difference of Eqs. (24) and (27),

$$\begin{aligned} \Gamma [P_c^+(4312)\rightarrow \Lambda _c^+\bar{D}^{*0}]=2.7\div 12.5~\text {MeV}, \end{aligned}$$

(30)

where we have combined the statistical and systematic uncertainties in (24) in quadrature. We have not accounted for the uncertainties in Eq. (27), because of the difficulty in quantifying the systematic uncertainty on the underlying assumption, namely that the three-body width is equal to the width of the free constituents. Most of our arguments below relate to the scale of the experimental numbers, not their precise values, so we do not expect the conclusions to be compromised by the unquantified uncertainties.

One may question the validity of predicting prominent $\Lambda _c^+\bar{D}^{*0}$ modes on the basis of a process of elimination. However we also note that our conclusion is supported by model calculations which confirm the prominence of $\Lambda _c^+\bar{D}^{*0}$ decays in molecular models [9, 13, 25, 51, 52, 59].

From our estimate (30), the corresponding branching fraction

$$\begin{aligned} {{\mathcal {B}}}[P_c^+(4312)\rightarrow \Lambda _c^+\bar{D}^{*0}]=59\%\div 87\%, \end{aligned}$$

(31)

is enormous in comparison to the closely related $\Lambda _c^+\bar{D}^0$ mode, Eq. (23). The challenge for models is to explain the striking disparity between these two modes which would naively be expected to be comparable. We will see that this issue argues in favour of our Scenario C.

Heavy quark symmetry implies relations among all couplings of the type $\Sigma _c^{(*)}\bar{D}^{(*)}\rightarrow \Lambda _c^+\bar{D}^{0(*)}$. In Table 3 we show the relative matrix elements for S-wave transitions obtained assuming heavy-quark symmetry, taken from the potentials in Ref. [30]. Note that the relative matrix elements apply not only to effective field theory models, where the S-wave potentials correspond to contact terms that are fit to data, but also to models where the transition is due to the central potential from one-pion exchange (since such models satisfy heavy-quark symmetry).

The first thing to notice is that for $P_c(4312)$, modelled as a $1/2^-$ $\Sigma _c\bar{D}$ state, the striking disparity in the magnitudes of $\Lambda _c\bar{D}$ and $\Lambda _c\bar{D}^*$ has a natural explanation, and confirms a selection rule predicted by Voloshin [65]. Although conservation of angular momentum allows for decays to both $\Lambda _c\bar{D}$ (in S-wave) and $\Lambda _c\bar{D}^*$ (S-wave and D-wave), the $\Lambda _c\bar{D}$ decay is forbidden by heavy-quark symmetry. In this sense the experimental data are nicely consistent with the molecular model for $P_c(4312)$. (The suppression of the $\Lambda _c\bar{D}$ mode is also a feature of the chiral constituent quark model [59], and the chromomagnetic pentaquark model [68], but not the model of Ref. [25].)

The tight upper limit (23) on $\Lambda _c\bar{D}$ decays also has a natural explanation for $3/2^-$ states, both $P_c(4380)$ ($\Sigma _c^*\bar{D}$) and $P_c(4440/4457)$ ($\Sigma _c\bar{D}^*$). In these cases the $\Lambda _c\bar{D}$ decay would be D-wave, hence suppressed compared to the S-wave decay $P_c(4312)\rightarrow \Lambda _c\bar{D}^*$.

On the other hand, for a $1/2^-$ $\Sigma _c\bar{D}^*$ state, the tight upper limit on $\Lambda _c^+\bar{D}^0$ is a problem. The previous argument relies on the assumption (which is very natural) that D-wave decays are suppressed compared to S-wave decays. In that case, the $\Lambda _c\bar{D}$ and $\Lambda _c\bar{D}^*$ partial widths for the various $P_c$ states are dominated by the S-wave matrix elements, so we can estimate the relative strengths using the numbers in Table 3. We notice in particular that for $1/2^-$, the $\Sigma _c\bar{D}^*\rightarrow \Lambda _c^+\bar{D}^0$ matrix element is identical to $\Sigma _c\bar{D}\rightarrow \Lambda _c^+\bar{D}^{*0}$, whose scale is set by Eq. (30). This is a problem for Scenarios A and B, because it implies that if either of $P_c(4440)$ or $P_c(4457)$ were a $1/2^-$ $\Sigma _c\bar{D}^*$ state, then its $\Lambda _c^+\bar{D}^0$ partial width would be $2.7\div 12.5$ MeV, indeed even larger because of the enhanced phase space compared to the $P_c(4312)$ decay. This is wildly inconsistent with the upper limit of Eq.  (23).

To avoid this problem, we have to abandon the assumption that there is a $1/2^-$ $\Sigma _c\bar{D}^*$ bound state, which leads us to Scenario C. Since for $P_c(4457)$ there are several viable alternatives, we assume that only $P_c(4440)$ is $\Sigma _c\bar{D}^*$ bound state, and that its quantum numbers are $3/2^-$. We will argue later that there are other reasons to favour this over the alternative Scenarios A and B.

In summary, there is an apparent tension between the dominance of the $P_c(4312)\rightarrow \Lambda _c^+\bar{D}^{*0}$ decays, and the tight experimental upper limits on $P_c\rightarrow \Lambda _c^+\bar{D}^0$. This is a problem for Scenarios A and B, but not for Scenario C, where the $\Lambda _c^+\bar{D}^0$ decays are small either due to their D-wave nature (for the $3/2^-$ states) or because of heavy quark symmetry (for $P_c(4312)$).

From now on we concentrate on Scenario C. We may estimate the $\Lambda _c\bar{D}^*$ partial widths of $P_c(4380)$ and $P_c(4440)$ using Eq. (30) and the numbers in Table 3:

$$\begin{aligned} \Gamma [P_c^+(4380)\rightarrow \Lambda _c^+\bar{D}^{*0}]&=2.7\div 12.5~\text {MeV}, \end{aligned}$$

(32)

$$\begin{aligned} \Gamma [P_c^+(4440)\rightarrow \Lambda _c^+\bar{D}^{*0}]&=0.9\div 4.2~\text {MeV}. \end{aligned}$$

(33)

Here we have ignored the effect of the mass differences between $P_c(4312)$, $P_c(4380)$ and $P_c(4440)$. (Phase space would enhance the decays of the heavier states, but this is to some extent mitigated by a corresponding form factor suppression in the matrix element.)

For $P_c(4380)$ we assume the decay width is saturated by $\Lambda _c^+\bar{D}^{*0}$ and, from Eq. (28), $\Lambda _c\bar{D}\pi$. This is because of the tight upper limit on $J/\psi \, p$, and the absence of other two-body S-wave decays. (We are assuming that the D-wave decay to $\Sigma _c\bar{D}$ is small.) This suggests a total width

$$\begin{aligned} \Gamma [P_c(4380)]=17.7\div 27.5~\text {MeV}, \end{aligned}$$

(34)

considerably smaller than the measured width [1] which, however, is considered to be obsolete [3]. Other approaches also find a narrower $P_c(4380)$ [15, 30]. Assuming our estimated total width, the $\Lambda _c\bar{D}^*$ branching fraction is

$$\begin{aligned} {{\mathcal {B}}}[P_c(4380)\rightarrow \Lambda _c\bar{D}^*]=15\%\div 45\%. \end{aligned}$$

(35)

If neglected decays (notably the $\Sigma _c\bar{D}$ D-wave) are significant, this will be an overestimate.

For $P_c(4440)$, the $\Lambda _c\bar{D}^*$ branching fraction is

$$\begin{aligned} {{\mathcal {B}}}[P_c(4440)\rightarrow \Lambda _c\bar{D}^*]=3\%\div 45\%, \end{aligned}$$

(36)

where we have used the measured total width, Eq. (31), with statistical and systematic uncertainties combined in quadrature.

Given the predicted large $\Lambda _c^+\bar{D}^{*0}$ branching fractions for $P_c(4312)$, $P_c(4380)$ and $P_c(4440)$, searching for these states in $\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^{*0}K^-$ is warranted. We note that this decay has already been observed at LHCb [38], although an amplitude analysis has not been carried out.

To understand the experimental prospects in these channels, we consider now the fit fraction

$$\begin{aligned} {{\mathcal {R}} (\Lambda _c^+\bar{D}^{*0})} = \frac{ {{\mathcal {B}}}(\Lambda _b^0 \rightarrow P_c^+ K^-) \, {{\mathcal {B}}}(P_c^+ \rightarrow \Lambda _c^+\bar{D}^{*0}) }{ {\mathcal B}(\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^{*0}K^-) }. \end{aligned}$$

(37)

We may eliminate the unknown production branching fraction ${{\mathcal {B}}}(\Lambda _b^0 \rightarrow P_c^+ K^-)$ by taking a ratio with Eq. (4), to give

$$\begin{aligned} \frac{{\mathcal {R}} (\Lambda _c^+\bar{D}^{*0})}{{\mathcal {R}} (J/\psi \, p)} = \frac{{{\mathcal {B}}}(\Lambda _b^0 \rightarrow J/\psi \, p\,K^-) }{{\mathcal B}(\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^{*0}K^-) } \frac{{{\mathcal {B}}}(P_c^+ \rightarrow \Lambda _c^+\bar{D}^{*0})}{{{\mathcal {B}}}(P_c^+ \rightarrow J/\psi \, p)}. \end{aligned}$$

(38)

Using the experimental numbers in Table 2, and our estimates of ${{\mathcal {B}}}(P_c^+ \rightarrow \Lambda _c^+\bar{D}^{*0})$, we have a relation between the fit fractions ${\mathcal {R}} (\Lambda _c^+\bar{D}^{*0})$ and the branching fraction ${{\mathcal {B}}}(P_c^+ \rightarrow J/\psi \, p)$, which we plot in Fig. 4. Because we are interested in the scale of the numbers rather than their precise values, for illustration we plot the central values only. For $P_c(4380)$, we have used the obsolete value of the fit fraction, Eq. (10).

Fig. 4

The fit fractions ${{\mathcal {R}}}(\Lambda _c^+\bar{D}^{*0})$ as a function of ${{\mathcal {B}}}[P_c(4312)\rightarrow J/\psi \, p]$, obtained as described in the text

The message of this plot, when combined with the upper limit (8), is that the fit fractions ${{\mathcal {R}} (\Lambda _c^+\bar{D}^{*0})}$ are enormous. Indeed for $P_c(4380)$ the predicted fit fractions are implausibly large. We attribute this to the use of the obsolete value (10) when constructing the plot. (We encountered a similar problem when interpreting Fig. 3.)

For $P_c(4312)$ and $P_c(4440)$, the fits fractions of order ${{\mathcal {O}}}(10\%)$ or larger are still plausible, but are strikingly large when compared to the ${{\mathcal {O}}}(1\%)$ fit fractions in the observed $J/\psi \, p$ mode (Table 2). It suggests of course that there are strong prospects for the experimental observation of these states in $\Lambda _b^0 \rightarrow \Lambda _c^+\bar{D}^{*0}K^-$.

A corollary of this plot is that the branching fraction ${\mathcal B}[P_c(4312)\rightarrow J/\psi \, p]$ cannot be much less than the current bound in Eq. (8), otherwise the fit fractions ${\mathcal R}(\Lambda _c^+\bar{D}^{*0})$ become implausibly (or impossibly) large. We arrived at the same conclusion when interpreting Fig. 3. As discussed there, this also implies that observation of $P_c$ states in photoproduction requires not much more sensitivity than that of the $J/\psi$ -007 experiment.

9 $\Sigma _c^{(*)}\bar{D}$ decays

In molecular models, couplings of the type $\Sigma _c^{(*)}\bar{D}^{(*)}\rightarrow \Sigma _c^{(*)}\bar{D}^{(*)}$ are responsible for binding. The same couplings will also lead to decays into $\Sigma _c^{(*)}\bar{D}$ final states, where phase space is available. The $P_c(4312)$ is too light, but $P_c(4380)$ could decay into $\Sigma _c\bar{D}$ (in D-wave), and $P_c(4440)$ could decay into both $\Sigma _c\bar{D}$ (in D-wave) and $\Sigma _c^*\bar{D}$ (in S-wave and D-wave), where we assume the $3/2^-$ quantum numbers of Scenario C. We further assume that S-wave decays dominate over D-waves, in which case the most prominent decay will be $P_c(4440)\rightarrow \Sigma _c^*\bar{D}$. Note that having accounted for $\Lambda _c^+\bar{D}^{*0}$ and $\Lambda _c\bar{D}^*\pi$ decays, in Eqs. (29) and (33), respectively, the measured width (25) still allows for a considerable $\Sigma _c^*\bar{D}$ mode. We also note that various models find substantial $\Sigma _c^*\bar{D}$ decays, for example Refs [25, 51].

The experimental prospects for observing $P_c(4380)$ or $P_c(4440)$ in $\Lambda _b^0 \rightarrow \Sigma _c^{(*)}\bar{D}K^-$ depend on the fit fraction

$$\begin{aligned} {{\mathcal {R}} (\Sigma _c^{(*)}\bar{D})} = \frac{ {{\mathcal {B}}}(\Lambda _b^0 \rightarrow P_c^+ K^-) \, {{\mathcal {B}}}(P_c^+ \rightarrow \Sigma _c^{(*)}\bar{D}) }{ {{\mathcal {B}}}(\Lambda _b^0 \rightarrow \Sigma _c^{(*)}\bar{D}K^-) }. \end{aligned}$$

(39)

Taking a ratio with Eq. (4), we get a relation between ${\mathcal {R}} (\Sigma _c^{(*)}\bar{D})$ and ${\mathcal {R}} (J/\psi \, p)$,

$$\begin{aligned} \frac{{\mathcal {R}} (\Sigma _c^{(*)}\bar{D})}{{\mathcal {R}} (J/\psi \, p)} = \frac{{\mathcal B}(\Lambda _b^0 \rightarrow J/\psi \, p\,K^-) }{{{\mathcal {B}}}(\Lambda _b^0 \rightarrow \Sigma _c^{(*)}\bar{D}K^-) } \frac{{{\mathcal {B}}}(P_c^+ \rightarrow \Sigma _c^{(*)}\bar{D})}{{{\mathcal {B}}}(P_c^+ \rightarrow J/\psi \, p)}. \end{aligned}$$

(40)

As far as we know, ${{\mathcal {B}}}(\Lambda _b^0 \rightarrow \Sigma _c^{(*)}\bar{D}K^-)$ has not been measured, but since the tree-level contributions to this mode are colour suppressed (Fig. 2), we expect it to be comparable to ${{\mathcal {B}}}(\Lambda _b^0 \rightarrow J/\psi \, p\,K^-)$, as noted in Eq. (9). In this case, we expect the first ratio on the right-hand side of Eq. (40) to be a number of order 1. Conversely, because of the stringent upper limit (8) on $P_c^+\rightarrow J/\psi \, p$, we expect the second ratio on the right-hand side to be large, at least for $P_c(4440)\rightarrow \Sigma _c^*\bar{D}$, where the S-wave is expected to be prominent. We conclude that for $P_c(4440)^+$, the fit fraction ${\mathcal {R}} (\Sigma _c^*\bar{D})$ ought to be large in comparison to the measured fit fraction ${\mathcal {R}} (J/\psi \, p)$, implying strong experimental prospects. Depending on the magnitude of the D-wave decays, by a similar argument we may also expect considerable (albeit smaller) fit fractions ${\mathcal {R}} (\Sigma _c\bar{D})$ for $P_c(4380)$ and $P_c(4440)$.

This is another example of the general phenomenon discussed in Sect. 4. Where tree-level three-body decays are suppressed, two-body fit fractions can be large.

Finally, we remark that, assuming the $P_c$ states are isospin 1/2, the different charge modes $\Lambda _b^0 \rightarrow \Sigma _c^{(*)+}\bar{D}^0 K^-$ and $\Lambda _b^0 \rightarrow \Sigma _c^{(*)++} D^- K^-$ have relative rates 1 : 2. Deviations from this would be an indication of isospin mixing [66].

10 Partner states

Given the existence of states near the thresholds for $\Sigma _c\bar{D}$, $\Sigma _c^*\bar{D}$ and $\Sigma _c\bar{D}^*$, the apparent absence of states near $\Sigma _c^*\bar{D}^*$ threshold is conspicuous. In this section we show that this is a problem for Scenarios A and B, but not for Scenario C.

Interactions among $\Sigma _c^{(*)}\bar{D}^{(*)}$ channels are constrained by heavy-quark symmetry. This applies both to models based on meson exchange, and also effective field theory approaches where the long-range contribution to the potential is due to pion-exchange, and the short-range part is modelled via contact terms that are fit to data. The pattern of binding in such models can be understood qualitatively with reference to the simplest approach, where the potentials are due to S-wave contact terms only (no meson exchange). The elastic potentials, from Ref. [69], are given in Table 4.

Table 4 S-wave elastic potentials for $\Sigma _c^{(*)}\bar{D}^{(*)}$ molecules constrained by heavy quark symmetry

Clearly, binding in $\Sigma _c\bar{D}$ and $\Sigma _c^*\bar{D}$ requires $C_a<0$. The potentials in these channels are identical, so apart from small differences due to their masses, and coupled-channel effects, binding in one channel implies binding in the other. Thus a model that accounts for $P_c(4312)$ inevitably implies a partner state $P_c(4380)$.

To get binding in both of the $\Sigma _c\bar{D}^*$ channels, and thus account for both $P_c(4440)$ and $P_c(4457)$, requires $C_a$ to be large enough (in magnitude) compared to $C_b$. Scenarios A and B are then distinguished by having $C_b>0$ and $C_b<0$, respectively.

With $C_a$ large (in magnitude) compared to $C_b$, on the basis of the potentials in Table 4 it seems likely that all three of the $\Sigma _c^*\bar{D}^*$ states ($1/2^-$, $3/2^-$ and $5/2^-$) will also bind, and that expectation is confirmed by calculation [22]. This immediately raises the question of why there is apparently no evidence for such states in the experimental data. The absence of the $5/2^-$ state may be understood from its lack of S-wave coupling to $J/\psi \, p$; it decays in D-wave, which may be expected to be suppressed. However the missing $1/2^-$ and $3/2^-$ states are more problematic.

It is possible that Scenarios A and B may be rescued with the idea that the extra $\Sigma _c^*\bar{D}^*$ states do exist, but are just not seen in $\Lambda _b\rightarrow J/\psi \, p \,K^-$ because of suppressed production or decays. But in the model we propose [31] the situation is precisely the opposite. From heavy quark symmetry, the production and decay of the $3/2^-$ $\Sigma _c^*\bar{D}^*$ state, in particular, would be enhanced compared to other observed states, so if there is binding in this channel, it ought to be visible as a prominent peak in $\Lambda _b\rightarrow J/\psi \, p \,K^-$. Similarly, the $1/2^-$ $\Sigma _c^*\bar{D}^*$ state would be expected to decay prominently $\Lambda _c\bar{D}$; there is no obvious indication of structure in the $\Lambda _b^0\rightarrow \Lambda _c^+\bar{D}^0 K^-$ spectrum [39], but more detailed analysis with more statistics could be revealing.

The inevitability of binding in all three $\Sigma _c^*\bar{D}^*$ channels ($1/2^-$, $3/2^-$ and $5/2^-$) is a problem that is intrinsic to Scenarios A and B. As noted, to get binding in both $\Sigma _c\bar{D}^*$ channels ($1/2^-$ and $3/2^-$) implies that $C_a$ must be large in magnitude compared to $C_b$, which in turn renders all of the $\Sigma _c^*\bar{D}^*$ channels sufficiently attractive to cause binding.

It all plays out very differently if only one of the two $\Sigma _c\bar{D}^*$ were required to bind. In this case it is no longer necessary to have $C_a$ large (in magnitude) in comparison to $C_b$, with the consequence that binding is not automatic in all channels. Indeed, this scenario was already considered after the initial LHCb paper, when the experimental data suggested one $\Sigma _c\bar{D}^*$ state, not two [69].

If only one of the $\Sigma _c\bar{D}^*$ channels binds, it is natural to associate this with $P_c(4440)$, since this is unambiguously below $\Sigma _c\bar{D}^*$ threshold. As discussed previously, there are several viable alternative scenarios for $P_c(4457)$, because its mass is consistent with $\Sigma _c\bar{D}^*$ and $\Lambda _c(2595)\bar{D}$ thresholds. The next question is whether $P_c(4440)$ has $1/2^-$ or $3/2^-$ quantum numbers. In Sect. 6 we argued in favour of $3/2^-$ quantum numbers (what we called Scenario C), noting that the tight upper limits on $\Lambda _c^+\bar{D}^0$ decays are not consistent with a $1/2^-$ $\Sigma _c\bar{D}^*$ state. We will now show that the pattern of binding also argues in favour of the $3/2^-$ assignment.

With reference to Table 4, to achieve $\Sigma _c\bar{D}^*$ binding in $3/2^-$, but not $1/2^-$, implies $C_b<0$. This in turn suggests that out of the $\Sigma _c^*\bar{D}^*$ states, there is binding in $5/2^-$, but not $1/2^-$ or $3/2^-$, and indeed this expectation is borne out in explicit calculation [69]. This spectrum of states is nicely consistent with the absence of $\Sigma _c^*\bar{D}^*$ states in the data. The $1/2^-$ and $3/2^-$ states simply don’t exist, and the $5/2^-$ state is not visible because its decay is suppressed. (In our model [31] we find that not only the decay, but also the production, of the $5/2^-$ state is suppressed.)

The alternative scenario does not work so well. If instead we assume $\Sigma _c\bar{D}^*$ binding in $1/2^-$ (but not $3/2^-$), we need $C_b>0$, which implies $\Sigma _c^*\bar{D}^*$ binding in $1/2^-$ and $3/2^-$ (but not $5/2^-$). In this scenario one needs an explanation for why the $1/2^-$ and $3/2^-$ $\Sigma _c^*\bar{D}^*$ states are not visible in $\Lambda _b\rightarrow J/\psi \, p \,K^-$. (Note that some authors do argue in favour of the $C_b>0$ pattern, for other reasons [70, 71].)

Another reason to prefer binding $\Sigma _c\bar{D}^*$ in $3/2^-$ is that it is also consistent with expectations from one-pion exchange. In Table 5 we show the central potentials due to pion-exchange obtained from the quark model [24, 69], where C(r) behaves as a Yukawa function (with positive sign) for large r (i.e. it is repulsive at large r). It follows that the attractive channels are those in which C(r) comes with a negative coefficient, namely $\Sigma _c\bar{D}^*$ in $3/2^-$ and $\Sigma _c^*\bar{D}^*$ in $5/2^-$; this is consistent with the pattern of binding in our Scenario C.

Of course the arguments about attraction and repulsion in one-pion exchange are admittedly simplistic, particularly because they ignore the tensor potential, which is known to be important for binding. Nevertheless, explicit calculation including the tensor terms confirms that the channels that bind most easily (requiring the smallest form factor cutoff) are those identified above [18, 24, 69]. The pattern also applies to models where the potential is due to exchange of not only pions, but also other light mesons [17, 27].

Table 5 S-wave elastic potentials for $\Sigma _c^{(*)}\bar{D}^{(*)}$ molecules from one-pion exchange in the quark model, where C(r) is the potential defined in Ref. [24]

(Notice that the pion exchange potentials in Table 5 follow the same pattern as the “$C_b$” contact terms in Table 4, under the replacement $C_b\rightarrow -3 C(r)$. This is ultimately because both contributions are proportional to an operator of the form ${\mathbf {S}}_1\cdot {\mathbf {S}}_2$, where $\mathbf{S}_1$ and ${\mathbf {S}}_2$ are vectors acting on the spin degrees of freedom of the $\Sigma _c^{(*)}$ and $\bar{D}^{(*)}$, respectively.)

11 Conclusions

We have shown that, with minimal theoretical assumptions, current experimental data on $\Lambda _b$ decays and photoproduction imply constraints on the quantum numbers of $P_c$ states, and lead to predictions for their decay branching fractions, and fit fractions in $\Lambda _b^0$ decays to $\eta _c p K^-$, $\Lambda _c^+\bar{D}^{*0}K^-$, and $\Sigma _c^{(*)}\bar{D}K^-$.

Unlike the usual Scenarios A and B, where $P_c(4440)$ and $P_c(4457)$ are both $\Sigma _c\bar{D}^*$ bound states, in our Scenario C only $P_c(4440)$ is a bound state, and its quantum numbers are $3/2^-$. Because the $P_c(4457)$ mass coincides with both $\Sigma _c\bar{D}^*$ and $\Lambda _c(2595)\bar{D}$ thresholds, there are several viable alternatives for this state, which we explore in future work [31]. The cusp interpretation of $P_c(4457)$ is favoured by Ref. [32].

One of the advantages of Scenario C is that, unlike Scenarios A and B, it is consistent with the striking observation that the $P_c$ states hardly decay to $\Lambda _c^+\bar{D}^0$, but apparently decay prominently to $\Lambda _c^+\bar{D}^{*0}$. The suppression of $\Lambda _c^+\bar{D}^0$ is natural for $P_c(4312)$, where it is forbidden by heavy-quark symmetry, and for $P_c(4380)$ and $P_c(4440)$ which, as $3/2^-$ states, decay to $\Lambda _c^+\bar{D}^0$ in D-wave. The problem with Scenarios A and B is that each has a $1/2^-$ $\Sigma _c\bar{D}^*$ state which, from heavy quark symmetry, should decay prominently to $\Lambda _c^+\bar{D}^0$, in conflict with experimental data.

Another issue with Scenarios A and B is that they imply the existence of $\Sigma _c^*\bar{D}^*$ partner states, with quantum numbers $1/2^-$, $3/2^-$ and $5/2^-$, which are not apparent in $\Lambda _b\rightarrow J/\psi \, p\, K^-$ data. This is an inevitable consequence of fixing the potential parameters in order to generate two $\Sigma _c\bar{D}^*$ bound states, with both $1/2^-$ and $3/2^-$ quantum numbers. Our Scenario C naturally avoids this issue, as we only require a single $\Sigma _c\bar{D}^*$ state with $3/2^-$ quantum numbers. In this case the potentials are such that the $1/2^-$ and $3/2^-$ $\Sigma _c^*\bar{D}^*$ partners do not bind, and while the $5/2^-$ $\Sigma _c^*\bar{D}^*$ partner does bind, its absence in experiment can be understood as a consequence of D-wave suppression both in decay and, as discussed in our next paper [31], production.

A further advantage of Scenario C is that it reproduces the pattern of binding expected on the basis of one-pion exchange.

We have given many predictions for the branching fractions and $\Lambda _b^0$ fit fractions of $P_c(4312)$, $P_c(4380)$ and $P_c(4440)$ in various modes. The most striking prediction is for strong experimental signals for all the states in $\Lambda _b^0\rightarrow \Lambda _c^+\,\bar{D}^{*0}\,K^-$. This is a particularly sharp prediction when juxtaposed against the absence of signals in the closely related decay $\Lambda _b^0\rightarrow \Lambda _c^+\,\bar{D}^{0}\,K^-$. The decay $\Lambda _b^0\rightarrow \Lambda _c^+\,\bar{D}^{*0}\,K^-$ has been observed at LHCb [38], and we suggest an amplitude analysis to test for the existence of $P_c$ states in the $\Lambda _c^+\,\bar{D}^{*0}$ spectrum.

In $\Lambda _b^0\rightarrow \eta _c\,p\,K^-$, we predict a substantial $P_c(4312)$ fit fraction, which can be tested in future experimental analyses. (Our prediction is consistent with the current upper bound.) In our Scenario C, we do not expect prominent signals for the other $P_c$ states in $\Lambda _b\rightarrow \eta _c\,p\,K^-$. We showed that, by contrast, Scenarios A and B could be distinguished by the relative fit fractions of $P_c(4440)$ and $P_c(4457)$.

We also predict strong experiment signals for $P_c(4440)$ in $\Lambda _b^0 \rightarrow \Sigma _c^*\bar{D}K^-$, and smaller signals for both $P_c(4380)$ and $P_c(4440)$ in $\Lambda _b^0 \rightarrow \Sigma _c\bar{D}K^-$.

We also pointed out that the branching fractions ${\mathcal B}(P_c^+\rightarrow J/\psi \, p)$ cannot be much less than the current upper bound (8), otherwise the production branching fractions ${\mathcal {B}} (\Lambda _b^0\rightarrow P_c^+ K^-)$ and fit fractions ${{\mathcal {R}}}(\Lambda _c^+\bar{D}^{*0})$ would be implausibly large. (See Figs. 3 and 4.) An interesting consequence is that existing experimental measurements are almost at the level of sensitivity required to observe $P_c$ states in photoproduction.

We want to emphasise that many of the constraints and predictions we have derived are very general in nature, and so if it turns out they are not satisfied by future experimental data, it could be an indication not of the failure of our particular realisation of the molecular model, but of the molecular approach all together. As an example, consider again the observation (Fig. 3) that if the upper limit on ${{\mathcal {B}}}(P_c^+\rightarrow J/\psi \, p)$ is much less than Eq. (8), it would imply implausibly large production branching fractions ${\mathcal {B}}(\Lambda _b^0\rightarrow P_c^+K^-)$. In this case some new mechanism would need to be invoked to explain how, contrary to intuition, molecular states are produced with comparable branching fraction to conventional hadrons. Alternatively, since the observation is a direct consequence of the measured fit fractions, one could question whether or not it is appropriate, in the fit fraction, to factorise the production and decay branching fractions ${\mathcal {B}}(\Lambda _b^0\rightarrow P_c^+K^-)$ and ${{\mathcal {B}}}(P_c^+\rightarrow J/\psi \, p)$ in the numerator. The factorisation is legitimate in the case that $P_c$ is a resonance, but not if the $P_c$ signal is an effect which is uniquely associated with a particular production mechanism, such as a cusp or triangle singularity. Indeed we gave examples, in the case of the X(2900) states, where the factorisation is clearly not appropriate [40]. Many of our manipulations in this paper rely on this factorisation, and so our predictions should be interpreted with this in mind.