Abstract
The mass shifts for two-fermion bound and scattering P-wave states subject to the long-range interactions due to QED in the non-relativistic regime are derived. Introducing a short range force coupling the spinless fermions to one unit of angular momentum in the framework of pionless EFT, we first calculate both perturbatively and non-perturbatively the Coulomb corrections to fermion–fermion scattering in the continuum and infinite volume context. Motivated by the research on particle–antiparticle bound states, we extend the results to fermions of identical mass and opposite charge. Second, we transpose the system onto a cubic box with periodic boundary conditions and we calculate the finite volume corrections to the energy of the lowest bound and unbound \(T_1^{-}\) eigenstates. In particular, power law corrections proportional to the fine structure constant and resembling the recent results for S-wave states are found. Higher order contributions in \(\alpha \) are neglected, since the gapped nature of the momentum operator in the finite-volume environnement allows for a perturbative treatment of the QED interactions.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Preamble
Effective field theories [1,2,3,4,5,6,7,8] nowadays play a fundamental role in the description of many-body systems in nuclear and subnuclear physics, employing the quantum fields which can be excited in a given regime of energy. Once the breakdown scale \(\varLambda \) of the EFT is set, the scattering amplitudes are usually expressed in power series of \(p/\varLambda \), where p represents the characteristic momentum of the processes under consideration. The Lagrangian density is typically written in terms of local operators of increasing dimensions obeying pertinent symmetry constraints.
Moreover, power counting rules establish a hierarchy among the interaction terms to include in the Lagrangian, thus permitting to filter out the contributions that become relevant only at higher energy scales [7].
In the case of systems of stable baryons at energies lower than the pion mass, the Lagrangian density contains only the nucleon fields and their Hermitian conjugates, often combined toghether with differential operators. The corresponding theory, the so-called pionless EFT [2, 9,10,11,12] counts a number of successes in the description of nucleon–nucleon scattering and structure properties of few-nucleon systems. Despite the original difficulties in the reproduction of S-wave scattering lengths, that were solved via the introduction of the Power Divergence Subtraction (PDS) as a regularization scheme [10, 13, 14], the theory has permitted so far to reproduce the \({}^1S_0\) np phase shift [15, 16], structure properties of the triton as a dn S-wave compound [12, 17, 18] and the scattering length [19, 20] and the phase shift [21,22,23] of the elastic dn scattering process.
In the first applications of QED in pionless EFT, the electromagnetic interactions were treated perturbatively, as in the case of the electromagnetic form factor [24] and electromagnetic polarizability [25] for the deuteron or the inelastic process of radiative neutron capture on protons [26]. Afterwards, a non-perturbative treatment of electromagnetic (Coulomb) interactions on top of the same EFT was set up, in the context of proton-proton S-wave elastic [27] and inelastic [28, 29] scattering.
Inspired by the P-wave interactions presented in refs. [30,31,32], we generalize in the first part of the present paper the analysis in Ref. [27] to fermion-fermion low-energy elastic scattering ruled by the interplay between the Coulomb and the strong forces transforming as the \(\ell =1\) representation of the rotation group (cf. Ref. [33] for the empirical S- and P-wave phase shifts in the pp case). As in Ref. [27], we treat the Coulomb photon exchanges both in a perturbative and in a non-perturbative fashion. During the derivation of the T-matrix elements, we observe that at sufficiently low energy the repulsion effects from the Coulomb ladders become comparable to the ones of the strong forces, leading to the breakdown of the perturbative regime of non-relativistic QED. In the determination of the closed expressions for the scattering parameters in terms of the coupling constants, we take advantage of the separation of the Coulomb interaction from the strong forces, considered first in Refs. [34,35,36] and eventually generalized to strong couplings of arbitrary angular momentum \(\ell \) in Ref. [37]. The importance of particle-antiparticle systems led us to the applicaton of the formalism to fermion-antifermion scattering, where the attractive Coulomb force gives rise to bound states. This case provides a laboratory for the study of \(p{\bar{p}}\) bound [38] and unbound states [39], also referenced as protonium.
Of fundamental importance for the study of few- and many-particle systems with QED are Lattice Effective Field Theories and Lattice Quantum Chromodynamics (LQCD). The latter has matured to the point where basic properties of light mesons and baryons are being calculated at or close to the physical pion mass [40, 41]. In particular, in the case of the lowest-lying mesons, their properties are attaining a level of accuracy where it is necessary to embed the strong interactions within the full standard model [42,43,44,45,46,47]. Despite the open computational challenges represented by the inclusion of the full QED in LQCD simulations, in the last decade quenched QED [48] together with flavour-symmetry violating terms have been included in the Lagrangian, with the aim of reproducing some features of the observed hadron spectrum [49,50,51,52,53,54,55,56,57].
Conversely, the perspective to add QED interactions in LQCD simulations for systems with more than three nucleons appears still futuristic, due to the limitations in the computational resources. Nevertheless, the interplay between QCD and QED has been very recently explored also in the ground state energy of bound systems up to three nucleons like deuteron, \({^3}\hbox {H}\) and \({^3}\hbox {He}\) in Ref. [65]. Additionally, in two-body processes like \(\pi ^{\pm } \pi ^{\pm }\) [58, 59, 65], \(\overline{K}^0\overline{K}^0\) [65] and nucleon-meson scattering [65], the time is ripe for the introduction of electromagnetic interactions in the present LQCD calculations.
It is exactly in this context that, in the second part of the paper, we immerse our fermion–fermion EFT into a cubic box with periodic boundary conditions (PBC). The finite-volume environment has a number of consequences, the most glaring of them are the breaking of rotational symmetry [60,61,62,63] and the discretization of the spectrum of the operators representing physical observables [64, 66, 67]. Concerning the Hamiltonian, its spectrum consists of levels that in the infinite-volume limit become part of the continuum (scattering states) and in others that are continuously transformed into the bound states. For two- and three-body systems governed by strong interactions, the shifts of the bound energy levels with respect to the counterparts at infinite volume depend on the spatial extent of the cubic volume L through negative exponentials, often multiplied by nontrivial polynomials in L. Apart the pioneering work on two-bosons subject to hard-sphere potentials in Ref. [68], these effects for two-body systems have been extensively analyzed by Lüscher in Refs. [69, 70] ([71]), where the energy of the lowest unbound (bound) states has been expressed in terms of the scattering parameters and the box size.
In the last three decades, Lüscher formulas for the energy shifts have been extended in several directions including non-zero angular momenta [66, 72,73,74] moving frames [74,75,76,77,78,79,80], generalized boundary conditions [81,82,83,84,85,86] and particles with intrinsic spin [87, 88]. Moreover, considerable advances have been made in the derivation of analogous formulas for the energy corrections of bound states of three-body [67, 89, 90] and N-body systems [91]. See also the review [92].
However, the presence of the long-range interactions induced by QED leads to significant modifications in the form of the corrections associated to the finite volume energy levels. Irrespective on whether a state is bound or unbound, in fact, the energy shifts take the form of polynomials in the reciprocal of the box size [40] and the exponential damping factors disappear. Moreover, the gapped nature of the momentum of the particles in the box allows for a perturbative treatment of the QED contributions, even at low energies [40, 41, 48, 93, 94]. In this regime, composite particles receive corrections of the same kind both in their mass [40] and in the energies of the two-body states that they can form [94].
As shown in Ref. [94], the leading-order energy shift for the lowest S-wave bound state is proportional to the fine-structure constant and has the same sign of the counterpart in absence of QED, presented in Refs. [66, 72]. In the second part of this work, we demonstrate that the same relation holds for the lowest bound P-wave state, whose finite volume correction is negative as the one for the counterpart without electromagnetic interactions. Additionally, we prove that the QED energy-shifts for S- and P-wave eigenstates have the same magnitude if order \(1/L^3\) terms are neglected, a fact that remains valid in the absence of interactions of electromagnetic nature. At least for the \(\ell =0\) and 1 two-body bound eigenstates, in fact, the sign of the correction depends directly on the parity of the wavefunction associated to the energy state, whose tails are truncated at the boundaries of the cubic box, as observed in Ref. [66].
Although bound states between two hadrons of the same charge have not been observed in nature, at unphysical values of the quark masses in Lattice QCD these states do appear [125,126,127,128]. It is possible that such two-body bound states manifest themselves also when QED is included in the Lagrangian. Moreover, two-boson bound states originated by strong forces are expected to explain certain features of heavy quark compounds. In particular, the interpretation of observed lines Y(4626), Y(4630) and Y(4660) of the hadron sprectrum in terms of P-wave \([cs][{\bar{c}} {\bar{s}}]\) tetraquark states with \(1^{--}\) seems promising [95].
Pairwise interesting are recent studies on proton–ptoton collisions, which revealed the presence of intermediate P-wave \(\varDelta N\) states with spin 0 and 2 at 2.197(8) and 2.201(5) GeV respectively, see ref [96]. Although these states are not classified as dibaryons [97] because of their large decay width (\(\varGamma \gtrsim 100\) MeV) [96, 98], an attractive force appears to lower the expected energy of the \(\varDelta - N\) system by \(\approx 30\) MeV.
Additionally, loosely bound binary compounds of hadrons appearing in the vicinity of a P-wave strong decay threshold are not forbidden by the theory of hadronic molecules [99]. Possible candidates of such two-body systems are represented by the hidden charm pentaquark states \(P_c^+(4380)\) and \(P_c^+(4450)\), located slightly below the \({\bar{D}}\varSigma _c^*\) and \({\bar{D}}^*\varSigma _c\) energy thresholds at 4385.3 MeV and 4462.2 MeV, respectively. Although a wide variety of different studies on the two states have been conducted [100,101,102], a very recent one advances the molecular hypotesis [103] with orbital angular momentum equal to one in the framework of heavy quark spin symmetry (HQSS).
Concerning scattering states, the energy shift formula for the lowest P-wave state that we present in this paper has close similarities with the one in Ref. [94], despite an overall \(\xi /M \equiv 4\pi ^2/M L^2\) factor, owing to the fact that the energy of the lowest unbound state with analogous transformation properties under discrete rotations (\(T_1\) irrepFootnote 1 of the cubic group) is different from zero. Additionally, further scattering parameters appear in the expression for the \(\ell = 1\) finite volume energy correction, even as coefficients of the smallest powers of 1/L.
The present article is structured into two parts and its content can be summarized as follows. After this preamble, the theoretical framework that is the basis for both the infinite and the finite volume treatment is introduced, by starting from the Lagrangian with the strong P-wave interactions alone. Next, in the end of Sect. 2, the T-matrix for two-body fermion–fermion scattering to all orders in the strength parameter of the potential is computed. Subsequently, in Sect. 2.1, non-relativistic QED is presented in the same fashion of Refs. [104, 105] and the Lagrangian is reduced to the case of spinless fermions and electrostatic interactions. After displaying the amplitudes corresponding to tree-level and one-loop diagrams with one Coulomb photon exchange, the non-perturbative treatment of the Coulomb interaction is implemented. To this aim, we resort to the formalism of Ref. [27], that we recapitulate in the end of Sect. 2.1. As in the introductory section, the T-matrix matrix element accounting for both Coulomb and strong interactions is derived to all orders in \(\alpha \), thanks to the Dyson-like identities that hold among the free, the Coulomb and the full two-body Green’s functions. As in Ref. [27], Sect. 2.2 closes with the expressions of the scattering length and the effective range in terms of the physical constants of our EFT Lagrangian, that are obtained from the effective-range expansion. The first part of the analysis is concluded in Sect. 2.3 with the calculation of the same amplitude for the fermion–antifermion scattering case. The reader already experienced with the dimensional regularization integrals in Sects. 2.2 and 2.3 may skip the details of the derivation and focus directly on the results presented in Eqs. (89) and (126) respectively.
Then, the two fermion-system is transposed onto a cubic spatial volume of size L and the distortions induced by the new environment in the laws of electrodynamics [40, 106] and in the masses of possibly composite particles [40] are briefly summarized in Sect. 3. Next, the quantization conditions, that give access to the energy spectrum in finite volume though the expression of the T-matrix elements [94], are displayed and discussed (Sect. 3.1) in the perturbative regime of QED. Analogously, the reader already experienced with suchs derivations is encouraged to focus the attention directly on Eq. (175).
Next, the finite volume counterpart of the \(\ell =1\) effective range expansion is presented, together with the expressions of the new Lüscher functions, shown in the end of Sect. 3.2. Subsequently, the energy eigenvalues of the lowest bound and scattering states are presented along with the details of the whole derivation, which can be skipped by a reader already aquainted with the extraction of energy eigenvalues from the effective range expansion as in Ref. [94]. The pivotal results of the calculation are indeed given by the concluding formulas of Sects. 3.3.1 and 3.3.2, that is Eqs. (218)–(219) and Eqs. (231)–(232). In the section that follows some hints are given regarding the consequences of the addition of transverse photon interactions within our EFT for Coulomb and strong forces coupled to one unit of angular momentum.
The general conclusions of our work are drawn in Sect. 5, where the main results are qualitatively recapitulated. The appendices provide supplemental material to the reader interested in the derivation of the scattering amplitudes in Sects. 2.2 and 2.3 and/or in the three-dimensional Riemann sums arising from the approximations of the Lüscher functions in Sects. 3.1, 3.2 and 3.3.
2 Effective field theory for non-relativistic fermions
Our analysis of two-particle scattering and bound states in the infinite- and finite-volume context is based on pionless effective field theory [9, 10, 13, 14, 107,108,109,110]. The theory, developed more than two decades ago [9], describes the strong interactions between nucleons at energy scales smaller than the pion mass, \(M_{\pi }\) [7, 27, 107]. The action is non-relativistic and is constructed by including all the possible potential terms made of nucleon fields and their derivatives, fulfilling the symmetry requirements of the strong interactions at low energies (i.e. parity, time reversal and Galilean invariance) [111]. The importance of the various interaction terms decreases with their canonical dimension while approaching the zero energy limit. Besides, even the dominant contribution at low energies for local contact interactions between four-nucleon fields is of dimension six, thus making the theory non-renormalizable [27] in the classical sense.
Analogously to Ref. [94], we begin by extending pionless EFT to spinless fermions of mass M and charge e, and we assume that the theory is valid below an upper energy \(\varLambda _{E^*}\) in the center-of-mass frame (CoM). More specifically, if the fermions represent hadrons, the latter energy cutoff can be chosen to coincide with the pion mass. Second, we construct the interactions in terms of four-fermion operators, selecting the ones that transform explicilty as the \(2\ell +1\)-dimensional irreducible representation of \(\mathrm {SO(3)}\),
where \({\mathcal {P}}_{\ell }\) is a Legendre polynomial, \(\pm {\mathbf {p}}\) (\(\pm {\mathbf {q}}\)) are the three-momenta of two incoming (outcoming) particles in the CoM frame, such that \(|{\mathbf {p}}| = |{\mathbf {q}}|\), \(\hat{{\mathcal {V}}}^{(\ell )}\) is the potential in terms of second quantized operators and the \(c_{2j}^{(\ell )}\) are low-energy (LECs) constants, whose importance at low-energy scales diminishes for increasing values of j . In particular, for the three lowest angular momentum couplings (\(\ell \le 2\)), the interaction potentials take the form
and
As shown in sect. II of Ref. [94], the terms in Eq. (2) (Eqs. (3), (4)) proportional to even powers of the momentum (a gradient expansion in configuration space), can be encoded by a single interaction with energy-dependent coefficient \(C(E^*)\) (\(D(E^*)\) and \(F(E^*)\)) for S-waves (P- and D-waves), where \(E^*\) represents the CoM energy of the colliding particles, equal to \(2M + {\mathbf {p}}^2/M\). While the case of fermions coupled to zero angular momentum via a single contact interaction proportional to \(C(E^*)\) is the starting-point of the analysis in Ref. [94], the fundamental P-wave interaction in Eq. (3) with energy-dependent coefficient \(D(E^*)\) becomes the key tool of the present investigation. Although interactions of the same form have been already adopted in pionless EFT for nucleons (cf. Eq. (4) in Ref. [30]) and in EFT with dimeron fields (cf. Eq. (2) in Ref. [112]), the P-wave counterpart of Kong and Ravndal’s analysis on fermion–fermion scattering in Ref. [27] is not available in the literature.
Adopting the conventions of Ref. [30] for the coupling constants (cf. the Feynman rules in App. A), the Lagrangian density assumes the form
where \(\overleftrightarrow {\nabla } = \overleftarrow{\nabla } - \overrightarrow{\nabla }\) denotes the Galilean invariant derivative for fermions. Recalling the Feynman rules in App. A, two-body elastic scattering processes without QED are represented by chains of bubbles, analogous to the ones in Fig. 3 in Ref. [27]. In particular, the tree-level diagram, consisting of a single four-fermion vertex, leads to an amplitude equal to \(-\mathrm {i}D(E^*) {\mathbf {p}}\cdot {\mathbf {p}}'\) (cf. Ref. [32]) where \(\pm {\mathbf {p}}\) and \(\pm {\mathbf {p}}'\) are, respectively, the momenta of the incoming and outcoming particles in the CoM frame. As a consequence, the two-body \(\ell =1\) (pseudo)potential in momentum space takes the form
which coincides with the tree-level diagram multiplied by the imaginary unit.
Tree-level (upper line, left), 1-loop (upper line, right) and n-loops diagrams (lower line) representing fermion-fermion elastic scattering with the strong P-wave potential in Eq. (6)
Considering also the other possible diagrams in momentum space with amputated legs in Fig. 1, the expression for the full scattering amplitude due to strong interactions can be written as,
where \({\hat{G}}_0^{E} \equiv {\hat{G}}_0^{(+)}(E)\) is the two-body unperturbed retarded \((+)\) Green’s function operator,
with \({\hat{H}}_0\) the two-body free Hamiltonian in relative coordinates \({\hat{H}}_0 = \hat{{\mathbf {p}}}^2/M\), and M/2 is the reduced mass of a system of identical fermions. Inserting a complete set of plane wave eigenstates \(|{\mathbf {q}},-{\mathbf {q}}\rangle \equiv |{\mathbf {q}}\rangle \) in the numerator, the latter expression becomes
where \(E = {\mathbf {p}}^2/M\) is the energy eigenvalue at which the retarded \((+)\) and advanced \((-)\) Green’s functions are evaluated. In configuration space the latter take the form
that is diagrammatically depicted by two propagation lines. The explicit computation of the three lowest order contributions to the sum in Eq. (7) yields
and
where \(\partial _i \equiv \partial /\partial r_i\), \(\partial _i' \equiv \partial /\partial r_i'\) and \(\partial _i'' \equiv \partial /\partial r_i''\), while \({\mathbb {J}}_{0}\) is a symmetric matrix whose elements are given by
and Einstein’s index convention is henceforth understood. Extending the computation to higher orders, it is evident that the infinite superposition of chains of bubbles translates into a geometric series in the total scattering amplitude, as in the \(\ell =0\) case, and a formula analogous to Eq. (2) in Ref. [27] is obtained,
Furthermore, performing the Fourier transform of the potential in Eq. (6) into configuration space,
the full scattering amplitude can be recovered independently in position space by means of partial integrations and cancellations of surface integrals at infinity,
The matrix elements of \({\mathbb {J}}_{0}\) can be, now, evaluated by dimensional regularization. Applying the formula in Eq. (B18) of Ref. [113] for d-dimensional integration, Eq. (14) in arbitrary d-dimensions becomes
where \(\mu \) is the renormalization scale introduced by the minimal subtraction (MS) scheme. Like the S-wave counterpart, the integral proves to be finite in three dimensions and, within this limit is given by
where the energy E in the CoM frame has been eventually expressed as \({\mathbf {p}}^2/M\). For the sake of completeness, we derive the contribution to \(({\mathbb {J}}_{0})_{ij}\) from the power divergence subtraction (PDS) regularization scheme, in which the power counting of the EFT is manifest [10, 14]. To this aim, the eventual poles of the regularized integral for \(d\rightarrow 2\) should be taken into account. In this limit, it turns out from Eq. (18) that the Euler’s Gamma has a pole singularity of the kind \(2/(2-d)\). As a consequence, the original dimensional regularization result in Eq. (18) acquires a finite PDS contribution, transforming into
This can be compared with the one in Eq. (4) in Ref. [27] for the S-wave interactions. Since the \({\mathbb {J}}_0\) matrix is diagonal (Eq. (20)), few efforts are needed for the computation of the fermion–fermion scattering amplitude,
With reference to scattering theory [114], the \(T_{\mathrm {S}}\) matrix for P-wave elastic scattering with phase shift \(\delta _1\) can be written as
where \(\theta \) is the angle between the incoming and outcoming direction of particles in the CoM frame. Recalling the effective-range expansion (ERE) for \(\ell =1\) scattering [114],
an expression for the scattering parameters in terms of the momenta of the particles, the coupling constant and the mass M can be drawn. In particular, a formula for the scattering length analogous to Eq. (2.16) of Ref. [14] can be recovered,
Furthermore, the effective range parameter \(r_0\) vanishes, as in the zero angular momentum case. Plugging the PDS-regularized expression of \({\mathbb {J}}_{0}\) in Eq. (20) into Eq. (15) and exploiting the ERE again, finally, the renormalized form of the coupling constant \(D(E^*)\) is obtained,
Unlike in the \(\ell =0\) case, we note that the \(\mu \)-dependent version of \(D(E^*) = 12\pi a/M\) is quadratic in the momentum of the incoming fermions.
2.1 Coulomb corrections
We introduce the interactions of electromagnetic nature in the non Lorentz-covariant fashion of Refs. [104] and [105]. The formalism of non-relativistic quantum electrodynamics (NRQED), introduced in Ref. [104], is designed to reproduce the low-momentum behaviour of QED to any desired accuracy. Besides, only non-relativistic momenta are allowed in the loops and in the external legs of the diagrams. The contributions arising from relativistic momenta in the QED loops, in fact, are absorbed as renormalizations of the coupling constants of the local interactions in the non-relativistic counterpart of QED [104]. The Lagrangian is determined by the particle content and by the symmetries of the theory, such as gauge invariance, locality, hermiticity, parity conservation, time reversal symmetry and Galilean invariance. The particles are fermionic, characterized by mass M and unit charge e, and are represented by two-component non-relativistic Pauli spinor fields \(\varPsi \). In compliance to these prescriptions, the NRQED Lagrangian density in Ref. [104] assumes the form,
where \({\mathbf {D}} = \nabla + \mathrm {i}e{\mathbf {A}}\) is the covariant derivative, while \({\mathbf {E}} = -\nabla \phi -\partial _t {\mathbf {A}}\) and \({\mathbf {B}} = \nabla \times {\mathbf {A}}\) denote the electric and magnetic fields, respectively. The terms in the first row encode the leading ones of \({\mathcal {L}}^{\mathrm {NRQED}}\), containing the minimal coupling of the fermionic fields with the vector potential \({\mathbf {A}}\) and the scalar potential, \(\phi \). The interactions proportional to the constants \(c_1\)-\(c_4\) and \(d_1\) in Eq. (26) are next-to-leading-order terms, corresponding to corrections of order \(v^4/c^4\) and \(v^6/c^6\), respectively [105], whereas the ellipses represent contributions containing higher order covariant derivatives, \({\mathcal {O}}(v^8/c^8)\).
Since the Coulomb force dominates at very low energies and transverse photons couple proportionally to the fermion momenta, in the present treatment we choose to retain in the Lagrangian only the scalar field and its lowest order coupling to the fermionic fields as in Ref. [27]. Moreover, we reduce the latter to spinless fields \(\psi \), consistently with Sect. 2 and with Ref. [94]. As a consequence, the full Lagrangian density of the system becomes the superposition of the one in Eq. (5) with the one involving the electrostatic potential and its leading order coupling to the spinless fermions, namely
Alternatively, on top of the P-wave interaction in Eq. (6) the Coulomb force, that in momentum space is regulated by an IR cutoff \(\lambda \), reads
has been added. The introduction of the electrostatic potential generates the additional Feynman rules listed in App. A. Consequently, the T-matrix is enriched by new classes of diagrams (cf. Fig. 2), in which the Colulomb photon insertions either between the external legs and within the loops begin to appear. Unlike transverse photons, the scalar ones do not propagate between different bubbles.
From the Feynman rules, the amplitude for the tree-level diagram with one photon insertion in the left part of Fig. 2 gives,
After integrating over the free energy \(l_0\), the tree-level amplitude in Eq. (29) can be decomposed as follows
In particular, in the last rewriting the first integral on the r.h.s. turns out to be identical to the one in Eq. (9) of Ref. [27] except for the factor \({\mathbf {p}}\cdot {\mathbf {p}}' = {\mathbf {p}}^2 \cos \theta \), therefore it can be immediately integrated. Conversely, the last integral in Eq. (30) represents a new contribution, whose evaluation in dimensional regularization is carried out in App. B. Adding the two contributions together, the tree level amplitude with Coulomb photon insertion in Eq. (30) becomes
where the limit \(\lambda \rightarrow 0\) for the \({\mathcal {O}}(\lambda )\) terms is understood. From the last equation we infer that, due to the linear dependence in the momenta of the incoming particles \({\mathbf {p}}\) in the CoM frame, P-wave fermion-fermion scattering is suppressed with respect to the S-wave one in the low-\({\mathbf {p}}\) limit. However, both the \(\ell =0\) and \(\ell =1\) tree level amplitudes with one Coulomb photon insertion are divergent in the \(\lambda \rightarrow 0\) limit.
Nevertheless, due to the fact that the latter logarithmic contribution is imaginary, the infinite term does not contribute to the \({\mathcal {O}}(\alpha )\) corrections of the strong cross section, which is proportional to \(|C(E^*) + T_{\mathrm {SC}}^{\mathrm {tree}}|^2 \approx C(E^*)\) \(\cdot [C(E^*) + 2 \mathfrak {Re}T_{\mathrm {SC}}^{\mathrm {tree}}]\) up to first order in \(\alpha \). The corrected cross section to that order turns out to be IR finite and proportional to \(1-\pi \eta \), where \(\eta = \alpha M/2|{\mathbf {p}}|\) for particles with equal unit charge. As observed in Ref. [27], the inclusion of n Coulomb photon exchanges leads to corrections proportional to \(\eta ^n\) in the cross section. Therefore, the feasibility of a perturbative treatment for the Coulomb force is regulated by the smallness of the parameter \(\eta \), i.e. by a constraint on the momenta of the incoming particles, \(|{\mathbf {p}}| \gg \alpha M/2\). As a consequence, if the momenta of the incoming particles are too small, the Coulomb force is expected to have a strong influence on the cross-section of the elastic process and a non-perturbative treatment becomes necessary.
Furthermore, the Feynman rules for the one-loop diagram with one photon insertion on the right part of Fig. 2 yield
Similarly, the contour integration with respect to the free energies \(k_0\) and \(l_0\), followed by the momentum translation \({\mathbf {l}}\mapsto {\mathbf {q}}\equiv {\mathbf {l}}-{\mathbf {k}}\), leads to
The remaining momentum integrations are performed in dimensional regularization (cf. Sect. B) and give
where \(\epsilon \equiv d -3\) and \(\gamma _E \approx 0.5772\) denotes the Euler-Mascheroni constant. The amplitude in Eq. (34) displays a pole at \(d = 3\) as the one in Eq. (15) of Ref. [27], an ultraviolet divergence that can be reabsorbed with a redefinition of the strength parameter \(D(E^*)\) via the renormalization process. However, \(T_{\mathrm {SC}}^{\mathrm {1-loop}}\) is devoid of the logarithmic divergence in the zero-momentum limit, due to the multiplication by a factor \({\mathbf {p}}^2\). Consequently, in comparison with the zero angular momentum counterpart, the \(\ell =1\) one-loop scattering amplitude with one-photon insertion is suppressed in the limit of zero momentum \({\mathbf {p}}\) of the incoming particles in the CoM frame. Since \(T_{\mathrm {SC}}^{\mathrm {1-loop}}\) possesses also a pole in the \(d\rightarrow 2\) limit, the implementation of the PDS scheme results into an additional term proportional to the renormalization scale (or mass),
Differently from the \(\ell =0\) counterpart in Eq. (14) of Ref. [27], the logaritmic term in the CoM momentum of the colliding fermions does not give rise to a divergence in the zero momentum limit, due to the \({\mathbf {p}}^4\) prefactor. Nevertheless, the dressing of the one-bubble diagram with two or more Coulomb photon insertions results in the multiplication of \(T_{\mathrm {SC}}^{\mathrm {1-loop}}\) by one or more powers of \(\eta = \alpha M /2 |{\mathbf {p}}|^2\), so that, at order higher than four in \(\alpha \), the amplitude becomes singular in the limit \(|{\mathbf {p}}| \rightarrow 0\). It follows that the perturbative approach breaks down and the effects of Coulomb repulsion need to be treated to all orders in \(\alpha \).
Since our interest resides in the low-momentum sector of fermion-fermion elastic scattering, we incorporate the Coulomb ladders in the amplitude of the process to all orders in the fine structure constant. For scalar photons, this amounts to replacing the free-fermion propagators in the bubble diagrams of Fig. 1 with the Coulomb propagators in Fig. 3. To this aim, we follow the procedure outlined in Ref. [27] and introduce the Coulomb Green’s functions. The inclusion of the Coulomb potential (cf. Eq. (28)) in the Hamiltonian yields the Coulomb Green’s function operator,
an expression that, together with Eq. (8), admits a self-consistent rewriting à la Dyson [115],
that can be diagrammatically represented as in Fig. 3.
Moreover, the solutions of Schrödinger equation with a repulsive Coulomb potential, \(({\hat{H}}_0 + V_{\mathrm {C}}-E)|\varPsi _{{\mathbf {p}}}^{(\pm )}\rangle \), can be formally expressed in terms of the free ones as
see Eq. (18) in Ref. [27]. The above eigenstates share with the plane waves the generalized normalization property, i.e. \(\langle \psi _{{\mathbf {p}}}^{(\pm )}|\psi _{{\mathbf {q}}}^{(\pm )}\rangle = (2\pi )^3\delta (\mathrm \mathbf{q }-\mathrm \mathbf{p })\). If the potential is repulsive, the solution with outgoing spherical waves in the future is given by
while the state with incoming spherical waves in the distant past coincides with
where M(a, b; c) is a Kummer function. In particular, the squared modulus of the two given spherical waves evaluated in the origin, i.e. the probability of finding the two fermions at zero separation, is equal to
known as the Sommerfeld factor [116, 117]. Since the scattering eigenfunctions of the repulsive Coulomb Hamiltonian form a complete set of wavefunctions, they can be employed in an operatorial definition of the Coulomb Green’s functions analogous to Eq. (9),
In a way fully analogous to the one with which we have defined the Coulomb Green’s functions in Eq. (36), we introduce the full Green’s function, including both the strong and the electrostatic interactions. Therefore, we add the operator \({\hat{V}}_{\mathrm {S}} \equiv \hat{{\mathcal {V}}}^{(1)}\) to the kinetic and Coulomb potential in Eq. (36), so that
Then, we define the incoming and outcoming wavefunctions as in Ref. [27],
similar to the Eq. (38). Exploiting the operator relation \(A^{-1}-B^{-1}=B^{-1}(B-A)A^{-1}\) with \(A~=~ {\hat{G}}_{\mathrm {SC}}^{(\pm )}(E)\) and \(B~=~{\hat{G}}_{\mathrm {C}}^{(\pm )}(E)\) we find the self-consistent Dyson-like identity
that permits to rewrite the eigenstates of the full Hamiltonian in terms of the Coulomb states,
Subsequently, the scattering amplitude can be computed via the S-matrix element, given by the overlap between an incoming state with momentum \({\mathbf {p}}\) and an outcoming state \({\mathbf {p}}'\),
where \(T({\mathbf {p}}',{\mathbf {p}}) = T_{\mathrm {C}}({\mathbf {p}}',{\mathbf {p}}) + T_{\mathrm {SC}}({\mathbf {p}}',{\mathbf {p}})\) as in Eq. (4) in Ref. [118] (for the complete derivation of Eq. (47) we refer to chap. 5 of Ref. [119]). In particular \(T_{\mathrm {C}}({\mathbf {p}}',{\mathbf {p}}) = \langle {\mathbf {p}}'|{\hat{V}}_{\mathrm {C}}| \psi _{{\mathbf {p}}}^{(+)}\rangle \) is the pure electrostatic scattering amplitude and \(T_{\mathrm {SC}}({\mathbf {p}}',{\mathbf {p}}) = \langle \psi _{{\mathbf {p}}'}^{(-)}|{\hat{V}}_{\mathrm {S}}|\chi _{{\mathbf {p}}}^{(+)}\rangle \) is the strong scattering amplitude modified by Coulomb corrections. Since the eigenstates \(\psi _{{\mathbf {p}}}\) of the former are known, the scattering amplitude due only to the Coulomb interaction can be computed in closed form and admits the following partial wave expansion [27],
where \(\theta \) is the angle between \({\mathbf {p}}\) and \({\mathbf {p}}'\) and \(\sigma _{\ell } = \arg \varGamma (1+\ell +\mathrm {i}\eta )\) is the Coulomb phase shift. In particular, the strong scattering amplitude \(T({\mathbf {p}},{\mathbf {p}}')\) possesses a phase shift \(\sigma _{\ell }+\delta _{\ell }\). Furthermore, the Coulomb corrected version of \(T_{\mathrm {S}}\) can be expanded in terms of the Legendre polynomials \({\mathcal {P}}_{\ell }\) as
where \(\delta _{\ell }\) is the strong contribution to the total phase shift. After expressing the eigenstates of the full Hamiltonian in terms of the Coulomb eigenstates (cf. Eq. (46)), we concentrate on the P-wave amplitude. Since the strong interaction couples the fermions to one unit of angular momentum and Coulomb forces are central, the only nonzero component of \(T_{\mathrm {SC}}\) of the expansion in Eq. (49) is the one with \(\ell =1\). Analogously to Eq. (31) in Ref. [27], we can, thus, write
and we replace the ERE of the l.h.s. of the last equation with the \(\ell = 1\) version (cf. Ref. [37]) of the generalized effective-range expansion formulated in Ref. [36] for the repulsive Coulomb interaction,
where \(a_{\mathrm {C}}^{(1)}\), \(r_0^{(1)}\) and \(r_1^{(1)}\) are the scattering length, the effective range and the shape parameter, respectively. By comparison with the S-wave counterpart in Eq. (32) of Ref. [27], we can observe that, apart from the different power of the momentum of the incoming particles in front of the \(\cot \delta _1 - \mathrm {i}\) term, the most significant difference is provided by the polynomial on the l.h.s. of the Eq. (51), containing all the even powers of \(\eta \) from zero to \(2\ell \), as shown in Eq. (10.10) in Ref. [37]. Besides, the function \(H(\eta )\), that represents the effects of Coulomb force on the strong interactions at short distances, is given by
where \(\psi (z) = \varGamma '(z)/\varGamma (z)\) id the Digamma function. Despite the appearance, the generalized ERE is real, since the imaginary parts arising from \(H(\eta )\) cancel exactly with the imaginary part in the l.h.s. of Eq. (51). Due to the following identity on the logarithmic derivative of the Gamma function,
in fact, the imaginary part of \(H(\eta )\) proves to coincide with \(C_{\eta }^2/2\eta \). For the sake of completeness, in the case of fermion-antifermion scattering the Coulomb potential is attractive and \(H(\eta )\) in the effective range expansion (cf. Eq. (51)) should be replaced by
where \(\eta = -\alpha M/2p\) is defined as a negative real parameter.
2.2 Repulsive channel
Considering the results of the previous section, all the elements for the derivation of the Coulomb-corrected strong scattering amplitude, \(T_{\mathrm {SC}}({\mathbf {p}},{\mathbf {p}}')\), are available. Recalling the definition and Eq. (46), the amplitude can be computed by evaluating each of the terms in the expansion, whose insertions are given by retarded Coulomb propagators \({\hat{G}}_{\mathrm {C}}^{(+)}\) followed by \(\ell =1\) four-point vertices, \({\hat{V}}_{\mathrm {S}}=\hat{{\mathcal {V}}}^{(1)}\). In particular, the lowest order contribution to the T-matrix reads
where Eqs. (16) and (39)-(40) have been exploited, partial integration for the two variables has been performed and the vanishing surface terms dropped. The explicit computation of the two integrals over the free Coulomb wavefunctions (cf. Eqs. (39)–(40)) in the last row is carried out in App. C, and yields
where \(C_\eta ^2\) is the Sommerfeld factor, a function of \(\eta = \alpha M /2|{\mathbf {p}}|\). As it can be observed, the polynomial \(1+\eta ^2\) in the l.h.s. of the generalized effective range expansion appears, see Eq. (51). As shown in App. C, the P-wave strong vertex projects out of the integral all the components of the Coulomb wavefunctions \(\psi _{p}^{(\pm )}\) with \(\ell \ne 1\) appearing in the angular momentum expansion
where \(\hat{{\mathbf {p}}}\) and \(\hat{{\mathbf {r}}}\) are unit vectors parallel to \({\mathbf {p}}\) and \({\mathbf {r}} \equiv r~\hat{{\mathbf {r}}}\) respectively and \(F_{\ell }(\eta , |{\mathbf {p}}|r)\) is the regular free Coulomb wavefunction. The latter functions, derived by Yost, Wheeler and Breit in Ref. [120], display a regular behaviour in the vicinity of the origin, in contrast with the \(G_{\ell }(\eta , |{\mathbf {p}}|r)\), linearly independent solutions of the Whittaker equation for a repulsive Coulomb potential which are irregular for \(r\rightarrow 0\). Explicitly, \(F_{\ell }(\eta , |{\mathbf {p}}|r)\) has the form given in Ref. [117],
whereas the expansion for the incoming waves is obtained via the complex-conjugation property \(\psi _{{\mathbf {p}}}^{(-)}({\mathbf {r}}) = \psi _{-{\mathbf {p}}}^{(+)*}({\mathbf {r}})\). Next, we proceed with derivation of the next-to-leading order contribution to the scattering amplitude,
where partial integration has been exploited and Einstein summation convention over repeated indices is understood. More succintly, the last equation can be recast as
where in the third row, the Coulomb-corrected counterpart of the \({\mathbb {J}}_{0}\) matrix defined in Eq. (14) has been introduced,
Analogously to the \(\ell =0\) case, the higher order contributions to the T-matrix possess the same structure of Eqs. (56) and (60) differ from the latter only in the powers of \({\mathbb {J}}_{\mathrm {C}}\) and the coupling constant \(D(E^*)\). Therefore we can again write
and we can treat the terms enclosed by the round barckets as a geometric series,
Recalling the tensor product between vectors and the definition of the Coulomb Green’s function operators in Eq. (42), it is convenient to rewrite the overall matrix as
and we observe that the numerator can be considerably simplified by means of the results of App. C. In particular, Eq. (281) can be applied twice, yielding
Equipped with the last result together with Eq. (41), we recast the components of the \({\mathbb {J}}_{\mathrm {C}}\) matrix as
where the dependence of \(\eta \) on the integrated momentum \({\mathbf {s}}\) has been made explicit. As the \(\ell =0\) counterpart in Eq. (43) of Ref. [27], the integral is ultraviolet divergent. Additionally, all the off-diagonal matrix elements of \({\mathbb {J}}_{\mathrm {C}}\) vanish, as the integrand is manifestly rotationally symmetric in three dimensions except for the components \(s_i s_j\), that are integrated over a symmetric interval around zero, see Eq. (4.3.4) in Ref. [121]. In dimensional regularization, Eq. (66) can be rewritten as
an expression that in three dimensions, combined with the results in App. C, allows to simplify the Coulomb-corrected strong scattering amplitude as
in momentum space. Returning to Eq. (63) and ignoring the Feynman prescription in the denominator, we first exploit the aforementioned trick and split the integral into three parts,
While the first one proves to be finite, the other two display a pole for \(d\rightarrow 3\) and the PDS regularization scheme has to be implemented. We begin with integral in the first row of Eq. (68), \(\mathbb {j}_{\mathrm {C}}^{\mathrm {fin}}\). The numerator of the latter can be split into two parts, according to the terms of the polynomial in \(\eta \)nside the round brackets. Taking the limit \(d \rightarrow 3\), we observe that one of the two parts coincides with \(J_0^{\mathrm {fin}}\) in Eq. (45) of Ref. [27], up to a proportionality constant equal to \({\mathbf {p}}^2/3\). In comparison with the latter, the other part of \(\mathbb {j}_{\mathrm {C}}^{\mathrm {fin}}\) in Eq. (68) is suppressed by two further powers of \(\eta \), therefore it is pairwise UV-finite and the three-dimensional limit finds a justification. After these manipulations, \(\mathbb {j}_{\mathrm {C}}^{\mathrm {fin}}\) becomes
Due to spherical symmetry, the integration over the angular variables in the last term can be immediately done. By performing again the substitution \(s \mapsto 2\pi \eta = \pi \alpha M/s\), the integral in the second row of Eq. (70) can be simplified as
where \(a \equiv i\mathrm {}\pi \alpha M/|{\mathbf {p}}|\). The first of the two integrals in the last row can be evaluated by means of the following identity
connecting Euler’s Gamma function with Riemann’s Zeta function, while the second one in Eq. (70) is analogous to the integral in Eq. (46) of Ref. [27], modulo a constant factor. Considering the last two identities, Eq. (71) can be recast into
where the definition of \(H(\eta )\) in Eq. (52) and the fact that \(\zeta (2) = \pi ^2/6\) have been exploited. The subsequent addition of the last result to the already calculated contribution to Eq. (70) yields the sought closed expression for \(\mathbb {j}_{\mathrm {C}}^{\mathrm {fin}}({\mathbf {p}})\),
Now we focus on the term in the second row of Eq. (68). By comparison with the integrand of Eq. (44) of Ref. [27], we expect the integral of interest to display an UV singularity. Splitting the polynomial within the round brackets on the numerator of the integrand, we recognize, in fact, the already available \(J_{0}^{\mathrm {div}}\) in Ref. [27] whose result in the PDS scheme is given in Eq. (53) of the latter reference,
Again, spherical symmetry permits to integrate over the angular variables of the last integral in the second row of Eq. (75) and the substitution \(s \mapsto 2\pi \eta = \pi \alpha M/s\) allows for the exploitation of the integral relation between the Gamma- and the Riemann Zeta function in Eq. (72), obtaining
Unlike the first term on the r.h.s. of the last row of Eq. (75), the present integral proves to be convergent in three dimensions, since \(\zeta (2) = \pi ^2/6\) is finite and the argument of the Gamma functions are positive integers or half-integers. Additionally, no PDS poles are found in the same expression. Therefore, the limit \(d\rightarrow 3\) can be safely taken, yielding
Plugging the available result in Eq. (53) of Ref. [27], we can finally write a closed expression for \(\mathbb {j}_{\mathrm {SC}}^{\mathrm {div}, 1}({\mathbf {p}})\) in the PDS regularization scheme,
Finally, we concentrate our attention on the term in the third row of Eq. (68). From that equation, we infer that the only difference with respect to integrand of \(\mathbb {j}_{\mathrm {C}}^{\mathrm {div}, 1}\) consists in the absence of the factor \(1/s^2\), which enhances the divergent behaviour of the integral in the \(s\rightarrow +\infty \) limit. Therefore, we expect also this third contribution to \(\mathbb {j}_{\mathrm {C}}\) to be UV divergent. After splitting the integral as in Eq. (75), we obtain
Now we focus on the first term on the second row of the last equation. Rotational invariance allows again for the integration over the angular variables in d dimensions. Then, change of variables \(s\mapsto x\equiv 2\pi \eta \) permits to exploit again the multiplication identity between the Riemann Zeta and the Euler’s Gamma functions (cf. Eq. (71)). Additionally, thanks to the fundamental properties of the Gamma function and the definiton of \(\epsilon \equiv 3 -d\) we obtain
where, in the last step, the Gamma functions and the physical constants have been rewritten in order to highlight the dependence on the small quantity \(\epsilon \). From the last row of Eq. (80), we can infer that, while the Gamma function has a simple pole for \(d\rightarrow 3\), the Riemann Zeta function analytically continued to the whole complex plane is zero in that limit, since it is evaluated at a negative even integer, i.e. \(\zeta (-2n)=0\) \(n\in {\mathbb {N}}^+\). Therefore, the fourth expression in Eq. (80) cannot be immediately evaluated in the three-dimensional limit. Performing a Taylor expansion of the Zeta function about \(-2\), we obtain
where \(\zeta (3) \approx 1.20205\) is an irrational number, known as the Apéry constant. Furthermore, also the expansion of \(\varGamma \left( \frac{3-\epsilon }{2}\right) \) about 3/2 up to first order in \(\epsilon \) has to be taken into account. Combining Eq. (81) with the Taylor expansion of the physical constants with exponent \(\epsilon \) in the round bracket and the Laurent expansion of the Gamma function, Eq. (80) transforms into
where negligible terms in \(\epsilon \) have been omitted in the intermediate step. As it can be inferred from Eq. (82), the result of the integration becomes finite in the framework of dimensional regularization, even if the corresponding integral in the second row of Eq. (80) is divergent for \(d=3\) due to the singularity at \(x=0\). Since the original expression in third row of Eq. (80) contains a pole at \(d=2\) while \(\varGamma (1) = 1\) and \(\zeta (-1) = -\frac{1}{12}\) in the two-dimensional limit, the PDS correction should be taken into account. Therefore, the complete application of the PDS scheme into Eq. (82) gives
Next, we switch to the evaluation of the last term in the second row of Eq. (79). Proceeding exactly as in Eq. (80), we find
Differently from the previous case, the Riemann Zeta function is nonzero in the three-dimensional limit and the only singularity for \(\epsilon =0\) belongs to the Gamma function in the numerator of the last row of Eq. (84). Considering the expansions of all the \(\epsilon \)-dependent functions about zero, the asymptotic expression for Eq. (84) is recovered
As it can be inferred from Eq. (84), also a PDS singularity at \(d \rightarrow 2\) is present, since the Riemann Zeta function displays a simple pole at unit arguments. In particular, the Laurent expansion of the Zeta function around 1 yields
Applying the PDS regularization scheme and subtracting the correction corresponding to the \(d=2\) pole, the expression in Eq. (85) becomes
Thanks to the last expression and Eq. (87), a closed form for the third contribution to the diagonal elements of the \({\mathbb {j}}_{\mathrm {C}}\) matrix is found,
Finally, collecting the three results in Eqs. (74), (78) and (88), the latter matrix elements are obtained
A direct comparison with the \(\ell =0\) counterpart of the last expression, eqs. (47) and (53) in Ref. [27], shows that the QED contributions to \(\mathbb {j}_{\mathrm {C}}\) include terms of higher order in the fine-structure constant \(\alpha \). Moreover, owing to the elements \(\mathbb {j}_{\mathrm {C}}^{\mathrm {fin}}\) and \(\mathbb {j}_{\mathrm {C}}^{\mathrm {div},1}\), an explicit dependence on the momenta of the incoming fermions \(\pm {\mathbf {p}}\) outside \(H(\eta )\) appears. Since \(\mathbb {j}_{\mathrm {C}}\) contains quadratic terms in \({\mathbf {p}}\), Eq. (89) gives rise to a non-zero value for the effective range parameter \(r_0^{(1)}\) in the ERE formula in Eq. (51). Combining the \(\ell =1\) component of the T-matrix expansion in terms of Legendre polynomials in Eq. (49) with Eq. (68), an expression for \(|{\mathbf {p}}|^3 (\cot \delta _1-\mathrm {i})\) can be found,
Plugging the last expression into the \(\ell =1\) generalized ERE formula, the term of Eq. (89) proportional to \(H(\eta )\) cancels out with its counterpart in Eq. (51), and all the momentum-independent contributions can be collected, yielding the expression for the Coulomb-corrected \(\ell =1\) scattering length,
which represents the measured P-wave fermion–fermion scattering length. As in the \(\ell =0\) case, the ultraviolet pole is expected to be removed by counterterms which describe short-distance electromagnetic and other isospin-breaking interactions due to the differences between the quark masses [122]. The subsidiary terms will transform the coupling constant \(D(E^*)\) into a renormalization mass dependent coefficient, \(D(E^*,\mu )\), which allows for a redefinition of the scattering length as in Eq. (55) of Ref. [27],
The latter quantity is non-measurable and depends on the renormalization point \(\mu \), related to the physical scattering length through the relation
which is the \(\ell =1\) counterpart of Eq. (56) in Ref. [27]. Besides, grouping the quadratic terms in the momentum of the fermions arising in the l.h.s. of Eq. (51), an expression for the effective range is recovered,
As in the case of the inverse of the scattering length in Eq. (93), \(r_0^{(1)}\) possesses a simple pole at \(d=3\). Now the energy-dependent coefficient of our P-wave interaction \(D(E^*)\) is replaced by \(D_0\), the singularity can be removed by means of counterterms coming from the \({\mathbf {p}}^2\)-dependent \(\ell =0\) interactions, proportional to \((\psi \overleftrightarrow {\nabla }^2 \psi )^{\dagger } \psi \overleftrightarrow {\nabla }^2 \psi \) in momentum space. These interactions correspond to the term with coefficient \(C_2\) of the potential in Eq. (2) in momentum space and yield the leading contribution to the effective range in the low-momentum regime when only zero-angular-momentum interactions are present. Despite the difference in the \(\mathrm {SO(3)}\) transformation properties induced by the interaction, both the Lagrangian density with \(\ell =0\) (cf. Eq. (2)) interactions and the one with \(\ell =1\) (cf. Eq. (3)) potentials give rise to a scattering amplitude \(T_{\mathrm {S}}({\mathbf {p}},{\mathbf {p}}')\) whose \(|{\mathbf {p}}|^{2\ell +1} \cdot (\cot \delta _{\ell }~-~\mathrm {i})\) factor leads to a vanishing effective range. As soon as the Coulomb interaction is included in the Lagrangian, when the potential couples the fermions to one unit of angular momentum, a purely electrostatic non-zero effective range emerges, in contrast with the \(\ell =0\) case, see Sect. 3.3 in Ref. [27]. Therefore, we shall expect that, for higher angular momentum interactions further coefficients in the generalized expansion of \(|{\mathbf {p}}|^{2\ell +1}\cot \delta _{\ell }\) in even powers of the momentum of the fermions in the CoM frame become non-zero when the colliding particles are allowed to exchange Coulomb photons.
2.3 Attractive channel
We consider the scattering of two non-relativistic fermions with opposite charges, such as fermion-antifermion pairs. Concerning elastic scattering, the continuum eigenstates are again represented by the spherical wave solutions in Eqs. (39)–(40), with \(\eta \) now given by \(-\alpha M/|{\mathbf {p}}|\). Besides, the phenomenology of the scattering process is now enriched by the presence of bound states. In addition, annihilation is possible, but this will not be considered here. The Coulomb Green’s function, in fact, is enriched by discrete states, \(\phi _{n,\ell ,m}({\mathbf {r}})\), corresponding to bound states with principal quantum number \(n \ge 1\) and rotation group labels given by \((\ell , m)\),
where \(E_{{\mathbf {s}}}\) is equal to \(\alpha ^2 M/4\eta ^2\) and the bound state eigenvalues, \(E_n\), are given by Bohr’s formula for a system with reduced mass equal to M/2,
in natural units. As in the previous case, the Coulomb-corrected strong scattering amplitude of the elastic scattering process in configuration space takes the form
where \(\overline{D}(E^*)\) is the strong P-wave coupling constant in presence of attractive electrostatic interaction and the matrix \(\overline{{\mathbb {j}}}_{\mathrm {C}}\) is, now, given by
which corresponds to the addition of the contributions from discrete and continuum states,
and
respectively. Let us start by evaluating the term \(\overline{{\mathbb {j}}}_{\mathrm {C}}^{\mathrm {d}}\). With reference to the expression of the eigenfunctions belonging to the discrete spectrum,
where \(L_{k}^{n}(x)\) are the associated Laguerre polynomials, we first evaluate the integrals containing the gradient of the latter in the expression for \(\bar{{\mathbb {j}}}_{\mathrm {C}}^{\mathrm {d}}\) in Eq. (99), that can be performed separately for each of the wavefunctions, since the denominator does not depend on the coordinates. The application of the gradient on the bound state wavefunctions, \(\nabla \phi _{n,\ell ,m}({\mathbf {r}}) \Big |_{{\mathbf {r}}=0}\), yields
where the spherical symmetry of the Dirac delta has been exploited. Of the latter equation, we consider now the first term on the right hand side. Firstly, expressing the radius vector componentwise as a spherical tensor of rank 1 (cf. Eq. (5.24) and sec. 5.1 in Ref. [123]), the aforementioned part of Eq. (102) becomes
Now, recalling the expression of the constant term of the associated Laguerre polynomials,
Eq. (103) can be concisely recast into
where the integration over the angular variables \(\varOmega \) has been performed. After replacing the Clebsch-Gordan coefficient \((110|-m m 0)\) with \((-1)^{m+1}/\sqrt{3}\), and performing few manipulations, the sought expression is recovered,
Concerning the second term on the r.h.s. of Eq. (102), the rewriting of the gradient of a spherical harmonic into linear combination of spherical tensors (cf. Eqs. (5.24) and (5.27) in Ref. [123]) gives
thus, allowing again for an immediate integration over the angular variables,
where the Eq. (104) for the evaluation of the Laguerre polynomials at the origin has been exploited. Subsequently, the replacement \((011|0 m m) = 1\) gives the desired expression for the second term of Eq. (102),
Equipped with the results in Eqs. (106) and (109), the original integral can be immediately evaluated,
Now, taking the tensor product of the latter expression with its complex-conjugate version, as required by Eq. (99), \(\overline{{\mathbb {j}}}_{\mathrm {C}}^{\mathrm {d}}\) reduces to
Since the diagonal form of the matrix in the spherical complex basis (cf. Eq. (2.141) in Ref. [123]) is preserved in the Cartesian basis and the sum over the principal quantum number can be decomposed and evaluated in terms of the Digamma function \(\psi (z)\),
and
the contribution to the scattering matrix due to the discrete states,
can be ultimately rewritten as
As underlined in sec. 3.4 of Ref. [27], the divergent sum of the harmonic series, \(\zeta (1)\), appears in the last formula. Its presence is only due to the numerable infinity of states in the discrete spectrum, whose energy depends on the inverse square of n, while the modulus square of the gradient of the eigenfunctions evaluated at the origin yields a factor \( \propto n^2\). The replacement of \(\zeta (1)\) in Eq. (115) by its Cauchy principal value, equal to \(\gamma _E\), allows to assign a finite value to \(\overline{\mathbb {j}}_{\mathrm {C}}^{\mathrm {d}}\) and, thus, circumvent the divergence.
At this stage, we switch to the continuous contribution to the auxiliary scattering matrix, \(\overline{{\mathbb {j}}}_{\mathrm {C}}^{\mathrm {c}}\). As for the repulsive counterpart in Sect. 2.2, the possible divergences in the three-dimensional limit require the rewriting of the relevant intergrals in arbitrary complex dimension d. Therefore, the dimensionally regularized version of the second term on the r.h.s. of Eq. (98) gives
where the initial integral has been split into two parts, making use of the trick in Eq. (68). Due to the sign change in \(\eta \), the first term on the r.h.s. of Eq. (116),
can be immediately evaluated, since it coincides with Eq. (66). Therefore the result in Eq. (89) can be directly exported, rewriting Eq. (117) as
where the \(H(-\eta )\) function has been replaced by its definition in terms of the Digamma function in Eq. (52), in sight of the next developments. Subsequently, we evaluate the second term on the r.h.s. of Eq. (116), the new part of the continuum states contribution. In order to bring \({\mathbf {s}}^2\) to the denominator, we apply again the trick introduced in Eq. (68) and split the integral into three parts,
Concerning the first term on the second row of the latter equation, it vanishes in dimensional regularization, see Eq. (4.3.1a) in Ref. [121]. Therefore, we can switch to the subsequent term of Eq. (119) and apply Feynman’s trick for denominators, finding
Defining again the auxiliary variable \(\gamma = -\mathrm {i}|{\mathbf {p}}|\), we perform the momentum integration in Eq. (120),
Then, since the remaining integration over \(\omega \) turns out to be finite in two dimensions and the rest of the expression does not display any PDS singularity, we can directly reintroduce \(\epsilon \equiv 3-d\) and consider the three-dimensional limit. In particular, the integral over \(\omega \) in Eq. (121) can be evaluated in first-order approximation in \(\epsilon \), obtaining
Second, the terms depending on \(\epsilon \) in the exponent can be grouped and expanded to first order in \(\epsilon \) as in Eq. (82), whereas the Gamma function can be expressed in Laurent series up to order \(\epsilon ^0\) . Performing few manipulations and taking the \(\epsilon \rightarrow 0\) limit, the original expression in Eq. (120) becomes
Subsequently, we compute the last term on the r.h.s. of Eq. (119). As it can be inferred, the integral coincides with the one in of Eq. (123), except for an overall factor of \(\alpha ^2 M^2/4{\mathbf {p}}^2 = \eta ^2\). Therefore, its evaluation is straightforward and gives
Collecting both the results in Eqs. (123) and (124), we obtain the sought expression for \(\overline{\mathbb {j}}_{\mathrm {C}}^{\mathrm {new}}(d;{\mathbf {p}})\) in the three-dimensional limit,
We now collect all the contributions in eqs. (115), (119) and (125) and write a closed form for the diagonal matrix elements of \({\mathbb {j}}_{\mathrm {C}}\),
where the definition of \(\overline{H}(\eta )\) in Eq. (54) has been exploited and the Cauchy principal value of \(\zeta (1)\) has been taken. A direct comparison with the repulsive counterpart of the last formula in Eq. (89) shows that the map between the two expression is provided by the sign reversal in front of all the terms containing odd powers of the fine-structure constant and the replacement of \(H(\eta )\) by \(\overline{H}(\eta )\). This fact is consistent with the conclusions drawn from Eq. (70) in Ref. [27], where all the PDS-corrective terms remained unaffected by the sign change in the charge of one of the interacting fermions. We conclude this section with the derivation of an expression for the scattering length and the effective range, by making use of the attractive counterpart of the generalized effective-range expansion in Eq. (51), obtained by replacing again \(H(\eta )\) by \(\overline{H}(\eta )\) with \(\eta <0\). As a consequence of the attraction of the electrostatic interaction, the Coulomb corrections in the strong scattering parameters change sign, consistent with Eq. (126). Concerning the scattering length, we have
where the divergence can be reabsorbed by the P-wave strong coupling constant. Analogously to Eq. (72) of Ref. [27], the renormalized version of the scattering length, \(\overline{a}_{\mathrm {C}}^{(1)}(\mu )\), can be defined in terms of the physical one, \(\overline{a}_{\mathrm {C}}^{(1)}\),
Finally, the terms proportional to the square of the momentum of the fermions \({\mathbf {p}}\) give rise to a nonzero value for the effective range, as in Eq. (94),
whose divergent part, in case the energy-dependent coefficient of the \(\ell =1\) interaction \(D(E^*)\) is replaced by \(D_0\), can be again reabsorbed by counterterms coming from \({\mathbf {p}}^2\)-dependent \(\ell =0\) interactions.
3 The finite-volume environment
At this stage, we transpose the physical system of non-relativistic spinless fermions interacting via Coulomb photons onto a cubic spatial volume with edges of length L. In this environment, it is customary to continue analytically the fields and the wavefunctions outside the box by means of periodic boundary conditions (PBCs). It follows that a free particle subject to PBCs carries a momentum \({\mathbf {p}}=2\pi {\mathbf {n}}/L\), where \({\mathbf {n}}\) is a dimensionless three-vector of integers. In numerical simulations, the finite-volume configuration space is even discretized, so that for each direction only N points separated by a spacing a are considered and the cubic box reduces to a cubic lattice. Unlike QCD fields, the photon field in QED is truncated and modified by the boundary of the volume. In particular, when PBCs are implemented, the validity of Ampère’s and Gauss’s law is compromised. The problem is circumvented by introducing a uniform background charge density, a procedure that proves to be equivalent to the removal of the zero modes of the photon [65, 94]. Once the latter are canceled, the Coulomb potential between two identical charges e becomes (cf. Fig. 4)
where the \({\mathbf {n}} \in {\mathbb {Z}}^3\) encodes the dimensionless finite-volume momenta. Discarding the zero modes, the latter are restricted to \(|{\mathbf {p}}| \ge 2\pi /L\), whereas the viability of a perturbation treatment of QED is controlled by the parameter \(\eta = \alpha M /2|{\mathbf {p}}|\), which scales as the inverse of the momentum of the interacting particles. Combining the above constraint with the definition of \(\eta \), it follows that \(\eta \sim \alpha M L\) and the photon field insertions can be treated perturbatively if \(ML \ll 1/\alpha \). As \(\eta \) grows linearly with the spatial volume, for any value of M exists a critical value of L that regulates the applicability of perturbation theory. Besides the condition \(\eta \ll 1\), we assume henceforth the limit \(M \gg 1/L\), since for the current Lattice QCD calculations large volumes are employed [94].
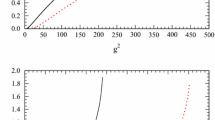
Behaviour of the finite-volume Coulomb potential energy between unit charges along an axis parallel to an edge of the cube (solid curve) obtained from \(V_{\mathrm {C}}^L({\mathbf {r}})\) in Eq. (130) and the infinite volume Coulomb potential \(V_{\mathrm {C}}({\mathbf {r}})\) (dashed curve) [40, 94], whose Fourier transform with IR regulator is presented in Eq. (28)
Furthermore, the finite volume QED effects are such that the energy eigenvalues of two charged fermions (e.g. hadrons) are modified in the same way by their self-interactions and by their interactions with each other, and the shifts take the form of power laws in L [40]. As a consequence, in the presence of Coulomb photons the kinematics of two-body processes receives power law modifications in the finite volume context [40, 48]. In particular, if the infinite-volume effective range expansion for the P-wave scattering is rewritten in terms of the center of mass energy,
then \(E^* = 2M + T\) in the above expression is replaced by its finite volume counterpart.Footnote 2 Equation (131) thus becomes
The original dependence of the r.h.s. of the last equation on the powers of the finite volume kinetic energy \(T^L = E^{*L}-2M^L\) can be restored by exploiting the expression of the finite-volume shift for the masses of spinless particles with unit charge in Eqs. (6) and (19) of Ref. [40],
where the sum of the three-dimensional Riemann series regulated by the spherical cutoff \(\varLambda _n\) is denoted with \({\mathcal {I}}^{(0)} \approx -8.913632\) (cf. App. D.1). To this purpose, primed scattering parameters are introduced
and
differing from the infinite volume counterparts by corrections of order \(\alpha \) and scaling as the inverse of the box size. Explicitly, the infinite volume ERE in Eq. (132) rewritten in terms of the translated parameters in Eqs. (134)–(138) for unbound states with \(T^L = {\mathbf {p}}^2/M\) assumes the form
where the changes in the total energy have been incorporated in the primed scattering parameters. Finally, also the validity region of the last expansion is modified by the cubic finite-volume environment, due to the changes in the analytic structure of the scattering amplitude in the complex \(|{\mathbf {p}}|\) plane. The absence of the zero mode in the Coulomb potential in Eq. (130), in fact, yields a shift in the branch cut of the imaginary \(|{\mathbf {p}}|\) axis from the origin to \(\sqrt{2\pi M/L} + {\mathcal {O}}(1/M)\), which fixes the inelastic threshold for the two-hadron state (cf. fig. 2 in Ref. [94]).
The last version of the ERE, combined with the quantization conditions discussed below, will turn out to be the key ingredient for the derivation of the finite volume energy corrections for scattering and bound states with one unit of angular momentum.
3.1 Quantization condition
After introducing the finite and discretized configuration space, we derive the conditions that determine the counterpart of the \(\ell =1\) energy eigenvalues in the cubic region. These states transform as the three-dimensional irreducible representation \(T_1\) (in Schönflies’s notation [124]) of the cubic group [61,62,63], the finite group of the 24 rotations of the cube that replaces the original SO(3) symmetry in the continuum and infinite volume context [60].
As it can be inferred from Eq. (43), the eigenvalues of the full Hamiltonian of the system \({\hat{H}}_0 +{\hat{V}}_{\mathrm {C}}+{\hat{V}}_{\mathrm {S}}\) can be identified with the singularities of the two-point correlation function \(G_{\mathrm {SC}}({\mathbf {r}},{\mathbf {r}}')\) and are called quantization conditions in the literature [69,70,71, 94]. The Green’s functions \(G_{\mathrm {SC}}({\mathbf {r}}',{\mathbf {r}})\) in turn can be computed from the terms in the expansion over the P-wave interaction insertions stemming from Eq. (45), with \({\hat{V}}_{\mathrm {S}}\) in momentum space given in Eq. (6). In particular, the three lowest order contributions in \(D(E^*)\) yield, respectively,
and
Extending the calculation to higher orders, the expression of \((N+1){\mathrm {th}}\) order contribution to the full two-point correlation function can be derived,
thus allowing to rewrite the original Green’s function in terms of a geometric series of ratio
that we identify as \({\mathbb {j}}_{\mathrm {C}}\) (cf. Eq. (64)),
where
can be interpreted as a source and a sink coupling the fermions to a P-wave state, respectively. As in the \(\ell =0\) case, the pole in the second term of Eq. (144) permits to express the infinite-volume quantization conditions,
where the identity matrix multiplied by the CoM energy dependent coupling constant is equal to the inverse of the matrix of the double derivatives of the Coulomb two-point Green’s function evaluated at the origin, \({\mathbb {j}}_{\mathrm {C}}\). Concentrating again on the retarded two-point correlation function and adopting the notation of Ref. [94], the finite-volume counterpart of Eq. (144) becomes
Similarly, the pole in the second term on the r.h.s. of Eq. (146) yields the finite-volume quantization condition,
that determines the \(T_1\) eigenvalues. As in the \(\ell =0\) case, we proceed by expanding \(G_{\mathrm {C}}^{(+),L}({\mathbf {r}}_i, {\mathbf {r}}_{i+1})\) in powers of the fine-structure constant and truncate the series to order \(\alpha \). Moreover, we notice that the directional derivatives of the two-point Coulomb Green’s function evaluated at the origin correspond to the pairwise closure of the external legs of the Coulomb ladders in the expansion of \(G_{\mathrm {C}}^{(+)}\) in Fig. 2 to two-fermion vertices, evaluated at the origin in configuration space. As a consequence, the matrix elements of \({\mathbb {j}}_{\mathrm {C}}^L\) can be interpreted as bubble diagrams with multiple Coulomb-photon insertions inside. Analytically, the two lowest order contributions to \({\mathbb {j}}_{\mathrm {C}}\), that correspond to bubble diagrams, respectively with and without a Coulomb-photon insertions, read
where the Dyson identity between \({\hat{G}}_{\mathrm {C}}^{(\pm )}\) and \({\hat{G}}_{0}^{(\pm )}\) (cf. Eq. (37)) has been exploited and \(\varepsilon \) has been set to zero. Replacing again the integrals over the momenta by sums over the dimensionless momenta \({\mathbf {n}},{\mathbf {m}}\in {\mathbb {Z}}^3\), the finite-volume counterpart of Eq. (148) is obtained,
where the finite-volume mass \(M^L\), the speherical cutoff \(\varLambda _n\) and the dimensionless CoM momentum of the incoming particles \({\tilde{p}} = L|{\mathbf {p}}| / 2\pi \) have been reintroduced. With the aim of regulating the sums in Eq. (149) for numerical evaluation while maintaining the mass-independent renormalization scheme (cf. sec. II B of Ref. [94]), we are allowed to rewrite the finite volume quantization conditions as
where \({\mathbb {j}}_{\mathrm {C}}^{\{\varLambda \}} ({\mathbf {p}})\) and \({\mathbb {j}}_{\mathrm {C}}^{\{\mathrm {DR}\}} ({\mathbf {p}})\) denote the \({\mathcal {O}}(\alpha )\) approximations of \({\mathbb {j}}_{\mathrm {C}}\) computed in the cutoff- and dimensional regularization schemes. Starting again from Eq. (148), we insert the spherical cutoffs as in its discrete counterpart (cf. Eq. (149)), in sight of the evaluation of \({\mathbb {j}}_{\mathrm {C}}^{\{\varLambda \}}\),
where \(S_{\varLambda }^2\) denotes the three-dimensional sphere with radius \(\varLambda \). Isolating the \({\mathcal {O}}(\alpha )\) contribution, we obtain
where the isotropy of the cutoff has been exploited in the second step and \({\mathcal {O}}(\varLambda ^0)\) denotes constant or vanishing terms in the \(\varLambda \rightarrow +\infty \) limit. Concerning the \({\mathcal {O}}(\alpha )\) term, the integral can be simplified as follows
where \(\varXi _1 \equiv (1-\omega ){\mathbf {q}}^2 -\omega {\mathbf {p}}^2\) and Feynman parametrization for the denominators has been applied. The subsequent integration over the momentum \({\mathbf {k}}\) through Eq. (B17) in Ref. [113] and the exploitation of rotational symmetry in the outcoming integrand (cf. Eq. (4.3.1a) in Ref. [121]) gives
Then, it is convenient to split the integrand of Eq. (154) into two parts and to simplify the numerator,
where \({\mathfrak {J}}_1\) (\({\mathfrak {J}}_2\)) corrresponds to the first (second) integral on the l.h.s. of the last equation and it will generate the leading contributions in \(\varLambda \). Beginning with the latter term, integration over the momentum \({\mathbf {l}}\) yields
where \(\varXi _2\) is an ancillary variable,
Exploiting the fact that \({\mathbf {p}}/\varLambda \ll 1\), the integrand in the latter expression can be considerably simplified. Exploting the results
and
the remaining integration can be performed, obtaining the desired expression for \({\mathfrak {I}}_1\)
Concerning the \({\mathfrak {I}}_2\) term, its rotational symmetry and integration over the angular variables permits to split it in turn into two terms,
Considering the first term on the r.h.s. of Eq. (160), integration over the radial momentum yields again an \(\mathrm {arccoth}(x)\) function, which is eventually responsible of a further logarithmic divergence in the UV region,
Approximating the expression again under the assumption \({\mathbf {p}}/\varLambda \ll 1\) and performing the integration over \(\omega \) (cf. Eq. (157)), the expression on the r.h.s. of Eq. (161) become
i.e. it carries the second logarithmic contribution to \({\mathbb {j}}_{\mathrm {C}}^{\{\varLambda \}}\) to order \(\alpha \) in the perturbative expansion. Finally, we consider the second term on the r.h.s. of Eq. (160) and introduce the auxiliary variables \(\gamma ^2 \equiv -{\mathbf {p}}^2\) and \(\varXi _3 \equiv \gamma ^2/(1-\omega )\). The integration over the radial momentum \(|{\mathbf {q}}|\) yields
an expression that can be simplified in the large coutoff limit, \({\mathbf {p}}/\varLambda \ll 1\), obtaining
Although the remaining integral is unbound, the overall expression is independent of the cutoff \(\varLambda \), therefore it can be neglected as the whole \({\mathcal {O}}(\varLambda ^0)\) contributions. This divergence is analogous to the one found in the \(\ell =0\) case, and turns out to disappear if a translation in the momenta such as \({\mathbf {k}} \mapsto {\mathbf {k}} - {\mathbf {q}}\) in the original expression of the \({\mathcal {O}}(\alpha )\) term of \({\mathbb {j}}_{\mathrm {C}}^{\{\varLambda \}}\) in Eq. (151) is performed. Now, collecting the results in Eqs. (152) and (159), the cutoff-regularized version of \({\mathbb {j}}_{\mathrm {C}}\) is obtained to the desired order in the fine-structure constant,
where the \({\mathcal {O}}(\varLambda ^0)\) contributions have been discarded. Now we proceed with the calculation in dimensional regularization of \({\mathbb {j}}_{\mathrm {C}}\). To this purpose, it is convenient to start from the exact expression of \({\mathbb {j}}_{\mathrm {C}}\) to all orders in \(\alpha \) in arbitrary d dimensions (cf. Eq. (65)),
where the integrand has been expanded up to the first order in \(\alpha \). In particular, the \(\alpha \)-independent contribution in Eq. (166) gives
where the rotational invariance of the integrand has been exploited and \(\varepsilon \) has been set to zero. Since the integrand is a polynomial in the momentum, the first contribution in the second row of the last equation vanishes in dimensional regularization, whereas the remaining term turns out to coincide with the purely strong counterpart of \({\mathbb {j}}_{\mathrm {C}}(d;{\mathbf {p}})\) in Eq. (18),
thus is finite and the limit \(d \rightarrow 3\) can be safely taken, obtaining
Due to the presence of the imaginary unit in the r.h.s. of the last equation, it turns out that the \(\alpha \)-independent component of \({\mathbb {j}}_{\mathrm {C}}^{\{\mathrm {DR}\}}\) does not contribute in Eq. (150), since only real parts are retained. Regarding the \({\mathcal {O}}(\alpha )\) term of \({\mathbb {j}}_{\mathrm {C}}\) in arbitrary dimension, the integral can be recast as
where \(\gamma \equiv -\mathrm {i}|{\mathbf {p}}|\) and the Feynman parametrization for the denominators has been adopted. The subsequent momentum integration in the latter yields
where the renormalization scale \(\mu \) has been introduced. Conversely, the first term in the second row of Eq. (170) vanishes like the first integral on the r.h.s. of Eq. (167). Introducing the small quantity \(\epsilon = 3-d\), the integral over \(\omega \) can be computed to first order in \(\epsilon \), obtaining
Exploiting the result in the last formula, Eq. (170) partially expanded to order \(\epsilon \) becomes
Expanding in turn the Gamma function and the power term \(\mu \sqrt{\pi }/\gamma \) in Laurent and Taylor series, respectively, and truncating the expansion to order \(\epsilon ^0\), the desired expression for \({\mathbb {T}}_{\mathrm {SC}}({\mathbf {p}})\) in dimensional regularization is recovered
Then, we bring further simplification to the finite volume quantization condition by taking the trace of Eq. (150),
thus transforming a matrix identity into a scalar one as the one for S-waves. Finally, we take the real part of the expressions in Eqs. (165) and (173) and replace the fermion mass by its finite-volume couterpart, obtaining the regulated version of the finite volume quantization condition (cf. Eq. (147)) in explicit form,
Thanks to the last identity, the finite-volume version of the effective range expansion in Eq. (139) can be rewritten in an explicit form. Besides, we drop in the next developments of the derivation the pole \(1/\epsilon \) arising from dimensional regularization, since it does not deliver information on the energy eigenvalues of our two-body system.
3.2 Finite volume effective range expansion
First of all, we concentrate on the infinite volume version of the effective range expansion. By inserting the expression of \(T_{\mathrm {SC}}\) given in Eq. (66) into Eq. (51) and exploiting the closed form of \(\mathbb {j}_{\mathrm {C}}\) in dimensional regularization to all orders in \(\alpha \) given in Eq. (89) we obtain a relation between the P-wave phase shift and the strong coupling constant \(D(E^*)\) in the presence of Coulomb photon exchanges,
Since the asymptotic behaviour of the momentum integrals in the ultraviolet region is left invariant by discretization, Eq. (177) can be straightforwardly adapted to the cubic finite-volume case, provided the infinte volume parameters are replaced by finite volume ones,
which is valid to all orders in the fine-structure constant. Now, the quantization conditions derived in the previous section can be exploited by replacing the inverse of the finite-volume strong-coupling constant with the expression in Eq. (175). Thus, the following equation is obtained,
Similarly to the \(\ell =0\) case, we notice that the finite-volume mass of the fermions is multiplied by the fine-structure constant in all the occurrences. It follows that, in the \({\mathcal {O}}(\alpha )\) approximation of the Coulomb Green’s functions and their derivatives, we can consistently ignore the leading-order corrections to \(M^L\) and replace the latter with M, at least in Eq. (179). Nevertheless, we account for the QED power law modifications of the masses [40] in the finite-volume version of the effective-range expansion in Eq. (51) by means of the shifted scattering parameters (cf. Eqs. (134)–(138)),
where the ellipsis stands for higher-order scattering parameters. Combining the latter expression with Eq. (139) and isolating the regulated sums, we obtain the desired explicit version of the effective-range expansion to order \(\alpha \),
in terms of the Lüscher functions,
and
In particular, the \({\tilde{p}}\)-independent Lüscher sum in Eq. (182) vanishes, as shown in App. D.1, whereas \({\mathcal {S}}_3(\tilde{{\mathbf {p}}})\) generates the new series of double sums to be computed in the low-\({\mathbf {p}}\) limit.
3.3 Approximate energy eigenvalues
Since the Sommerfeld factor is not a rational function of the momentum of the colliding particles in the CoM frame, a non-perturbative counterpart in \(\alpha \) of the Eq. (181) in the low-momentum limit would allow only numerical solutions for \({\mathbf {p}}^2\), which lie beyond our purpose. Nevertheless, under the hypothesis that the expansions are perturbative in 1/L times the length scale characterizing the strength of the interaction, governed by the scattering parameters, and assuming that \(ML \ll 1/\alpha \), the Coulomb photon insertions in the diagrams can be treated perturbatively. Under these conditions, the approximate expression of the ERE presented in Eq. (139) can be exploited for an analytical derivation of the finite volume corrections to the energy eigenvalues.
3.3.1 The lowest unbound state
Differently from the S-wave case in sec. III D of Ref. [94], the perturbative expansion of the arguments of the summations in the Lüscher functions around zero finite-volume momentum \({\tilde{p}}\), corresponding to a total energy equal to 2M now looses significance, due to symmetry reasons. Given that \(\ell =1\) states in the continuum and infinite volume are mapped to \(T_1\) states in a finite cubic finite volume, the latter are expected to be three-fold degenerate. While the multiplicity of the zero energy scattering state is one, its nearest neighbour with \(|\tilde{{\mathbf {p}}}| = 1\) is six-fold degenerate with total energy equal to \(2M + 4\pi ^2/ML^2\), thus making it a suitable candidate for both \(T_1\) and \(T_2\) eigenstates. Moreover, if the box size is large enough, the momentum \(|{\mathbf {p}}| = 2\pi /L\) is small, the effective-range expansion in the l.h.s. of Eq. (181) remains valid and can be truncated at any power of \({\mathbf {p}}^2\). Otherwise, the non-perturbative approach in sec. 2.5 of Ref. [69] needs to be considered, and the energy eigenvalues would be expressed in terms of the phase shift \(\delta _1\). Following the small-momentum approach, we expand the Lüscher functions in Eqs. (182)–(184) in Taylor series about \({\tilde{p}}^2 = 1\) and retain only small or negative powers of the quantity \(\delta {\tilde{p}}^2\equiv {\tilde{p}}^2 -1\). Concerning the Lüscher function \({\mathcal {S}}_1({\tilde{p}})\), the approximation yields
where the dots denote terms of order \((\delta {\tilde{p}}^2)^6\) and the large \(\varLambda _n\) limit is understood. In the notation of App. D and Ref. [94], Eq. (185) is concisely recast into
where the sums of the implied three-dimensional Riemann series are reported in App. D.1. Regarding the function \({\mathcal {S}}_2({\tilde{p}})\), we proceed by isolating and expanding the double sums with \(|{\mathbf {n}}|\) or \(|{\mathbf {m}}|\) equal to one,
The subsequent expansion of the argument of the two series in the same fashion of Eq. (185) shows that all the resulting sums converge in the infinite-\(\varLambda _n\) limit. Therefore, we are allowed to remove the spherical cutoff and the two double sums in Eq. (187) merge, yielding
where, differently from the ones in the appendix of Ref. [94], the series \(\chi _i\) with \(i \ge 1\) include \({\mathbf {n}} = {\mathbf {0}}\) and are defined as
Furthermore, the expansion of the remaining term of the Lüscher function \({\mathcal {S}}_2\) leads to results in analogous to the ones of the S-wave case,
where the ellipsis stands for terms of order \((\delta {\tilde{p}}^2)^3\). The \({\mathcal {R}}^{(1)}\) and \({\mathcal {R}}_{ij}^{(1)}\) sums in the last equation coincide with the P-wave counterparts of the sums in Eqs. (A6) and (A9) in Ref. [94], namely
and
with \(i,j \ge 2\) and \(i+j \ge 6\), which are invariant under permutation of the lower indices, \({\mathcal {R}}_{ij}^{(1)} = {\mathcal {R}}_{ji}^{(1)}\), and convergent for \(i,j \ge 1\) and \(i+j > 2\). Exploiting the symmetry property under index exchange and combining the results in Eqs. (191) and (192), we find the desired result
Subsequently, we treat the genuinely new Lüscher function, \({\mathcal {S}}_3({\tilde{p}})\). To this purpose, we decompose the initial double series into three pieces,
where a subsidiary spherical cutoff \(\varLambda _m\) has been introduced in order to highlight the divergent nature of the three terms. In particular, the first and the second contribution to \({\mathcal {S}}_3({\tilde{p}})\) on the r.h.s. of the last equation, can be recast as
where the dots denote terms of order \((\delta {\tilde{p}}^2)^3\), while the non-symmetric and divergent generalizations of \(\chi _0\) in Eq. (283) and of \({\mathcal {R}}_{ij}^{(1)}\) in Eq. (192) have been introduced,
and
respectively. Quite similarly, the third contribution to \({\mathcal {S}}_{3}({\tilde{p}})\) in Eq. (194) can be subdivided and expanded as follows
where the two terms involving single sums can be, in turn, expanded in pairs, obtaining
where the neglected terms are again of order \((\delta {\tilde{p}}^2)^3\) and for the resulting convergent series the limit \(\varLambda _n, \varLambda _m\rightarrow +\infty \) is understood. On the other hand, this limit can not be taken for the non-regularized counterpart of \({\mathcal {I}}^{(1)}\),
whose divergence will cancel with the one from \({\mathcal {P}}^{(1)}\) in Eq. (196). Secondly, the expansion of the double sum in Eq. (198) yields the appearance of further \({\mathcal {P}}_{2i~2j~2k}^{(1)}\) terms,
Collecting the expansions of the three contributions in Eqs. (199) and (201) we can finally write
Now, the two partial results in Eqs. (195) and (202) can be summed together, obtaining the sought expression of \({\mathcal {S}}_3({\tilde{p}})\) as a power series in \(\delta {\tilde{p}}^2\). In particular, we notice that the sum of all the series appearing at each order in \(\delta {\tilde{p}}^2\) has to be finite in the limit \(\varLambda _n,\varLambda _m\rightarrow +\infty \), irrespective of the convergent or divergent behaviour of each individual sum. In particular, we observe that the latter limit can be directly taken to all orders in the small quantity, with the only exception of the sums in the \(\delta {\tilde{p}}^2\)-independent contribution, that are regularized quadratically in the cutoff \(\varLambda _n\). As a consequence, we can simplify our \(\delta {\tilde{p}}^2\)-expansion for \({\mathcal {S}}_3({\tilde{p}})\) by grouping the divergent sums order by order and defining the finite coefficients



and

where the polynomials \(q_S({\mathbf {n}},{\mathbf {m}})\) and \(q_X({\mathbf {n}},{\mathbf {m}})\) are defined as
and
Equipped with the definitions in Eqs. (203)–(206), we can write compactly the final expression for the expansion of \({\mathcal {S}}_3({\tilde{p}})\) in terms of convergent sums up to the quadratic order in \(\delta {\tilde{p}}^2\),

After redefining the regularized sum in Eq. (193) through the addition of the last term on the r.h.s. of Eq. (181),
we plug the expressions in Eqs. (186), (195), (196) and (209) in the finite volume effective range expansion and obtain

where the shifted higher-order scattering parameters \({r_{2}'}^{(1)}\) and \({r_{3}'}^{(1)}\) on the l.h.s. of the last equation have been included, see Eqs. (134) and (138). The subsequent multiplication of the last equation by the scattering length permits to introduce coefficients identical to the ones in Eq. (37) of Ref. [94],
modulo an overall damping factor \(\xi \equiv 4\pi ^2/L^2\). If the scattering parameters are small and of the same magnitude of 1/L as in the S-wave case, the importance of the auxiliary parameters just introduced can be quantitatively assessed. In particular, by assigning one unit of ’weight’ for each scattering parameter in the effective-range expansion and one unit for 1/L, we find that, neglecting the fine-structure constant, the largest parameter is \(d_1\) (order three), followed by \(d_0\) and \(d_2\) (order four), whereas the constants \(d_3\), \(d_4\) and \(d_5\) are of order six, eight and ten respectively. With the aim of finding a perturbative formula exact to third order in \(d_0\), we observe that in the final expression for the squared momentum shift \(\delta {\tilde{p}}^2\), only terms of order smaller or equal to twelve in 1/L and in the scattering parameters should be retained. This fact justifies the inclusion of the above higher order scattering parameters in the effective range expansion in Eq. (211). Furthermore, rewriting \({\tilde{p}}^2\) in the latter equation as \(\delta {\tilde{p}}^2+1\), the approximated effective range expansion can be rewritten as a power series of the squared momentum shift,

Due to the smallness of \(\delta {\tilde{p}}^2\), contributions multiplied by higher positive powers of the finite-volume momentum are increasingly suppressed. It follows that the dominant finite volume corrections are expected to be found by solving the truncated version of Eq. (213) to order zero in \(\delta {\tilde{p}}^2\),

Solving the last equation for \(\delta {\tilde{p}}^2\) and expanding the denominator up to order twelve in the small constants, we find

Denoting the outcome of the first iteration as \(\delta {\tilde{p}}^2_0\), we proceed with an improvement of the last result by plugging the latter into the term proportional to \(\delta {\tilde{p}}^2\) of the expansion in Eq. (213) truncated to the terms quadratic in the squared momentum shift,

Solving the last equation and retaining only terms up to order twelve in 1/L and the scattering parameters, we obtain a refined version of the momentum shift,

in which the new contributions appearing at each order in the auxiliary constants (cf. Eq. (215)) have been isolated. Restoring the dimensional constants in the momenta, the energy of the lowest \(T_1\) scattering state can be now obtained in few steps,

where the ellipsis stands for terms of higher order in the scattering and 1/L parameters and in the fine-structure constant. Besides, all the terms on the r.h.s of the last equation with the only exception of the first represent the modifications of a free \(T_1\) finite-volume state with energy \(\xi /M\) induced by the strong and the electromagnetic interactions. Analogously to the \(\ell =0\) case, only the interplay between strong and electromagnetic forces generates the linear corrections in \(\alpha \), and the leading QED corrections are of the same order of the modifications due to the QCD forces alone. By comparison with the S-wave counterpart of Eq. (218) (cf. Eq. (37) in Ref. [94]), we observe that contributions from higher order scattering parameters such as \({r_{2}'}^{(1)}\) and \({r_{2}'}^{(1)}\) begin to appear, whereas all the terms arising from \({r_{3}'}^{(1)}\), included in the original version of the ERE, vanish in the order twelve expansion in the scattering parameters. Furthermore, by explicit computation it can be proven that the subsequent iteration step for the improvement of the squared momentum shift, \(\delta {\tilde{p}}_4^2\), does not lead to the appearance of further addend on the r.h.s. of Eq. (218) in the chosen approximation scheme. Finally, we conclude the treatment by isolating the corrections in the last equation and restoring the infinite volume scattering parameters,

where the differences with respect to Eq. (218) involve only the linear term in the fine-structure constant and are proportional to \({\mathcal {I}}^{(0)}\).
3.3.2 The lowest bound state
As hinted in the preamble, some observed lines in the hadron spectrum such as the Y(4626), Y(4630) and Y(4660) [95] or the \(P_c^+(4380)\) and \(P_c^+(4450)\) [100, 103] are susceptible to the interpretation as two-body bound states between lighter colorless quark compounds with one unit of orbital angular momentum.
Therefore, it remains instructive to study the lowest two-fermion \(T_1\) bound state, by switching to imaginary momenta \({\mathbf {p}}=\mathrm {i}\varvec{\kappa }\), where \(\kappa = |\varvec{\kappa }|\) represents the imaginary part of the momentum. To this purpose, we rewrite the FV effective range expansion in Eq. (181), truncated on the l.h.s. to the sextic term in the binding momentum,
First, we consider the limit of large finite-volume binding momentum, \({\tilde{\kappa }} = |\tilde{\varvec{\kappa }}| \gg 1\), which corresponds to a tightly-bound state. Thus, an approximation for the Lüscher functions in this regime becomes necessary. In particular, we observe that the asymptotic behaviour of \({\mathcal {S}}_1(\mathrm {i}{\tilde{\kappa }})\) and \({\mathcal {S}}_2(\mathrm {i}{\tilde{\kappa }})\) is already available in literature and gives,
and
see eqs. (43,44) in Ref. [94], respectively. On the other hand, the large binding energy limit of \({\mathcal {S}}_3(\mathrm {i}{\tilde{\kappa }})\) requires a new derivation, presented in detail in App. (E),
Recalling the fact that \({\mathcal {S}}_0({\tilde{\kappa }}) ) = \varUpsilon = 0\) (cf. Eq. (283)) and collecting the results in Eqs. (221)–(223), the above finite volume effective range expansion becomes,
Second, we highlight the dependence on the fine-structure constant in the last equation by rewriting the binding momentum in a power series,
where \(\kappa _0\) results from strong interactions alone and the subscript corresponds to the power of \(\alpha \) on which each term in the expansion depends. Replacing in Eq. (224) the shifted scattering parameters with the infinite volume ones in Eqs. (134)–(138) and discarding all the terms of order \(\alpha ^2\) or higher in the expansions, Eq. (224) transforms into
Grouping all the terms independent on \(\alpha \), we observe that the following equality
holds, since the remaining terms in Eq. (226) depend linearly on \(\alpha \). Therefore, an expression for \(\kappa _1\) can be drawn from the original Eq. (226) by dropping the terms listed in Eq. (227),
In particular, retaining only the terms depending on the two lowest order scattering parameters as in the zero angular momentum case (cf. Eqs. (45)–(46) in Ref. [94]), a more approximated expression for \(\kappa _1\) in terms of \(\kappa _0\), \(a_{\mathrm {C}}^{(1)}\) and \(r_0^{(1)}\) can be obtained,
From the latter equation the first two terms generate finite-volume corrections, whereas the third one introduces QED modifications to the unperturbed binding momentum \(\kappa _0\) which do not vanish in the infinite volume limit. Now, considering the binding energy of the lowest \(T_1\) state in the linear approximation in \(\alpha \),
and substituting the simplified expression of \(\kappa _1\) in Eq. (229), we find an approximate expression for the energy of the lowest \(T_1\) bound state,
where the first two terms represent the infinite volume binding energy up to \({\mathcal {O}}(\alpha )\), while the third contribution vanishes for \(L \rightarrow +\infty \) together with the fourth one. Furthermore, if \(r_0^{(0)}\) is small enough, the denominator in the second and in the fourth term of the last equation can be expanded in powers of \(r_0^{(0)}/\kappa _0 \ll 1\) and the leading order mass shift for tightly-bound \(T_1\) two-body states eventually becomes,
From the r.h.s. of the last expression we can infer that the leading QED corrections to \(E_{B}^{(1,T_1)}(L)\) presented in Eq. (232) are positive (\({\mathcal {I}}^{(0)} <0\), see Eq. (299)), analogously to the LO mass shifts for \(\ell =1\) states of two-body systems with strong interactions alone in Eq. (53) of Refs. [66, 72]. Also noteworthy is the fact that, when compared to the S-wave case in Eq. (46) in Ref. [94], the sign of the P-wave shift is reversed while the magnitude remains unchanged. As discussed in Refs. [66, 72], the significance of this behaviour can be traced back to the spatial profile of the \(\ell =0\) and \(\ell = 1\) two-body wavefunctions associated to the considered bound eigenstates. Qualitatively, the relationship found between the two finite volume energy corrections means that zero angular momentum states are more deeply bound when embedded in a finite volume, while the counterpart with one unit of angular momentum are less bound. In conclusion, together with the derivation of \(\varDelta E_{B}^{(1,T_1)}\), we have simultaneously proven that the addition of a long-range force on top of strong forces in two-fermion systems within a cubic finite-volume produces changes of the same magnitude on S- and P-wave bound energy eigenvalues.
4 Outlook
Before drawing the conclusions of our work, we qualitatively outline the possible improvements to the above analysis. There are two main directions for the generalization of the present study. These consist in the inclusion of transverse photons in the Lagrangian density of the system and in the treatment of strong interactions with higher angular momentum couplings.
Let us start from the former. Thanks to their vector nature, transverse photons can couple to the fermionic fields in several different ways, see Eq. (26). Among these, here we retain only the Dipole vertex (cf. App. A), which is expected to yield the leading-order contributions to the T-matrix and the full Green’s function. As we previously hinted, these photons, denoted by wavy lines, can propagate also between different bubbles. Consequently, at each order in \(D(E^*)\) a numerable infinity of new diagrams with different topologies and transverse-photon exchanges inside and outside the bubbles appears. Unfortunately, part of the amplitudes associated to these diagrams can not be written as powers of the loop (bubble) integrals, since the transverse photons propagating outside the fermion loops introduce a correlation between the bubbles (cf. fig. (4) in Ref. [94] and Fig. 5). It follows that an expression for the T-matrix element of the two-body scattering process, \(T_{\mathrm {SCT}}\), written in terms of a geometric series of ratio proportional to the interaction strength, \(D(E^*)\), can not be found. More formally, a self-consistent rewriting of the full Green’s function operator \({\hat{G}}_{\mathrm {SCT}}\) in the form of a self-consistent equation à la Dyson separating the QED Green’s function operator, \({\hat{G}}_{\mathrm {CT}}\), from the strong interaction operator \({\mathcal {V}}^{(1)}\) (cf. Eq. (45)) does not exist. These facts prevent the exact determination of \(T_{\mathrm {SCT}}\) to all orders in the fine-structure constant.
The dressed strong vertex coupling to one unit of angular momentum as a superposition of the original fermion-fermion interaction vertex plus a numerable infinity of tree-level and bubble diagrams containing one transverse-photon exchange. The ellipses represent other diagrams featuring one or more strong vertices and single transverse-photon insertions
Nevertheless, the gapped nature of the momentum in the finite-volume environment allows for a perturbative treatment of the whole non-relativistic QED. Therefore, approximate expressions for \(T_{\mathrm {SCT}}\) that incorporate the effects of the transverse photons up to the desired order in \(\alpha \) can be derived.
One of these approaches consists in writing the infinite-volume T-matrix element \(T_{\mathrm {SCT}}\) exactly as \(T_{\mathrm {SC}}\) in Eq. (68) with \(D(E^*)\) at the denominator replaced by a dressed strong P-wave coupling constant \(D_{\mathrm {T}}(E^*)\), that includes the effects of transverse photons up to first order in the fine-structure constant. Analytically, this energy-dependent constant can be derived by evaluating the contributions of all the possible bubble diagrams with one tranverse-photon exchange in Fig. 5. Moreover, considering the fact that diagrams with one transverse photon across n-bubbles are suppressed by a factor \((\sqrt{|{\mathbf {p}}|})^n\), the numerable inifnity of contributions on the r.h.s. of Fig. 5 can be reduced to a finite set. The amplitudes corresponding to these diagrams can be evaluated via dimensional regularization as the ones containing radiation pions in Refs. [14, 24, 129] or via the cutoff approach and, in finite volume, they can be constructed by replacing the relevant integrals with three-dimensional sums, eventually regularized by a spherical cutoff.
Furthermore, the finite-volume quantization conditions can be derived as in Sect. 3.1, keeping track of the transverse-photon contributions via the aforementioned redefinition of the strong coupling constant. In the end of the process, an expression for \(1/D(E^*)\) analogous to Eq. (145) is found, provided the powers of the original strong coupling constant in the QED contributions to \(D_{\mathrm {T}}(E^*)\) in Fig. 5 are replaced by scattering parameters (cf. sec. III B of Ref. [94]) using the expression of \(D(E*)\) in Eq. (25).
In the present first-order approximation in the fine-structure constant, the latter operation is, in fact, justified. Dressing the S-wave strong interaction through the diagrams with one transverse-photon exchange between the legs of the strong vertex and the interaction-to-bubble exchange in fig. 4 (c) of Ref. [94], the low-energy constant \(C(E^*)\) picks up the \({\mathcal {O}}(\alpha )\) corrections shown in Eq. (25), which lead to the appearance of a term proportional to the square of the Lüscher function \({\mathcal {S}}(x)\) (cf. Eq. (28) of Ref. [94]) in the expression of the finite-volume ERE in Eq. (26) of Ref. [94]. By means of a procedure analogous to the one outlined in Sect. 3.3.2, it can be demonstrated that transverse-photon contributions materialise in the last term within the second curly brackets on the r.h.s. of Eqs. (36), (37) and (39) of Ref. [94]. Albeit pertinent, this contribution constitutes a subleading order correction to the term proportional to \({\mathcal {J}}\) within the same parentheses of the latter equations and is comparable in magnitude with the terms proportional to \((a_{{\mathrm {C}}}^{(1)}/\pi L)^2\) in Eq. (39) of Ref. [94].
Upon repetition of the ’dressing’ procedure in the P-wave case, we expect that the transverse-photon contributions make their appearance in Eqs. (218) and (219) only within the curly brackets opened by \(\xi \alpha a_{\mathrm {C}}^{(1)}/L^2\pi ^2\) and \(\xi \alpha {a'_{\mathrm {C}}}^{(1)}/L^2\pi ^2\) respectively, in the form of terms of order \(\xi \) or higher. Therefore our expressions of the lowest \(T_1\) unbound energy eigenvalue in Eq. (218) and of the corresponding finite-volume correction in Eq. (219) are incomplete at the considered order in 1/L and the scattering parameters, albeit exact in presence of the Coulomb photons alone. However, transverse photon contributions may have no effect in the final expression for the corrected version of \(\varDelta E_{B}^{(1,T_1)}\) in Eq. (232), due to the approximations performed in the derivation of the latter in Sect. 3.3.2.
As we previously noted, the second main generalization of our work consists of the adoption of strong interactions coupled to more units of angular momentum. The most significant of these extensions is represented by the D-wave case, where the strong part of the EFT Lagrangian density becomes
where \(F(E^*)\) is a new suitable energy-dependent coupling constant (cf. Sect. 2). Due to the presence of higher-order differential operators acting on the fermionic fields, the computation of the strong scattering amplitude, \(T_{\mathrm {S}}\), via a geometric series on the loop integrals, as in Eq. (15), involves a rank-four tensor as a ratio. The elements of the D-wave counterpart of \({\mathbb {J}}_0\) correspond to double mixed derivatives of the free Green’s function, except for the diagonal terms, in which an additional contribution proportional to \(G_0({\mathbf {0}},{\mathbf {0}})\) is expected to be present. Also the full Green’s function \(G_{\mathrm {SC}}({\mathbf {0}},{\mathbf {0}})\) is likely to undergo similar changes, which lead to the onset of more rapidly UV-divergent integrals in the D-wave counterpart of \({\mathbb {J}}_{\mathrm {SC}}\). Besides, some novelties are expected to arise from the quantization condition stemming from the full two-point correlation function \(G_{\mathrm {SC}}\). The D-wave counterpart of \({\mathbb {J}}_{\mathrm {C}}\) in finite volume generates the constraints on \(1/F^L(E^*)\) for energy states transforming as two distinct representations of the cubic group, \({\mathcal {O}}\). The \(\ell =2\) irreducible representation of \(\mathrm {SO}(3)\), in fact, decomposes into the \(E \oplus T_2\) irreps [60, 130] of \({\mathcal {O}}\). As a consequence, the one-to-one correspondence between the transformation properties of the selected multiplet of states under the operations of \(\mathrm {SO}(3)\) and \({\mathcal {O}}\) is no longer valid. It is, thus, possible that a derivation of the finite-volume corrections that makes use of the effective range expansion for D-waves in Ref. [37],
has to follow two separate paths for the E and the \(T_2\) states. New challenges arise also in the evaluation of the cutoff-regularized double sums stemming from the \(\delta {\tilde{p}}^2\) expansions (cf. Sect. 3.3.1) of the Lüscher functions. Nevertheless, the reference finite-volume state for the lowest unbound energy level is expected to correspond again to the one with \(|\tilde{{\mathbf {p}}}| = 1\) and energy \(4\pi ^2/L^2 M\). Therefore, the final formulae for the finite-volume energy corrections to the lowest E and \(T_2\) scattering states are likely to conserve some resemblance with the one presented in Eq. (219). Concerning the lowest bound state, it would be certainly of interest to compare the magnitude of the outcoming corrections with the existing ones for the energy of the most bound S- and P-wave states.
5 Conclusion
In this paper, we have extended the investigation of QED for low-energy scattering to the case of spinless fermions strongly coupled to one unit of angular momentum in the framework of pionless EFT. Among the forces of electromagnetic nature, the electrostatic interaction represents the dominant contribution to T-matrix elements in the low-energy sector and the Coulomb ladders have to be resummed to all orders in the fine-structure constant.
A pivotal role in the procedure has been covered by the non-perturbative formalism based on the full Coulomb propagator developed comprehensively in Ref. [27] in the context of pp scattering. Differently from the transverse photons, the Coulomb ones do not propagate between the fermionic bubbles in the diagrams, a crucial feature that permits to rewrite the full two-body Green function operator in terms of the Coulomb one and operator representing the P-wave strong interaction. It is exactly the same property that led us to write the T-matrix element of the scattering processes and the full Green’s function in closed form, thus paving the way to the derivation of the quantization conditions. Moreover, though the analysis of the attractive Coulomb case, the observations on the scattering parameters pointed out in sec. 3.4 of Ref. [27] have found here another confirmation.
Second, the infinite-volume analysis of fermion-fermion scattering in Sects. 2–2.3 allowed us to attain our main goal, the derivation of finite-volume energy corrections for two-body P-wave bound and scattering states, by providing an extension of the analysis on S-wave states in Ref. [94]. Motivated by the growing interest for lattice EFTs and, above all, LQCD, we have transposed our system of charged particles in a cubic box with periodic boudary conditions.
Having regards to the prescriptions from the literature [93, 106], we have removed the zero momentum modes from the relevant three-dimensional sums and considered the QED corrections to the mass of the spinless particles [40, 48], in sight of the application of our results to realistic baryon–baryon systems on the lattice [65]. Furthermore, the characteristic size of our cubic box has been chosen to fulfill the constraint \(ML \ll 1/\alpha \), which is required for the viability of the perturbative approach of QED in the cubic finite-volume. Under this hypothesis, the non-relativistic relation between the finite-volume energy of two composite fermions in the \(T_1\) representation of the cubic group and its P-wave scattering parameters receives QED corrections obtainable in closed form.
Although more cumbersome than the S-wave counterpart, the expression we have presented in secs. 3.3.1 for the energy shift of the lowest unbound state resembles the features of the one in sec. III D 1 of Ref. [94], except for the appearance of higher-order scattering parameters. Besides, the finite-volume corrections for the P-wave bound state prove to have the opposite sign and the same magnitude of the ones for the S-wave state in sec. III D 3 of Ref. [94], up to contributions of order \(1/L^3\). This fact confirms the long-standing observations on the \(A_1\) and \(T_1\) finite-volume energy eigenvalues in the analysis of Refs. [66, 72], drawn in the context of a two-body system governed by finite-range interactions in the non-relativistic regime.
In the latter work, the interplay of parity and angular momentum quantum numbers in the wavefunctions was found to be responsible of the relation between the leading-order S- and P-wave energy shifts. Only the generalization of our analysis will tell if the existing relationships between the finite-volume shifts in tab. I of Ref. [66] for two-body states with higher angular momentum remain at least approximately valid in presence of QED.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: This is a purely theoretical work and thus contains no data.]
Notes
Throughout, we use the abbreviation “irrep” for an irreducible representation.
Finite volume physical quantities will be denoted henceforth with an L in the superscript.
References
J. Bijnens, U.-G. Meißner, Workshop on the standard model at low-energies: Miniproceedings (International Workshop on the Standard Model at Low Energies, ECT, Trento, 1996). arXiv:hep-ph/9606301
U. van Kolck, Nucl. Phys. A 645(2), 273–302 (1999)
E. Epelbaum, Progr. Part. Nucl. Phys. 57(2), 654–741 (2006)
D. Lee, Progr. Part. Nucl. Phys. 63, 117–154 (2009)
E. Epelbaum, H.W. Hammer, U.-G. Meißner, Rev. Mod. Phys. 81, 1773–1825 (2009). https://doi.org/10.1103/RevModPhys.81.1773
R. Machleidt, D. Entem, Phys. Rep. 503(1), 1–75 (2011)
T.A. Lähde, U.-G. Meißner, Nuclear Lattice Effective Field Theory, Lecture Notes in Physics 957. Springer, New York (2019). https://doi.org/10.1007/978-3-030-14189-9
H.W. Hammer, S. König, U. van Kolck, Rev. Mod. Phys. 92(025004), 2 (2020). https://doi.org/10.1103/RevModPhys.92.025004
D.B. Kaplan, M.J. Savage, M.B. Wise, Nucl. Phys. B 478, 629–659 (1996)
D.B. Kaplan, M.J. Savage, M.B. Wise, Phys. Lett. B 424, 390–396 (1998)
P.F. Bedaque, U. van Kolck, Phys. Lett. B 428, 221–226 (1998)
P.F. Bedaque, H.-W. Hammer, U. van Kolck, Phys. Rev. Lett. 82, 463 (1999). https://doi.org/10.1103/PhysRevLett.82.463
J. Gegelia, Phys. Lett. B 429(3–4), 227–231 (1998)
D.B. Kaplan, M.J. Savage, M.B. Wise, Nucl. Phys. B 534, 329–355 (1998)
D.B. Kaplan, Nucl. Phys. B 494, 471–483 (1997)
J.-W. Chen, G. Rupak, M.J. Savage, Nucl. Phys. A 653(4), 386–412 (1999)
P.F. Bedaque, H.-W. Hammer, U. van Kolck, Nucl. Phys. A 646(4), 444–466 (1999)
P.F. Bedaque, H.-W. Hammer, U. van Kolck, Nucl. Phys. A 676(1–4), 357–370 (2000)
I.R. Afnan, D.R. Phillips, Phys. Rev. C 69, 034010 (2003). https://doi.org/10.1103/PhysRevC.69.034010
H.W. Grießhammer, Nucl. Phys. A 744, 192–226 (2004)
F. Gabbani, P.F. Bedaque, H.W. Grießhammer, Nucl. Phys. A 675(3–4), 601–620 (2000)
B. Blankkreider, J. Gegelia, AIP Conf. Proc. 603, 233 (2001). https://doi.org/10.1063/1.1436604
P.F. Bedaque, G. Rupack, H.W. Grießhammer, H.-W. Hammer, Nucl. Phys. A 714(3–4), 589–610 (2003)
D.B. Kaplan, M.J. Savage, M.B. Wise, Phys. Rev. C 59, 617 (1999). https://doi.org/10.1103/PhysRevC.59.617
J.-W. Chen, H.W. Grießhammer, M.J. Savage, R.P. Springer, Nucl. Phys. A 644(3), 221–234 (1998)
M.J. Savage, K.A. Scaldeferri, M.B. Wise, Nucl. Phys. A 652(3), 273–286 (1999)
X. Kong, F. Ravndal, Nucl. Phys. A 665, 137–163 (2000)
X. Kong, F. Ravndal, Phys. Lett. B 470(1–4), 1–5 (1999)
X. Kong, F. Ravndal, Phys. Rev. C 64, 044002 (2001). https://doi.org/10.1103/PhysRevC.64.044002
C.A. Bertulani, H.-W. Hammer, U. van Kolck, Nucl. Phys. A 712, 37–58 (2002)
J. Gasser, V.E. Lyubovitskij, A. Rusetski, Phys. Rep. 456(5–6), 167–251 (2008)
R.J. Furnstahl, Lecture notes of the course of Nuclear Few- and Many-Body Physics, Nuclear Forces 2, Ohio State University (2014)
M.D. Barker, P.C. Colby, P. Signell, Phys. Rev. Lett. 48, 918 (1982). https://doi.org/10.1103/PhysRevLett.48.918
L.D. Landau, J. Smorodinski, J. Phys. Acad. Sci. USSR 8, 219 (1944)
L.D. Landau, J. Smorodinski, J. Phys. Acad. Sci. USSR 11, 195 (1947)
H.A. Bethe, Phys. Rev. 76, 38 (1949). https://doi.org/10.1103/PhysRev.76.38
L.P. Kok, J.W. de Maag, H.H. Bouwer, H. van Haeringen, Phys. Rev. C 26, 2381–2396 (1982). https://doi.org/10.1103/PhysRevC.26.2381
E. Klempt, F. Bradamante, A. Martin, J.-M. Richard, Phys. Rep. 368, 119–316 (2002)
J. Carbonell, O.D. Dalkarov, K.V. Protasov, I.S. Shapiro, Nucl. Phys. A 535, 651–668 (1991)
Z. Davoudi, M.J. Savage, Phys. Rev. D 90, 054503 (2014). https://doi.org/10.1103/PhysRevD.90.054503
Z. Davoudi, J. Harrison, A. Jüttner, A. Portelli, M.J. Savage, Phys. Rev. D 99, 034510 (2019). https://doi.org/10.1103/PhysRevD.99.034510
S. Dürr, Z. Fodor, J. Frison, C. Hoelbling, R. Hoffmann, S.D. Katz, S. Krieg, T. Kurth, L. Lellouch, T. Lippert, K.K. Szabo, G. Vulvert, Science 322(5905), 1224–1227 (2008)
S. Aoki, K.-I. Ishikawa, N. Ishizuka, K. Kanaya, Y. Kuramashi, Y. Nakamura, Y. Namekawa, M. Okawa, Y. Taniguchi, A. Ukawa, N. Ukita, T. Yoshié, Phys. Rev. D 86, 034507 (2012). https://doi.org/10.1103/PhysRevD.86.034507
S. Dürr, Z. Fodor, C. Hoelbling, S. Krieg, T. Kurth, L. Lellouch, T. Lippert, R. Malak, T. Métivet, A. Portelli, A. Sastre, K.K. Szabó, Phys. Rev. C 90, 114504 (2014). https://doi.org/10.1103/PhysRevD.90.114504
S. Aoki, Y. Aoki, D. Bečirević, C. Bernard, T. Blum, G. Colangelo, M. Della Morte, P. Dimopoulos, S. Dürr, H. Fukaya, M. Golterman, Steven Gottlieb, S. Hashimoto, U. M. Heller, R. Horsley, A. Jüttner, T. Kaneko, L. Lellouch, H. Leutwyler, C.-J. D. Lin, V. Lubicz, E. Lunghi, R. Mawhinney, T. Onogi, C. Pena, C. T. Sachrajda, S. R. Sharpe, S. Simula, R. Sommer, A. Vladikas, U. Wenger and H. Wittig, Eur. Phys. J. C 77, 112 (2017)
B.C. Toth, Proc. of Sc. 363, XXXVII International Symposioum on Lattice Field Theory, Wuhan, China (2019)
S. Aoki, Y. Aoki, D. Becirevic, T. Blum, G. Colangelo, S. Collins, M. Della Morte, P. Dimopoulos, S. Dürr, H. Fukaya, M. Golterman, Steven Gottlieb, R. Gupta, S. Hashimoto, U. M. Heller, G. Herdoiza, R. Horsley, A. Jüttner, T. Kaneko, C.-J. D. Lin, E. Lunghi, R. Mawhinney, A. Nicholson, T. Onogi, C. Pena, A. Portelli, A. Ramos, S. R. Sharpe, J. N. Simone, S. Simula, R. Sommer, R. Van De Water, A. Vladikas, U. Wenger, H. Wittig, Eur. Phys. J. C 80, 113 (2020)
S. Uno, M. Hayakawa, Progr. Theor. Phys. 120(3), 413–441 (2008)
A. Portelli, S. Dürr, Z. Fodor, J. Frison, C. Hoelbling, S. D. Katz, S. Krieg, T. Kurth, L. Lellouch, T. Lippert, A. Ramos and K. K. Szabó, Proc. of Sc. 139, XXIX International Symposium on Lattice Field Theory, Squaw Valley, Lake Tahoe, California (2011)
G.M. de Divitiis, R. Frezzotti, V. Lubicz, G. Martinelli, R. Petronzio, G.C. Rossi, F. Sanfilippo, S. Simula, N. Tantalo, Phys. Rev. C 87, 114505 (2013). https://doi.org/10.1103/PhysRevD.87.114505
S. Borsanyi, S. Dürr, Z. Fodor, J. Frison, C. Hoelbling, S.D. Katz, S. Krieg, T. Kurth, L. Lellouch, T. Lippert, A. Portelli, A. Ramos, A. Sastre, K. Szabo, Phys. Rev. Lett. 111, 252001 (2013). https://doi.org/10.1103/PhysRevLett.111.252001
S. Drury, T. Blum, M. Hayakawa, T. Izubuchi, C. Sachrajda and R. Zhou, Proc. of Sc. 187, XXXI International Symposioum on Lattice Field Theory, Mainz, Germany (2013)
S. Borsanyi, S. Durr, Z. Fodor, C. Hoelbling, S.D. Katz, S. Krieg, L. Lellouch, T. Lippert, A. Portelli, K.K. Szabo, B.C. Toth, Science 347(6229), 1452–1455 (2015)
R. Horsley, Y. Nakamura, H. Perlt, D. Pleiter, P.E.L. Rakow, G. Schierholz, A. Schiller, R. Stokes, H. Stüben, R.D. Young, J.M. Zanotti, J. High Energy Phys. 2016, 93 (2016). https://doi.org/10.1007/JHEP04(2016)093
R. Horsley, Y. Nakamura, H. Perlt, D. Pleiter, P.E.L. Rakow, G. Schierholz, A. Schiller, R. Stokes, H. Stüben, R.D. Young, J. Phys. G 43, 10 (2016). https://doi.org/10.1088/0954-3899/43/10/10LT02
R. Horsley, Z. Koumi, Y. Nakamura, H. Perlt, D. Pleiter, P.E.L. Rakow, G. Schierholz, A. Schiller, H. Stüben, R.D. Young, J. Phys. G 46, 11 (2019). https://doi.org/10.1088/1361-6471/ab32c1
Z.R. Kordov, R. Horsley, Y. Nakamura, H. Perlt, P.E.L. Rakow, G. Schierholz, H. Stüben, R.D. Young, J.M. Zanotti, Phys. Rev. D 101, 034517 (2020). https://doi.org/10.1103/PhysRevD.101.034517
T. Métivet, Lattice QCD at the physical point : pion-pion scattering and structure of the nucleon, Ph.D. Dissertation, CEA Saclay (2015)
N.R. Acharya, F.-K. Guo, U.-G. Meißner, C.Y. Seng, Nucl. Phys. B 922, 480–498 (2017)
R.C. Johnson, Phys. Lett. B 114, 147–151 (1982)
B.N. Lu, T.A. Lähde, D. Lee, U.-G. Meißner, Phys. Rev. D 90, 034507 (2014). https://doi.org/10.1103/PhysRevD.90.034507
B.N. Lu, T. Lähde, D. Lee, U.G. Meißner, Phys. Rev. D 92, 014506 (2015). https://doi.org/10.1103/PhysRevD.92.014506
G. Stellin, S. Elhatisari, U-.G. Meißner, Eur. Phys. J. 54, 232 (2018). https://doi.org/10.1140/epja/i2018-12671-6
D. Lee, R. Thomson, Phys. Rev. C 75, 064003 (2007). https://doi.org/10.1103/PhysRevC.75.064003
S. R. Beane, W. Detmold, R. Horsley, M. Illa, M. Jafry, D. J. Murphy, Y. Nakamura, H. Perlt, P. E. L. Rakow, G. Schierholz, P. E. Shanahan, H. Stüben, M. L. Wagman, F. Winter, R. D. Young and J. M. Zanotti, Charged multi-hadron systems in lattice QCD+QED. arXiv:2003.12130v2 [hep-lat] (2020)
S. König, D. Lee, H.-W. Hammer, Ann. Phys. 327, 1450 (2012)
J.-Y. Pang, J.-J. Wu, H.-W. Hammer, U.-G. Meißner, A. Rusetsky, Phys. Rev. D 99, 074513 (2019). https://doi.org/10.1103/PhysRevD.99.074513
K. Huang, C.N. Yang, Phys. Rev. 105(3), 767 (1957). https://doi.org/10.1103/PhysRev.105.767
M. Lüscher, Commun. Math. Phys. 104, 177 (1986)
M. Lüscher, Commun. Math. Phys. 105, 153 (1986)
M. Lüscher, Nucl. Phys. B 354, 531–578 (1991)
S. König, D. Lee, H.-W. Hammer, Phys. Rev. Lett. 107, 112001 (2011). https://doi.org/10.1103/PhysRevLett.107.112001
T.C. Luu, M.J. Savage, Phys. Rev. D 83, 114508 (2011). https://doi.org/10.1103/PhysRevD.83.114508
M. Döring, U.G. Meißner, E. Oset, A. Rusetsky, Eur. Phys. J. A 48, 114 (2012). https://doi.org/10.1140/epja/i2012-12114-6
K. Rummukainen, S.A. Gottlieb, Nucl. Phys. B 450, 397 (1995)
C.H. Kim, C.T. Sachrajda, S.R. Sharpe, Nucl. Phys. B 727, 218 (2005)
Z. Davoudi, M.J. Savage, Phys. Rev. D 84, 114502 (2011). https://doi.org/10.1103/PhysRevD.84.114502
S. Bour, S. König, D. Lee, H.-W. Hammer, U.-G. Meißner, Phys. Rev. D 84, 091503 (2011). https://doi.org/10.1103/PhysRevD.84.091503
M. Göckeler, R. Horsley, M. Lage, U.-G. Meißner, P.E.L. Rakow, A. Rusetsky, G. Schierholz, J.M. Zanotti, Phys. Rev. D 86, 094513 (2012). https://doi.org/10.1103/PhysRevD.86.094513
A. Rokash, E. Epelbaum, H. Krebs, D. Lee, U.-G. Meißner, J. Phys. G 41, 015105 (2014). https://doi.org/10.1088/0954-3899/41/1/015105
C.T. Sachrajda, G. Villadoro, Phys. Lett. B 609, 73 (2005)
M. Döring, U.G. Meißner, E. Oset, A. Rusetsky, Eur. Phys. J. A 47, 139 (2011). https://doi.org/10.1140/epja/i2011-11139-7
R.A. Briceno, Z. Davoudi, T.C. Luu, M.J. Savage, Phys. Rev. D 89, 074509 (2014). https://doi.org/10.1103/PhysRevD.89.074509
C. Körber, T.C. Luu, Phys. Rev. C 93, 054002 (2016). https://doi.org/10.1103/PhysRevC.93.054002
B. Scheuetrumpf, W. Nazarewicz, P.-G. Reinhard, Phys. Rev. C 93, 054304 (2016). https://doi.org/10.1103/PhysRevC.93.054304
A. Cherman, S. Sen, M.L. Wagman, L.G. Yaffe, Phys. Rev. D 95, 074512 (2017). https://doi.org/10.1103/PhysRevD.95.074512
V. Bernard, M. Lage, U.G. Meißner, A. Rusetsky, J. High Energy Phys. 08, 024 (2008). https://doi.org/10.1088/1126-6708/2008/08/024
R.A. Briceño, M.T. Hansen, Phys. Rev. D 92, 074509 (2015). https://doi.org/10.1103/PhysRevD.92.074509
K. Polejaeva, A. Rusetsky, Eur. Phys. J. A 48, 67 (2012). https://doi.org/10.1140/epja/i2012-12067-8
U.-G. Meißner, G. Rios, A. Rusetsky, Phys. Rev. Lett. 114, 091602 (2015). https://doi.org/10.1103/PhysRevLett.114.091602
S. König, D. Lee, Phys. Lett. B 779, 9–15 (2018)
R.A. Briceño, J.J. Dudek, R.D. Young, Rev. Mod. Phys. 90(025001), 2 (2018). https://doi.org/10.1103/RevModPhys.90.025001
A. Duncan, E. Eichten, H. Thacker, Phys. Rev. Lett. 76, 3894 (1996). https://doi.org/10.1103/PhysRevLett.76.3894
S.R. Beane, M.J. Savage, Phys. Rev. D 90, 074511 (2014). https://doi.org/10.1103/PhysRevD.90.074511
C. Deng, H. Chen, J. Ping, Phys. Rev. D 101, 054039 (2020). https://doi.org/10.1103/PhysRevD.101.054039
V. Komarov, D. Tsirkov, T. Azaryan, Z. Bagdasarian, S. Dymov, R. Gebel, B. Gou, A. Kacharava, A. Khoukaz, A. Kulikov, V. Kurbatov, B. Lorentz, G. Macharashvili, D. Mchedlishvili, S. Merzliakov, S. Mikirtytchiants, H. Ohm, M. Papenbrock, F. Rathmann, V. Serdyuk, V. Shmakova, H. Ströher, S. Trusov, Y. Uzikov, Y. Valdau, Phys. Rev. C 93, 6, 065206 (2016). https://doi.org/10.1103/PhysRevC.93.065206
Y.X. Liu, J.S. Li, C.G. Bao, Phys. Rev. C 67, 055207 (2003). https://doi.org/10.1103/PhysRevC.67.055207
H. Clement, Progr. Part. Nucl. Phys. 93, 195–242 (2017)
F.-K. Guo, C. Hanhart, U.-G. Meißner, Q. Wang, Q. Zhao, B.-S. Zou, Rev. Mod. Phys. 90, 015004 (2008). https://doi.org/10.1103/RevModPhys.90.015004
U.-G. Meißner, J.A. Oller, Phys. Lett. B 751, 59 (2015)
Y. Yamaguchi, E. Santopinto, Phys. Rev. D 96(1), 014018 (2017). https://doi.org/10.1103/PhysRevD.96.014018
J. He, Phys. Rev. D 95, 074004 (2017). https://doi.org/10.1103/PhysRevD.95.074004
Y. Shimizu, Y. Yamaguchi, M. Harada, Progr. Theor. Exp. Phys. 2019, 12 (2019)
W.E. Caswell, G.P. Lepage, Phys. Lett. B 167, 437–442 (1986)
T. Kinoshita, M. Nio, Phys. Rev. D 53, 4909–4929 (1996). https://doi.org/10.1103/PhysRevD.53.4909
E. Hilf, L. Polley, Phys. Lett. B 131(4–6), 412 (1983)
P.F. Bedaque, U. van Kolck, Ann. Rev. Nucl. Part. Sci. 52, 339 (2002). https://doi.org/10.1146/annurev.nucl.52.050102.090637
H.-W. Hammer, L. Platter, Ann. Rev. Nucl. Part. Sci. 60, 207 (2010). https://doi.org/10.1146/annurev.nucl.012809.104439
H.W. Grießhammer, J.A. McGovern, D.R. Phillips, G. Feldman, Progr. Part. Nucl. Phys. 67(4), 841 (2012)
S. König, H.W. Grießhammer, H.-W. Hammer, U. van Kolck, J. Phys. G Nucl. Part. Phys. 43, 5 (2016). https://doi.org/10.1088/0954-3899/43/5/055106
A. Agadjanov, Hadronic Electroweak Processes in a Finite Volume, Ph.D. Thesis, Univ. Bonn (2017)
P.F. Bedaque, H.-W. Hammer, U. van Kolck, Phys. Lett. B 569, 159–167 (2003)
P. Ramond, Field Theory: A Modern Primer, 2nd edn. (Westview Press, Boulder, 1997)
R. Omnès, Introduction to Particle Physics (Wiley, Amsterdam, 1970)
A.L. Fetter, J.D. Walecka,Quantum Theory of Many-Particle Systems, pp. 21–31, Dover (2003)
H.A. Bethe, E.E. Salpeter, Quantum Mechanics of One- and Two-Electron Systems, S. Flügge, Encyclopedia of Physics, Atome I, XXXV, pp. 88–436, Springer, Berlin (1957)
M.H. Hull, G. Breit, Coulomb Wave Functions in S. Flügge, Encyclopedia of Physics, Nuclear Reactions II: Theory, XLI/1, pp. 408–465, Springer, Berlin (1959). https://doi.org/10.1007/978-3-642-45923-8_2
D.R. Harrington, Phys. Rev. 139(3B), 691–695 (1965). https://doi.org/10.1103/PhysRev.139.B691
M.L. Goldberger, K.M. Watson, Collision Theory (Dover, Illionis, 1964)
F.L. Yost, J.A. Wheeler, G. Breit, Phys. Rev. 49, 174–189 (1936). https://doi.org/10.1103/PhysRev.49.174
J.C. Collins, Renormalization, Cambridge Monographs on Mathematical Physics (Cambridge University Press, Cambridge, 1984)
E. Epelbaum, U.-G. Meißner, Phys. Lett. B 461(3), 287–294 (1999)
W. Greiner, J.A. Maruhn, Nuclear Models (Springer, New York, 1996). https://doi.org/10.1007/978-3-642-60970-1
L.R. Carter, Molecular Symmetry and Group Theory (Wiley, Amsterdam, 1997)
S.R. Beane, E. Chang, W. Detmold, H.W. Lin, T.C. Luu, K. Orginos, A. Parreño, M.J. Savage, A. Torok, A. Walker-Loud, Phys. Rev. D 85, 054511 (2012). https://doi.org/10.1103/PhysRevD.85.054511
T. Yamazaki, K.-I. Ishikawa, Y. Kuramashi, A. Ukawa, Phys. Rev. D 86, 074514 (2012). https://doi.org/10.1103/PhysRevD.86.074514
S.R. Beane, E. Chang, S. Cohen, W. Detmold, H. Lin, T.C. Luu, K. Orginos, A. Parreño, M.J. Savage, A. Walker-Loud, Phys. Rev. D 87, 034506 (2013). https://doi.org/10.1103/PhysRevD.87.034506
S.R. Beane, E. Chang, S.D. Cohen, W. Detmold, P. Junnarkar, H.W. Lin, T.C. Luu, K. Orginos, A. Parreño, M.J. Savage, A. Walker-Loud, Phys. Rev. C 88, 024003 (2013). https://doi.org/10.1103/PhysRevC.88.024003
T. Mehen, I.W. Stewart, Nucl. Phys. A 665, 164 (2000)
S. Altmann, Math. Proc. Phyl. Soc. 53(2), 343–367 (1957)
C. Cohen-Tannoudji, B. Diu, F. Laloë, Quantum Mechanics, Vol. 1, 1st Edition, Wiley, Amsterdam (1977)
M. E. Rose, Elementary Theory of Angular Momentum, 1st Edition, Struct. of Matter Series, John Wiley and Sons (1957); 2nd Edition, Dover (1995)
G.B. Arfken, H.J. Weber, F.E. Harris, Mathematical Methods for Physicists, 7th edn. (Academic Press, New York, 2012)
C. Cohen-Tannoudji, B. Diu, F. Laloë, Quantum Mechanics, Vol. 2, 1st Edition, Wiley, Amsterdam (1977)
S. Tan, Phys. Rev. A 78, 013636 (2008). https://doi.org/10.1103/PhysRevA.78.013636
Acknowledgements
First of all, we express our gratitude to Akaki Rusetski, Andria Agadjanov and Wael Elkamhawy for the precious advice and their expertise in effective field theories and Filippo Stellin for the useful suggestions in the drafting of the manuscript. Secondly, we thank Serdar Elhatisari for his introduction to cuda C++ programming for the GPUs, a crucial tool for the precise evaluation of the double sums. Then, we recognize the contributions by Timo A. Lähde, Andreas Nogga, Paul Kapinos and Dieter an Mey in the technical assistance. We also thank Hans-Werner Hammer for a useful communication. Besides, we acknowledge financial support from the Deutsche Forschungsgemeinschaft (Sino-German CRC 110, Grant No. TRR 110) and the VolkswagenStiftung (Grant No. 93562). The work of UGM was also supported by the Chinese Academy of Sciences (CAS) President’s International Fellowship Initiative (PIFI) (Grant No. 2018DM0034). Finally, we acknowlegde computational resources provided by RWTH Aachen (JARA 0015 project).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Vittorio Somá
Appendices
Appendix
Feynman rules
For the computation of the amplitude associated to each Feynman diagram in the framework of a non-relativistic effective field theory for spinless fermions with NRQED corrections, the rules in Fig. 6 are understood. The imaginary part in the denominator of the retarded fermion propagators \(\epsilon \) and the photon mass \(\lambda \) are arbitrarily small quantities.
Integrals in dimensional regularization
In this section the evaluation of the second term on the r.h.s. of Eq. (30) for \(T_{\mathrm {SC}}^{\mathrm {tree}}({\mathbf {p}},{\mathbf {p}}')\) is explicitly shown, that is the derivation of the new contribution to Eq. (31). In d dimensions, the last integral in Eq. (30) becomes
Since the loop integral is not going to be performed in the complex plane, the parameter \(\epsilon \) can be set to zero. Applying the Feynman parametrization for the denominators, we obtain
Then, we rewrite the polynomial in the denominator as \({\mathbf {l}}^2 - 2{\mathbf {p}}\cdot {\mathbf {l}}(1-\omega ) + \omega \lambda ^2\) and consider the application of the dimensional regularization formula in Eq. (B.17) in Ref. [113] for the carrying-out of the momentum integral,
As the r.h.s. of the last equation is non-singular in three dimensions, the limit \(d \rightarrow 3\) can be safely taken. Furthermore, we define the auxiliary quantities
Performing the change of variables \(\omega \mapsto \omega '\equiv (\omega -\beta )/\gamma \) in the integrand of Eq. (237), we obtain
The last expression can be integrated,
After evaluating the results of the integration over \(\omega '\) in terms of the original variables, \({\mathbf {p}}\) and \(\lambda \), a closed form for \({\mathfrak {K}}\) is found,
where the conventions \(\log (-\mathrm {i}) = -\mathrm {i}\pi /2\) and \(\sqrt{-1} = -\mathrm {i}\) are understood. Plugging Eq. (241) into Eq. (237), the desired result is obtained,
In the second part of this appendix, we evaluate the momentum integrals appearing in the 1-loop diagram with one Coulomb photon exchange inside the loop (cf. right part of the Fig. 2 and Eq. (34)). To this aim, we first introduce the notation \(\gamma ^2 \equiv -{\mathbf {p}}^2\) for the physical momenta, we set \(\varepsilon \) to zero and rewrite Eq. (33) in arbitrary dimensions d as
where the fictitious photon mass has been set to zero, since no infrared divergences occur in the integration (cf. Appendix A of Ref. [27]). Secondly, we decide to carry out the integration over \({\mathbf {k}}\) first and merge the relevant denominators again by means of Feynman’s trick, obtaining
where \(\varDelta ^2 \equiv \gamma ^2 + {\mathbf {q}}^2(1-\omega )\) and Einstein’s convention for repeated indices is understood. Now, we can proceed by evaluating the two integrals over \({\mathbf {k}}\) generated by \(q_ik_j\) and \(k_ik_j\) separately. The former integral turns out to be an application of Eq. (B.18) in Ref. [113] and gives
The second term of Eq. (244), instead, yields two contributions, one of the two being proportional to the r.h.s. of Eq. (245). The application of Eq. (B.18) in Ref. [113] indeed leads to
By comparison of the last equation with Eq. (244), we observe that the \({\mathbf {q}}\) integrals involving \(q_i q_j\) can be performed together. Therefore, we group the two terms together with the necessary constants and, after few manipulations, we define
Then, with the help of the auxiliary parameter \(\varXi _4^2 \equiv \gamma ^2/[\omega (1-\omega )]\) we apply again the Feynman parametrization for the two denominators and rewrite the last equation as
In this form, the application of Eq. (B.18) in Ref. [113] with \({\mathbf {q}}=0\) suffices for the carrying out of the momentum integral in \({\mathfrak {L}}_1\),

and Eq. (248) becomes
where the Gamma functions have been simplified. While the integration over \(\phi \) is straightforward and gives 2/d, the remaining one can be performed in an analogous fashion as Eq. (A.6) of Ref. [27]. By considering \(\epsilon \equiv 3-d\), in fact, the integrand can be expanded in a power series in \(\epsilon \), giving
Introducing also the renormalization scale \(\mu \), the part of the scattering amplitude of interest can be recast as
It displays a pole singularity in the limit \(d\rightarrow 3\) and a simple PDS pole at \(d=2\). By exploiting the Laurent series expansion of the Gamma function for small arguments and truncating it at NLO, \({\mathfrak {L}}_1\) finally becomes
where the regular parts of the amplitude have been evaluated in the three-dimensional limit. Now, due to the presence of a \(d=2\) singularity, the PDS correction to \({\mathfrak {L}}_1\) is non-zero. Introducing again the renormalization scale \(\mu \) of the MS scheme and noticing that the integrand in Eq. (252) in the \(d\rightarrow 2\) limit coincides with 1, the correction turns out to be
Subtracting the latter equation to Eq. (253), the PDS corrected part of the amplitude can be obtained,
Next, we concentrate on the evaluation of the second term on the second row of Eq. (244). Considering the original constant factors and the integral over the \({\mathbf {q}}\), we define
and the constant \(\varXi _5^2 \equiv \gamma ^2/[\omega (1-\omega )]\), so that we can exploit again the Feynman parametrization for the denominators, obtaining
The integral over the \({\mathbf {q}}\) can be now carried out as a straightforward application of Eq. (B.16) in Ref. [113], yielding

In the last rewriting, the integral over the \(\phi \) can be immediately performed, while the Gammas can again be simplified and reduced, so that Eq. (258) transforms into
where the conventional renormalization scale factor \((\mu /2)^{3-d}\) has been introduced as in Eq. (252). The remaining integral has been already met in Eq. (254) and it can be evaluated exactly in \(d=2\) or expanded in powers of \(3-d\) in the three-dimensional case. Plugging Eq. (251) into Eq. (258), it turns out that the integral is again divergent in the limit \(d\rightarrow 3\) and includes also a threefold PDS pole in \(d\rightarrow 2\). Taking the former limit, the Gamma function can be expanded in power series as before and the amplitude can be re-expressed as
where the ultraviolet divergence of the original integral is made explicit. Then, the application of the PDS scheme to the \(d\rightarrow 2\) pole yields the following correction,
Finally, we subtract the PDS contribution just determined to Eq. (260), obtaining
Now we collect the two results in Eqs. (255) and (262) and write the one-loop scattering amplitude with one photon exchange in the power divergence subtraction scheme,
Three dimensional integrations
Here, we focus our attention on the computation of the leading order matrix element of the Coulomb-corrected strong fermion-fermion scattering amplitude in Eq. (56). The process can be reduced to the evaluation of only one of the two integrals presented in the third row of the last equation, by virtue of the complex-conjugation property satisfied by the repulsive Coulomb wavefunctions, \(\psi _{{\mathbf {p}}'}^{(-)*} = \psi _{-{\mathbf {p}}'}^{(+)}\). In particular, we choose to concentrate on the first term on the l.h.s. of Eq. (56),
Recalling the parity rule of the spherical harmonics (cf. sec. \(A_{VI}\) in Ref. [134]), the repulsive Coulomb eigenstate turns out to be given by
Now, we start by observing that the three-dimensional Dirac delta function peaked at the origin can be rewritten in spherical coordinates as
due to rotational invariance. The last equation can be proven by exploiting the integral representation of \(\delta ({\mathbf {r}})\) [131], then expressing the exponential in terms of spherical harmonics and spherical Bessel functions of the first kind and finally performing the angular and radial integrations by means of the identity in sec. 11.2 of Ref. [133]. Besides, the rewriting in Eq. (266) paves the way for the integration of the angular variables and on the radial distance on which the Dirac delta effectively acts separately. Equipped with the last equation, we can split the expression in Eq. (264) into two parts,
where
and
Considering the explicit expression for the regular repulsive Coulomb eigenfunctions in Eq. (40), we first concentrate on the application of nabla to \(F_{\ell }(\eta ,|{\mathbf {p}}'|r')/|{\mathbf {p}}'|r'\). Recalling the transformation property of the Kummer functions, i.e. the confluent Hypergeometric functions \({}_1\mathrm {F}_1\), under differentiation with respect to their third argument
we can rewrite the term of interest as
In the last equation, we note that the application of the gradient effectively reduces to the application of the derivative with respect to the radial variable \(r'\), therefore the resulting vector is parallel to \({\mathbf {r}}'\). It is then convenient to exploit the expression of the latter vector in terms of the spherical harmonics given in Eq. (5.24) and sec. 5.1 of Ref. [123], in order to perform the integration on the radial and the angular variables associated to \(r'\) in Eq. (268) separately. Making use of the complex conjugation (cf. Eq. (4.31) in Ref. [132]) and the orthonormality (cf. chap. VI of Ref. [131]) properties of spherical harmonics, the integral over the angular variables can be carried out rapidly, obtaining
where \(\varOmega '\) denotes collectively the angular variables associated to \({\mathbf {r}}'\). Recalling Eq. (5.24) and sec. 5.1 in Ref. [123], the remaining spherical harmonic on the last row of Eq. (272) together with the round bracket with the Kronecker deltas can be identified as the unit-vector parallel to \({\mathbf {p}}'\), up to a multiplication factor that cancels out with \(2\sqrt{\pi /3}\) on the left of the last integration sign. Then, exploiting Eq. (271) for \(\ell =1\), Eq. (272) can be rewritten as
The explicit evaluation of the limit yields immediately to the disappearance of the terms depending linearly on the radial coordinate \(r'\), since the Kummer functions are equal to unity for zero values of the third argument,
Besides, by exploiting the fundamental property \(\varGamma (z+1)=z\varGamma (z)\) of the Gamma functions, the constants outside the limit in Eq. (273) can be rewritten in terms of the Sommerfeld factor (cf. Eq. (41)),
thus recovering the polynomial on the r.h.s of the generalized effective range expansion (cf. Eq. (51)). Equipped with the two last results we can, finally, obtain the desired expression for the r.h.s. of Eq. (272),
Now, we can proceed with the application of the gradient to the spherical harmonics (cf. Eq. (269)). From Ref. [123], the result of the latter derivative can be rewritten as a linear combination of shperical harmonics as in eqs. (5.24) and (5.27) in Ref. [123]. In particular, by the introduction of \(1=\sqrt{4\pi }Y_0^{0*}(\theta ,\varphi )\) in the relevant integral of Eq. (269), we can observe that the surface integrals over the \(Y_{\ell +1}^{\mu }(\theta ,\varphi )\) yield no contribution, since \(\ell \) cannot assume negative values. It follows that our term of interest becomes
where the Clebsch-Gordan coefficients \((j_1 j_2 J|m_1 m_2 M) \equiv \langle J M, j_1 j_2 | j_1 m_1, j_2 m_2 \rangle \) vanish whenever \(m \ne \mu +\mu '\). The evaluation of the latter in the last row of Eq. (277) leads to
Then, exploiting again the results in Eqs. (274) and (275), the limit in the equation can be evaluated and the expression simplified as Eq. (276), giving
Combining the last result together with the one in Eq. (276), we obtain the expression of the complete integral in Eq. (264),
By exploiting the complex-conjugation property of the regular Coulomb repulsive wavefunction \(\psi _{{\mathbf {p}}}^{(-)}({\mathbf {r}})= \psi _{-{\mathbf {p}}}^{(+)*}({\mathbf {r}})\), also the second integral in Eq. (56) can be evaluated, by noting that the latter property implies only the disappearance of a \((-1)^{\ell }\) factor in Eq. (265), that for \(\ell = 1\) is compensated by the overall minus sign in front of the integral,
Therefore, the full leading order \(T_{\mathrm {SC}}\) matrix element in Eq. (55) reads
where \(\theta \) is the scattering angle.
Three-dimensional Riemann sums
The derivation of the energy corrections from the finite volume ERE for the lowest-energy \(T_1\) scattering state implies the computation of the sum of the single and double three-dimensional Riemann series treated in this appendix.
1.1 Single sums
Let us begin with the derivation of the sum of \({\mathcal {S}}_0({\tilde{p}}) \equiv \varUpsilon \),
which can be carried out analytically. After rewriting the series over three-vectors of integers in integral form,
the Poisson summation formula for a three-dimensional Dirac delta function,
can be directly applied, obtaining
Then, the remaining integral can be computed by singling out the zero mode,
where the second integral vanishes, since the sum excludes the null vector. Equipped with the last result, it immediately follows that
Second, we report the sum of the series whose general term is given by the inverse of the norm of the three vector of integers \({\mathbf {n}}\) [40],
Even if it does not play any role in the expression of the finite volume energy corrections, the sum of the series shares its asymptotic behaviour with the one of Ϙ\(_1\). A precise determination of the sum of \({\mathcal {G}}^{(0)}\), thus, provides a benchmark test, which has to be passed successfully before addressing the Ϙ\(_{1}\) calculation. Due to the rapid oscillation of the sum of the series for similar values of the cutoff constant \(\varLambda _n\), the original series in Eq. (290) has been recast as
where \(\epsilon \) is a small real constant and the exponential factor proves to quench the oscillations of \({\mathcal {G}}^{(0)}\) for neighbouring values of \(\varLambda _n\). Considering the interval \(0.1 \le \epsilon \le 1\), the sum of the series proves to decrease monotonically towards \(\epsilon = 0\) n the \(\varLambda _n \rightarrow +\infty \) limit and the behaviour is linear with \(\epsilon \), with small quadratic corrections. The subsequent quadratic interpolation, in fact, returns a value of \({\mathcal {G}}^{(0)}\) compatible with the exact one in literatur(cf. Eq. (290) and Ref. [40]),
It follows that the chosen approach (cf. Eq. (290)) is successful in the evaluation of the sum of the series and can be promoted to more involved cases. Moreover, exploring a larger interval of \(\varepsilon \) towards larger values, further deviations form linearity are likely to appear in the fit. In particular, the following class of fitting functions,
is expected to provide a satisfactory description of the behaviour of of \({\mathcal {G}}^{(0)}\) with \(\varepsilon \) both in the vicinity of zero and in the infinite \(\varepsilon \) limit.
Correlated to \({\mathcal {G}}^{(0)}\) is the \({\mathcal {I}}^{(0)}\) series, which appears in both in the QED leading order corrections to the scattering parameters (cf. Eqs. (134)–(139)) and in the large binding momentum limit of the Lüscher functions \({\mathcal {S}}_2(\mathrm {i}{\tilde{\kappa }})\) and \({\mathcal {S}}_3(\mathrm {i}{\tilde{\kappa }})\), see eqs. (222) and (223). The sum of this series is already known in literature [40, 70, 94] and is given by
where the first equality is shown in tab. 1 and Eq. (2.61) of Ref. [70]. A precise evaluation of \({\mathcal {I}}^{(0)}\) can be attained by isolating the cutoff-dependent part of the series via the Poisson summation formula. In particular, the addition and subtraction of a \(1/(|{\mathbf {n}}|^2+1)\) term in the original series yields
where the first term on the r.h.s proves to converge in the \(\varLambda \rightarrow +\infty \) limit as fast as the \({\mathcal {J}} \equiv {\mathcal {J}}^{(0)}\) series in Ref. [94] and the linear divergence is confined into the second summation. Exploiting the Poisson formula in Eq. (285), the non-regularized series can be evaluated as follows,
where the zero \({\mathbf {n}}\) term has been added to the sum and, then, the spherical cutoff has been moved from the sum to the integral over the finite-volume momenta. Separating the zero modes from the others in the result of Eq. (294), we obtain
where the third and the fourth term on the r.h.s. turn out to be finite in the infinite cutoff limit and the last integral can be performed in the complex plane, by collecting the residues according to Jordan’s Lemma. Performing the remaining integration, in fact, the last equation becomes
an expression that can be directly plugged into Eq. (294), obtaining the desired result,

As it can be observed, the cutoff dependent term in the original series has been removed and, at the same time, two rapidly convergent sums, Ϡ\(_0 = 0.0125\) and \(\gamma _1\) (cf. Eq. (302)) replaced the divergent one, thus reducing significantly the computational efforts. The procedure is completely analogous to the one adopted in Appendix B 1 of Ref. [67] and can be applied to other cutoff-regulated single sums.
At this stage, we focus on the single sums appearing as coefficients in the \(\delta {\tilde{p}}^2\) expansion of the Lüscher functions \({\mathcal {S}}_1({\tilde{p}})\), \({\mathcal {S}}_2({\tilde{p}})\) and \({\mathcal {S}}_3({\tilde{p}})\) around \({\tilde{p}}^2 = 1\). Adopting a notation similar to the one used for Eqs. (290) and (293), the sums of relevant three-dimensional Riemann series yield
where the first three coincide respectively with \({\mathcal {I}}_1\), \({\mathcal {J}}_1\) and \({\mathcal {K}}_1\) in Appendix C of Ref. [67]. In particular, all the series not regulated by a cutoff can be computed directly, without the need to resort to the techniques outlined above. On the other hand, the sum of \({\mathcal {I}}^{(1)}\) can be obtained rapidly from the existing result for \({\mathcal {I}}^{(0)}\). In fact, the addition and subtraction of a \(1/|{\mathbf {n}}|^2\) term gives
where in the first term on the r.h.s. the limit \(\varLambda _n \rightarrow +\infty \) has been taken. Moreover, replacing \({\mathcal {I}}^{(0)}\) with its expression given in Eq. (293), the last formula can be rewritten in a compact fashion as

so that \({\mathcal {I}}^{(1)}\) can be evaluated independently from \({\mathcal {I}}^{(0)}\). Finally, we conclude the paragraph by enumerating the single series which do not appear directly in the \(\delta {\tilde{p}}^2~\sim ~0\) expansions of the Lüscher functions but that play an ancillary role in the evaluation of the single sums listed in Eqs. (298) and (301) (cf. \(\gamma _1\), \(\gamma _2\) and \(\digamma _1\)) or in the double sums in Eqs. (307) and (308) (cf. \(\digamma _1-\digamma _4\)),
and
Both the classes of series in Eqs. (300) and (301) do not display convergence issues and can be directly evaluated. Note that \(\digamma _1\) coincides with the sum listed as \(\chi _3\) in Eq. (A1) of Ref. [94].
1.2 Double sums
Differently from their single counterparts, double sums appear only in the purely Coulombic contributions in the \(\ell =1\) ERE and arise from the \({\tilde{p}}^2 \rightarrow 1\) limit of the Lüscher functions \({\mathcal {S}}_2({\tilde{p}})\) and \({\mathcal {S}}_3({\tilde{p}})\). Furthermore, the \({\tilde{p}}^2 \approx 1\) expansion of the functions \({\mathcal {S}}_2({\tilde{p}})\) and \({\mathcal {S}}_3({\tilde{p}})\) in Sect. 3.3.1 generates two categories of double sums. The simplest of them consists in one three-dimensional Riemann sum performed on \({\mathbb {Z}}^3\), followed by a sum over the six possible unit-vectors parallel to the axes of a cubic box. Adopting the notation introduced for the derivation of the of the \({\tilde{p}}^2 \approx 1\) limit of \({\mathcal {S}}_2({\tilde{p}})\) in sec. III D 2 of Ref. [94] , we write
The presence of the factor \(1/|{\mathbf {m}}-{\mathbf {n}}|^2\) in the sums \(\chi _1-\chi _4\) of Eq. (304) ensures convergence without the need for the introduction of spherical cutoffs and regulators. Besides, the sum \(\chi _0\) is analytical and denoted as \(\chi _1\) in Ref. [94], whereas the series \(\chi _2\) and \(\chi _3\) coincide with the \(\chi _2\) and \(\chi _5\), respectively, in the latter work, except for the inclusion of the zero mode in the sum over \({\mathbf {m}}\).
Another group of series belonging to the same category is provided by the sums which are not present in the expansions of the \({\mathcal {S}}_2({\tilde{p}})\) and \({\mathcal {S}}_3({\tilde{p}})\) Lüscher functions, but occur in the rewriting of certain double sums in terms of the already existing results in literature. Due to the fast convergence, the evaluation such sums does not display difficulties and gives

thus permitting a fast evaluation of \({\mathcal {R}}^{(1)}\) and \({\mathcal {R}}_{2i~2j}^{(1)}\) in terms of the existing results in Ref. [94]. Finally, of the same kind of the sums in Eqs. (304) and (305) is the series Ϙ\(_{0}\) in Eq. (203), which appears as a proportionality constant in the \({\mathcal {O}}(1/\delta {\tilde{p}}^2)\) contributions to \({\mathcal {S}}_3\) (cf. Eq. (209)) and allows for a pairwise elementary numerical evaluation,

Now we switch to the second category of double sums, the one consisting of two three-dimensional sums performed on \({\mathbb {Z}}^3\). First, we consider the series stemming from the \({\tilde{p}} \sim 1\) approximations of \({\mathcal {S}}_2({\tilde{p}})\), see Eq. (193). The latter sums, in fact, are the counterpart of divergent double integrals contributing to the amplitudes of the relevant two-particle scattering processes. Due to the large increase of the configuration space, for the numerical calculation of the sum of such series it is advisable to parallelize the operations via the development of GPU codes (e.g. in Cuda C++). The computational efforts can be significantly reduced by subdividing the original double sum into an arbitrarily large finite number of single sums, characterized by a three dimensional vector of integers. Then, assigning each of the outcoming single sums to a different subunit of a graphic card, the sum of the original double series is derived by gathering the results obtained simultaneously by each operating unit.
In particular, the series \({\mathcal {R}}^{(1)}\) in Eq. (191) can be expressed in terms of the already known \({\mathcal {R}} \equiv {\mathcal {R}}^{(0)}\) in Eq. (30) of Ref. [94]. By adding and subtracting \({\mathcal {R}}^{(0)}\) from \({\mathcal {R}}^{(1)}\) in Eq. and performing few manipulations, the latter series can be conveniently recast as

Once in this form, the sum of \({\mathcal {R}}^{(1)}\) can be obtained by exploiting the existing result for the cutoff-regularized sum \({\mathcal {R}}^{(0)}\) in Ref. [94], together with the single sums in Eqs. (303), (304) and (305). The only additional computational effort is given by the double sum explicitly shown on the r.h.s of Eq. (307), which proves to converge rapidly, differently from \({\mathcal {R}}^{(0)}\). For the last sum, in fact, an approach analogous to the one shown in Eq. (290) or to the tail-singularity separation (TSS) in Ref. [135] is recommendable. In the latter method, summarized in detail in Ref. [94], a three-dimensional Riemann sum is subdivided into an IR part, dominated by the the singularities of the summand and an UV part, expressed in the form of a three-dimensional integral and describing the behaviour of the argument of the original sum towards the infinity. As shown in the Appendix A of Ref. [135] for the sums \(\theta _{As}\) and \(\theta _{Bs}\), the TSS approach holds also for double sums regulated asymmetrically.
Second, we switch to the series of the kind \({\mathcal {R}}_{2i~2j}^{(1)}\) in Eq. (192). Even if the evaluation of such sums does not require stabilization techniques, we present for completeness the expression of \({\mathcal {R}}_{2i~2j}^{(1)}\) in terms of \({\mathcal {R}}_{2i~2j}^{(0)}\) and ancillary single and double sums:

As noticed in Ref. [94], the only contribution of such sums in the expression of the finite volume energy corrections for the lowest energy \(T_1\) eigenstate (cf. Eqs. (218) and (219)) is provided by \({\mathcal {R}}_{24}^{(1)} = {\mathcal {R}}_{42}^{(1)}\), whose explicit evaluation gives \(-93.692 (10)\).
Sum of the stabilized Ϙ\(_{1}\) series as a function of the parameter \(\epsilon \). The fitting model, marked by the continuous orange line, corresponds to \(f(\varepsilon )\) in Eq. (292) with \(a = -149.59(47)\), \(b = 0.0185484(64)\) and \(c=36.5(1.4)\). The value of the parameter b plays a crucial role in determining the sum of the series and maximizes the value of the coefficient of determination (\(R^2\)) of the fit for the considered fitting function. In particular, the R squared is equal to 0.999815, thus ensuring the reliability of the interpolation
Finally, we present the double sums arising from the \({\tilde{p}} \sim 1\) approximation of \({\mathcal {S}}_3({\tilde{p}})\) in Eq. (209), starting with the cutoff-regularized double sum Ϙ\(_{1}\) in Eq. (204). Since the argument of the sum is quadratically divergent with the spherical cutoff, it is convenient to adopt a stabilization technique for the evaluation of the sum. To this purpose, we chose to apply the approach in Eq. (290) to the cutoff-regularized sum over \({\mathbf {n}}\),

Since the \(\varepsilon \)-dependent Ϙ\(_{1}\) sums display a non-linear behaviour in the interval \(0 \le \varepsilon \le 1.1\), we choose to interpolate the data with the fitting function in Eq. (292). As shown in Fig. 7, \(f(\varepsilon )\) describes the behaviour of the sum of the stabilized series as a function of \(\varepsilon \) satisfactorily, therefore the sum of the series becomes

Conversely, the double sum Ϙ\(_{2}\) (cf. Eq. (205)) appearing at order \(\delta {\tilde{p}}^2\) in the power series expansion of \({\mathcal {S}}_3({\tilde{p}})\) can be calculated efficiently even without stabilization approaches, despite its sign-changing numerator. Its numerical evaluation yields

Analogous considerations hold for the Ϙ\(_{3}\) series (cf. Eq. (206)) emerging from the \(\delta {\tilde{p}}^4\) contributions to \({\mathcal {S}}_3({\tilde{p}})\). For large values of \(|{\mathbf {n}}|\) the series proves to converge even more rapidly than Ϙ\(_{2}\), therefore the statistical errors associated to the sum are smaller,

where the polynomials \(q_S({\mathbf {n}},{\mathbf {m}})\) and \(q_X({\mathbf {n}},{\mathbf {m}})\) (cf. Eqs. (207), (208)) in the numerator are given by
and
Lüscher functions
In this appendix, we concentrate on the derivation of the large imaginary momentum \({\tilde{p}} = \mathrm {i}{\tilde{\kappa }}\) limit of the double sum \({\mathcal {S}}_3({\tilde{p}})\) in Eq. (184), encountered in the derivation of the finite volume energy corrections for the lowest bound \(T_1\) state in Sect. 3.3.2. To this aim, we start by splitting the original Lüscher function \({\mathcal {S}}_3(\mathrm {i}{\tilde{\kappa }})\) into three parts,
where \(\varLambda _m\) is a spherical cutoff accounting for the divergence of the following sums over \({\mathbf {m}}\),
Due to the presence of a cutoff in the inner sum, the translation in momentum space operated in the \({\mathcal {S}}_2(\mathrm {i}{\tilde{\kappa }})\) case (cf. Appendix A3 in Ref. [94]) is no longer allowed in the individual sums (cf. Eqs. (316)–(318)). Nevertheless, since the purpose is the extraction of the finite and \({\tilde{\kappa }}\)-dependent contributions from each of the three double sums in Eq. (315), terms depending on nonzero powers of \(\varLambda _m\) and \(\varLambda _n\) can be neglected without loss of information for the FVECs. Therefore, we assume henceforth the limits \(\varLambda _n\), \(\varLambda _m \rightarrow +\infty \) and extract the finite parts from the sums depending on the binding momentum. Now, we consider the first of the three double sums in the last row of Eq. (315). After the translation in the momenta \({\mathbf {m}} \mapsto {\mathbf {m}} -{\mathbf {n}}\equiv {\mathbf {p}}\), we rewrite the argument of the inner sum in integral form,
Then, we apply the Poisson summation formula to the unconstrained sum over \({\mathbf {n}}\) and isolate the zero modes from the nonzero ones,
Concentrating on the first term of Eq. (320), we perform the translation in momentum space \({\mathbf {q}} \mapsto {\mathbf {q}} - {\mathbf {p}} \equiv {\mathbf {l}}\) and integrate over the angular variables associated to \({\mathbf {l}}\),
As it can be inferred, the first term on the r.h.s. of the last equation is independent on \({\tilde{\kappa }}\) and unbound, thus it can be neglected. On the other hand, the integral in the second term is finite and generates linear contributions in the binding momentum,
Moreover, the remaining sum in Eq. (321) can be evaluated by splitting it into two parts,
where, in the last step, the sum has been approximated by an integral, since the binding momentum is expected to be large, \({\tilde{\kappa }} \gg 1\). Additionally, the linearly divergent part of the radial integral has been consistently discarded. At this stage, we focus on the nonzero modes, i.e. the second term in Eq. (320). After performing the translation \({\mathbf {q}} \mapsto {\mathbf {q}} - {\mathbf {p}} \equiv {\mathbf {l}}\), we integrate over the angular variables associated to \({\mathbf {l}}\) and simplify the expression as
where \(l\equiv |{\mathbf {l}}|\) and the additional exponential factor \(e^{2\pi \mathrm {i} {\mathbf {p}}\cdot {\mathbf {n}}}\) has been dropped, since for integer momenta it is equal to one. Furthermore, the argument of the radial integral over the momenta \(|{\mathbf {l}}|\) is even, thus the integration region can be extended to the whole real axis. Additionally, the integrand tends uniformly to zero in the limit \(l \rightarrow \pm \infty \) and it is analytical all over the complex plane \(l \in {\mathbb {C}}\), except for two simple poles at \(l_{\pm } = \pm \mathrm {i} {\tilde{\kappa }}\), located along the imaginary axis. It follows that the integration region can be extended to an arbitrary large circular region about the origin of the complex plane encompassing the two singularities. Moreover, the integrand can be split into two functions of complex variable l
so that \(g_+(l)\) (\(g_-(l)\)) can be integrated in a semicircumference with arbitrarily large radius about the origin in the upper (lower) part of the complex plane picking up the \(l_+\) (\(l_-\)) singularity, according to Jordan’s Lemma. The residues associated to the two poles turn out to coincide and to depend on \(|{\mathbf {n}}|\) through negative exponentials. Observing again that \(e^{-2\pi |{\mathbf {n}}|{\tilde{\kappa }}} \le e^{-\pi {\tilde{\kappa }}} e^{-\pi |{\mathbf {n}}|}\), Eq. (324) becomes

where Ϡ\(_{1}\) is a small constant equal to 0.400982(1). Finally, we evaluate the sum over \({\mathbf {p}}\) in the same fashion as Eq. (323) and we single out the non-divergent part, finding

The finite contribution arising from the non-zero modes in Eq. (327) decays exponentially with \({\tilde{\kappa }}\), thus it is negligible in the large binding momentum regime in comparison with the one in Eq. (323). Therefore, we retain only the latter and write
Now, we switch to the second term in the last row of Eq. (315) and we observe that, in the \(\varLambda _n, \varLambda _m \rightarrow +\infty \) limits, translational symmetry is restored and \({\mathfrak {S}}_2^{\infty }\) coincides with \({\mathfrak {S}}_1^{\infty }\). As a consequence, we are allowed to write
At this stage, we can concentrate directly on the last term in the second row of Eq. (315), which can be conveniently split as follows,
so that the second term on the r.h.s. of the last equation is factorized. Since the two disentangled sums in the product are identical, it is sufficient to evaluate only one of them and, then, to take the square of the retained finite parts. As previously, we first rewrite the argument of the sum in integral form and then exploit the Poisson summation formula,
where the zero modes have been isolated. As it can be observed, the expression in the last row of Eq. (331) is identical to the one in Eq. (320) after the translation \({\mathbf {q}} \mapsto {\mathbf {q}} - {\mathbf {p}} \equiv {\mathbf {l}}\) in momentum space, except for the outer sum over \({\mathbf {p}}\) and the factor 1/2. Therefore, we are allowed to exploit the results in Eqs. (322) and (326) for zero and non-zero modes respectively, obtaining

As a consequence the second term on the r.h.s. of Eq. (330) can be finally rewritten as

where the last two terms on the r.h.s. are exponentially suppressed and they have to be neglected for consistency. Second, we switch to the single sum on the r.h.s. of Eq. (330). Introducing the integral sign and exploiting again the Poisson summation formula, the last contribution to \({\mathcal {S}}_3(\mathrm {i}{\tilde{\kappa }})\) becomes
where the zero modes have been again isolated from the non-zero ones. The first integral in Eq. (334) can be carried out after few manipulations,
Then, the integration over the angular variables associated to \({\mathbf {q}}\) in Eq. (335) gives
where \(q \equiv |{\mathbf {q}}|\). As in the case of Eq. (324), the integrand is an even function of q, thus the integration region can be extended to the whole real axis. Besides, the integrand tends uniformly to zero in the limit \(l \rightarrow \pm \infty \) and is analytical all over the complex plane \(l \in {\mathbb {C}}\), except for two double poles at \(q_{\pm } = \pm \mathrm {i} {\tilde{\kappa }}\), located along the imaginary axis. It follows that the integration region can be extended to an arbitrary large circular region about the origin of the complex plane encompassing the two singularities. Moreover, the integrand can be split into two functions of complex variable q
so that \(h_+(q)\) (\(h_-(q)\)) can be integrated in a semicircumference with arbitrarily large radius about the origin in the upper (lower) part of the complex plane picking up the \(q_+\) (\(q_-\)) singularity, according to Jordan’s Lemma. Again, the residues about the two double poles turn out to coincide and to depend on \(|{\mathbf {n}}|\) through negative exponentials,
Now, observing again that \(e^{-2\pi |{\mathbf {n}}|{\tilde{\kappa }}} \le e^{-\pi {\tilde{\kappa }}} e^{-\pi |{\mathbf {n}}|}\), the sum in Eq. (338) can be bound from above

where Ϡ\(_{2}\) is a small constant equal to 0.485647(1). It follows that the contribution of the nonzero modes associated to the single sum in the second row of Eq. (330) is exponentially suppressed and can be neglected in the large binding momentum limit. Collecting all the results in Eqs. (328), (329), (333) and (335), the large binding momentum limit of the double sum \({\mathcal {S}}_3(\mathrm {i}{\tilde{\kappa }})\) is found,
where the ellipses include the cutoff-dependent divergent terms and functions of \({\tilde{\kappa }}\) which are suppressed by negative exponentials.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Stellin, G., Meißner, UG. P-wave two-particle bound and scattering states in a finite volume including QED. Eur. Phys. J. A 57, 26 (2021). https://doi.org/10.1140/epja/s10050-020-00319-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epja/s10050-020-00319-1