Femtoscopic correlations and the $\varLambda _c N$ interaction

Abstract

We study the prospects for deducing constraints on the interaction of charmed baryons with nucleons from measurements of two-particle momentum correlation functions for $\varLambda _c p$. The correlation functions are calculated for $\varLambda _c N$ and $\varSigma _c N$ interactions that have been extrapolated from lattice QCD simulations at unphysical masses of $m_\pi =410-570$ MeV to the physical point using chiral effective field theory as guideline. In addition, we consider phenomenological $Y_c N$ models from the literature to explore the sensitivity of the results to the properties of the interaction in detail. We find that a measurement of the $\varLambda _c p$ correlation functions could indeed allow one to discriminate between strongly attractive $\varLambda _c N$ forces, as predicted by some phenomenological models, and a weakly attractive interaction as suggested by the presently available lattice simulations.

1 Introduction

Two-hadron momentum correlation functions extracted from relativistic heavy-ion collisions provide a doorway to information on the hadron-hadron interaction at low energies [1, 2], presently inaccessible by other means. This concerns especially the interaction of charmed hadrons with ordinary matter, for example the one of the charmed baryons ${\varLambda }_c$ and ${\varSigma }_c$ ($Y_c$) with nucleons. Insight into the dynamics of such systems would deepen our notion of the flavor dependence of the strong interaction, encoded on the fundamental level in quantum chromodynamics (QCD). Indeed, the understanding of the flavor dependence of hadron-hadron forces is a key element in the study of charmed dibaryons [3] and exotic hadronic molecules [4]. The lack of knowledge on the $Y_cN$ interaction also hinders progress in the long-standing issue regarding the existence of charmed nuclei [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22]—for recent reviews see [23,24,25]. These are nuclei containing a $Y_c$ hyperon, similar to the more familiar hypernuclei which are formed with a strange baryon, $\varLambda$ and/or $\varSigma$ (Y).

The discovery of $Y_c$ hypernuclei would reveal a new form of strongly-interacting matter and thereby widen our knowledge on the QCD phase diagram. It would also give hope to learn about medium effects on the phenomenon of chiral symmetry restauration, a phenomenon associated with the light quarks and sensitive to environmental effects, which a $Y_c$ would probe when bound to a nucleus [26]. Although, in principle, dedicated scattering experiments producing low-energy $Y_c$ hyperons might be feasible in the future at sites such as J-PARC [27] and KEK [28] in Japan and FAIR [29, 30] in Germany, high-energy heavy-ion experiments produce enough $Y_c$ hyperons (and nucleons, of course) to facilitate the extraction of a $Y_cN$ momentum correlation function. Given the prospects and no impediment of principle, this is a timely opportunity worth exploring.

Actually, the opportunity offered by heavy-ion collisions and/or high-energetic pp collisions has been already successfully exploited in respective investigations of the ${\varLambda }p$, ${\varSigma }^0 p$, and $\varXi ^- p$ systems [31,32,33,34,35,36]. Femtoscopic studies of the YN interaction certainly profit from the large $\varLambda$ production yields, which are much larger than those of $\varLambda _c$. Yet, recent pp, pA and AA experiments [37,38,39,40,41,42,43] discovered far greater $\varLambda _c$ yields than predicted by traditional hadronization models, which is welcome news for extracting a $Y_cN$ correlation function from such collisions. From the theoretical side, the $\varLambda _c N$ system benefits from the absence of nearby thresholds, the presence of which would require a coupled-channels approach and would also introduce further uncertainties [44, 45]. Indeed, in case of ${\varLambda }_cN$ the nearest other threshold (${\varSigma }_cN$) is separated by an energy of $M_{{\varSigma }_c} - M_{{\varLambda }_c} = 168$ MeV, whereas for YN and the ${\varLambda }N$ system it is separated by just $M_\varSigma - M_\varLambda = 78$ MeV. These positive perspectives motivate us to utilize the available theoretical information on the $Y_c N$ force to predict ${\varLambda }_cN$ momentum correlation functions with the aim to initiate pertinent femtoscopic experiments.

Most of the theoretical work on the $Y_cN$ force has been done within meson-exchange models. References [21, 46] are the most recent examples. There is also the very recent quark-model based study of Garcilazo et al. [47], and that of Maeda et al. [48], which combines both models. Although not constrained by experimental data, some of the studies do rest on symmetry principles and physical consistency. In meson-exchange models, SU(4) flavor symmetry, albeit questionable in the charm sector [49, 50], constrains the values of coupling constants. In quark models, fitting the low-lying hadron spectrum and hadron-hadron scattering observables constrains parameters such as quark masses and quark-quark forces. Nonetheless, the overall situation is certainly unsatisfactory. However, it started to change with the recent lattice QCD (LQCD) simulations by the HAL QCD Collaboration [20, 51]. The HAL QCD results are for unphysical quarks masses, corresponding to $m_\pi =410$ MeV or larger, and thus, need to be extrapolated to the physical point if one wants to see the proper physical implications. Haidenbauer and Krein [52] carried out such an extrapolation with chiral effective field theory (EFT) techniques [53, 54], following the scheme of [55,56,57] used for the YN system. The overall theoretical picture revealed by the phenomenological and lattice studies can be summarized as follows: (1) the ${\varLambda }_cN$ and ${\varSigma }_cN$ forces are attractive, (2) the ${\varLambda }_cN$ interaction from LQCD is significantly weaker than the one suggested by most phenomenological studies, (3) the strength of the ${\varLambda }_cN$ force increases noticeably when the lattice results are extrapoled to the physical point but still remains on a moderate level. Given this situation, there arises the question whether measurements of the ${\varLambda }_cN$ correlation functions could allow one to discriminate between the model results and the predictions based on/inferred from lattice simulations. In this paper, we give an affirmative answer to this question.

The paper is organized as follows. In the next section, we provide a brief overview of the formalism for evaluating two-hadron momentum correlation functions. In Sect. 3 we introduce the employed ${\varLambda }_cN$ interactions and we provide predictions for the corresponding ${\varLambda }_cp$ correlation functions. The paper closes with a Summary.

2 Correlation function

We summarize the main steps and compile the basic equations of femtoscopy to access hadron-hadron scattering information [58, 59]. The extracted observable is a correlation function $C(\mathbf {p}_1,\mathbf {p}_2)$ of measured hadron momenta $\mathbf {p}_1$ and $\mathbf {p}_2$. $C(\mathbf {p}_1,\mathbf {p}_2)$ entails a ratio of two yields: $C(\mathbf {p}_1,\mathbf {p}_2) = A(\mathbf {p}_1,\mathbf {p}_2)/B(\mathbf {p}_1,\mathbf {p}_2)$, with $A(\mathbf {p}_1,\mathbf {p}_2)$ formed by hadrons coming from the same collision (coincidence yield) and $B(\mathbf {p}_1,\mathbf {p}_2)$ formed by hadrons coming from separate events (uncorrelated yield). A $C(\mathbf {p}_1,\mathbf {p}_2)$ not equal to unity implies correlation between the detected particles; a correlation occurs due to mutual interaction and also due to quantum interference. The latter arises only for identical particles and, accordingly, is not present in the combination $Y_c$ and N.

Experimental data on $C(\mathbf {p}_1,\mathbf {p}_2)$ and their theoretical interpretation are normally discussed in terms of the center-of-mass and relative momentum coordinates, $\mathbf {P}= \mathbf {p}_1 + \mathbf {p}_2$ and $\mathbf {k}= (M_2 \mathbf {p}_1 - M_1 \mathbf {p}_2)/(M_1+M_2)$, where $M_1$ and $M_2$ are the hadron masses. In terms of these coordinates, a connection between the measured correlation function and hadron-hadron scattering can be made in the rest frame of the pair, $\mathbf {P}=0$, through the (approximately valid) Koonin-Pratt formula [1, 60]:

$$\begin{aligned} C(\mathbf {k}) = \frac{A(\mathbf {k})}{B(\mathbf {k})} \approx \int d\mathbf {r}\, S_{12} (\mathbf {r})\, |\psi (\mathbf {r},\mathbf {k})|^2 \ . \end{aligned}$$

(1)

Here $\psi (\mathbf {r},\mathbf {k})$ is the relative wave function of the pair and $S_{12}(\mathbf {r})$ a static source distribution, a relative distance distribution in the pair’s rest frame—[58, 59, 61, 62] discuss the validity of the assumptions and approximations behind this formula.

We compute the wave function $\psi (\mathbf {r},\mathbf {k})$ within the formalism described in reference [45]. To make the paper self-contained, we describe the main features of that formalism but present only those equations relevant for this study. As we elaborate in the next section, coupled channels do not play an important role, basically for the reason discussed in the Introduction. Therefore, we restrict the formal part to the single-channel case [45].

Past studies have shown that the correlations are predominantly due to the interaction in the S-waves. Accordingly, only the pertinent modifications in the S-wave part of the wave function, $\psi _{l=0}(r,k) = \psi _0(r,k)$, are taken into account so that one can write [2, 63]:

$$\begin{aligned} \psi (\mathbf {r},\mathbf {k}) = e^{i \mathbf {k}\cdot \mathbf {r}} + \psi _0(r,k) - j_0(kr) \ , \end{aligned}$$

(2)

where $j_0(kr)$ is the S-wave component of the non-interacting wave function, a spherical Bessel function. Supposing a spherically symmetric source $S_{12}(r)$, one obtains for the Koonin-Pratt formula:

$$\begin{aligned} C(k) = 1 + 4\pi \int dr \, r^2 \, S_{12}(r) \left[ |\psi _0(k,r)|^2 - |j_0(kr)|^2 \right] \ . \end{aligned}$$

(3)

One needs here the wave function $\psi _0(k,r)$ away from the asymptotic region, i.e., for $0 \le r \le \infty$. One can use either the Schrödinger equation or the Lippmann-Schwinger (LS) equation to obtain $\psi _0(k,r)$. Haidenbauer [45] uses the latter, the most convenient choice for nonlocal potentials, like those in references [22, 52]. Let $T_0(q,k;E)$ denote the S-wave component of the half-off-shell T-matrix and ${\tilde{\psi }}_0(k,r) = \exp (-2i\delta _0)\,\psi _0(k,r)$, where $\delta _0 = \delta _0(k)$ is the phase shift; then [67, 68]

$$\begin{aligned} {\tilde{\psi }}_0(k,r)= & {} j_0(kr) \nonumber \\&\quad + \frac{1}{\pi } \int dq \,q^2 \, j_0(qr)\, \nonumber \\&\quad \times \frac{1}{E-E_1(q)-E_2(q)+i\epsilon } \, T_0(q,k;E) \ , \nonumber \\ \end{aligned}$$

(4)

where $E=E_1(k)+E_2(k)$, with $E_i = \sqrt{k^2 + M^2_i}$. The normalization of $\psi _0(k,r)$ is

$$\begin{aligned} \psi _0(k,r) \xrightarrow {r\rightarrow \infty }&\frac{e^{-i\delta _0}}{kr} \sin (kr + \delta _0) \nonumber \\&= \frac{1}{2ikr}\left[ e^{ikr} - e^{-2i\delta _0} e^{-ikr}\right] , \end{aligned}$$

(5)

which differs from the most common form by an overall phase $e^{-2i\delta _0}$, an immaterial difference as one needs absolute squares only. In the case of ${\varLambda }_cN$ there are two S-waves, namely the $^1S_0$ state with total spin $S=0$ and the $^3S_1$ with $S=1$. Moreover, the latter partial wave can couple to the $^3D_1$ state via the tensor force. In the present study the coupling $^3S_1$-$^3D_1$ is taken into account when solving the LS equation and evaluating the corresponding T-matrices $T_{ll'}$ ($l,l'=0,2$), see, e.g., Polinder et al. [55]. However, in the actual calculation of the wave function according to Eq. (4), only the S-wave component $T_{00}$ is needed [45]. Standard experiments allow one to measure only an average over the $S=0$ and 1 states. It is commonly assumed that the weight is the same as for free scattering which suggests the substitution $|\psi _0|^2 \rightarrow 1/4\, |\psi _{^1S_0}|^2 + 3/4\,|\psi _{^3S_1}|^2$.

In the present study we adopt the usual approximation for the source function $S_{12}(r)$ and represent it by a Gaussian distribution which depends only on one parameter, namely the source radius R. It is given by $S_{12}(\mathbf{r} )=\exp (-r^2/4R^2)/(2\sqrt{\pi }R)^3$ in the proper normalization. In the presence of the Coulomb interaction, i.e. for $\varLambda _c p$, Eq. (2) takes on the form [64]

$$\begin{aligned} \psi (\mathbf {r},\mathbf {k}) = \varPsi ^C(\mathbf {r},\mathbf {k}) + \psi ^{SC}_0(r,k) - F_0(kr)/(kr) \ , \end{aligned}$$

(6)

where $F_l(kr)$ is the regular Coulomb wave function for $l=0$ and $\psi ^{SC}_0(r,k)$ the strong scattering wave function in the presence of the Coulomb interaction. $\varPsi ^C(\mathbf {r},\mathbf {k})$ is the full Coulomb wave function. With these quantities the correlation function C(k) can be obtained again from Eq. (3) after an appropriate substitution of the wave functions. Most importantly, one has to keep in mind that the “1” in Eq. (3) has to be replaced by $\int dr\, r^2 S_{12}(r) \int \frac{d\varOmega }{4\pi } |\varPsi ^C(\mathbf {r},\mathbf {k})|^2$ [64]. How calculations with the Coulomb interaction can be performed in momentum space is described in detail in Appendix D of reference [65]. For that the Vincent-Phatak method [66] is employed. With it the Coulomb-distorted strong T-matrix can be obtained, on- and half-off shell, by a matching condition. Then the scattering wave function $\psi ^{SC}_0(r,k)$ can be again evaluated analogous to Eq. (4).

3 Interactions and results

In this section we present our predictions for ${\varLambda }_cN$ interactions [22, 52] obtained by extrapolating lattice simulations of the HAL QCD Collaboration to the physical point (LQCD-e) . We begin with summarizing the main ingredients of the LQCD-e potential. Then, we show results for the ${\varLambda }_cp$ correlation functions obtained from that potential and study their source size dependence. In addition, we explore the sensitivity of the correlation functions to the strength of the ${\varLambda }_cN$ interaction. For that purpose we resort to results of phenomenological potentials available in the literature [21, 47, 48] for orientation. As already mentioned, in general these models suggest a more strongly attractive ${\varLambda }_cN$ force than lattice QCD and some [48] even lead to two-body bound states. It is of interest to examine the impact of such properties on the correlation function.

Table 1 Effective range parameters in the $^1S_0$ (s) and $^3S_1$ (t) partial waves. Results are presented for the $\varLambda _c N$ and $Y_cN$-A potentials inferred from LQCD and for the simulations of the potentials from [48] (CTNN-d), [21] (Model A), and [47] (CQM). For the latter the results of the original interactions are given in brackets

3.1 The ${\varLambda }_cN$-${\varSigma }_cN$ interaction

The ${\varLambda }_cN$-${\varSigma }_cN$ potential is constructed in close analogy to the ${\varLambda }N$-${\varSigma }N$ interaction developed by the Jülich-Bonn-Munich group [55,56,57] based on chiral EFT and contains contact terms and contributions from one-pion exchange. For the $^1S_0$ and $^3S_1$-$^3D_1$ partial waves of interest here, one has [52]:

$$\begin{aligned}&V_{{\varLambda }_cN}(^1\!S_0) = {\tilde{C}}_{^1\!S_0} + {C}_{^1\!S_0}\, ({p}^2+{p}'^2) \ , \end{aligned}$$

(7)

$$\begin{aligned}&V_{{\varLambda }_cN}(^3\!S_1) = {\tilde{C}}_{^3\!S_1} + {C}_{^3\!S_1}\, ({p}^2+{p}'^2) \ , \end{aligned}$$

(8)

$$\begin{aligned}&V_{{\varLambda }_cN}(^3\!D_1 -\, ^3\!S_1) = {C}_{\varepsilon _1}\, {p'}^2 \ , \end{aligned}$$

(9)

$$\begin{aligned}&V_{{\varLambda }_cN}(^3\!S_1 -\, ^3\!D_1) = {C}_{\varepsilon _1}\, {p}^2 \, , \end{aligned}$$

(10)

$$\begin{aligned}&V^{OPE}_{{Y_c N\rightarrow Y_c N}} =-f_{{Y_c Y_c\pi }}f_{{NN\pi }} \frac{\left( \mathbf{\sigma }_1\cdot \mathbf{q} \right) \left( \mathbf{\sigma }_2\cdot \mathbf{q} \right) }{ \mathbf{q}^{\,2}+m_{\pi }^2} \ . \end{aligned}$$

(11)

where $p = |\mathbf{p}\,|$ and ${p}' = |\mathbf{p}\,'|$ are the initial and final center-of-mass (c.m.) momenta, and $\mathbf{q} = \mathbf{p'} - \mathbf{p}$ the transferred momentum. The strength parameters of the contact terms, ${\tilde{C}}_{i}$ and ${C}_{i}$, the so-called low-energy constants (LECs), have been determined in reference [52] by considering the HAL QCD results for the $^1S_0$ and $^3S_1$ phase shifts at unphysical quark masses corresponding to $m_\pi =410$ MeV and 570 MeV [20] and by a subsequent extrapolation of the established potential to the physical point, guided by chiral EFT. The actual values of the LECs can be found in Table 1 of that work¹. The coupling constants for pion exchange are given by the $f_{BB'\pi } = g^{BB'}_A/2\,F_\pi$, the ratio of the axial-vector strength $g_A^{BB'}$ to the pion decay constant $F_\pi$. For the latter and for $g_A^{NN}$ the standard values [69] ($F_\pi \approx 93$ MeV, $g_A^{NN}=1.27$) are used while the others are fixed from available lattice QCD results close to the physical point, amounting to $g_A^{{\varSigma }_c{\varSigma }_c}=0.71$ [70] and $g_A^{{\varLambda }_c{\varSigma }_c}=0.74$ [71, 72]. Note that, under the assumption of isospin conservation, $f_{{\varLambda }_c{\varLambda }_c\pi } \equiv 0$. Thus, there is no direct contribution from pion exchange to the ${\varLambda }_cN$ potential at leading order [55]. However, it contributes to the ${\varLambda }_cN$ interaction of Haidenbauer and Krein [52] via the channel coupling ${\varLambda }_cN$-${\varSigma }_cN$.

In view of additional lattice results published by the HAL QCD Collaboration recently, the ${\varLambda }_cN$ interaction has been revisited [22]. The new aspect concerns information on the interaction in the ${\varSigma }_cN$ channel [51], specifically in the $^3S_1$ partial wave. It turned out that including a direct ${\varSigma }_cN$ interaction into the coupled-channel calculation has only a minor effect on the predicted ${\varLambda }_cN$ phase shifts at the energies of interest here [22]. Nonetheless, for completeness, we study the effect on the ${\varLambda }_cp$ correlation functions too. In principle, heavy quark spin symmetry would even require to take into account the $\varSigma _c^* N$ channel [48, 73, 74]. However, as argued in reference [22] (cf. Appendix), for low-energy ${\varLambda }_cN$ scattering considered here we can assume that possible effects of the $\varSigma _c^* N$ interaction are already implicitly absorbed into the ${\varLambda }_cN$ LECs.

With the interactions defined and the parameters fixed, the next step is to solve the LS equation for the quantity $T_0(q,k;E)$ [52]. With it one can reconstruct the ${\varLambda }_cN$ wave functions, utilizing Eq. (4), and then, in turn, compute the ${\varLambda }_cN$ correlation functions. The LS equation requires regularization [75, 76] for the potential of Eqs. (7)–(11). In reference [52] a cutoff scheme with the regularization function $f(p',p) = \exp \left[ -\left( p'^4+p^4\right) /\varLambda ^4\right]$ is used [55, 56] , with $\varLambda$ values 500 MeV and 600 MeV. The choice of the $\varLambda$ values is motivated by NLO studies of the ${\varLambda }N$ and ${\varSigma }N$ systems [56, 57]. The variations of the results with $\varLambda$ can be assessed from the bands in the figures below.

As said above, we want explore also in how far differences in the interaction strength as predicted by other ${\varLambda }_cN$ potentials are reflected in the pertinent correlation functions. This goal can be achieved in a simple and efficient way within our formalism. We employ the same representation for the $Y_c N$ force as for LQCD-e interaction, see Eqs. (7)–(11), but now we adjust the contact terms to the effective range parameters from the models by Maeda et al. [48], Vidaña et al. [21], and Garcilazo et al. [47]. This allows us to capture the essential features and differences such as the overall strength of the interaction and the relative strength of the singlet and triplet S-waves, and, thus, enables us to see the impact of these properties on the correlation functions. We want to emphasize that we do not need (and we do not aim at) an exact and quantitative reproduction of the results by those potentials for that purpose.

A summary of the ${\varLambda }_cN$ results is given in Table 1 and in Fig. 1. Table 1 provides an overview of the ${\varLambda }_cN$ scattering lengths a and effective range parameters r for the various interactions in the spin-singlet (s) and triplet (t) states. We use the “baryon-baryon” convention with $k \cot \delta _0 = - 1/a + r\,k^2 / 2 + ...$. The first two entries are for the LQCD-e interaction from Ref. [52] with cutoffs $\varLambda =500,\ 600$ MeV. Then corresponding results for the variant considered in reference [22] ($Y_c N$-A) are listed, which includes a direct ${\varSigma }_cN$ interaction. Finally, one can find results for the effective range parameters for our simulations of a selection of models from references [21, 47, 48], together with the original results in brackets. Results for the $^1S_0$ and $^3S_1$ phase shifts are presented in Fig. 1. From that figure one can read off the different properties immediately. It is obvious that the potential from Maeda et al. [48] (dashed lines), denoted by CTNN-d, is by far the most attractive one. It predicts bound states, as mentioned before, with binding energies of the order of that of the deuteron in both S-waves. Model A (dash-dotted lines) presented in the paper by Vidaña et al. [21], deduced from a YN meson-exchange potential of the Jülich group [77] via SU(4) symmetry arguments, suggests a strongly attractive $^3S_1$ interaction and a moderately attractive $^1S_0$ partial wave. The ${\varLambda }_cN$ interaction derived within the constituent-quark model (CQM) by Garcilazo et al. [47] (solid lines) is closest to the interaction inferred from the lattice simulations. It is slightly less attractive in the $^1S_0$ state but noticeably more attractive in the $^3S_1$ partial wave. In view of the present uncertainty in the LQCD calculations [20, 51] and in the extrapolation, estimated in reference [52] to be of the order of $\pm 0.3$ fm on the level of the ${\varLambda }_cN$ scattering lengths, the latter model is not that far apart from the present lattice predictions.

Fig. 2

${\varLambda }_cN$ phases for the $Y_c N$ potential inferred from LQCD [52]. The bands represent the cutoff variation $\varLambda = 500-600$ MeV, see text. In addition results for the simulations of the potentials from [48] (CTNN-d), [21] (Model A), and [47] (CQM) are shown

We note that the results presented above are all obtained without inclusion of the Coulomb force. Adding the Coulomb interaction leads to a small modification of the effective range parameters in case of weakly attractive hadron forces like the LQCD-e interactions [22, 52]. For example, the singlet (triplet) scattering lengths change from $-1.01$ fm ($-0.98$ fm) to $-0.97$ fm ($-0.96$ fm) when Coulomb is added to the LQCD-e (600) potential from reference [52]. There are more sizable effects for strongly attractive potentials like CTNN-d. Nonetheless, the bound states survive despite of the Coulomb repulsion, in the original model [48] and likewise in our simulation.

3.2 Results for the ${\varLambda }_cp$ correlation function

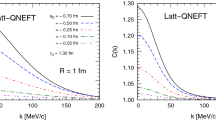
In the discussion of the correlation function we start with assessing the effects of the Coulomb interaction and of the source size. Corresponding results can be found in Fig. 2, based on the LQCD-e potential from reference [52], where we show the ${\varLambda }_cp$ correlation functions for the $^1S_0$ and $^3S_1$ partial waves separately. The choice of considered radii R of the Gaussian source is motivated by those suggested in corresponding measurements of ${\varLambda }p$ correlation functions in pp collisions at 7 TeV by the ALICE Collaboration ($R\approx 1.2$ fm) [34] and of $\varOmega p$ in central and peripheral Au+Au collisions at 200 GeV by the STAR Collaboration ($R\approx 2.5,\,5$ fm) [78].

Fig. 3

Effect of the Coulomb force and the source size R on the ${\varLambda }_cp$ correlation function. The LQCD-e potential [52] is used for the calculation

The presence of a repulsive Coulomb force in the ${\varLambda }_cp$ system leads to a strong depletion of the correlation function for small momenta. This effect is well-known and also well-documented, e.g. in calculations and precise measurements of pp correlations [34]. However, since the ${\varLambda }_cp$ interaction is much less attractive than pp, the depletion due to Coulomb is noticeable already at larger momenta and it also shifts the maximum in the correlation function to somewhat larger momenta. As a consequence the signal due to the strong interaction is significantly reduced. Nonetheless, at least for pp collisions with source radii around 1.2 fm the effect by the ${\varLambda }_cp$ interaction should be still detectable in an experiment. For heavy-ion collisions with a typical source radius around $3-5$ fm [31, 78] it looks more challenging.

Comparing the results for $^1S_0$ (top) and $^3S_1$ (bottom) one can see that they are basically identical for the LQCD-e interaction (without and with Coulomb force). This is not too surprising given that the corresponding scattering lengths and phase shifts are also almost identical, see Table 1 and Fig. 1.

Fig. 4

Difference in the $\varLambda _c p$ correlation function for the ${\varLambda }_cN$ interactions without [52] (filled band) and with a direct ${\varSigma }_cN$ interaction [22] (hatched band). Results are shown for the $^3S_1$ (top) and the spin average (bottom)

Next we compare the results for the ${\varLambda }_cN$ interactions without [52] and with a direct ${\varSigma }_cN$ interaction [22]. This is done in Fig. 3, selectively for the source radius $R=1.2$ fm. One can see that there is not much difference. Practically speaking, only the overall uncertainy, represented by the band due to the cutoff variation, is somewhat increased when additionally the influence of a direct ${\varSigma }_cN$ interaction is explicitly taken into account. Therefore, in the following we will show only the results for the potential from Ref. [52].

Fig. 5

Spin-averaged ${\varLambda }_cp$ correlation functions including the Coulomb interaction for three different source radii R. Predictions are shown for the LQCD-e interaction (band) and the simulations of CQM [47] (solid line), Model A [21] (dash-dotted line), CTNN-d [48] (dashed line). Also shown is the pure Coulomb interaction (dotted line)

Finally, we contrast the correlation functions predicted by the ${\varLambda }_cN$ potential [52] inferred from lattice results with those from (simulated) phenomenological potentials. Here we take the spin average in order to be as close as possible to the experimental situation. Corresponding results are presented in Fig. 4, again for different source sizes. Already at first sight it is clear that the different potentials considered lead to quite different predictions for the ${\varLambda }_cp$ correlation functions. Specifically, in general, more attractive interactions yield also larger correlation functions. Even the simulated CQM interaction which is only moderately more attractive than the LQCD-e interaction (cf. the ${\varLambda }_cN$ phase shifts) yields a noticeably larger maximum of C(k). This is not least due to the differences in the $^3S_1$ interaction which enters with a three-times larger weight than the $^1S_0$. The decisive role of the $^3S_1$ contribution is most prominently seen by the result for the simulated model A from reference [21], cf. dash-dotted lines in Fig. 4. The corresponding correlation function is significantly larger than those of the other considered interactions and it is still sizable for the source size $R=5$ fm. It is safe to say that even an experiment with moderate statistics should be sufficient to discriminate between that model and the properties exhibited by potentials like CQM or those inferred from lattice simulations (LQCD-e). Indeed, given that the spin dependence is not resolved in the standard measurements of correlation functions, it is primarily the strength of the spin-triplet component which can be tested, of course, always under the premises that the actual spin distribution of the produced baryons is close to the purely statistical value.

An interesting behavior is shown by the predictions based on the simulated CTNN-d interaction that supports bound states. Here there is a delicate interplay between the repulsive Coulomb interaction and the strongly attractive ${\varLambda }_cN$ potential, which produces a distinct dependence on the source radius. We believe that this characteristic behavior constitutes a rather useful signature that could help for either confirming or ruling out such bound states in experiments.

4 Summary

We studied the prospects for deducing constraints on the interaction of charmed baryons with nucleons from measurements of two-particle momentum correlation functions for $\varLambda _c p$. As a benchmark, the correlation functions have been evaluated for $\varLambda _c N$ and $\varSigma _c N$ interactions extrapolated from lattice QCD simulations by the HAL QCD collaboration [20, 51] at unphysical masses of $m_\pi =410-570$ MeV to the physical point using chiral effective field theory as guideline [22, 52]. In addition, phenomenological $Y_c N$ models from the literature [21, 47, 48] have been considered in order to explore the sensitivity to the properties of the interaction in detail. The repulsive Coulomb interaction between the positively charged $\varLambda _c$ and the proton has been taken into account in the actual calculation. Only with its effect included a meaningful and realistic estimate of the signal size that could be expected in experiments can be given.

Our studies suggest that the ${\varLambda }_cp$ correlation function is definitely a useful tool for acquiring information on the $Y_c N$ interaction. Even weakly attractive forces such as those suggested by present-day lattice simulations lead to effects that should be detectable in pertinent experiments. In case the ${\varLambda }_cN$ interaction turns out to be more strongly attractive, as predicted by some phenomenological models in the literature, then measurements of the correlation function would certainly allow one to discriminate between the different scenarios.

An open question at the moment is which yields for ${\varLambda }_cp$ one can expect in dedicated experiments. Predictions by different models for production rates at different accelerators and/or energies have been summarized in the review by the ExHIC Collaboration [79], see also Steinheimer et al. [80]. According to the review, the expected yields for ${\varLambda }_cN$ could be as large as those for $\varOmega N$. The latter channel has been already measured by the STAR [78] and ALICE [81] Collaborations. Thus, looking at the corresponding data and uncertainties might provide us a rough clue on what to expect for ${\varLambda }_cp$.