Theoretical study of spin observables in $\varvec{pd}$ elastic scattering at energies $\varvec{T_p = 800}$–$\varvec{1000}$ MeV

Abstract

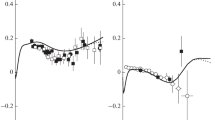
Various spin observables (analyzing powers and spin-correlation parameters) in pd elastic scattering at $T_p = 800$–1000 MeV are analyzed within the framework of the refined Glauber model. The theoretical model uses as input spin-dependent NN amplitudes obtained from the most recent partial-wave analysis and also takes into account the deuteron D wave and charge-exchange effects. Predictions of the refined Glauber model are compared with the existing experimental data. Reasonable agreement between the theoretical calculations and experimental data at low momentum transfers $|t| \lesssim 0.2$ (GeV/c)$^2$ is found for all observables considered. Moderate discrepancies found in this region are shown to be likely due to uncertainties in the input NN amplitudes. Qualitative agreement at higher momentum transfers is also found for most observables except the tensor ones with mixed x and z polarization components. Possible reasons for observed deviations of the model calculations from the data at $|t| > 0.2$ (GeV/c)$^2$ are discussed.

Appendix A: Transformation of polarization observables in \(\varvec{pd}\) elastic scattering to the Madison frame

In this appendix we give the explicit formulas which should be applied to transform the pd elastic spin observables from the $xyz = \{{\hat{q}}{\hat{n}}{\hat{k}}\}$ frame used in deriving the formalism of the refined Glauber model to the $xyz = \{{\hat{S}}{\hat{N}}{\hat{L}}\}$ (Madison) frame conventionally used in experiments (see definitions in Sect. 2).

We have the following expressions for the analyzing powers:

$$\begin{aligned} A_y^{p\,(\mathrm{Mad})}= & {} -{A_y}^p, \quad A_y^{d\,(\mathrm{Mad})} = -{A_y}^d, \nonumber \\ A_{yy}^{(\mathrm{Mad})}= & {} A_{yy}, \nonumber \\ A_{xx}^{(\mathrm{Mad})}= & {} \frac{1}{2}(1 + \mathrm{cos}\theta )\,A_{xx} + \frac{1}{2}(1 - \mathrm{cos}\theta )\,A_{zz} \nonumber \\&- \mathrm{sin}\theta \,A_{xz}, \nonumber \\ A_{xz}^{(\mathrm{Mad})}= & {} -\mathrm{cos}\theta \,A_{xz} - \frac{1}{2}\mathrm{sin}\theta \,(A_{xx} - A_{zz}), \nonumber \\ A_{zz}^{(\mathrm{Mad})}= & {} -A_{yy}^{(\mathrm{Mad})} - A_{xx}^{(\mathrm{Mad})}, \end{aligned}$$

(A.1)

and for the spin-correlation parameters:

$$\begin{aligned} C_{y,y}^{(\mathrm{Mad})}= & {} C_{y,y}, \nonumber \\ C_{x,x}^{(\mathrm{Mad})}= & {} \frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{x,x} + \frac{1}{2}(1-\mathrm{cos}\theta )\,C_{z,z} \nonumber \\&- \frac{1}{2}\mathrm{sin}\theta \,(C_{z,x} + C_{x,z}), \nonumber \\ C_{z,x}^{(\mathrm{Mad})}= & {} -\frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{z,x} + \frac{1}{2}(1-\mathrm{cos}\theta )\,C_{x,z} \nonumber \\&- \frac{1}{2}\mathrm{sin}\theta \,(C_{x,x} - C_{z,z}), \nonumber \\ C_{x,z}^{(\mathrm{Mad})}= & {} -\frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{x,z} + \frac{1}{2}(1-\mathrm{cos}\theta )\,C_{z,x} \nonumber \\&- \frac{1}{2}\mathrm{sin}\theta \,(C_{x,x} - C_{z,z}), \nonumber \\ C_{z,z}^{(\mathrm{Mad})}= & {} \frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{z,z} + \frac{1}{2}(1-\mathrm{cos}\theta )\,C_{x,x} \nonumber \\&+ \frac{1}{2}\mathrm{sin}\theta \,(C_{x,z} + C_{z,x}), \nonumber \\ C_{y,yy}^{(\mathrm{Mad})}= & {} -C_{y,yy}, \nonumber \\ C_{y,xx}^{(\mathrm{Mad})}= & {} -\frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{y,xx} - \frac{1}{2}(1 - \mathrm{cos}\theta )\,C_{y,zz} \nonumber \\&+ \mathrm{sin}\theta \,C_{y,xz}, \nonumber \\ C_{y,xz}^{(\mathrm{Mad})}= & {} \mathrm{cos}\theta \,C_{y,xz} + \frac{1}{2}\mathrm{sin}\theta \,(C_{y,xx} - C_{y,zz}), \nonumber \\ C_{y,zz}^{(\mathrm{Mad})}= & {} -C_{y,yy}^{(\mathrm{Mad})} - C_{y,xx}^{(\mathrm{Mad})}, \nonumber \\ C_{x,xy}^{(\mathrm{Mad})}= & {} -\frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{x,xy} - \frac{1}{2}(1-\mathrm{cos}\theta )\,C_{z,zy} \nonumber \\&+ \frac{1}{2}\mathrm{sin}\theta \,(C_{z,xy} + C_{x,zy}), \nonumber \\ C_{z,xy}^{(\mathrm{Mad})}= & {} \frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{z,xy} - \frac{1}{2}(1-\mathrm{cos}\theta )\,C_{x,zy} \nonumber \\&+ \frac{1}{2}\mathrm{sin}\theta \,(C_{x,xy} - C_{z,zy}), \nonumber \\ C_{x,zy}^{(\mathrm{Mad})}= & {} \frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{x,zy} - \frac{1}{2}(1-\mathrm{cos}\theta )\,C_{z,xy} \nonumber \\&+ \frac{1}{2}\mathrm{sin}\theta \,(C_{x,xy} - C_{z,zy}), \nonumber \\ C_{z,zy}^{(\mathrm{Mad})}= & {} -\frac{1}{2}(1 + \mathrm{cos}\theta )\,C_{z,zy} - \frac{1}{2}(1-\mathrm{cos}\theta )\,C_{x,xy} \nonumber \\&- \frac{1}{2}\mathrm{sin}\theta \,(C_{z,xy} + C_{x,zy}). \end{aligned}$$

(A.2)

We should note here that we did not transform the analyzing powers to the Madison frame in our previous work [31,32,33]. However, when compared the theoretical predictions to experimental data, we inverted the sign of vector analyzing powers $A_y^p$ and $A_y^d$. We also considered tensor analyzing powers $A_{yy}$ (which is the same in both coordinate frames) and $A_{xx}$ (which is changed only slightly by Eq. (A.1) in the forward hemisphere), so that there was no significant error in comparing these observables to those measured in the Madison frame. The only analyzing power that changes its behavior substantially under the transformation (A.1) is $A_{xz}$ (due to an admixture of large $A_{xx}$), which was not considered in our previous works.

The expressions for some of the above observables in terms of 18 pd amplitudes derived directly in the Madison frame and the relations of these amplitudes to our ones $A_1$–$A_{12}$ are to be found in Refs. [38, 39].

We also give here an alternative representation of the pd elastic scattering amplitude in the $\{{\hat{q}}{\hat{n}}{\hat{k}}\}$ frame, which has a more symmetric form than Eq. (4):

$$\begin{aligned} M[\mathbf{p},\mathbf{q}; {\varvec{\sigma }}, \mathbf{S}]= & {} \bigl (M_1 + M_2 \,{\varvec{\sigma }}\cdot {\hat{n}}\bigr )(1 - (\mathbf{S}\cdot {\hat{q}})^2) \nonumber \\&+ \bigl (M_3 + M_4 \,{\varvec{\sigma }}\cdot {\hat{n}}\bigr )(1 - (\mathbf{S}\cdot {\hat{n}})^2) \nonumber \\&+ \bigl (M_5 + M_6 \,{\varvec{\sigma }}\cdot {\hat{n}}\bigr )(1 - (\mathbf{S}\cdot {\hat{k}})^2) \nonumber \\&+ iM_7\,{\varvec{\sigma }}\cdot {\hat{k}}\,\mathbf{S}\cdot {\hat{k}} \nonumber \\&- M_{8}\,{\varvec{\sigma }}\cdot {\hat{q}}(\mathbf{S}\cdot {\hat{q}}\,\mathbf{S}\cdot {\hat{n}} + \mathbf{S}\cdot {\hat{n}}\,\mathbf{S}\cdot {\hat{q}}) \nonumber \\&- i\bigl (M_9 + M_{10}\,{\varvec{\sigma }}\cdot {\hat{n}}\bigr )\mathbf{S}\cdot {\hat{n}} + iM_{11} \,{\varvec{\sigma }}\cdot {\hat{q}}\,\mathbf{S}\cdot {\hat{q}} \nonumber \\&- M_{12} \,{\varvec{\sigma }}\cdot {\hat{k}}(\mathbf{S} \cdot {\hat{k}}\,\mathbf{S}\cdot {\hat{n}} + \mathbf{S}\cdot {\hat{n}}\,\mathbf{S}\cdot {\hat{k}}). \end{aligned}$$

(A.3)

The set of invariant amplitudes $M_1$–$M_{12}$ (multiplied by a standard normalization factor $8p\sqrt{\pi s}$) was used in, e.g., Refs. [21, 22] (note, however, that the direction of the unit vector ${\hat{n}}$ was chosen there opposite to ours). These amplitudes are related to our ones, $A_1$–$A_{12}$, as follows:

$$\begin{aligned} A_1= & {} M_1 + M_3 - M_5, \quad A_2 = M_2 + M_4 - M_6, \nonumber \\ A_3= & {} M_5 - M_1, \quad A_4 = M_6 - M_2, \nonumber \\ A_5= & {} M_5 - M_3, \quad A_6 = M_6 - M_4, \nonumber \\ A_7= & {} iM_7, \quad A_8 = -M_8, \quad A_9 = -iM_9, \nonumber \\ A_{10}= & {} -iM_{10}, \quad A_{11} = iM_{11}, \quad A_{12} = -M_{12}. \end{aligned}$$

(A.4)

The pd elastic observables expressed in terms of the amplitudes $M_1$–$M_{12}$ look simpler than those given by Eq. (4) of Ref. [31] and Eq. (8) of the present paper. In particular, interference between different amplitudes vanishes in the expression for the differential cross section. On the other hand, such a representation is less transparent in the sense that there are three large amplitudes $M_1$, $M_3$ and $M_5$ instead of only one dominant amplitude $A_1$ at low momentum transfers.