Abstract—
In the former two parts (Logofet et al., 2017, 2018), we reported on a matrix model for a local population of Eritrichium caucasicum, a herbaceous short-lived perennial, at high altitudes of north-western Caucasus. The model was constructed and calibrated in accordance with the observations on permanent plots in the period 2009–2014. The temporal variability of the data predetermined the temporal variations among the vital rates of the local population, too,—the elements of the “annual” matrices that project the vector, x(t), of the stage structure observed at the year t to the similar vector observed at the year t + 1. Quantitative measure of the local population fitness was calculated as the dominant eigenvalue, λ1(G), of the matrix G—the pattern-geometric average of five annual matrices—and it turned out to be greater than 1, i.e., gave a positive forecast of the population viability. After the expansion of the time series with the 2015–2017 data (presented in this article), the forecast has reversed, although the corresponding offset in λ1(G) has not been more than 16%. An alternative mode of prediction is based on the (upper and lower) estimates of the stochastic growth rate (λS) of the population in a random environment, which has been formed in the model by a random choice from 8 annual matrices distributed equally probable and independent of the choice made at the previous step. All the estimates of λS turn out to be lower than λ1(G), hereby confirming the negative viability prediction; however, a too simple model of the random environment needs further development and links to potential changes in the local habitat.

Similar content being viewed by others
REFERENCES
Caswell, H., Matrix Population Models: Construction, Analysis, and Interpretation, Sunderland, MA: Sinauer, 2001, 2nd ed.
COMPADRE, Plant Matrix Database. http://www.compadre-db.org/. Accessed March 25, 2019.
Cushing, J.M. and Yicang, Z., The net reproductive value and stability in matrix population models, Nat. Resour. Model., 1994, vol. 8, no. 4, pp. 297–333.
Dobronets, B.S., Interval’naya matematika (Interval Mathematics), Krasnoyarsk: Krasn. Gos. Univ., 2004.
Elumeeva, T.G., Onipchenko, V.G., Egorov, A.V., Khubiev, A.B., Tekeev, D.K., Soudzilovskaia, N.A., and Cornelissen, J.H.C., Long-term vegetation dynamic in the Northwestern Caucasus: which communities are more affected by upward shifts of plant species? Alp. Bot., 2013, vol. 123, no. 2, pp. 77–85.
Keyfitz, N., Introduction to the Mathematics of Population, Reading, MA: Addison-Wesley, 1977.
Li, C.-K. and Schneider, H., Application of Perron–Frobenius theory to population dynamics, J. Math. Biol., 2002, vol. 44, pp. 450–462.
Logofet, D.O., Svirezhev’s substitution principle and matrix models for dynamics of populations with complex structures, Zh. Obshch. Biol., 2010, vol. 71, no. 1, pp. 30–40.
Logofet, D.O., Complexity in matrix population models: polyvariant ontogeny and reproductive uncertainty, Ecol. Complexity, 2013a, vol. 15, pp. 43–51.
Logofet, D.O., Projection matrices revisited: a potential-growth indicator and the merit of indication, J. Math. Sci., 2013b, vol. 193, no. 5, pp. 671–686.
Logofet, D.O., Aggregation may or may not eliminate reproductive uncertainty, Ecol. Model., 2017, vol. 363, pp. 187–191.
Logofet, D.O., Averaging the population projection matrices: heuristics against uncertainty and nonexistence, Ecol. Complexity, 2018, vol. 33, no. 1, pp. 66–74.
Logofet, D.O., Ulanova, and Belova, I.N., Two paradigms in mathematical population biology: an attempt at synthesis, Biol. Bull. Rev., 2012, vol. 2, no. 1, pp. 89–104.
Logofet, D.O., Ulanova, and Belova, I.N., Adaptation on the ground and beneath: does the local population maximize its λ1? Ecol. Complexity, 2014, vol. 20, pp. 176–184.
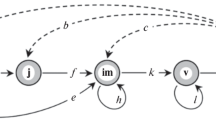
Logofet, D.O, Belova, I. N., Kazantseva, E. S., and Onipchenko, V. G., Local population of Eritrichium caucasicum as an object of mathematical modeling. I. Life cycle graph and a nonautonomous matrix model, Biol. Bull. Rev., 2017, vol. 7, no. 5, pp. 415–427.
Logofet, D.O, Belova, I. N., Kazantseva, E. S., and Onipchenko, V. G., Local population of Eritrichium caucasicum as an object of mathematical modeling. II. How short does the short-lived perennial live? Biol. Bull. Rev., 2018, vol. 8, no. 3, pp. 193–202.
Marcus, M. and Mink, H., A Survey of Matrix Theory and Matrix Inequalities, Boston: Allyn and Bacon, 1964.
MathWorks, Documentation. http://www.mathworks.com/help/optim/ug/fmincon.html?s_tid=srchtitle. Accessed December 14, 2016.
MathWorks, Documentation. https://www.mathworks.com/help/matlab/ref/rand.html?s_tid=doc_ta. Accessed February 15, 2017.
MathWorks, Documentation. https://www.mathworks.com/help/symbolic/sym.html?s_tid=doc_ta. Accessed March 16, 2018.
Oseledec, V.I., A multiplicative ergodic theorem. Ljapunov characteristic numbers for dynamical systems, Trans. Moscow Math. Soc., 1968, vol. 19, pp. 197–231.
Popov, M.G., Boraginaceae family, in Flora SSSR (Flora of the USSR), Shishkin, B.K., Ed., Moscow: Akad. Nauk SSSR, 1953, vol. 19.
RFBR, Results of the 2013 competition, http://www.rfbr.ru/rffi/ru/project_search/o_1890907. Accessed September 20, 2014.
Svirezhev, Yu.M. and Logofet, D.O., Stability of Biological Communities, Moscow: Mir, 1983.
Toräng, P., Ehrlé, J., and Ågren, J., Linking environmental and demographic data to predict future population viability of a perennial herb, Oecologia, 2010, vol. 163, no. 1, pp. 99–109.
Tuljapurkar, S.D., Population Dynamics in Variable Environments, New York: Springer-Verlag, 1990.
Tuljapurkar, S.D., Horvitz, C.C., and Pascarella, J.B., The many growth rates and elasticities of populations in random environments, Am. Nat., 2003, vol. 162, no. 4, pp. 489–502.
Funding
This study was supported in the field data mining part by the Russian Foundation for Basic Research, project no. 14-04-00214; in the modeling part by project nos. 16-04-00832 and 19-04-01227. Data processing and writing texts with the support by the Russian Science Foundation, project no. 14-50-00029.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
Conflict of interest. The authors declare that they have no conflict of interest.
Statement of the welfare of animals. This article does not contain any studies involving animals or human participants performed by any of the authors.
Additional information
Translated by D. Logofet
Appendices
APPENDIX A
Problem of Pattern-Geometric Average for Given PPMs
The averaging method using representation (8) is based on solving the problem of pattern-geometric averaging of the eight transition matrices, Tj = Lj(a, b) – Fj(a, b), for the matrices Lj(a, b) presented in Table 3 (Logofet et al., 2018). This solution is the best approximation to the exact solution of the matrix averaging Eq. (7) where the uniquely calibrated matrices Tj are involved instead of parametric matrices Lj(a, b):
In other words, it is a set of seven positive parameters c, d, e, f, h, k, l that provides the minimum to the quadratic sum of deviations from zero over all the 7 non-trivial elements of the matrix difference in the left-hand side of Eq. (A1), or formally,
Here, || … || denotes the Euclidean norm, while the exact form of the product T7…T0, which is a positive matrix obtained in rational numbers by means of machine symbolic algebra, is too cumbersome to be presented in the publication. In the digital form, we have
In the constraint minimization problem (A2), the above parameters c, …, l are the variables, whose set, \(\mathbb{B}\), of feasible values is a polyhedron in \(\mathbb{R}_{ + }^{7}\) obtained from the following considerations. Being certain fractions in accordance with their demographic sense, the parameters c, …, l put the polyhedron \(\mathbb{B}\) inside the unit cube in \(\mathbb{R}_{ + }^{7}\) , while the constraints of Tpg column subtochasticity, i.e.,
define its faces along with additional natural constraints
where the operation .≤ means element-wise comparison and minT = min{T0, T1, …, T7}, maxT = max{T0, T1, …, T7} are found element by element from Table 3.
We find solution to the problem (A2)–(A4) using the library function fmincon(…) in the Matlab computing environment (MathWorks, 2016). Its formal syntax (ibid.) suggests that the input argument of the function to be minimized (norm (A2) in our case) is a column vector rather than a square matrix. Therefore, the author’s function G2gveс(G) extracts seven variables c, …, l from the argument G (which is a 4 × 4 matrix with the pattern of matrix T (2)) and makes of them a (7 × 1) vector g. Inverse operation, i.e., recovering a 4 × 4 matrix G from vector g, is performed by the author’s function gvec2G(g). The evidence that the author’s Matlab programming has been correct is given by the operations of logical comparison:
the results of which consistently coincide with a 4 × 4 matrix and a 7 × 1 vector of units, respectively, for an arbitrarily selected matrix G of pattern (2) and vector g of dimension 7.
The norm (A2) was calculated by the function normG8_ProT of the vector argument, while the substochasticity constrains were set as Ag ≤ B using the logical 3 × 7 matrix A and the 3 × 1 vector B constraints were 3 × 7 and the vectors B 3 × 1. The following Matlab string:
launched the constraint minimization procedure after appropriate adjustment of technical optimization parameters (MathWorks, 2016); the entry “[], [],” means the absence of equality constraints in the problem formulation, vector g is a (local) solution found for the problem, FVAL is the corresponding minimum value of the function normG8_ProT.
A diverse (randomly generated) choice of the initial vector g0 gave different local solutions g, and the differences in the quality of approximation (FVAL values) reached two orders of magnitude. The value of FVAL = 5.6504… × 10–7, close to the global minimum, was reached at g0 = [1 1 1 1 1 1 1]T/10, after which the repeated search started from the just-found solution g improved FVAL down to 5.192… × 10–7, the global minimum achievable at
(with an accuracy up to 10–6), i.e., in an internal point of polyhedral \(\mathbb{B}\).
APPENDIX B
Averaging the Reproductive Uncertainty
As before (Logofet et al., 2018), the uncertain reproduction rates a(t) and b(t) are interval numbers with certain intervals of values (Table 3) given as [0, α] and [0, β ], respectively. The lower bounds of all intervals are zero, and the upper bounds α and β, depending on t, are determined from the canonical equation,

of the straight line segment connecting points (α, 0) and (0, β) in the plane (a, b). For any t, Eq. (B1) can be easily obtained by an elementary transformation of the linear relation given in Table 6. The mean-over-t values of the boundaries α and β, obtained by the rules of arithmetic operations with interval numbers (Dobronets, 2004, p. 9), are presented in the penultimate line of Table 6; their approximations by rational numbers within observable limits and, accordingly, the reconstructed averaging of Eq. (3) is in the last line.
APPENDIX C
Calculating the Stochastic Growth Rate of the E. caucasicum Local Population by a Monte Carlo Method in the MATLAB Environment
The stochastic growth rate, λS, of the population in a random environment is defined by formula (14.43) from H. Caswell (2001, p. 393) as a discrete analog of the main “Lyapunov characteristic index” for the continuous-time dynamical system (Oseledets, 1968). In formula (14.43), the denominator τ is lost, and its correct form is presented below:
Computer experiments by a Monte Carlo technique in a Matlab environment are provided by a built-in function, rand, a generator of pseudo-stochastic numbers uniformly distributed on the [0, 1] segment (MathWorks, 2017). The developers do not report on the power of this generator, but the test of repetition in the sequence of generated numbers by means of the following MATLAB-string:
>> rng(‘default’); n_equal=1; r1=rand; for nor=1:1e11, if rand==r1, n_equal=[n_equal,nor]; end; end; [nor, n_equal]
ans = 1.0000e+11 1
has not revealed any repretition in the sequece of 100 billion numbers long (69 minute work of the 2.7 GHz Intel Core i7 processor).
According to definition (C1), the value of λS is to be calculated from the limit of sequence log N(τ) as τ → ∞. If we estimate the limit value as a finite member of the sequence, then the estimate will be as closer to the true limit value as greater be the serial number of the member. However, the following obstacle occurs against the unlimited increase of this number in the course of computer experiment: since the next value, N(τ + 1), is obtained from the current vector x(τ) by its multiplying with a matrix L(τ) chosen randomly from a finite set of annual PPMs the most of which have λ1 < 1 (Table 3), a great enough number of multiplications with such matrices turns the meaningful value of vector x(τ + 1) into the machine zero, thus depriving the estimate of any sense. The longer the sequence of random matrices, the greater the probability that the computer zero does appear in its next realization. To avoid computer zeros, thereby improving the estimation accuracy, we can normalize the current vector x(τ) by a “scaling factor” (coef < 1), while compensating the great number of divisions with this factor by the multiplication with the proper power of it (after the sequence has been stopped). But the potential of such a trick is far not unlimited since a great enough number of divisions with a number less than 1 leads to the computer infinity, hence uncertainty in the logarithm calculation. The average of [λ1(Tpg)min, λ1(G)max] gives an efficient approximation to the feasible value of coef, thereafter we are searching for the feasible value by successively selecting its significant digits (see Footnote1) to Table 5) in the course of repeatedly testing the very same sequence that have generated the computer zero.
To reduce the time to be really spent for the checks, it is necessary to “instantly” get the member of the rand-sequence with a given number, and this task is coped with by an original function:
function x = norand(n)
% norand(n) returns the n-th rand;
% @ D.O.Logofet, 2017
rng('default'); % initiual 'seed'
for i = 1:n, x = rand; end
In each of the two series of experiments (described in the Methods Section), after having randomly selected the PPM number from 8 possible ones and randomly choosen the value of parameter a, the value of b is calculated from the corresponding linear relationship (Table 3).
In terms of MATLAB, this logic is naturally reproduced by defining the matrices in symbolic form (MathWorks, 2018) with uncertain parameters a and b and calculating the current vector x(τ) (in digital form) right after choosing the numerical value of these parameters. However, it turned out that functions with symbolic calculations work unacceptably long in Monte Carlo experiments. The accelerations have been achieved by replacing the input 3-dimensional array of symbolic matrices Lj (j = 0, …, 7, Table 3) with two numerical arguments: a 3-dimensional array of matrices Tj from the representation Lt = Tt + Ft plus an array of size 8 × 3 composed of the maximum values of parameter a and the ensuing coefficients of the linear relationship for b.
Rights and permissions
About this article
Cite this article
Logofet, D.O., Kazantseva, E.S., Belova, I.N. et al. Local Population of Eritrichium caucasicum as an Object of Mathematical Modelling. III. Population Growth in the Random Environment. Biol Bull Rev 9, 453–464 (2019). https://doi.org/10.1134/S2079086419050050
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S2079086419050050