1 INTRODUCTION

Since the emergence of coronavirus in Wuhan in 2019, the scientific community has been making efforts to understand and defeat the Coronavirus disease (COVID-19) [1–3]. This infectious disease, caused by the pathogen coronavirus SARS-CoV-2, was widely spread across the world’s nations by asymptomatic and pre-asymptomatic individuals who travelled unrestricted to other nations [4–6]. The manner in which COVID-19 has been spreading within the different nations of the world varies with the differences in each nation’s economic, social, and geographical structures. Owing to its high rate of propagation, COVID-19, within a wholly susceptible population, has been known to lead to a break down in health care systems. Places such Italy, Milan and New York city are examples of cities and countries whose hospitals were overwhelmed by the virus. In most countries, the first COVID-19 case were found in major cities since the population there is well-travelled. It is clear, therefore, that to understand how COVID-19 hot-spots are formed, it is vital understand the movement of individuals between different communities. Decisions regarding the relaxation or tightening of lockdown rules are dependent on a good understanding and accurate prediction of the spread of COVID-19. Hence, several models have been developed to gain insights into the dynamics of COVID-19 [3, 8–14]. Due to the inclusion of the nonlocality effect into the formulation of the model, the use of ordinary differential equations will inevitably lead to inaccurate results. We mitigate for this problem by using fractional calculus throughout this paper. Fractional operators representing dissipative effects or damage are important considerations for modelling real-world problems [15–17]. Caputo and Fabrizio [18] defined a fractional operator using the exponential decay function without singular kernel, whilst Losada and Nieto [19] investigated the properties the fractional operator as defined in [18]. Recently, Atangana and Baleanu suggested two fractional operators with non-singular and non-local kernel in Liouville–Caputo and Riemann–Liouville sense based on the generalized Mittag–Leffler function. These operators serve to describe better complex physical problems that follow simultaneously, the power and exponential decay law [13, 21–24].

Therefore, the purpose of this study is to develop a COVID-19 model that considers the stochastic nature of the disease spread, present Atangana–Seda modified schemes for the stochastic model and use these schemes to provide numerical solutions for the model with different fractional operators.

The manuscript is organized as follows: In Section 2 we give mathematical preliminaries. In Section 3 we give a mathematical model that describes the spread of COVID-19 pandemic and a stochastic version in Section 4 with mathematical analyses. Section 5 presents the numerical simulations using two different operators and, finally, a brief conclusion in Section 6.

2 MATHEMATICAL PRELIMINARIES

Here, we give some mathematical definition for differential and integral operators with singular and nonsingular kernels as follows. Thus, the fractional derivatives with Mittag–Leffer/power law and exponential decay are given below as in [11]:

Definition 1.

$$_{0}^{C}D_{t}^{\chi }g\left( t \right) = \frac{1}{{\chi \left( {1 - \chi } \right)}}\int\limits_0^t {\frac{d}{{d\varsigma }}g\left( \varsigma \right){{{(t - \varsigma )}}^{{ - \chi }}}d\varsigma } ,$$
(1)
$${}_{0}^{{cf}}D_{t}^{\chi }g\left( t \right) = \frac{{\mathcal{M}\left( \chi \right)}}{{1 - \chi }}\int\limits_0^t {\frac{d}{{d\varsigma }}g\left( \varsigma \right){{e}^{{\left[ { - \frac{\chi }{{1 - \chi }}\left( {t - \chi } \right)} \right]}}}d\varsigma } ,$$
(2)
$$_{0}^{{\mathcal{A}\mathcal{B}\mathcal{C}}}D_{t}^{\chi }g\left( t \right) = \frac{{\mathcal{A}\mathcal{B}\left( \chi \right)}}{{1 - \chi }}\int\limits_0^t {\frac{d}{{d\varsigma }}g\left( \varsigma \right){{E}_{\chi }}\left[ { - \frac{\chi }{{1 - \chi }}\left( {t - \chi } \right)} \right]d\varsigma .} $$
(3)

Next, we give the fractional integrals with Mittag–Leffler kernel, exponential decay and power law as follows:

$$_{0}^{C}J_{t}^{\chi }g\left( t \right) = \frac{1}{{\chi \left( \chi \right)}}\int\limits_0^t {{{{(t - \varsigma )}}^{{\chi - 1}}}g\left( \varsigma \right)d\varsigma } ,$$
(4)
$$_{0}^{{cf}}J_{t}^{{\chi ,\beta }}g\left( t \right) = \frac{{1 - \chi }}{{\mathcal{M}\left( \chi \right)}}g\left( t \right) + \frac{\chi }{{\mathcal{M}\left( \chi \right)}}\int\limits_0^t {g\left( \varsigma \right)d\varsigma } ,$$
(5)
$$_{0}^{{\mathcal{A}\mathcal{B}}}J_{t}^{{\chi ,\beta }}g\left( t \right) = \frac{{\left( {1 - \chi } \right)}}{{\mathcal{A}\mathcal{B}\left( \chi \right)}}g\left( t \right) + \frac{\chi }{{\mathcal{A}\mathcal{B}\left( \chi \right)\chi \left( \chi \right)}}\int\limits_0^t {{{{(t - \varsigma )}}^{{\chi - 1}}}g\left( \varsigma \right)d\varsigma } .$$
(6)

The benefits of fractional order integrals/derivatives over the classical integrals/derivatives are that we obtain extra degrees of freedom by using fractional order integrals, and the fractional order derivatives have a memory property that classical derivatives lack. It is observed from the definition of the nonsingular operator, given in Eq. (1) in [27] that the derivative at a point \(t\) is dependent on all the information within the interval \(\left[ {\alpha ,t} \right]\). The classical derivative operator only depends on \(t\), and thus has no memory. Polynomials such as \({{(t - a)}^{{\beta - 1}}}\) integrate to the function \(\frac{{{{\Gamma }}\left( \beta \right)}}{{{{\Gamma }}\left( {\alpha + \beta } \right)}}{{(t - a)}^{{\beta - 1}}},\) whilst \({{e}^{{\lambda t}}}\) integrates to \({{\lambda }^{{ - \alpha }}}{{e}^{{\lambda t}}}\), where \(\mathcal{R}e\left( \lambda \right) > 0\). For trigonometric functions, \(\sin \lambda t\) integrates to \({{\lambda }^{{ - \alpha }}}\sin \left( {\lambda t - \frac{{\alpha \pi }}{2}} \right)\), whereas a product of an exponential and trigonometric function \({{e}^{{\lambda t}}}{\kern 1pt} \cos \lambda t\) integrates to the following

$$\frac{{{{e}^{{\lambda t}}}}}{{{{{\left( {{{\lambda }^{2}} + {{\gamma }^{2}}} \right)}}^{{\alpha /2}}}}}\cos \left( {\gamma t - \alpha \phi } \right),\quad \gamma > 0,\quad \phi = \arctan \left( {\frac{\gamma }{\lambda }} \right).$$

It is observed that the extra degree of freedom in polynomials is used to control both the scale and shape parameter, whilst for the exponential graphs, the extra degree of freedom is used to change the scale of the graph. For trigonometric functions, the extra degree of freedom is used to control the location and the scale of the graph. In the case of product of a trigonometric function and an exponential function, we observe that the fractional order derivative/integral introduces a new location and scale parameter. These extra degrees of freedom are useful in fitting our models to data with a greater degree of accuracy.

3 COVID-19 MATHEMATICAL MODEL

We study the spread of COVID-19 using by considering the human population sub-divided into five distinct classes given in Table 1 with the descriptions of the state variables and parameters. The transmission rate function, which considers the Infectious classes is given by:

$$\lambda = \beta \left( {I\left( t \right) + {{\theta }_{1}}T\left( t \right) + {{\theta }_{2}}A\left( t \right)} \right),$$

where θ1 and θ2 are the modification parameters for infectiousness. Note that the individuals in the class T are in controlled environments hence they have a reduced infectiousness compared to those in the class A. Therefore \(0 \leqslant {{\theta }_{1}} \leqslant {{\theta }_{2}} \leqslant 1\).

Table 1. Model state variables and parameters descriptions
Full size table

The model flow diagram is given in Fig. 1. The nonlinear ordinary differential equations is obtained by combining the descriptions in Table 1, model Fig. 1 and assumptions is given as follows:

$$\left. {\begin{array}{*{20}{l}} {{{S}_{c}}}& = &{\pi - \lambda {{S}_{c}} - \mu {{S}_{c}}} \\ {E{\kern 1pt} }& = &{\lambda S - {{Q}_{1}}E} \\ I& = &{\sigma \rho E - {{Q}_{2}}I} \\ A& = &{\sigma \left( {1 - \rho } \right)E - \mu A} \\ {T{\kern 1pt} }& = &{{{\nu }_{1}}I - {{Q}_{3}}T,} \end{array}} \right\}$$
(7)

where \({{Q}_{1}} = \left( {\mu + \sigma } \right)\), \({{Q}_{2}} = \left( {\mu + {{\nu }_{1}} + {{\nu }_{2}}} \right)\), \({{Q}_{3}} = \alpha + \mu \), with the initial conditions

$${{S}_{c}}\left( 0 \right) > 0,\quad E\left( 0 \right) \geqslant 0,\quad I\left( 0 \right) \geqslant 0,\quad A\left( 0 \right) \geqslant 0,\quad T\left( 0 \right) \geqslant 0,\quad R\left( 0 \right) \geqslant 0$$
(8)

and the recovered class is redundant. We assume that all the model parameters nonnegative over the modelling time.

Fig. 1.
figure 1

COVID-19 model flow chart.

Full size image

4 THE STOCHASTIC MODEL USING ABC

Through the introduction of white noise from the environment, the deterministic model (7) is converted into a stochastic model using the approach as in [11, 25]. This is achieved by adding nonlinear perturbations into each equation of the system known as white noise (that is, the derivative of Brownian motion). See [11] for full discussion on impact of white noise on for the existence of stochastics process for ordinary differential equations We perturb only the rate of each class as shown below

$$\begin{aligned} {{S}_{c}}\left( t \right){\kern 1pt} :\quad - {\kern 1pt} \lambda \to \quad - {\kern 1pt} \lambda + \left( {{{{{\Lambda }}}_{{11}}}{{S}_{c}} + {{{{\Lambda }}}_{{12}}}} \right){{\beta }_{1}}\left( t \right), \\ E\left( t \right){\kern 1pt} :\quad - {\kern 1pt} \sigma \to \quad - {\kern 1pt} \sigma + \left( {{{{{\Lambda }}}_{{21}}}{{S}_{c}} + {{{{\Lambda }}}_{{22}}}} \right){{\beta }_{2}}\left( t \right), \\ ~I\left( t \right){\kern 1pt} :\quad - {\kern 1pt} {{\nu }_{1}} \to \quad - {\kern 1pt} {{\nu }_{1}} + \left( {{{{{\Lambda }}}_{{31}}}{{S}_{c}} + {{{{\Lambda }}}_{{32}}}} \right){{\beta }_{3}}\left( t \right), \\ A\left( t \right){\kern 1pt} :\quad - {\kern 1pt} \mu \to \quad - {\kern 1pt} \mu + \left( {{{{{\Lambda }}}_{{41}}}{{S}_{c}} + {{{{\Lambda }}}_{{42}}}} \right){{\beta }_{4}}\left( t \right), \\ T\left( t \right){\kern 1pt} :\quad - ~\alpha \to \quad - {\kern 1pt} \chi + \left( {{{{{\Lambda }}}_{{51}}}{{S}_{c}} + {{{{\Lambda }}}_{{52}}}} \right){{\beta }_{5}}\left( t \right). \\ \end{aligned} $$

In the above equation, \({{\beta }_{j}}\left( t \right)s~\) represents the standard Brownian motions and \({{\Lambda }_{{jk}}}\) for \(j,k = 1,..5\) are positive and denotes the intensities of environmental random perturbation as described in [11, 25]. Therefore, the stochastic model is given by:

$$\left. \begin{aligned} d{{S}_{c}} = \left[ {\pi - \left( {\lambda + \mu } \right){{S}_{c}}} \right]dt + \left( {{{\Lambda }_{{11}}}{{S}_{c}} + {{\Lambda }_{{12}}}} \right){{S}_{c}}~d{{\beta }_{1}}\left( t \right) \\ dE = \left[ {\lambda {{S}_{c}} - {{Q}_{1}}E} \right]dt + \left( {{{\Lambda }_{{21}}}E + {{\Lambda }_{{22}}}} \right)E~d{{\beta }_{2}}\left( t \right) \\ dI = \left[ {\sigma \rho E - {{Q}_{2}}I} \right]dt + \left( {{{\Lambda }_{{31}}}I + {{\Lambda }_{{32}}}} \right)I~d{{\beta }_{3}}\left( t \right) \\ dA = \left[ {\sigma \left( {1 - \rho } \right)E - \mu A} \right]dt + \left( {{{\Lambda }_{{41}}}A + {{\Lambda }_{{42}}}} \right)A~d{{\beta }_{4}}\left( t \right) \\ dT = \left[ {{{\nu }_{1}}I - {{Q}_{3}}T} \right]dt + \left( {{{\Lambda }_{{11}}}T + {{\Lambda }_{{12}}}} \right)T~d{{\beta }_{5}}\left( t \right). \\ \end{aligned} \right\}$$
(9)

Therefore, the stochastic model is given by.

4.1 Uniqueness and Existence of Solutions in Stochastic Fractional Using Atangana–Baleanu

We show that the solutions to the model (9) exists and is unique. For the sake of simplicity, we set

$$\begin{aligned} d{{S}_{c}} = {{G}_{1}}\left( {t,{{S}_{c}},E,I,A,T} \right)dt + {{H}_{1}}\left( {t,{{S}_{c}}} \right)d{{\beta }_{1}}t, \\ dE = {{G}_{2}}\left( {t,{{S}_{c}},E,I,A,T} \right)dt + {{H}_{2}}\left( {t,{{S}_{c}}} \right)d{{\beta }_{2}}t, \\ dI = {{G}_{3}}\left( {t,{{S}_{c}},E,I,A,T} \right)dt + {{H}_{3}}\left( {t,{{S}_{c}}} \right)d{{\beta }_{3}}t, \\ dA = {{G}_{4}}\left( {t,{{S}_{c}},E,I,A,T} \right)dt + {{H}_{4}}\left( {t,{{S}_{c}}} \right)d{{\beta }_{4}}t, \\ dT = {{G}_{5}}\left( {t,{{S}_{c}},E,I,A,T} \right)dt + {{H}_{5}}\left( {t,{{S}_{c}}} \right)d{{\beta }_{5}}t. \\ \end{aligned} $$

In order to proof that, we convert the equation (9) into a Volterra integral given as follows:

$$\begin{aligned} {{S}_{c}}\left( t \right) = {{S}_{c}}\left( 0 \right) + \int\limits_0^t {{{G}_{1}}\left( {\varsigma ,{{S}_{c}},E,I,A,T} \right)d\varsigma } + \int\limits_0^t {{{H}_{1}}\left( {\varsigma ,{{S}_{c}}} \right)d{{\beta }_{1}}\left( \varsigma \right)} , \\ E\left( t \right) = E\left( 0 \right) + \int\limits_0^t {{{G}_{2}}\left( {\varsigma ,{{S}_{c}},E,I,A,T} \right)d\varsigma } + \int\limits_0^t {{{H}_{2}}\left( {\varsigma ,E} \right)d{{\beta }_{2}}\left( \varsigma \right)} , \\ I\left( t \right) = I\left( 0 \right) + \int\limits_0^t {{{G}_{3}}\left( {\varsigma ,{{S}_{c}},E,I,A,T} \right)d\varsigma } + \int\limits_0^t {{{H}_{3}}\left( {\varsigma ,I} \right)d{{\beta }_{3}}\left( \varsigma \right)} , \\ A\left( t \right) = A\left( 0 \right) + \int\limits_0^t {{{G}_{4}}\left( {\varsigma ,{{S}_{c}},E,I,A,T} \right)d\varsigma } + \int\limits_0^t {{{H}_{4}}\left( {\varsigma ,A} \right)d{{\beta }_{4}}\left( \varsigma \right)} , \\ T\left( t \right) = T\left( 0 \right) + \int\limits_0^t {{{G}_{5}}\left( {\varsigma ,{{S}_{c}},E,I,A,T} \right)d\varsigma } + \int\limits_0^t {{{H}_{5}}\left( {\varsigma ,T} \right)d{{\beta }_{5}}\left( \varsigma \right)} . \\ \end{aligned} $$
(10)

To present our proof, we give state and apply the following theorem as in [11, 25].

Theorem 1. Assume that, there exist \({{\mathcal{K}}_{\iota }}\), \({{\tilde {\mathcal{K}}}_{\iota }}\) such that the following conditions:

(1) \({{\left| {{{G}_{\iota }}\left( {x,t} \right) - {{G}_{\iota }}\left( {{{x}_{\iota }},t} \right)} \right|}^{2}} < {{\mathcal{K}}_{\iota }}{{\left| {x - {{x}_{\iota }}} \right|}^{2}}\), \({{\left| {{{H}_{\iota }}\left( {x,t} \right) - {{H}_{\iota }}\left( {{{x}_{\iota }},t} \right)} \right|}^{2}} < {{\tilde {\mathcal{K}}}_{\iota }}{{\left| {x - {{x}_{\iota }}} \right|}^{2}}\),

(2) \(\forall \left( {x,t} \right) \in {{\mathbb{R}}^{5}} \times \left[ {0,T} \right]\), then

\({{\left| {{{G}_{\iota }}\left( {x,t} \right)} \right|}^{2}}\), \(~{{\left| {{{H}_{\iota }}\left( {x,t} \right)} \right|}^{2}} < \mathcal{K}({{\left| x \right|}^{2}} + 1)\),

are satisfied for \(i = 1,2, \ldots ,5\).

There exists a unique solution \(\mathfrak{D}\left( t \right) \in {{\mathbb{R}}^{5}}\) for Eq. (9) and it belongs to \({{\mathcal{M}}^{2}}\left( {\left[ {0,T} \right],{{\mathbb{R}}^{5}}} \right)\). The proof presented in the paper follows the approach used in [25] in proving the existence and uniqueness of solutions. We verify that the conditions (1) and (2) in Theorem 1 holds for our model. Firstly, we investigate the functions \({{G}_{1}}\left( {t,{{S}_{c}},E,I,A,T} \right)\) and \(H{{\_\{ 1\} }}(t,S{{\_}}c)\) for the susceptible population. We show the proof for the function \(G\) by using \(\left( {t,{{S}_{c}}} \right)\).

Proof. Let

$${{\left| {{{G}_{1}}\left( {t,{{S}_{c}}} \right) - {{G}_{1}}\left( {t,{{S}_{{c1}}}} \right)} \right|}^{2}} = {{\left| {\left( {\lambda + \mu } \right)\left( {{{S}_{c}} - {{S}_{{c1}}}} \right)} \right|}^{2}}.$$
(11)

The following norm,

$${{\left\| \Psi \right\|}_{\infty }} = \mathop {{\text{sup}}}\limits_{t \in \left[ {0,\mathcal{T}} \right]} {{\left| \Psi \right|}^{2}},$$

transforms (11) to

$$\begin{array}{*{20}{r}} \begin{aligned} {{\left| {{{G}_{1}}\left( {t,{{S}_{c}}} \right) - {{G}_{1}}\left( {t,{{S}_{{c1}}}} \right)} \right|}^{2}} \leqslant \mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} {{\left| {\left( {\lambda + \mu } \right)\left( {{{S}_{c}} - {{S}_{{c1}}}} \right)} \right|}^{2}}, \\ \leqslant \left\| {\left( {\lambda + \mu } \right)} \right\|_{\infty }^{2}{{\left| {{{S}_{c}} - {{S}_{{c1}}}} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}_{1}}{{\left| {{{S}_{c}} - {{S}_{{c1}}}} \right|}^{2}}, \\ \end{aligned} \end{array}$$

and

$$\begin{aligned} {{\left| {{{H}_{1}}\left( {{{S}_{c}},t} \right) - {{H}_{1}}\left( {{{S}_{{c1}}},t} \right)} \right|}^{2}} = {{\left| {\left( {{{\Lambda }_{{11}}}{{S}_{c}} + {{\Lambda }_{{12}}}} \right){{S}_{c}} - \left( {{{\Lambda }_{{11}}}{{S}_{{c1}}} + {{\Lambda }_{{12}}}} \right){{S}_{{c1}}}} \right|}^{2}}, \\ \leqslant {{\left| {({{\Lambda }_{{11}}}\left( {S_{c}^{2} - S_{{c1}}^{2}} \right) - {{\Lambda }_{{12}}}\left( {{{S}_{c}} - {{S}_{{c1}}}} \right)} \right|}^{2}}, \\ \leqslant {{\left( {{{\Lambda }_{{11}}}\left( {{{S}_{c}} + {{S}_{{c1}}}} \right) + {{\Lambda }_{{12}}}} \right)}^{2}}{{\left| {{{S}_{c}} - {{S}_{{c1}}}} \right|}^{2}}, \\ \leqslant \left( {\Lambda _{{11}}^{2}{{{({{S}_{c}} + {{S}_{{c1}}})}}^{2}} + 2{{\Lambda }_{{11}}}{{\Lambda }_{{12}}}\left( {{{S}_{c}} + {{S}_{{c1}}}} \right) + \Lambda _{{12}}^{2}} \right){{\left| {{{S}_{c}} - {{S}_{{c1}}}} \right|}^{2}}, \\ \leqslant \left( {\Lambda _{{11}}^{2}\left( {S_{c}^{2} + 2{{S}_{{c1}}} + S_{{c1}}^{2}} \right) + 2{{\Lambda }_{{11}}}{{\Lambda }_{{12}}}\left( {{{S}_{c}} + {{S}_{{c1}}}} \right) + \Lambda _{{12}}^{2}} \right){{\left| {{{S}_{c}} - {{S}_{{c1}}}} \right|}^{2}}, \\ \leqslant \left( {\mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left| {S_{c}^{2}\left( t \right)} \right| + 2\mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left| {{{S}_{c}}\left( t \right)} \right|\mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left| {{{S}_{{c1}}}\left( t \right)} \right|} \right. \\ + \mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left| {S_{{c1}}^{t}\left( t \right)} \right| + 2{{\Lambda }_{{11}}}{{\Lambda }_{{12}}}\left( {\mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left| {{{S}_{c}}\left( t \right)} \right|} \right. \\ \left. {\left. { + \;\mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left| {{{S}_{{c1}}}\left( t \right)} \right|} \right) + \Lambda _{{12}}^{2}} \right){{\left| {{{S}_{c}} - {{S}_{{c1}}}} \right|}^{2}} \\ \leqslant \left( {\Lambda _{{11}}^{2}} \right.\left( {{{{\left\| {S_{c}^{2}} \right\|}}_{\infty }} + 2{{{\left\| {{{S}_{c}}} \right\|}}_{\infty }}{{{\left\| {{{S}_{{c1}}}} \right\|}}_{\infty }} + {{{\left\| {S_{{c1}}^{2}} \right\|}}_{\infty }}} \right) \\ \left. { + \;2{{\Lambda }_{{11}}}{{\Lambda }_{{12}}}{{{\left\| {{{S}_{c}}} \right\|}}_{\infty }}{{{\left\| {{{S}_{{c1}}}} \right\|}}_{\infty }} + \Lambda _{{12}}^{2}} \right){{\left| {{{S}_{c}} - {{S}_{{c1}}}} \right|}^{2}} \\ \leqslant {{{\tilde {\mathcal{K}}}}_{1}}{{\left| {{{S}_{c}} - {{S}_{{c1}}}} \right|}^{2}}, \\ \end{aligned} $$
(12)

in which

$$\begin{aligned} {{{\tilde {\mathcal{K}}}}_{1}} = \Lambda _{{11}}^{2}\left( {{{{\left\| {S_{c}^{2}} \right\|}}_{\infty }} + 2{{{\left\| {{{S}_{c}}} \right\|}}_{\infty }}{{{\left\| {{{S}_{{c1}}}} \right\|}}_{\infty }} + {{{\left\| {S_{{c1}}^{2}} \right\|}}_{\infty }}} \right) + 2{{\Lambda }_{{11}}}{{\Lambda }_{{12}}}{{\left\| {{{S}_{c}}} \right\|}_{\infty }}{{\left\| {{{S}_{{c1}}}} \right\|}_{\infty }} + \Lambda _{{12}}^{2} \\ = \Lambda _{{11}}^{2}{{\left( {{{{\left\| {{{S}_{c}}} \right\|}}_{\infty }} + \left. {{{{\left\| {{{S}_{{c1}}}} \right\|}}_{\infty }}} \right\|} \right)}^{2}} + \left. {2{{\Lambda }_{{11}}}{{\Lambda }_{{12}}}{{{\left\| {{{S}_{c}}} \right\|}}_{\infty }}{{{\left\| {{{S}_{{c1}}}} \right\|}}_{\infty }}} \right\| + \Lambda _{{12}}^{2}. \\ \end{aligned} $$

In a similar manner, we can show that the remaining equations of model (8) satisfies condition (1) of Theorem 1. Thus,

$$\begin{aligned} {{{\tilde {\mathcal{K}}}}_{2}} = \Lambda _{{21}}^{2}{{\left( {{{{\left\| E \right\|}}_{\infty }} + \left. {{{{\left\| {{{E}_{1}}} \right\|}}_{\infty }}} \right\|} \right)}^{2}} + 2{{\Lambda }_{{21}}}{{\Lambda }_{{22}}}{{\left\| E \right\|}_{\infty }}{{\left\| {{{E}_{1}}} \right\|}_{\infty }} + \Lambda _{{22}}^{2}, \\ {{{\tilde {\mathcal{K}}}}_{3}} = \Lambda _{{31}}^{2}{{\left( {{{{\left\| I \right\|}}_{\infty }} + \left. {{{{\left\| {{{I}_{1}}} \right\|}}_{\infty }}} \right\|} \right)}^{2}} + 2{{\Lambda }_{{31}}}{{\Lambda }_{{32}}}{{\left\| I \right\|}_{\infty }}{{\left\| {{{I}_{1}}} \right\|}_{\infty }} + \Lambda _{{32}}^{2}, \\ {{{\tilde {\mathcal{K}}}}_{4}} = \Lambda _{{41}}^{2}{{\left( {{{{\left\| A \right\|}}_{\infty }} + \left. {{{{\left\| {{{A}_{1}}} \right\|}}_{\infty }}} \right\|} \right)}^{2}} + 2{{\Lambda }_{{41}}}{{\Lambda }_{{42}}}{{\left\| A \right\|}_{\infty }}{{\left\| {{{A}_{1}}} \right\|}_{\infty }} + \Lambda _{{42}}^{2}, \\ {{{\tilde {\mathcal{K}}}}_{5}} = \Lambda _{{51}}^{2}{{\left( {{{{\left\| T \right\|}}_{\infty }} + \left. {{{{\left\| {{{T}_{1}}} \right\|}}_{\infty }}} \right\|} \right)}^{2}} + 2{{\Lambda }_{{51}}}{{\Lambda }_{{52}}}{{\left\| T \right\|}_{\infty }}{{\left\| {{{T}_{1}}} \right\|}_{\infty }} + \Lambda _{{52}}^{2}. \\ \end{aligned} $$

Further, we consider the \(E\) class and obtain

$$\begin{aligned} {{\left| {{{G}_{2}}\left( {E,t} \right) - {{G}_{2}}\left( {{{E}_{1}},t} \right)} \right|}^{2}} = {{\left| { - {{Q}_{1}}\left( {E - {{E}_{1}}} \right)} \right|}^{2}}, \\ \leqslant 2{{\left| {{{Q}_{1}}} \right|}^{2}}{{\left| {E - {{E}_{1}}} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}_{2}}{{\left| {E - {{E}_{1}}} \right|}^{2}}, \\ \end{aligned} $$

where \({{\mathcal{K}}_{2}} = 2{{\left| {{{Q}_{1}}} \right|}^{2}}\).

Also, for the \(I\) class we have that

$$\begin{aligned} {{\left| {{{G}_{3}}\left( {I,t} \right) - {{G}_{3}}\left( {{{I}_{1}},t} \right)} \right|}^{2}} = {{\left| { - {{Q}_{2}}\left( {I - {{I}_{1}}} \right)} \right|}^{2}}, \\ \leqslant 2{{\left| {{{Q}_{2}}} \right|}^{2}}{{\left| {I - {{I}_{1}}} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}_{3}}{{\left| {I - {{I}_{1}}} \right|}^{2}}, \\ \end{aligned} $$

where \({{\mathcal{K}}_{3}} = 2{{\left| {{{Q}_{2}}} \right|}^{2}}\). Similarly, we have that

$$\begin{aligned} {{\left| {{{G}_{5}}\left( {A,t} \right) - {{G}_{5}}\left( {{{A}_{1}},t} \right)} \right|}^{2}} = {{\left| { - \mu \left( {A - {{A}_{1}}} \right)} \right|}^{2}}, \\ \leqslant 2{{\left| \mu \right|}^{2}}{{\left| {A - {{A}_{1}}} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}_{4}}{{\left| {A - {{A}_{1}}} \right|}^{2}} \\ \end{aligned} $$

and

$$\begin{aligned} {{\left| {{{G}_{5}}\left( {T,t} \right) - {{G}_{5}}\left( {{{T}_{1}},t} \right)} \right|}^{2}} = {{\left| { - {{Q}_{3}}\left( {T - {{T}_{1}}} \right)} \right|}^{2}}, \\ \leqslant 2{{\left| {{{Q}_{3}}} \right|}^{2}}{{\left| {T - {{T}_{1}}} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}_{5}}{{\left| {T - {{t}_{1}}} \right|}^{2}}, \\ \end{aligned} $$

where \({{\mathcal{K}}_{4}} = 2{{\left| \mu \right|}^{2}}\) and \({{\mathcal{K}}_{5}} = 2{{\left| {{{Q}_{3}}} \right|}^{2}}\), respectively.

Next, we verify that conditions (2) hold for our model (9)

$$\begin{aligned} {{\left| {{{G}_{1}}\left( {{{S}_{c}},t} \right)} \right|}^{2}} = {{\left| {\pi - \left( {\lambda + \mu } \right){{S}_{c}}} \right|}^{2}}, \\ \leqslant {{\left| {\pi {{S}_{c}} - \left( {\lambda + \mu } \right){{S}_{c}}} \right|}^{2}}, \\ \leqslant {{\left| {{{S}_{c}}} \right|}^{2}}{{\left| {\pi - \left( {\lambda + \mu } \right)} \right|}^{2}}, \\ \leqslant \left( {{{{\left| {{{S}_{c}}} \right|}}^{2}} + 1} \right){{\left| {\pi - \left( {\lambda + \mu } \right)} \right|}^{2}}, \\ \leqslant \left( {{{{\left| {{{S}_{c}}} \right|}}^{2}} + 1} \right)\mathop {{\text{sup}}}\limits_{t \in \left[ {0,\mathcal{T}} \right]} {{\left| {\pi - \left( {\lambda + \mu } \right)} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}^{1}}\left( {{{{\left| {{{S}_{c}}} \right|}}^{2}} + 1} \right), \\ \end{aligned} $$
$${{\mathcal{K}}^{1}} = \mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} {{\left| {\pi - \left( {\lambda + \mu } \right)} \right|}^{2}}.$$

Also,

$$\begin{aligned} {{\left| {{{H}_{1}}\left( {{{S}_{c}},t} \right) - {{H}_{1}}\left( {{{S}_{{c1}}},t} \right)} \right|}^{2}} = {{\left| {\left( {{{{{\Lambda }}}_{{11}}}{{S}_{c}} + {{{{\Lambda }}}_{{12}}}} \right){{S}_{c}}} \right|}^{2}}, \\ \leqslant {{\left| {{{{{\Lambda }}}_{{11}}}S_{c}^{2} + {{{{\Lambda }}}_{{12}}}S_{c}^{2}} \right|}^{2}}, \\ \leqslant {{({{{{\Lambda }}}_{{11}}} + {{{{\Lambda }}}_{{12}}})}^{2}}{{\left| {S_{c}^{2}} \right|}^{2}}, \\ \leqslant {{({{{{\Lambda }}}_{{11}}} + {{{{\Lambda }}}_{{12}}})}^{2}}\mathop {{\text{sup}}}\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left| {S_{c}^{2}} \right|{{\left| {{{S}_{c}}} \right|}^{2}}, \\ \leqslant {{({{{{\Lambda }}}_{{11}}} + {{{{\Lambda }}}_{{12}}})}^{2}}{{\left\| {S_{c}^{2}} \right\|}_{\infty }}\left( {{{{\left| {{{S}_{c}}} \right|}}^{2}} + 1} \right), \\ \leqslant {{{\tilde {\mathcal{K}}}}^{1}}\left( {{{{\left| {{{S}_{c}}} \right|}}^{2}} + 1} \right), \\ \end{aligned} $$
(13)

in which

$${{\tilde {\mathcal{K}}}^{1}} = {{({{{{\Lambda }}}_{{11}}} + {{{{\Lambda }}}_{{12}}})}^{2}}{{\left\| {S_{c}^{2}} \right\|}_{\infty }}.$$

In similar fashion

$$\begin{aligned} {{{\tilde {\mathcal{K}}}}^{2}} = {{({{{{\Lambda }}}_{{21}}} + {{{{\Lambda }}}_{{22}}})}^{2}}{{\left\| {{{E}^{2}}} \right\|}_{\infty }}, \\ {{{\tilde {\mathcal{K}}}}^{3}} = {{({{{{\Lambda }}}_{{31}}} + {{{{\Lambda }}}_{{32}}})}^{2}}{{\left\| {{{I}^{2}}} \right\|}_{\infty }}, \\ {{{\tilde {\mathcal{K}}}}^{4}} = {{({{{{\Lambda }}}_{{41}}} + {{{{\Lambda }}}_{{42}}})}^{2}}{{\left\| {{{A}^{2}}} \right\|}_{\infty }}, \\ {{{\tilde {\mathcal{K}}}}^{5}} = {{({{{{\Lambda }}}_{{51}}} + {{{{\Lambda }}}_{{52}}})}^{2}}{{\left\| {{{T}^{2}}} \right\|}_{\infty }}. \\ \end{aligned} $$

Also, for the \(E,I,A\), and \(T\) classes, we have that

$$\begin{aligned} {{\left| {{{H}_{2}}\left( {E,t} \right)} \right|}^{2}} = {{\left| {\lambda {{S}_{c}} - {{Q}_{1}}E} \right|}^{2}}, \\ \leqslant {{\left| {\lambda {{S}_{c}} - {{Q}_{1}}} \right|}^{2}}{{\left| E \right|}^{2}}, \\ \leqslant \left( {{{{\left| E \right|}}^{2}} + 1} \right)\mathop {\sup }\limits_{t \in \left[ {0,\mathcal{T}} \right]} {{\left| {\lambda {{S}_{c}} - {{Q}_{1}}} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}^{2}}\left( {{{{\left| E \right|}}^{2}} + 1} \right), \\ \end{aligned} $$
$$\begin{aligned} {{\left| {{{H}_{3}}\left( {I,t} \right)} \right|}^{2}} = {{\left| {\sigma \rho E - {{Q}_{2}}I} \right|}^{2}}, \\ \leqslant {{\left| {\sigma \rho E - {{Q}_{2}}} \right|}^{2}}{{\left| I \right|}^{2}}, \\ \leqslant \left( {{{{\left| I \right|}}^{2}} + 1} \right)\mathop {{\text{sup}}}\limits_{t \in \left[ {0,\mathcal{T}} \right]} {{\left| {\sigma \rho E - {{Q}_{2}}} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}^{3}}\left( {{{{\left| I \right|}}^{2}} + 1} \right), \\ \end{aligned} $$
$$\begin{aligned} {{\left| {{{H}_{4}}\left( {A,t} \right)} \right|}^{2}} = {{\left| {\sigma \left( {1 - \rho } \right)E - \mu A} \right|}^{2}}, \\ \leqslant {{\left\| {\sigma \left( {1 - \rho } \right)E - \left. \mu \right\|} \right.}^{2}}{{\left| A \right|}^{2}}, \\ \leqslant \left( {{{{\left| A \right|}}^{2}} + 1} \right)\mathop {{\text{sup}}}\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left\| {\sigma \left( {1 - \rho } \right)E} \right. - {{\left. \mu \right|}^{2}}, \\ \leqslant {{\mathcal{K}}^{4}}\left( {{\text{|}}A{{|}^{2}} + 1} \right) \\ \end{aligned} $$

and

$$\begin{aligned} {{\left| {{{H}_{5}}\left( {T,t} \right)} \right|}^{2}} = {{\left| {{{\nu }_{1}}I - {{Q}_{3}}T} \right|}^{2}}, \\ \leqslant \left\| {{{\nu }_{1}}I} \right. - {{\left. {{{Q}_{3}}} \right|}^{2}}{{\left| T \right|}^{2}}, \\ \leqslant \left( {{{{\left| T \right|}}^{2}} + 1} \right)\mathop {{\text{sup}}}\limits_{t \in \left[ {0,\mathcal{T}} \right]} \left\| {{{\nu }_{1}}I} \right. - {{\left. {{{Q}_{3}}} \right|}^{2}}, \\ \leqslant {{\mathcal{K}}^{5}}\left( {{{{\left| T \right|}}^{2}} + 1} \right), \\ \end{aligned} $$

where \({{\tilde {\mathcal{K}}}^{2}} = {{\sup }_{{t \in \left[ {0,\mathcal{T}} \right]}}}\left\| {{{\nu }_{1}}I} \right. - {{\left. {{{Q}_{3}}} \right|}^{2}}\), \({{\tilde {\mathcal{K}}}^{3}} = {{\sup }_{{t \in \left[ {0,\mathcal{T}} \right]}}}{{\left| {\sigma \rho E - {{Q}_{2}}} \right|}^{2}}\), \({{\tilde {\mathcal{K}}}^{4}} = {{\sup }_{{t \in \left[ {0,\mathcal{T}} \right]}}}\left\| {\sigma \left( {1 - \rho } \right)E} \right. - {{\left. \mu \right|}^{2}}\) and \({{\tilde {\mathcal{K}}}^{5}}\) = \({\text{su}}{{{\text{p}}}_{{t \in \left[ {0,\mathcal{T}} \right]}}}\left\| {{{\nu }_{1}}I} \right. - {{\left. {{{Q}_{3}}} \right|}^{2}}\).

Since both \({{G}_{\iota }}\) and \({{H}_{\iota }}\) for \(i = 1,2, \ldots ,5\) satisfies all the conditions given in Theorem 1 thus model (9) exists and have a unique solution. This completes the proof.

4.2 Application of the Schemes to the Model

In this subsection, we apply the suggested numerical schemes to solve our model. Using the CF fractional derivative,

$$\begin{array}{*{20}{l}} {~_{0}^{{CF}}D_{t}^{\chi }{{S}_{c}}}&{~ = }&{\pi - \beta \left( {I{\kern 1pt} ^* + \;{{\theta }_{1}}T{\kern 1pt} ^* + \;{{\theta }_{2}}A + \mu } \right){{S}_{c}},} \\ {~_{0}^{{CF}}D_{t}^{\chi }E}&{~ = }&{\beta \left( {I{\kern 1pt} ^* + \;{{\theta }_{1}}T{\kern 1pt} ^* + \;{{\theta }_{2}}A + \mu } \right){{S}_{c}} - {{Q}_{1}}E,} \\ {~_{0}^{{CF}}D_{t}^{\chi }I}&{~ = }&{\sigma \rho E - {{Q}_{2}}I,} \\ {~_{0}^{{CF}}D_{t}^{\chi }A}&{~ = }&{\sigma \left( {1 - \rho } \right)E - \mu A,} \\ {~_{0}^{{CF}}D_{t}^{\chi }T}&{~ = }&{{{\nu }_{1}}I - {{Q}_{3}}T.} \end{array}$$

To reduce complexity, we rewrite the model equations as follows.

$$\begin{aligned} ~_{0}^{{CF}}D_{t}^{\chi }{{S}_{c}} = S_{c}^{*}\left( {t,{{S}_{c}},E,I,A,T} \right), \\ ~_{0}^{{CF}}D_{t}^{\chi }E = E{\kern 1pt} ^*{\kern 1pt} \left( {t,{{S}_{c}},E,I,A,T} \right), \\ ~_{0}^{{CF}}D_{t}^{\chi }I = I{\kern 1pt} ^*{\kern 1pt} \left( {t,{{S}_{c}},E,I,A,T} \right), \\ ~_{0}^{{CF}}D_{t}^{\chi }A = A{\kern 1pt} ^*{\kern 1pt} \left( {t,{{S}_{c}},E,I,A,T} \right), \\ ~_{0}^{{CF}}D_{t}^{\chi }T = T{\kern 1pt} ^*{\kern 1pt} \left( {t,{{S}_{c}},E,I,A,T} \right). \\ \end{aligned} $$

Thus,

$$S_{c}^{{k + 1}}~ = \frac{{1 - \chi }}{{M\left( \chi \right)}}\left[ {S_{c}^{*}\left( {{{t}_{{k + 1}}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)} \right.$$
$$\left. { - \;S_{c}^{*}\left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)} \right] + \frac{\chi }{{M\left( \chi \right)}}\left[ {\frac{{23}}{{12}}S_{c}^{*}\left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)\Delta t} \right.$$
$$ - \;\frac{4}{3}S_{c}^{*}\left( {{{t}_{k}},S_{c}^{k} + {{\Delta }}tS_{c}^{{k{\text{*}}}},{{E}^{n}} - {{\Delta }}t{{E}^{{k{\text{*}}}}},{{I}^{k}} - {{\Delta }}t{{I}^{{k{\text{*}}}}},{{A}^{k}} - {{\Delta }}t{{A}^{{k{\text{*}}}}},{{T}^{k}} - {{\Delta }}t{{T}^{{k{\text{*}}}}}} \right){{\Delta }}t$$
$$ + \;\frac{{15}}{{12}}S_{c}^{{\text{*}}}\left( {{{t}_{{k - 2}}},{{S}^{k}} - {{\Delta }}tS_{c}^{{k{\text{*}}}} - {{\Delta }}tS_{c}^{{\left( {k - 1} \right){\text{*}}}},{{E}^{k}} - {{\Delta }}t{{E}^{{k{\text{*}}}}} - {{\Delta }}t{{E}^{{\left( {k - 1} \right){\text{*}}}}}{{I}^{k}} - {{\Delta }}t{{I}^{{k{\text{*}}}}}} \right.$$
$$\left. {\left. { - \;{{\Delta }}t{{I}^{{\left( {k - 1} \right){\text{*}}}}}{{A}^{k}} - {{\Delta }}t{{A}^{{k{\text{*}}}}} - {{\Delta }}t{{A}^{{\left( {k - 1} \right){\text{*}}}}}{{T}^{k}} - {{\Delta }}t{{T}^{{k{\text{*}}}}} - {{\Delta }}tt{{T}^{{\left( {k - 1} \right){\text{*}}}}}} \right){{\Delta }}t} \right],$$
$${{E}^{{k + 1}}}~ = \frac{{1 - \chi }}{{M\left( \chi \right)}}\left[ {E{\text{*}}\left( {{{t}_{{k + 1}}},S_{c}^{k} + {{\Delta }}tS_{c}^{{k{\text{*}}}},{{E}^{k}} + {{\Delta }}t{{E}^{{k{\text{*}}}}},{{I}^{k}} + {{\Delta }}t{{I}^{{k{\text{*}}}}},{{A}^{k}} + {{\Delta }}t{{A}^{{k{\text{*}}}}},{{T}^{k}} + {{\Delta }}t{{T}^{{k{\text{*}}}}}} \right)} \right.$$
$$~\left. {^{{^{{}}}} - \;E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)} \right] + \frac{\chi }{{M\left( \chi \right)}}\left[ {\frac{{23}}{{12}}E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)\Delta t} \right.$$
$$ - \;\frac{4}{3}E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} - \Delta t{{E}^{{k^*}}},{{I}^{k}} - \Delta t{{I}^{{k^*}}},{{A}^{k}} - \Delta t{{A}^{{k^*}}},{{T}^{k}} - \Delta t{{T}^{{k^*}}}} \right)\Delta t$$
$$ + \;\frac{{15}}{{12}}E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k - 2}}},S_{c}^{k} - \Delta tS_{c}^{{k^*}} - \Delta tS_{c}^{{\left( {k - 1} \right)^*}},{{E}^{k}} - \Delta t{{E}^{{k^*}}} - \Delta t{{E}^{{\left( {k - 1} \right)^*}}}{{I}^{k}} - \Delta t{{I}^{{k^*}}}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\left( {k - 1} \right)^*}}}{{A}^{k}} - \Delta t{{A}^{{k^*}}} - \Delta t{{A}^{{\left( {k - 1} \right)^*}}}{{T}^{k}} - \Delta t{{T}^{{k^*}}} - \Delta tt{{T}^{{\left( {k - 1} \right)^*}}}} \right)\Delta t} \right],$$
$${{I}^{{k + 1}}} = \frac{{1 - \chi }}{{M\left( \chi \right)}}\left[ {I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k + 1}}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)} \right.$$
$$\left. {^{{^{{}}}} - \;I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)} \right] + \frac{\chi }{{M\left( \chi \right)}}\left[ {\frac{{23}}{{12}}I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)\Delta t} \right.$$
$$ - \;\frac{4}{3}I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} - \Delta t{{E}^{{k^*}}},{{I}^{k}} - \Delta t{{I}^{{k^*}}},{{A}^{k}} - \Delta t{{A}^{{k^*}}},{{T}^{k}} - \Delta t{{T}^{{k^*}}}} \right)\Delta t$$
$$ + \;\frac{{15}}{{12}}I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k - 2}}},S_{c}^{k} - \Delta tS_{c}^{{k^*}} - \Delta tS_{c}^{{\left( {k - 1} \right)^*}},{{E}^{k}} - \Delta t{{E}^{{k^*}}} - \Delta t{{E}^{{\left( {k - 1} \right)^*}}}{{I}^{k}} - \Delta t{{I}^{{k^*}}}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\left( {k - 1} \right)^*}}}{{A}^{k}} - \Delta t{{A}^{{k^*}}} - \Delta t{{A}^{{\left( {k - 1} \right)^*}}}{{T}^{k}} - \Delta t{{T}^{{k^*}}} - \Delta tt{{T}^{{\left( {k - 1} \right)^*}}}} \right)\Delta t} \right],$$
$${{A}^{{k + 1}}} = \frac{{1 - \chi }}{{M\left( \chi \right)}}\left[ {A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k + 1}}},{{S}^{k}} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)} \right.$$
$$\left. {^{{^{{}}}} - \;A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)} \right] + \frac{\chi }{{M\left( \chi \right)}}\left[ {\frac{{23}}{{12}}A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)\Delta t} \right.$$
$$ - \;\frac{4}{3}A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} - \Delta t{{E}^{{k^*}}},{{I}^{k}} - \Delta t{{I}^{{k^*}}},{{A}^{k}} - \Delta t{{A}^{{k^*}}},{{T}^{k}} - \Delta t{{T}^{{k^*}}}} \right)\Delta t$$
$$ + \;\frac{{15}}{{12}}A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k - 2}}},{{S}^{k}} - \Delta tS_{c}^{{k^*}} - \Delta tS_{c}^{{\left( {k - 1} \right)^*}},{{E}^{k}} - \Delta t{{E}^{{k^*}}} - \Delta t{{E}^{{\left( {k - 1} \right)^*}}}{{I}^{k}} - \Delta t{{I}^{{k^*}}}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\left( {k - 1} \right)^*}}}{{A}^{k}} - \Delta t{{A}^{{k^*}}} - \Delta t{{A}^{{\left( {k - 1} \right)^*}}}{{T}^{k}} - \Delta t{{T}^{{k^*}}} - \Delta tt{{T}^{{\left( {k - 1} \right)^*}}}} \right)\Delta t} \right],$$
$${{T}^{{k + 1}}}~ = \frac{{1 - \chi }}{{M\left( \chi \right)}}\left[ {T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k + 1}}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)} \right.$$
$$\left. {^{{^{{}}}} - \;T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)} \right] + \frac{\chi }{{M\left( \chi \right)}}\left[ {\frac{{23}}{{12}}T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k},{{E}^{k}},{{I}^{k}},{{A}^{k}},{{T}^{k}}} \right)\Delta t} \right.$$
$$ - \;\frac{4}{3}T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{k}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} - \Delta t{{E}^{{k^*}}},{{I}^{k}} - \Delta t{{I}^{{k^*}}},{{A}^{k}} - \Delta t{{A}^{{k^*}}},{{T}^{k}} - \Delta t{{T}^{{k^*}}}} \right)\Delta t$$
$$ + \;\frac{{15}}{{12}}T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k - 2}}},S_{c}^{k} - \Delta tS_{c}^{{k^*}} - \Delta tS_{c}^{{\left( {k - 1} \right)^*}},{{E}^{k}} - \Delta t{{E}^{{k^*}}} - \Delta t{{E}^{{\left( {k - 1} \right)^*}}}{{I}^{k}} - \Delta t{{I}^{{k^*}}}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\left( {k - 1} \right)^*}}}{{A}^{k}} - \Delta t{{A}^{{k^*}}} - \Delta t{{A}^{{\left( {k - 1} \right)^*}}}{{T}^{k}} - \Delta t{{T}^{{k^*}}} - \Delta tt{{T}^{{\left( {k - 1} \right)^*}}}} \right)\Delta t} \right].$$

The ABC numerical solution of the model is:

$$S_{c}^{{k + 1}}~ = \frac{{1 - \chi }}{{AB\left( \chi \right)}}S_{c}^{*}\left( {{{t}_{{k + 1}}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 1} \right)}}\mathop \sum \limits_{\iota = 2}^k \,\left[ {S_{c}^{*}\left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }}} \right.} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\prod ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 2} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {S_{c}^{*}\left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}}{{T}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{T}^{{\iota *}}}} \right) - S_{c}^{*}\left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\sum ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{2AB\left( \chi \right)\varphi \left( {\chi + 3} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {S_{c}^{*}\left( {{{t}_{i}},S_{c}^{\iota },{{E}^{\iota }},{{I}^{\iota }},{{A}^{\iota }},{{T}^{\iota }}} \right) - 2S_{c}^{*}\left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{E}^{{\iota *}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}}} \right) + S_{c}^{*}\left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }}} \right.$$
$$ - \;\Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }}$$
$$\left. {\left. { - \;\Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\Delta ,$$
$${{E}^{{k + 1}}} = \frac{{1 - \chi }}{{AB\left( \chi \right)}}E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k + 1}}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 1} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }}} \right.} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\prod ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 2} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}}{{T}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{T}^{{\iota *}}}} \right) - E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\sum ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{2AB\left( \chi \right)\varphi \left( {\chi + 3} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{i}},S_{c}^{\iota },{{E}^{\iota }},{{I}^{\iota }},{{A}^{\iota }},{{T}^{\iota }}} \right) - 2E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{E}^{{\iota *}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}}} \right) + E{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }}} \right.$$
$$ - \;\Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }}$$
$$\left. {\left. { - \;\Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\Delta ,$$
$${{I}^{{k + 1}}} = \frac{{1 - \chi }}{{AB\left( \chi \right)}}I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k + 1}}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 1} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {I{\kern 1pt} ^*{\kern 1pt} ({{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\prod ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 2} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}}{{T}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{T}^{{\iota *}}}} \right) - I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\sum ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{2AB\left( \chi \right)\varphi \left( {\chi + 3} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{i}},S_{c}^{\iota },{{E}^{\iota }},{{I}^{\iota }},{{A}^{\iota }},{{T}^{\iota }}} \right) - 2I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{E}^{{\iota *}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}}} \right) + I{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }}} \right.$$
$$ - \;\Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }}$$
$$\left. {\left. { - \;\Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\Delta ,$$
$${{A}^{{k + 1}}} = \frac{{1 - \chi }}{{AB\left( \chi \right)}}A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k + 1}}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 1} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }}} \right.} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\prod ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 2} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}}{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}}{{T}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{T}^{{\iota *}}}} \right) - A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}}{{I}^{\iota }}} \right.$$
$$ - \;\left. {\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}}{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}}{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}})} \right]\sum ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{2AB\left( \chi \right)\varphi \left( {\chi + 3} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{i}},S_{c}^{\iota },{{E}^{\iota }},{{I}^{\iota }},{{A}^{\iota }},{{T}^{\iota }}} \right) - 2A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{E}^{{\iota *}}},{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}},{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}},{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}}} \right) + A{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }}} \right.$$
$$ - \;\Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}},{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}},{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}},{{T}^{\iota }}$$
$$\left. {\left. { - \;\Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\Delta ,$$
$${{T}^{{k + 1}}} = \frac{{1 - \chi }}{{AB\left( \chi \right)}}T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{k + 1}}},S_{c}^{k} + \Delta tS_{c}^{{k^*}},{{E}^{k}} + \Delta t{{E}^{{k^*}}},{{I}^{k}} + \Delta t{{I}^{{k^*}}},{{A}^{k}} + \Delta t{{A}^{{k^*}}},{{T}^{k}} + \Delta t{{T}^{{k^*}}}} \right)$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 1} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}},{{I}^{\iota }}} \right.} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}},{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}},{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\prod ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{AB\left( \chi \right)\varphi \left( {\chi + 2} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}},{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}},{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}},{{T}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{T}^{{\iota *}}}} \right) - T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }} - \Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}},{{I}^{\iota }}} \right.$$
$$\left. {\left. { - \;\Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}},{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}},{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}} - \Delta tt{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\sum ~$$
$$ + \;\frac{{\chi {{{(\Delta t)}}^{\chi }}}}{{2AB\left( \chi \right)\varphi \left( {\chi + 3} \right)}}\mathop \sum \limits_{\iota = 2}^k \left[ {T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{i}},S_{c}^{\iota },{{E}^{\iota }},{{I}^{\iota }},{{A}^{\iota }},{{T}^{\iota }}} \right) - 2T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 1}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}},{{E}^{\iota }}} \right.} \right.$$
$$\left. { - \;\Delta t{{E}^{{\iota *}}},{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}},{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}},{{T}^{\iota }} - \Delta t{{T}^{{\iota *}}}} \right) + T{\kern 1pt} ^*{\kern 1pt} \left( {{{t}_{{\iota - 2}}},S_{c}^{\iota } - \Delta tS_{c}^{{\iota *}} - \Delta tS_{c}^{{\left( {\iota - 1} \right)^*}},{{E}^{\iota }}} \right.$$
$$ - \;\Delta t{{E}^{{\iota *}}} - \Delta t{{E}^{{\left( {\iota - 1} \right)^*}}},{{I}^{\iota }} - \Delta t{{I}^{{\iota *}}} - \Delta t{{I}^{{\left( {\iota - 1} \right)^*}}},{{A}^{\iota }} - \Delta t{{A}^{{\iota *}}} - \Delta t{{A}^{{\left( {\iota - 1} \right)^*}}},{{T}^{\iota }}$$
$$\left. {\left. { - \;\Delta t{{T}^{{\iota *}}} - \Delta t{{T}^{{\left( {\iota - 1} \right)^*}}}} \right)} \right]\Delta {\kern 1pt} {\kern 1pt} .$$

5 NUMERICAL SIMULATION

The numerical scheme employed here is based on the recently developed Atangana–Seda scheme [11]. We obtain the numerical simulation results for both the power-law and Mittag–Leffler functions. The step size and the time interval considered in this work are 10−3 and [0, 20], respectively. The estimated parameter values used is given in Table 2.

Table 2. Parameter values used for numerical simulations
Full size table

5.1 Numerical Simulation Using Caputo Operator

Figure 2 gives the simulation results for the model based on Atanagana–Seda (2021) stochastic Mittag–Leffler numerical scheme. Figure 2a represents the number susceptible humans Sc(t). The number of individuals in this class decrease as the fractional derivative order increase from 0.75 to 1. The dynamics of the exposed class E(t) given in Fig. 2b shows an increase in the number of individuals as the fractional order increases and further the number of exposed individuals begin to decrease as the fractional derivative increase. Figure 2c, represents the symptomatic and infectious class I(t), the number of individuals reduce as the fractional order rises from 0.75 to 1. Figure 2d depicts the changes in infectious but asymptomatic class A(t). We observe that the number of individuals in A(t) increases as the fractional order increases. In Fig. 2e, the number of treated individuals T(t) decrease as the fractional order increases.

Fig. 2.
figure 2

Simulations for fractional stochastic COVID-19 model (9) via Mittag–Leffler function at α = 1, 0.9, 0.85, 0.75.

Full size image

5.2 Numerical Simulation Caputo Fabrizio Operator

Figure 3 is the numerical simulation results based on some selected fractional stochastic order. Figure 3a shows a decrease in the number of susceptible individuals Sc(t) as the fractional order increases. In Fig. 3b, the random effect is highly noticed and the number of individuals in the exposed class E(t) increase for a short time and after 6 days, the number of individuals begin to reduce as the fractional order increases from 0.75 to 1. In Fig. 3c we observe a decrease the number of infectious individuals I(t) as the fractional order increases from 0.75 to 1. In Fig. 3d, the random effect is pronounced and the number of individuals in the infectious but asymptomatic class A(t) increase as the fractional order increases. The simulation results for the treatment class T(t) is shown in Fig. 3e, where the number of individuals getting treated decrease as the fractional order increases toward the classical part.

Fig. 3.
figure 3

Simulations for fractional stochastic COVID-19 model (9) via exponential decay law at α = 1, 0.9, 0.85, 0.75.

Full size image

5.3 Numerical Simulation Using ABC Operator

Figure 4 is the numerical simulation results based on the recent, stochastic numerical scheme developed by Atangana and Seda [11] with power law. In Fig. 4a the number of susceptible humans Sc(t) decreases with time. This is expected, because, as more people get infected in the community, the virgin population will naturally reduce. In this situation, as the fractional order α increases from 0.75 to 1, the number of susceptible individuals decreases. Figure 4b shows that the number of exposed E(t) begins to increase with an increase in the fractional order. However, after some time, symptoms begin to manifest, and more of the individuals in the class E(t) then move to the infectious class. As a result, the number of exposed starts decreasing as the fractional order increases. Figure 4c shows the dynamics of the symptomatic and infectious class I(t). Here, the number of infectious humans decreases as the fractional order increases. In Fig. 4d, the population of the infectious but asymptomatic class A(t) increases as the fractional order increases. The dynamics of the treatment class T(t) are given in Fig. 4e which shows a decrease in the number of individuals treated as the fractional order increases.

Fig. 4.
figure 4

Simulations for fractional stochastic COVID-19 model (9) via power law at α = 1, 0.9, 0.85, 0.75.

Full size image

5.4 Model Fitting and Prediction of Future Number of New Cases and Deaths Using ACF

In this subsection, we use the seasonal autoregressive integrated moving average (SARIMA) method for time series forecasting with univariate data containing trends and seasonality [26]. The data used is the COVID-19 data for South Africa from March 2020 to July 2021. SARIMA is an extended version of autoregressive integrated moving average (ARIMA), which unlike ARIMA, supports data with seasonality and trends. It has three more frame works, which spell out the auto regression (AR), the number of times data series has to be differenced (I) and the moving average (MA) for the periodic component of the series, and another parameter for the interval of the seasonality. We employ the partial autocorrelation (PACF) and autocorrelation (ACF) to obtain parameters for the AR model and the MA model, respectively. Figures 5 and 6 represents graphs of autocorrelation functions for the infected and deaths in South Africa.

Fig. 5.
figure 5

Data fitting for South Africa COVID-19 cases and SARIMA prediction and forecasting.

Full size image
Fig. 6.
figure 6

Data fitting for South Africa COVID-19 cases and SARIMA prediction and forecasting.

Full size image

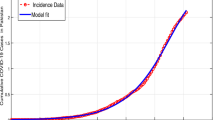
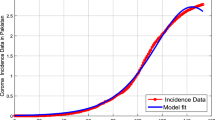
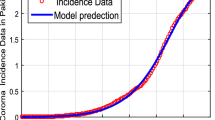
Next we fit the SARIMA model to COVID-19 South Africa data by first identifying the composition of the SARIMA (p,d,q)(P,D,Q), secondly, we approximate unspecified parameters, then, perform goodnessfit tests on the estimated residuals and finally we predict future outcomes based on the known data. The results from these processes are given in Figs. 7 and 8.

Fig. 7.
figure 7

Data fitting for South Africa COVID-19 cases and SARIMA prediction and forecasting.

Full size image
Fig. 8.
figure 8

Data fitting for South Africa COVID-19 cases and SARIMA prediction and forecasting.

Full size image

6 CONCLUSIONS

In this study, a stochastic fractional-order COVID-19 model was formulated. The existence and uniqueness of solutions was established, and two fractional operators (CF and ABC) were employed to examine the numerical dynamics of the COVID-19 disease in the light of the power-law and Mittag–Leffler function. A detailed numerical scheme for each operator in a stochastic standpoint was also presented. The probabilistic nature of the study presented the true picture of the COVID-19 dynamics in any affected community. The numerical schemes were used to simulate the theoretical results and the results indicate that the fractional-order derivative either helped increase or decrease the number of individuals in each compartment. In particular, we notice that the number of infectious individuals decrease with an increase in the fractional order, This suggests that a decrease in the fractional order can help curb the disease spread. The model was also fitted to data from the South Africa COVID-19 cases and the SARIMA technique for time series forecasting was used to predict the future behavior of COVID-19 with dead and infectious cases studied in South Africa. Using the stochastic approach, our results suggest the possibility of a continuous exponential growth of the pandemic and the spread of the fourth wave of the virus in South Africa.