Skip to main content
SpringerLink
Log in

Controlling of a mobile robot with a trailer and its nilpotent approximation

  • Nonlinear Dynamics & Mobile Robotics
  • Published:
Regular and Chaotic Dynamics Aims and scope Submit manuscript

Abstract

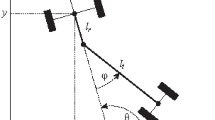
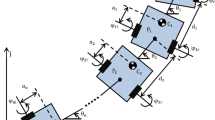
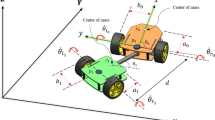
This work studies a number of approaches to solving the motion planning problem for a mobile robot with a trailer. Different control models of car-like robots are considered from the differential-geometric point of view. The same models can also be used for controlling a mobile robot with a trailer. However, in cases where the position of the trailer is of importance, i.e., when it is moving backward, a more complex approach should be applied. At the end of the article, such an approach, based on recent works in sub-Riemannian geometry, is described. It is applied to the problem of reparking a trailer and implemented in the algorithm for parking a mobile robot with a trailer.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Borisov, A. V., Kilin, A.A., and Mamaev, I. S., On the Hadamard–Hamel Problem and the Dynamics of Wheeled Vehicles, Regul. Chaotic Dyn., 2015, vol. 20, no. 6, pp. 752–766.

    Article  MathSciNet  MATH  Google Scholar 

  2. Markov, A.A., Some Examples of the Solution of a Special Kind of Problem on Greatest and Least Quantities, Soobshch. Kharkov. Mat. Obshch., Ser. 2, 1887, vol. 1, no. 5–6, pp. 250–276 (Russian).

    Google Scholar 

  3. Dubins, L.E., On Curves of Minimal Length with a Constraint on Average Curvature, and with Prescribed Initial and Terminal Positions and Tangents,Amer. J. Math., 1957, vol. 79, no. 3, pp. 497–516.

    MathSciNet  MATH  Google Scholar 

  4. Reeds, J.A. and Shepp, L.A., Optimal Paths for a Car That Goes Both Forwards and Backwards, Pacific J. Math., 1990, vol. 145, no. 2, pp. 367–393.

    Article  MathSciNet  Google Scholar 

  5. Sussmann, H. J. and Tang, G., Shortest Paths for the Reeds–Shepp Car: A Worked Out Example of the Use of Geometric Techniques in Nonlinear Optimal Control, Report SYCON-91-10, 1991.

    Google Scholar 

  6. Boissonnat, J.-D., Cérézo, A., and Leblond, J., Shortest Path of Bounded Curvature in the plane, Research Report, No. 1503, 1991.

    Google Scholar 

  7. Pontryagin, L. S., Boltyanskii, V.G., Gamkrelidze, R.V., and Mishchenko, E. F., The Mathematical Theory of Optimal Processes, L.W. Neustadt (Ed.), New York: Wiley, 1962.

  8. Laumond, J.-P., Feasible Trajectories for Mobile Robots with Kinematic and Environment Constraints, in Proc. on Intelligent Autonomous Systems, L.O. Hertzberger, F. C. A. Groen (Eds.), Amsterdam: North-Holland, 1987, pp. 346–354.

    Google Scholar 

  9. Euler, L., Methodus inveniendi lineas curvas maximi minimive proprietate gaudentes, sive solutio problematis isoperimitrici latissimo sensu accepti, Lausanne: Bousquet, 1744.

    MATH  Google Scholar 

  10. Saalschütz, L., Der belastete Stab unter Einwirkung einer seitlichen Kraft, Leipzig: Teubner, 1880.

  11. Born, M., Stabilität der elastischen Linie in Ebene und Raum: Unter verschiedenen Grenzbedingungen, Göttingen: Dieterich, 1906.

  12. Sachkov, Yu. L., Maxwell Strata in Euler’s Elastic Problem, J. Dyn. Control Syst., 2008, vol. 14, no. 2, pp. 169–234.

    Article  MathSciNet  MATH  Google Scholar 

  13. Agrachev, A.A. and Sachkov, Yu. L., Control Theory from the Geometric Viewpoint, Encyclopaedia Math. Sci., vol. 87, Berlin: Springer, 2004.

    Book  MATH  Google Scholar 

  14. Ardentov, A.A. and Sachkov, Yu. L., Extremal Trajectories in the Nilpotent Sub-Riemannian Problem on the Engel Group, Sb. Math., 2011, vol. 202, no. 11–12, pp. 1593–1615; see also: Mat. Sb., 2011, vol. 202, no. 11, pp. 31–54.

    Article  MathSciNet  MATH  Google Scholar 

  15. Brockett, R. W., and Dai, L., Non-Holonomic Kinematics and the Role of Elliptic Functions in Constructive Controllability, in Nonholonomic Motion Planning, Z. Li, J. F. Canny (Eds.), Boston: Kluwer, 1993, pp. 1–21.

    Chapter  Google Scholar 

  16. Jurdjevic, V., The Geometry of the Plate-Ball Problem, Arch. Rational Mech. Anal., 1993, vol. 124, no. 4, pp. 305–328.

    Article  MathSciNet  MATH  Google Scholar 

  17. Walsh, G. C., Montgomery, R., and Sastry, S. S., Optimal Path Planning on Matrix Lie Group, in Proc. of the 33rd IEEE Conf. on Decision and Control: Vol. 2, 1994, pp. 1258–1263.

    Google Scholar 

  18. Lawden, D. F., Elliptic Functions and Applications, Appl. Math. Sci., vol. 80, New York: Springer, 1989.

    Book  MATH  Google Scholar 

  19. Sachkov, Yu. L., Conjugate Points in Euler’s Elastic Problem, J. Dyn. Control Syst., 2008, vol. 14, no. 3, pp. 409–439.

  20. Sachkov, Yu. L. and Sachkova, E.L., Exponential Mapping in Euler’s Elastic Problem, J. Dyn. Control Syst., 2014, vol. 20, no. 4, pp. 443–464.

    Article  MathSciNet  MATH  Google Scholar 

  21. Ardentov, A.A. and Sachkov, Yu. L., Solution of Euler’s Elastic Problem, Autom. Remote Control, 2009, vol. 70, no. 4, pp. 633–643; see also: Avtomatika i Telemekhanika, 2009, no. 4, pp. 4–78.

    Article  MathSciNet  MATH  Google Scholar 

  22. Ardentov, A., Wolfram Demonstrations Project, http://demonstrationswolframcom/GenericEulersElastica/ (2012).

    Google Scholar 

  23. Montgomery, R., A Tour of Subriemannian Geometries, Their Geodesics and Applications, Math. Surveys Monogr., vol. 91, Providence,R.I.: AMS, 2002.

    MATH  Google Scholar 

  24. Moiseev, I. and Sachkov, Yu. L., Maxwell Strata in Sub-Riemannian Problem on the Group of Motions of a Plane, ESAIM Control Optim. Calc. Var., 2010, no. 16, pp. 16–380.

    Article  MathSciNet  MATH  Google Scholar 

  25. Sachkov, Yu. L., Conjugate and Cut Time in the Sub-Riemannian Problem on the Group of Motions of a Plane, ESAIM Control Optim. Calc. Var., 2010, no. 16, pp. 16–1018.

    Article  MathSciNet  Google Scholar 

  26. Sachkov, Yu. L., Cut Locus and Optimal Synthesis in the Sub-Riemannian Problem on the Group of Motions of a Plane, ESAIM Control Optim. Calc. Var., 2011, no. 17, pp. 17–293.

    Article  MathSciNet  MATH  Google Scholar 

  27. David, J. and Manivannan, P.V., Control of Truck-Trailer Mobile Robots: A Survey, Intel. Serv. Robot., 2014, vol. 7, no. 4, pp. 245–258.

    Article  Google Scholar 

  28. Lozano-Pérez, T., Spatial Planning: A Configuration Space Approach, IEEE Trans. Computers, 1983, vol.C-32, no. 2, pp. 108–120.

    Article  MathSciNet  MATH  Google Scholar 

  29. Barraquand, J. and Latombe, J.-C., On Non-Holonomic Mobile Robots and Optimal Maneuvering, in Proc. of IEEE Internat. Symp. on Intelligent Control (Albany,N.Y., 1989), pp. 340–347.

    Google Scholar 

  30. Laumond, J.-P., Jacobs, P., Taix, M., and Murray, R., A Motion Planner for Nonholonomic Mobile Robots, IEEE Trans. Robot. Autom., 1994, vol. 10, no. 5, pp. 577–593.

    Article  Google Scholar 

  31. Laumond, J.-P., Nonholonomic Motion Planning for Mobile Robots: Tutorial Notes, Toulouse: LAASCNRS, 1998.

    Book  Google Scholar 

  32. Chitsaz, H., On time-optimal trajectories for a car-like robot with one trailer, SIAM Conf. on Control and Its Applications (San Diego, Calif., 2013), pp. 114–120.

    Google Scholar 

  33. Agrachev, A.A. and Sarychev, A.V., Filtrations of a Lie Algebra of Vector Fields and the Nilpotent Approximation of Controllable Systems, Soviet Math. Dokl., 1988, vol. 36, no. 1, pp. 104–108; see also: Dokl. Akad. Nauk SSSR, 1987, vol. 295, no. 4, pp. 777–781.

    MathSciNet  MATH  Google Scholar 

  34. Hermes, H., Nilpotent and High-Order Approximations of Vector Field Systems, SIAM Rev., 1991, vol. 33, no. 2, pp. 238–264.

    Article  MathSciNet  MATH  Google Scholar 

  35. Laferriere, G. and Sussmann, H. J., A Differential Geometric Approach to Motion Planning, in Nonholonomic Motion Planning, Z. Li, J.F. Canny (Eds.), Boston: Kluwer, 1993, pp. 235–270.

    Chapter  Google Scholar 

  36. Agrachev, A. and Marigo, A., Nonholonomic Tangent Spaces: Intrinsic Construction and Rigid Dimensions, Electron. Res. Announc. Amer. Math. Soc., 2003, no. 9, pp. 9–111.

    Article  MathSciNet  MATH  Google Scholar 

  37. Mashtakov, A.P., Algorithms and Software Solving a Motion Planning Problem for Nonholonomic Fivedimensional Control Systems, Programmnye Sistemy: Teoriya i Prilozheniya, 2012, vol. 3, no. 1, pp. 3–29 (in Russian).

    Google Scholar 

  38. Bellaiche, A., The Tangent Space in Sub-Riemannian Geometry, in Sub-Riemannian Geometry, A. Bellaiche, J.-J. Risler (Eds.), Progr. Math., vol. 144, Basel: Birkhäuser, 1996, pp. 1–78.

    Chapter  Google Scholar 

  39. Ardentov, A.A. and Sachkov, Yu. L., Conjugate Points in Nilpotent Sub-Riemannian Problem on the Engel Group, J. Math. Sci., 2013, vol. 195, no. 3, pp. 369–390.

    Article  MathSciNet  MATH  Google Scholar 

  40. Ardentov, A.A. and Sachkov, Yu. L., Cut Time in Sub-Riemannian Problem on Engel Group, ESAIM Control Optim. Calc. Var., 2015, vol. 21, no. 4, pp. 958–988.

    Article  MathSciNet  MATH  Google Scholar 

  41. Wolfram, S., The Mathematica Book, 5th ed., Wolfram Media, 2003.

    MATH  Google Scholar 

  42. Bekkers, E. J., Duits, R., Mashtakov, A., and Sanguinetti, G.R., A PDE Approach to Data-Driven Sub-Riemannian Geodesics in SE(2), SIAM J. Imaging Sci., 2015, vol. 8, no. 4, pp. 2740–2770.

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Program Systems Institute of RAS, Pereslavl-Zalessky, Yaroslavl Region, 152020, Russia

    Andrey A. Ardentov

Authors
  1. Andrey A. Ardentov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Andrey A. Ardentov.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ardentov, A.A. Controlling of a mobile robot with a trailer and its nilpotent approximation. Regul. Chaot. Dyn. 21, 775–791 (2016). https://doi.org/10.1134/S1560354716070017

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1560354716070017

MSC2010 numbers

Keywords

Search

Navigation