Abstract
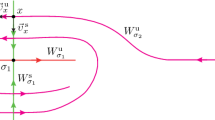
We consider regular Denjoy type homeomorphisms of the two-dimensional torus which are the most natural generalization of Denjoy homeomorphisms of the circle. In particular, they arise as Poincaré maps induced on global cross sections by leaves of one-dimensional orientable unstable foliations of some partially hyperbolic diffeomorphisms of closed three-dimensional manifolds. The nonwandering set of each regular Denjoy type homeomorphism is a Sierpiński set, and each such homeomorphism is, by definition, semiconjugate to the minimal translation on the two-dimensional torus. For regular Denjoy type homeomorphisms, we introduce a complete invariant of topological conjugacy characterized by the minimal translation, which is semiconjugate to the given regular Denjoy type homeomorphism, with a distinguished at most countable set of orbits.
Similar content being viewed by others
Notes
The rotation of the circle is defined as a map \(R(x) = x + \alpha \;({\text{mod}}\;1)\). A rotation R is minimal if and only if \(\alpha \in \mathbb{R}{{\backslash }}\mathbb{Q}\). The translation on the 2-torus is defined as a map \(g(x,y) = (x + \alpha ,y + \beta )\;({\text{mod}}\;1)\). A translation g is minimal if and only if the numbers α, β, and 1 are independent over the rational number field, i.e., if and only if \({{k}_{1}}\alpha + {{k}_{2}}\beta \) is not an integer for any pair of integers k1, k2, except for \({{k}_{1}} = {{k}_{2}} = 0.\)
By \({{p}^{{ - 1}}}(x)\) we mean the complete preimage of the point x.
By the closed embedded disk, we mean the image of the closed disk \(D = \{ ({{x}_{1}},{{x}_{2}}) \in {{\mathbb{R}}^{2}}\,{\text{|}}\,x_{1}^{2} + x_{2}^{2} \leqslant 1\} \) under the embedding \(\tau :D \to {{\mathbb{T}}^{2}}\).
In the one-dimensional case, according to [6], it is possible to construct a Denjoy homeomorphism of the circle with a characteristic set consisting of a countable number of orbits.
REFERENCES
D. Z. Arov, “Topological similitude of automorphisms and translations of compact commutative groups,” Usp. Mat. Nauk 18 (5), 133–138 (1963).
K. Kuratowski, Topology (Academic, New York, 1968), Vol. 2.
C. Bonatti and M. Viana, “SRB measures for partially hyperbolic systems whose central direction is mostly contracting,” Isr. J. Math. 115, 157–193 (2000).
K. Borsuk, “On embedding curves in surfaces,” Fundam. Math. 59, 73–89 (1966).
M. Carvalho, “Sinai–Ruelle–Bowen measures for N-dimensional derived from Anosov diffeomorphisms,” Ergodic Theory Dyn. Syst. 13 (1), 21–44 (1993).
A. Denjoy, “Sur les courbes définies par les équations différentielles à la surface du tore,” J. Math. Pures Appl. 11, 333–376 (1932).
V. Horita and M. Viana, “Hausdorff dimension for non-hyperbolic repellers II: DA diffeomorphisms,” Discrete Contin. Dyn. Syst. 13 (5), 1125–1152 (2005).
F. Kwakkel, “Minimal sets of non-resonant torus homeomorphisms,” Fundam. Math. 211 (1), 41–76 (2011).
N. G. Markley, “Homeomorphisms of the circle without periodic points,” Proc. London Math. Soc. 3 (20), 688–698 (1970).
P. D. McSwiggen, “Diffeomorphisms of the torus with wandering domains,” Proc. Am. Math. Soc. 117 (4), 1175–1186 (1993).
A. Norton and D. Sullivan, “Wandering domains and invariant conformal structures for mappings of the 2-torus,” Ann. Acad. Sci. Fenn. Math. 21 (1), 51–68 (1996).
A. Norton and J. A. Velling, “Conformal irregularity for Denjoy diffeomorphisms of the 2-torus,” Rocky Mountain J. Math. 24 (2), 655–671 (1994).
J. H. Poincaré, “Mémoire sur les courbes définies par les équations différentielles (III),” J. Math. Pures Appl. Ser. 4 1, 167–244 (1885).
G. T. Whyburn, “Topological characterization of the Sierpiński curve,” Fundam. Math. 45, 320–324 (1958).
Funding
The final version of the article was obtained with the financial support from the Russian Science Foundation grant (project no. 21-11-00010) with the use of materials obtained earlier with the financial support from the Russian Science Foundation grant (project no. 17-11-01041). Additionally, the proof of Theorem 2 was obtained with the financial support from the Laboratory of Dynamical Systems and Applications of the National Research University Higher School of Economics, grant of the Ministry of Science and Higher Education of the Russian Federation, agreement no. 075-15-2022-1101.
Author information
Authors and Affiliations
Corresponding authors
Ethics declarations
The authors declare that they have no conflicts of interest.
Additional information
Translated by I. Ruzanova
Rights and permissions
About this article
Cite this article
Grines, V.Z., Mints, D.I. On Topological Classification of Regular Denjoy Type Homeomorphisms. Dokl. Math. 106, 268–271 (2022). https://doi.org/10.1134/S106456242204010X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S106456242204010X