A Study of Nitric Oxide Generation in a Pulsed Periodic Diffuse Discharge in Air Flow

Abstract

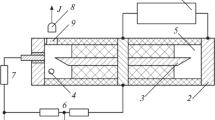
The results of experimental and computational studies of the pulsed periodic microsecond diffuse discharge excited in the air flow under atmospheric pressure in a sharply heterogeneous interval are described. It is shown that effective synthesis of nitric oxide is ensured in such a discharge. A model of the production of nitrogen oxides in the late stage of discharge has been developed, which takes into account the main plasmachemical reactions and gasdynamics. Simulation shows the combined effect of plasmachemical and gasdynamics processes on the spatiotemporal characteristics of the discharge, which determinethe generation of nitric oxide among others. The values of the main parameters of the discharge are determined, and satisfactory agreement between the calculated and experimental data is shown.

Appendices

APPENDIX 1

1.1 SPATIAL SAMPLING

Spatial discretization of equations (1) and (3) was performed by the Harten–Lax–van Leer contact (HLLC) finite volume method with a second order of accuracy [22]. Equations (1) and (3) can be written in general form with values of i and i + 1 at the boundary of the calculation cell between nodes, in which the desired values in time step m are defined as follows:

$$\begin{gathered} \frac{{\partial Q}}{{\partial t}} + \frac{{\partial F(Q)}}{{\partial r}} = {{S}_{Q}}, \\ Q(r,0) = \left\{ \begin{gathered} {{Q}_{L}} \equiv Q_{i}^{m}\quad \,{\text{if}}\quad r < 0, \hfill \\ {{Q}_{R}} \equiv Q_{{i + 1}}^{m}\quad {\text{if}}\quad r > 0. \hfill \\ \end{gathered} \right. \\ \end{gathered} $$

(5)

The flux values at the boundary of the calculation cell are defined in the following fashion:

$$F_{{i + \frac{1}{2}}}^{{{\text{HLLC}}}} = \left\{ \begin{gathered} {{F}_{L}}\quad \;{\text{if}}\quad 0 \leqslant {{S}_{L}}, \hfill \\ {{F}_{{*L}}}\quad {\text{if}}\quad {{S}_{L}} \leqslant 0 \leqslant {{S}_{*}}, \hfill \\ {{F}_{{*R}}}\quad {\text{if}}\quad {{S}_{*}} \leqslant 0 \leqslant {{S}_{R}}, \hfill \\ {{F}_{R}}\quad \;{\text{if}}\quad 0 \geqslant {{S}_{R}}, \hfill \\ \end{gathered} \right.$$

(6)

where

$$\begin{gathered} {{F}_{{*L}}} = {{F}_{L}} + {{S}_{L}}({{Q}_{{*L}}} - {{Q}_{L}}), \\ {{F}_{{*R}}} = {{F}_{R}} + {{S}_{R}}({{Q}_{{*R}}} - {{Q}_{R}}), \\ \end{gathered} $$

(7)

and ${{F}_{L}}$ and ${{F}_{R}}$ are the fluxes at nodes i and i + 1, respectively. The ${{Q}_{{*K}}}$ values, where $K = L,R$, for the gasdynamics system of equations (1) are determined as follows:

$$\begin{gathered} {{Q}_{{*K}}} = {{\rho }_{K}}\left( {\frac{{{{S}_{K}} - {{u}_{K}}}}{{{{S}_{K}} - {{S}_{*}}}}} \right) \\ \, \times \left[ \begin{gathered} {\text{ }}1 \hfill \\ {\text{ }}{{S}_{*}} \hfill \\ \frac{{{{E}_{K}}}}{{{{\rho }_{K}}}} + \left( {{{S}_{*}} - {{u}_{K}}} \right)\left[ {{{S}_{*}} + \frac{{{{p}_{K}}}}{{{{\rho }_{K}}\left( {{{S}_{K}} - {{u}_{K}}} \right)}}} \right] \hfill \\ \end{gathered} \right], \\ \end{gathered} $$

(8)

where ${{p}_{K}}$, ${{\rho }_{K}},$ ${{u}_{K}}$, and ${{E}_{K}}$ are the pressure, density, velocity, and total energy at the corresponding boundary of the computational cell, respectively.

For equations of type (3), ${{Q}_{{*K}}}$ has the following form:

$${{Q}_{{*K}}} = {{n}_{K}}\left( {\frac{{{{S}_{K}} - {{u}_{K}}}}{{{{S}_{K}} - {{S}_{*}}}}} \right),$$

(9)

where ${{n}_{K}}$ is the concentration of the plasma component at the corresponding cell boundary.

In accordance with [22], the expressions for ${{S}_{K}}$ and ${{S}_{*}}$ are defined as follows:

$${{S}_{L}} = {{u}_{L}} - {{a}_{L}}{{q}_{L}},\quad {{S}_{L}} = {{u}_{L}} - {{a}_{L}}{{q}_{L}},$$

$$\begin{gathered} {{q}_{K}} = \left\{ \begin{gathered} 1\quad {\text{if}}\quad {{{\bar {p}}}_{*}} \leqslant {{p}_{K}}, \hfill \\ {{\left[ {1 + \frac{{{{\gamma }_{K}} + 1}}{{2{{\gamma }_{K}}}}\left( {\frac{{{{{\bar {p}}}_{*}}}}{{{{p}_{K}}}} - 1} \right)} \right]}^{{1/2}}}\quad {\text{if}}\quad {{{\bar {p}}}_{*}} > {{p}_{K}}, \hfill \\ \end{gathered} \right. \\ {{a}_{K}} = {{\left( {\frac{{{{\gamma }_{K}}{{p}_{K}}}}{{{{\rho }_{K}}}}} \right)}^{{1/2}}}, \\ \end{gathered} $$

(10)

$${{S}_{*}} = \frac{{{{p}_{R}} - {{p}_{L}} + {{\rho }_{L}}{{u}_{L}}({{S}_{L}} - {{u}_{L}}) - {{\rho }_{R}}{{u}_{R}}({{S}_{R}} - {{u}_{R}})}}{{{{\rho }_{L}}({{S}_{L}} - {{u}_{L}}) - {{\rho }_{R}}({{S}_{R}} - {{u}_{R}})}}.$$

Pressure ${{\bar {p}}_{*}}$ is approximated as in [23]:

$$\begin{gathered} {{p}_{s}} = \frac{1}{2}({{p}_{L}} + {{p}_{R}}) - \frac{1}{8}({{u}_{R}} - {{u}_{L}})({{a}_{R}} + {{a}_{L}})({{\rho }_{R}} + {{\rho }_{L}}), \\ {{{\bar {p}}}_{*}} = \max (0,{{p}_{s}}). \\ \end{gathered} $$

(11)

APPENDIX 2

1.1 TIME INTEGRATION

Time integration was performed the basis of an explicit predictor–corrector scheme (trapezoid rule) with the second order of accuracy. If the differential equation for particles from system (1) is expressed as $y{\kern 1pt} '(t) = f(t,y)$, then its solution is found as follows:

$$\begin{gathered} \tilde {y} = {{y}_{n}} + \tau f({{t}_{n}},{{y}_{n}}), \\ {{y}_{{n + 1}}} = {{y}_{n}} + \frac{\tau }{2}\left[ {f({{t}_{n}},{{y}_{n}}) + f({{t}_{{n + 1}}},\tilde {y})} \right]. \\ \end{gathered} $$

(12)

To determine time step $\tau$, a combination of characteristic times was used, in a way as it was done in [22, 24]:

$$\begin{gathered} \tau = 0.9{{\tau }_{{CD}}}, \\ {{\tau }_{{CD}}} = \min \left[ {\frac{1}{{\frac{1}{{{{\tau }_{C}}}} + \frac{1}{{{{\tau }_{D}}}}}},0.5{{\tau }_{C}},0.4{{\tau }_{S}}} \right], \\ \end{gathered} $$

$${{\tau }_{S}} = \frac{1}{{\left| {\min \left[ {\delta ,\frac{{{{S}_{n}}}}{n}} \right]} \right|}},\quad \delta = {\text{1}}{{{\text{0}}}^{{ - 100}}},$$

(13)

$$\begin{gathered} \tau _{D}^{{}} = \frac{{{{h}^{2}}}}{{2(a + \delta )}},\quad \tau _{C}^{{}} = \frac{h}{{\max (\left| {u - c} \right|,\left| u \right|,\left| {u + c} \right|)}}, \\ a = \max \left( {\frac{{\lambda (\gamma - 1)T}}{p},D} \right),\quad c = {{\left( {\frac{{\gamma p}}{\rho }} \right)}^{{1/2}}}, \\ \end{gathered} $$

where ${{\tau }_{S}}$ is the time determined for each type of particles as the ratio of concentration n to source ${{S}_{n}}$ of birth and death of these particles in accordance with Eq. (3). If $S \geqslant 0$, then ${{\tau }_{S}} \to \infty$, and the expression for ${{\tau }_{{CD}}}$ is exactly the same as that given in [25]. The use of small value δ makes it possible to exclude division by zero. The introduction of ${{\tau }_{S}}$ is justified by that there should be no negative values for the concentration of particles as a result of plasmachemical reactions; ${{\tau }_{C}}$ and ${{\tau }_{D}}$ are the maximum possible times for convection and diffusion in accordance with the Courant criterion. It should be noted that ${{\tau }_{C}}$ is determined only by gasdynamics with accounting for the compressibility of the medium (c is the speed of sound), since there is no drift of charged particles, while ${{\tau }_{D}}$ is determined not only by the diffusion of all components, but also by thermal diffusivity $\lambda (\gamma - 1)T{\text{/}}p$ on the basis of equation (1) for the energy.