Abstract
We propose a new method for solving an important problem of astronomy that arises in observations with ultrahigh-angular-resolution interferometers. This method is based on the application of the theory of artificial neural networks. We propose and compute a multiparameter model for a celestial object like Sgr A*. For this model we have numerically constructed a number of probable images for neural network training. After neural network training on these images, the quality of its operation has been tested on another series of images from the same model. We have proven that a neural network can recognize and classify celestial objects (also obtained from interferometers) virtually no worse than can be done by a human.






Similar content being viewed by others
Notes
1 μas ≈ 4.8 × 10–12 rad.
In the model itself we add not bright points, but bright circles whose radius is proportional to the star’s model brightness to the pictures, because the numerical simulations of point objects yield inadequate results compared to the simulations of extended objects. Furthermore, in real telescopes stars give images precisely in the form of circles (rather than points); the brighter the star, the bigger the circle. In the subsequent Fourier transforms we simulate the same stars precisely as points (delta functions).
REFERENCES
A. R. Thompson, J. M. Moran, and G. W. Swenson, Jr., Interferometry and Synthesis in Radio Astronomy (Wiley, New York, 2001).
K. I. Kellermann and J. M. Moran, Ann. Rev. Astron. Astrophys. 39, 457 (2001).
A. Quirrenbach, Ann. Rev. Astron. Astrophys. 39, 353 (2001).
A. Quirrenbach, ISSI Sci. Rep. Ser. 9, 293 (2010).
R.-S. Lu, A. E. Broderick, F. Baron, J. D. Monnier, V. L. Fish, S. S. Doeleman, and V. Pankratius, Astrophys. J. 788, 120 (2014).
N. S. Kardashev, V. V. Khartov, V. V. Abramov, et al., Astron. Rep. 57, 154 (2013).
P. Coles and L.-Y. Chiang, Nature (London, U.K.) 406, 376 (2000).
L.-Y. Chiang et al., Astrophys. J. 590, L65 (2003).
A. B. Kamruddin and J. Dexter, Mon. Not. R. Astron. Soc. 434, 765 (2013).
A. A. Shatskii, Yu. Yu. Kovalev, and I. D. Novikov, J. Exp. Theor. Phys. 120, 798 (2015).
V. V. Kruglov and V. V. Borisov, Artificial Neural Networks. Theory and Practice (Goryachaya Liniya, Telekom, Moscow, 2002) [in Russian].
R. Hadsell, S. Chopra, and Y. LeCun, Dimensionality Reduction by Learning an Invariant Mapping. http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf. Accessed 2006
K. V. Vorontsov, Neural Networks, Video Course. https://www.youtube.com/watch?v=WjwA5DqxL-c. Accessed 2016
F.-F. Li, J. Johnson, and S. Yeung, Convolutional Neural Networks. http://cs231n.stanford.edu/syllabus.html. Accessed 2018
K. Ehsani, H. Bagherinezhad, J. Redmon, R. Mottaghi, and A. Farhadi, arXiv:1803.10827.
J. Redmon and A. Farhadi, arXiv:1804.02767.
D. Gordon, A. Kembhavi, M. Rastegari, J. Redmon, D. Fox, and A. Farhadi, arXiv:1712.03316.
J. Redmon and A. Farhadi, arXiv:1612.08242.
M. Rastegari, V. Ordonez, J. Redmon, and A. Farhadi, arXiv:1603.05279.
J. Redmon, S. Divvala, R. Girshick, and A. Farhadi, arXiv:1506.02640.
J. Redmon and A. Angelova, arXiv:1412.3128.
A. Bochkovskiy, https://github.com/AlexeyAB/darknet.
Author information
Authors and Affiliations
Corresponding author
Additional information
Translated by V. Astakhov
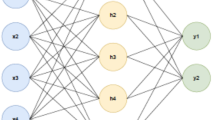
Architecture of the YOLOv3 Neural Net
Architecture of the YOLOv3 Neural Net
The architecture of the YOLOv3 neural net is based on Darknet-53 (the number in the name means the number of convolutional layers in the architecture). The architecture uses residual blocks and unsampling and, basically, makes detection in three scales by dividing the image into 13 × 13, 26 × 26, and 52 × 52 cells. At the output we obtain three tensors 13 × 13 × (B × (5 + C)), 26 × 26 × (B × (5 + C)), and 52 × 52 × (B × (5 + C)), where B is the number of frames whose center is in the cell, the frame sizes can be outside the cell, C are the probabilities of classes from the data set (their sum is equal to unity), number 5 denotes five parameters: the probability P that an object was detected in a given cell, the coordinates of the frame are x and y, its height and width are h and w. The number of frames B greater than one is also needed for such situations where the centers of two objects are located in one cell (for example, a pedestrian against the background of a car). For example, for B = 2 and C = 3 for each cell in three scales we will obtain 3549 (13 ⋅ 13 + 26 ⋅ 26 + 52 ⋅ 52) vectors P1, x1, y1, w1, h1, C1_1, C1_2, C1_3, P2, x2, y2, w2, h2, C2_1, C2_2, and C2_3, out of which we will filter out only those we need. In the YOLOv3 architecture B = 3. Returning to the question about the probability (prob) that the code gives for each object found by it, this is the probability P multiplied by C of the class whose score probability (C1_1, C1_2, C1_3) is maximal for a given frame.
Rights and permissions
About this article
Cite this article
Shatskiy, A.A., Evgeniev, I.Y. Neural Network Astronomy as a New Tool for Observing Bright and Compact Objects. J. Exp. Theor. Phys. 128, 592–598 (2019). https://doi.org/10.1134/S106377611903021X
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S106377611903021X