The Sound Field in a Marine Waveguide with a Cylindrical Inhomogeneity

Abstract

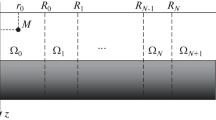
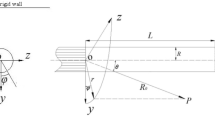
A three-dimensional analytical solution is constructed for the model of an inhomogeneous hydroacoustic waveguide with a cylindrical inhomogeneity within the sedimentary layer. A numerical-analytical method for finding the velocity potential is proposed, for which undefined coefficients for normal modes are determined from the corresponding infinite system of linear algebraic equations. The asymptotic behavior of the amplitude coefficients in the system is investigated. Sound fields with variation of the parameters of the problem are numerically studied.

ANALYSIS OF THE DISPERSION EQUATION FOR A TWO-LAYER WAVEGUIDE

Let us consider the behavior of the roots of dispersion equations (18)–(21) with $n \to \infty .$ Taking into account the fact that with increasing ordinal number n, if there is no attenuation in the sedimentary layer, the eigenvalues become purely imaginary ξ_{j, n} = iw (j = 0, 2); both these equations can be written in the form

$${\text{tg}}\sqrt {k_{{\text{0}}}^{2} + {{w}^{2}}} {{h}_{{\text{0}}}}\,{\text{tg}}\sqrt {k_{{\text{1}}}^{2} + {{w}^{2}}} H = \frac{{{{{\rho }}_{1}}}}{{{{{\rho }}_{0}}}}\sqrt {\frac{{k_{{\text{0}}}^{2} + {{w}^{2}}}}{{k_{{\text{1}}}^{2} + {{w}^{2}}}}} ,$$

((A1))

where ${{h}_{{\text{0}}}}$ the thickness of the water layer and H is the thickness of the bottom layer.

Since the eigenvalues increase with increasing ordinal number, i.e., ${{w}^{2}} \to + \infty ,$ we obtain the asymptotic approximation for Eq. (A1):

$${\text{tan}}\,{{w}_{n}}{{h}_{{\text{0}}}}\,{\text{tan}}\,{{w}_{n}}H = \frac{{{{{\rho }}_{1}}}}{{{{{\rho }}_{0}}}}.$$

((A2))

Further, let us suppose that the depths of the water and bottom layers can be represented through some characteristic size a as follows:

$${{h}_{0}} = Ma,\,\,\,\,H = La,\,\,\,\,M,L \in {\mathbf{N}},$$

then, Eq. (A2) can be solved exactly. Indeed, in this case, Eq. (A2) can be written as

$${\text{tan}}\,Mt\,{\text{tan}}\,Lt = \frac{{{{{\rho }}_{1}}}}{{{{{\rho }}_{0}}}},$$

((A3))

where $t = aw.$ However, by virtue of the trigonometric formulas

$${\text{tan}}\,Mt = \frac{{\sum\limits_{k = 0}^{\left[ {\frac{{M - 1}}{2}} \right]} {{{{( - 1)}}^{k}}C_{M}^{{2k + 1}}{\text{ta}}{{{\text{n}}}^{{{\text{2}}k + {\text{1}}}}}t} }}{{\sum\limits_{k = 0}^{\left[ {\frac{M}{2}} \right]} {{{{( - 1)}}^{k}}C_{M}^{{2k}}{\text{t}}{{{\text{g}}}^{{{\text{2}}k}}}t} }},$$

((A4))

([x] means the whole part of the real x axis), Eq. (A3) is brought by substitution of ${\text{tan}}\,t = Z$ to a rational equation of the form

$$\begin{gathered} {{\rho }_{0}}\sum\limits_{k = 0}^{\left[ {\frac{{M - 1}}{2}} \right]} {{{{( - 1)}}^{k}}C_{M}^{{2k + 1}}{{Z}^{{2k + 1}}}} \sum\limits_{k = 0}^{\left[ {\frac{{L - 1}}{2}} \right]} {{{{( - 1)}}^{k}}C_{L}^{{2k + 1}}{{Z}^{{2k + 1}}}} \\ = {{\rho }_{1}}\sum\limits_{k = 0}^{\left[ {\frac{M}{2}} \right]} {{{{( - 1)}}^{k}}C_{M}^{{2k}}{{Z}^{{2k}}}} \sum\limits_{k = 0}^{\left[ {\frac{L}{2}} \right]} {{{{( - 1)}}^{k}}C_{L}^{{2k}}{{Z}^{{2k}}}} . \\ \end{gathered} $$

((A5))

Equation (A5) is an algebraic equation of order (M + L) if the parity of numbers M and L coincide, otherwise, it is of order (M + L – 1). We denote the order of this equation as p. As is known, this equation cannot have more than p real roots; then, if {Z_l} (l = 1, 2, …, q; q ≤ p) real roots of (A5), we have the following set of roots (A2):

$${{w}_{{l,n}}} = \frac{1}{a}{\text{arctan }}{{Z}_{l}} + \frac{{{\pi }n}}{a}$$

or considering that $a = \frac{M}{{{{h}_{0}}}} = \frac{L}{H},$ we obtain the asymptotics for the eigenvalues

$${{\xi }_{{j,n}}} = \frac{{i{\pi }M}}{{{{h}_{{\text{0}}}}q}}n + O(1),\,\,\,\,n \to \infty .$$

((A6))