Skip to main content
SpringerLink
Log in

On Integral Equations of Cracks of a New Type

  • Published:
Vestnik St. Petersburg University, Mathematics Aims and scope Submit manuscript

Abstract

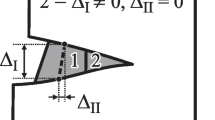
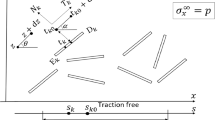
For the first time, the paper develops a method for the modeling of cracks of a new type that allows their description in environments of complex rheologies. It is based on a new universal modeling method previously published by us and used in boundary-value problems for systems of partial differential equations. The advantage of the method is the possibility of avoiding the need to solve complex boundary-value problems for systems of partial differential equations by replacing them with separate differential equations, among which the Helmholtz equations are the simplest. Namely, with the help of combinations of solutions to boundary-value problems for this equation, it is possible to describe the behavior of complex solutions of multicomponent boundary-value problems. In this paper, for the first time, the method is applied to a mixed boundary-value problem for cracks of a new type. Cracks of a new type, complementing Griffiths cracks, were discovered during the study of fractures of lithospheric plates that converge at the ends when meeting along the Conrad discontinuity. In the course of the study, Kirchhoff plates were adopted as models of lithospheric plates. The method developed in the published article is aimed at the possibility of describing models of approaching objects similar to lithospheric plates in the form of deformable plates of more complex rheologies. In particular, it can be a thermoelectroelastic plate or other rheology. In the process of solving the problems using Kirchhoff models for lithospheric plates, there is the problem of calculating some functionals that needed to be determined. This method demonstrates an approach that eliminates this drawback. The derivation of integral equations of cracks of a new type, the method of their solution, and the approach to application in more complex rheologies are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. A. A. Griffith, “The phenomena of rupture and flow in solids,” Trans. R. Soc. A 221, 163–198 (1921). https://doi.org/10.1098/rsta.1921.0006

    Article  MATH  Google Scholar 

  2. C. Sator and W. Becker, “Closed-form solutions for stress singularities at plane bi- and trimaterial functions,” Arch. Appl. Mech. 82, 643–658 (2012). https://doi.org/10.1007/s00419-011-0580-6

    Article  MATH  Google Scholar 

  3. G. Irwin, “Fracture dynamics,” in Fracturing of Metals (American Society for Metals, Cleveland, Oh., 1948), pp. 147–166.

  4. J. B. Leblond and J. Frelat, “Crack kinking from an interface crack with initial contact between the crack lips,” Eur. J. Mech. - A/Solids 20, 937–951 (2001). https://doi.org/10.1016/S0997-7538(01)01173-1

    Article  MATH  Google Scholar 

  5. V. V. Loboda and A. E. Sheveleva, “Determing prefracture zones at a crack tip between two elastic orthotropic bodies,” Int. Appl. Mech. 39, 566–572 (2003). https://doi.org/10.1023/A:1025139625891

    Article  MATH  Google Scholar 

  6. J. F. Loeber and G. C. Sih, “Transmission of anti-plane shear waves past an interface crack in dissimilar media,” Eng. Fract. Mech. 5, 699–725 (1973). https://doi.org/10.1016/0013-7944(73)90048-9

    Article  Google Scholar 

  7. O. V. Menshykov, M. V. Menshykova, and I. A. Guz, “3-D elastodynamic contact problem for an interface crack under harmonic loading,” Eng. Fract. Mech. 80, 52–59 (2012). https://doi.org/10.1016/j.engfracmech.2010.12.010

    Article  Google Scholar 

  8. O. V. Menshykov, M. V. Menshykova, I. A. Guz, and V. Mikucka, “2-D and 3-D contact problems for interface cracks under harmonic loading,” in Integral Methods in Science and Engineering, Ed. by C. Constanda and P. Harris (Birkhäuser, Boston, 2011), pp. 241–252. https://doi.org/10.1007/978-0-8176-8238-5_23

    Book  MATH  Google Scholar 

  9. O. V. Menshykov, M. V. Menshykov, and I. A. Guz, “Linear interface crack under plane shear wave,” CMES— Comput. Model. Eng. Sci. 48, 107–120 (2009). https://doi.org/10.3970/cmes.2009.048.107

    Article  MathSciNet  MATH  Google Scholar 

  10. O. V. Menshykov, M. V. Menshykova, and I. A. Guz, “Modelling crack closure for an interface crack under harmonic loading,” Int. J. Fract. 165, 127–134 (2010). https://doi.org/10.1007/s10704-010-9492-7

    Article  MATH  Google Scholar 

  11. O. V. Menshykov, M. V. Menshykova, and I. A. Guz, “An iterative BEM for the dynamic analysis of interface crack contact problems,” Eng. Anal. Boundary Elem. 35, 735–749 (2011). https://doi.org/10.1016/j.enganabound.2010.12.005

    Article  MathSciNet  MATH  Google Scholar 

  12. V. V. Mikhas’kiv and I. O. Butrak, “Stress concentration around a spheroidal crack caused by a harmonic wave incident at an arbitrary angle,” Int. Appl. Mech. 42, 61–66 (2006). https://doi.org/10.1007/s10778-006-0059-2

    Article  Google Scholar 

  13. J. R. Rice, “Elastic fracture mechanics concepts for interfacial cracks,” J. Appl. Mech. 55, 98–103 (1988). https://doi.org/10.1115/1.3173668

    Article  Google Scholar 

  14. Ch. Zhang and D. Gross, On Wave Propagation in Elastic Solids with Cracks (Computational Mechanics, South-Hampton, U.K., 1998).

    MATH  Google Scholar 

  15. N. F. Morozov, Mathematical Problems in the Theory of Cracks (Nauka, Moscow, 1984) [in Russian].

    Google Scholar 

  16. G. P. Cherepanov, Brittle Fracture Mechanics (Nauka, Moscow, 1974) [in Russian].

    Google Scholar 

  17. M. S. Kirugulige and H. V. Tippur, “Mixed-mode dynamic crack growth in functionally graded glass-filled epoxy,” Exp. Mech. 46, 269–281 (2006). https://doi.org/10.1007/s11340-006-5863-4

    Article  Google Scholar 

  18. Y. Huang and H. Gao, “Intersonic crack propagation — Part II: Suddenly stopping crack,” J. Appl. Mech. 69, 76–80 (2002). https://doi.org/10.1115/1.1410936

    Article  MATH  Google Scholar 

  19. Y. A. Antipov and A. V. Smirnov, “Subsonic propagation of a crack parallel to the boundary of a half-plane,” Math. Mech. Solids 18, 153–167 (2013). https://doi.org/10.1177/1081286512462182

    Article  MathSciNet  MATH  Google Scholar 

  20. G. B. Sinclair, “Stress singularities in classical elasticity — I: Removal, interpretation, and analysis,” Appl. Mech. Rev. 57, 251–298 (2004). https://doi.org/10.1115/1.1762503

    Article  Google Scholar 

  21. G. B. Sinclair, “Stress singularities in classical elasticity — II: Asymptotic identification,” Appl. Mech. Rev. 57, 385–439 (2004). https://doi.org/10.1115/1.1767846

    Article  Google Scholar 

  22. V. A. Babeshko, O. V. Evdokimova, and O. M. Babeshko, “On the possibility of predicting some types of earthquake by a mechanical approach,” Acta Mech. 229, 2163–2175 (2018). https://doi.org/10.1007/s00707-017-2092-0

    Article  MathSciNet  MATH  Google Scholar 

  23. V. A. Babeshko, O. V. Evdokimova, and O. M. Babeshko, “On a mechanical approach to the prediction of earthquakes during horizontal motion of lithospheric plates,” Acta Mech. 229, 4727–4739 (2018). https://doi.org/10.1007/s00707-018-2255-7

    Article  MathSciNet  MATH  Google Scholar 

  24. V. A. Babeshko, O. M. Babeshko, and O. V. Evdokimova, “A new type of cracks adding to Griffith−Irwin cracks,” Dokl. Phys. 64, 102–105 (2019). https://doi.org/10.1134/S1028335819030042

    Article  Google Scholar 

  25. V. A. Babeshko, O. V. Evdokimova, and O. M. Babeshko, “Influence of the spatial model of lithospheric plates on an initial earthquake,” Dokl. Phys. 63, 203–207 (2018). https://doi.org/10.1134/S102833581805004X

    Article  MATH  Google Scholar 

  26. V. A. Babeshko, O. V. Evdokimova, and O. M. Babeshko, “Fractal properties of block elements and a new universal modeling method,” Dokl. Akad. Nauk, Fiz., Tekh. Nauki 499, 30–35 (2021). https://doi.org/10.31857/S2686740021040039

    Article  Google Scholar 

  27. V. A. Babeshko, O. V. Evdokimova, and O. M. Babeshko, “Stages of transformation of block elements,” Dokl. Phys. 61, 227–231 (2016). https://doi.org/10.1134/S1028335816050049

    Article  Google Scholar 

  28. I. I. Vorovich and V. A. Babeshko, Dynamic Mixed Problems of Elasticity Theory for Non-Classical Domains (Nauka, Moscow, 1979) [in Russian].

    MATH  Google Scholar 

  29. B. Noble, Methods Based on the Wiener–Hopf Technique for the Solution of Partial Differential Equations (Pergamon, New York, 1958; Insotrannaya Literatura, Moscow, 1962).

Download references

Funding

Some parts of the work were completed as part of implementation of the state assignment of the Russian Ministry of Education and Science for 2022 (project no. FZEN-2020-0020), were supported by the Southern Scientific Center of the Russian Academy of Sciences (project no. 00-20-13, state registration number 122020100341-0) and by the Russian Foundation for Basic Research (project nos. 19-41-230003, 19-41-230004, and 19-48-230014).

Author information

Authors and Affiliations

  1. Southern Scientific Center, Russian Academy of Sciences, 344006, Rostov-on-Don, Russia

    V. A. Babeshko & O. V. Evdokimova

  2. Kuban State University, 350040, Krasnodar, Russia

    V. A. Babeshko & O. M. Babeshko

Authors
  1. V. A. Babeshko
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. V. Evdokimova
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. O. M. Babeshko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to V. A. Babeshko, O. V. Evdokimova or O. M. Babeshko.

Ethics declarations

The authors declare that they have no conflicts of interest.

Additional information

Translated by E. Oborin

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Babeshko, V.A., Evdokimova, O.V. & Babeshko, O.M. On Integral Equations of Cracks of a New Type. Vestnik St.Petersb. Univ.Math. 55, 267–274 (2022). https://doi.org/10.1134/S1063454122030049

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1063454122030049

Keywords:

Search

Navigation