What Comes First: The Egg or the Mathematics? Review Article

Abstract

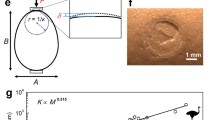
When we wish to describe our Universe, our planet Earth, natural environment, and our surroundings, artists often use imagery, whereas scientists attempt to use mathematical formulae. It begs the fundamental question: was the nature and the universe preceded by a clear mathematical design, or did the mathematic description appear subsequently? In this review, we addressed a biological issue of shapes in nature and, specifically, egg shapes in birds, including poultry, as one of most exciting avian adaptations. In order to compute the shape and volume of eggs as a marker of fitness, discover subtle nuances of the evolution of nest parasitism as in cuckoos, detect double-yolk eggs in poultry, develop methods for hatchability improvement and in ovo sex identification, and other things, an exact description of egg shape is urgently needed. We overviewed here the recent mathematical development of a universal egg shape equation called the Narushin–Romanov–Griffin (NRG) model. Following the Latin term “ab ovo” meaning “from the beginning, the origin, the egg,” the NRG model successfully tried to combine two concepts, biological object and mathematical geometry, and enabled to fulfil the formidable task of describing, mathematically, any bird’s egg. Eventually, a series of mathematical formulae was developed that could define bird eggs of any shape present in nature including spherical, elliptical, ovoid and pear-shaped ones.