Measuring the Acoustic Characteristics of Compact Concrete Building Structures Using the Impact Echo Method

Abstract

The impact-echo method, which is a method of free vibrations, is used for testing building structures made of concrete that have the measured thickness $H$ at least six times smaller than the other dimensions and is not used to test compact products in which the thickness $H$ is comparable to the other dimensions. The problem with testing compact objects is that it is impossible to unambiguously determine the required resonant frequency ${{f}_{0}}\sim {\text{1/}}H$ determined by the product thickness $H$ on the spectrum of the compact product against the background of closely spaced numerous resonances determined by other test object dimensions. Another reason is that due to a strong influence of the geometric dispersion of the sound speed in compact products, it is necessary to calculate a correction factor $\beta$ for each new compact test object. The article proposes a solution to the problem of testing compact concrete building structures using a multiplicative impact echo method that allows one to determine the desired resonant frequency, as well as using various versions of the correlation impact echo method that allow one to measure the speed of sound in compact products for the subsequent determination of concrete strength both in the process of cement solidification and during the operation of building structures in order to predict the trouble-free service life of buildings and structures.

INTRODUCTION

One of the main problems of testing concrete building structures (BSs) testing is BS thickness gauging, as well as the measurement of the propagation velocity of acoustic vibrations in concrete; this is used to judge the concrete strength. However, the anomalously high attenuation of ultrasound in concrete does not allow one to test a BS with a thickness of more than 1.5 m using ultrasonic (US) nondestructive testing methods [1]. Therefore, to test the plane-parallel BSs with a thickness of 1.5 m or more, one uses acoustic methods based on analyzing eigenfrequencies—the resonance method (a forced vibration method) or the impact-echo method (a free vibration method). In both cases, resonant vibrations are established in the concrete product, the frequency of the vibrations is determined by the product thickness, ${{f}_{0}}~\sim {\text{1/}}H$. Due to the fact that the resonance frequency is low when testing products with a large thickness, the attenuation of the acoustic signal will be small. For this reason, by using eigenfrequency methods, it is possible to control BSs with a thickness reaching several meters.

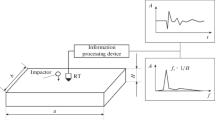
At present, the impact-echo method [2–5] is the method most widely used for testing concrete BSs, where a special device (impactor) is used to produce a mechanical impact on the test object surface short in duration but sufficient in strength. This impact initiates free acoustic damped vibrations in the test object (TO) that are detected by a receiving transducer (RT) located at a short distance from the impactor. The received acoustic signal is transduced into an electrical signal in the RT and then digitized and fed to the processing device, at the output of which it is presented in the time and frequency domains. The TO parameters are determined by the amplitude-frequency characteristic (AFC) where the pronounced maximum is observed at the resonant frequency ${{f}_{0}}$. In turn, the product thickness $H\sim {\text{1/}}{{f}_{0}}$ is estimated based on the maximum.

As is well known, resonance methods provide high measurement accuracy, and if the attenuation is small, then the relative frequency measurement error does not exceed 0.5% [1]. However, when using the impact echo method, an additional error occurs causing the acoustic wave velocity in real concrete BSs of the “slab” type to be approximately 96% of the longitudinal wave velocity ${{C}_{P}}$, that is, the real sound velocity in the slab is ${{C}_{{PP}}} = 0.96{{C}_{P}}$ [6]. This error is related to the geometric dispersion of the speed of sound [7]. To eliminate this error, the empirical coefficient $\beta = 0.96$ was introduced in the TO of the “slab” type [6, 7]. That is why, when testing plates by the impact echo method, it is necessary to use the velocity value ${{C}_{{PP}}}$ that, in case of a plate, is determined by a Lamb wave [6],

$${{C}_{{PP}}} = 2{{f}_{0}}H = \beta {{C}_{P}},$$

(1)

where ${{f}_{0}}$ is the maximum amplitude frequency in the spectrum, $H$ is the test product thickness, $\beta$ is a coefficient correcting the influence of the geometric dispersion of the speed of sound, and ${{C}_{P}}$ is the propagation velocity of longitudinal acoustic vibrations in concrete calculated for an infinite half-space.

In turn, as is well known, the velocity of the longitudinal sound wave ${{C}_{P}}$ in products with unlimited dimensions, such as an infinite half-space, depends only on the properties of the material [1],

$${{C}_{P}} = \sqrt {\frac{{E(1 - \nu )}}{{\rho (1 + \nu )(1 - 2\nu )}}} ,$$

(2)

where $E$ is Young’s modulus, $\nu$ is Poisson’s ratio, and $\rho$ is the density.

However, the correction factor $\beta = 0.96$ is considered to be known and unchanged only for the so-called extended products of the “plate” type where the measured thickness $H$ is much smaller than the other dimensions [7, 8]. The term “extended product” itself was first introduced in [8] in order to emphasize the difference with “compact products,” where the measured thickness $H$ is comparable to the other dimensions. Compact BSs are not tested by the traditional impact echo method under real construction conditions. This is due to the following reasons. First, it is impossible to unambiguously determine the required resonant frequency ${{f}_{0}}$ on the spectrum of a compact product against the background of closely spaced numerous frequency peaks determined by the other dimensions [8]. Second, due to a strong influence of the geometric dispersion of the speed of sound in compact TOs, it is necessary to calculate its eigencoefficient $\beta$ for each new product [9]. As a result, the impact echo method is currently being actively developed, however, the development is mainly associated with the creation of new algorithms for processing received information in order to eliminate the stationary effect of the Fourier transform, using window functions or other types of transformations [10, 11], as well as leveling the subjective factor evaluation of the testing result using automated systems and machine learning [12, 13]. The problems of testing the compact products listed above have not found their complete solution [9, 14]. It is for this reason that in this paper the task is to develop a research base for the impact-echo method for testing compact products.

FEATURES AND PROBLEMS OF TESTING COMPACT BUILDING STRUCTURES BY THE IMPACT-ECHO METHOD

The advantage of the impact echo method is not only the ability to test large-sized BSs with a thickness of more than 1.5 m, but also the ease of use, high performance, and relative cheapness of testing devices. That is why the impact-echo method has become widespread in developed countries for testing concrete BSs.

The resonant frequency ${{f}_{0}}$ measured using the impact echo method makes it possible to determine the speed of acoustic vibrations in real concrete BSs using formula (1), provided that the thickness of the concrete product $H$ is known. If the propagation velocity of a longitudinal sound wave in concrete ${{C}_{P}}$ is known in advance, using the echo method, it is easy to determine the thickness of the product $H$,

$$H = \frac{{{{C}_{{PP}}}}}{{2{{f}_{0}}}} = \frac{{\beta {{C}_{P}}}}{{2{{f}_{0}}}}.$$

(3)

In this case, as already noted, the coefficient $\beta$ is constant only for extended products, while for compact products it varies depending on the TO [9]. The resonant frequency ${{f}_{0}}$ is also unambiguously measured only for extended objects. At the same time, the frequency ${{f}_{0}}$ and the correction factor $\beta$ are quite simply determined by modeling in compact TOs with known dimensions. Thus, in [7], using the finite element method, the resonant frequencies and values of the correction coefficients were calculated for “semi-compact” TO where the thickness and width are comparable to each other while the length is much larger than these two dimensions. In [9], using a simulation environment, the coefficients $\beta$ were calculated for TOs that are more complex in configuration, where all three dimensions are comparable to each other. It is obvious that the values of ${{f}_{0}}$ and $\beta$ obtained by modeling do not always coincide with their values for a real concrete product, since the simulation does not take into account the degree of heterogeneity of the concrete structure, the presence and size of aggregates (gravel grains), the unevenness of the edges of a complex configured product, and other BS features. Therefore, there is a need to create experimental methods for determining the resonant frequency ${{f}_{0}}$ and the speed of sound in compact BSs.

MULTICHANNEL MULTIPLICATIVE METHOD FOR DETERMINING THE THICKNESS RESONANCE FREQUENCY IN COMPACT PRODUCTS

The desired resonance frequency ${{f}_{0}}\sim {\text{1/}}H$ is easily determined using the impact echo method in an extended product, whereas it is impossible to detect the desired thickness resonance in the spectrum of a compact product because of the presence of a large number of frequency peaks due to comparable in size dimensions [8]. In this case, the amplitudes of numerous resonant peaks are often comparable with the desired amplitude of the first mode of a longitudinal wave. This effect is illustrated in the spectral characteristics obtained as a result of modeling for compact square-section slabs in Fig. 1.

Fig. 1.

Spectral characteristics of compact slabs 30 cm thick: (a) slab dimensions $150 \times 150 \times 30$ cm ($m = 5$), thickness resonance frequency ${{f}_{0}} \approx 6425$ Hz; (b) slab dimensions $120 \times 120 \times 30$ cm ($m = 4$), thickness resonance frequency ${{f}_{0}} \approx 6500$ Hz; and (c) slab dimensions $90 \times 90 \times 30$ cm ($m = 3$), thickness resonance frequency ${{f}_{0}} \approx 6650$ Hz.

To assess the degree of difference between compact TOs with different dimensions, the concept of “compactness factor,” designated as $m$, was introduced. It is determined by the ratio of the overall dimensions $a = b = D$ to the product thickness $H$. For symmetrical square-section TOs considered in Fig. 1, the coefficients $m = D{\text{/}}H$ are equal to 5, 4, and 3, respectively.

Figure 1a shows the spectrum of a slab with dimensions of $150 \times 150 \times 30$ cm that can still be considered extended ($m = 5$). Therefore, it is possible to unambiguously determine the desired resonant frequency ${{f}_{0}}\sim {\text{1/}}H$ on the frequency response of this plate. As $m$ decreases, the spectral characteristic becomes more complicated and already at $m = 4$ (Fig. 1b) it is quite difficult to unambiguously identify the frequency of the first longitudinal wave mode, which should be used to determine the thickness of the compact product. For $m \leqslant 3$, as can be seen from Fig. 1c, an unambiguous interpretation of the spectrum generally becomes impossible, and the probability of an error in finding the resonance frequency of the first mode of a longitudinal wave increases and reduces the reliability of measurement results. Thus, the simulation results confirm the impossibility of reliably determining the desired thickness resonance frequency and, thereby, determining the correction factor $\beta$ in compact BSs with $m < 5$.

To solve the problem of unambiguously determining the desired resonance frequency ${{f}_{0}}$ in real concrete compact BSs, we proposed a multichannel multiplicative method (RF Patent no. 2354932) that implies the testing to be performed in several points on the BS surface with results being recorded in the memory of the measuring device and with subsequent multiplication of the partial frequency response. Since the peak of the first mode of a longitudinal wave is present in all partial spectra of compact products and the location of this peak is unchanged while the amplitudes of other peaks vary depending on the position of the RT on the surface of the BS, the multiplication of the spectral characteristics leads to the selection of the peak of the desired resonance and to the suppression of other frequency peaks.

Figure 2 shows an example of the implementation of a multiplicative method for determining the resonant frequency in a compact TO with dimensions of $40 \times 40 \times 30$ cm. Figures 2a–2c show the spectral characteristics of the TO obtained by modeling for three positions of the RT located on the surface of the model block near the symmetry axes, as well as the main diagonal. As can be seen from the figures, an unambiguous interpretation of the spectrum in the case of a single measurement is impossible, however, after multiplying these partial characteristics on the final spectrum (Fig. 2d), a resonant peak corresponding to the desired thickness of the compact product is clearly recorded.

Fig. 2.

Results of modeling the multiplicative method for testing compact concrete block with dimensions of $40 \times 40 \times 30$ cm at various positions of the RT (a–c), as well as result of their multiplication (d).

If the impact echo testing method is used to record the experimental frequency response, then such a multichannel method is called the multiplicative impact echo method. If the resonance method is used, then such a method is called, accordingly, the resonance-multiplicative method.

A diagram illustrating the resonant-multiplicative method for testing compact concrete products using four RTs is shown in Fig. 3. It also shows the spectra obtained experimentally at various positions of the RT at the input of the multiplier and the frequency response of the product after multiplication of the partial spectra on which the desired resonant frequency ${{f}_{0}}\sim {\text{1/}}H$ is uniquely determined.

Fig. 3.

Scheme of resonant-multiplicative method for monitoring a compact object.

A feature and advantage of the proposed multiplicative method for determining the resonant frequency is the possibility of its application to plane-parallel compact concrete products with an arbitrary configuration.

CORRELATION METHOD OF SOUND VELOCITY MEASUREMENT IN COMPACT PRODUCTS

Finding the desired resonant frequency ${{f}_{0}}$ in the spectrum of a compact product using the multiplicative impact echo method partially solves the problem of monitoring compact BSs, since now it becomes possible to determine the speed of acoustic vibrations ${{C}_{{PP}}} = 2{{f}_{0}}H$ in compact products with a large thickness $H$. This, in turn, allows solving the problem of determining the strength of concrete by the speed of sound (GOST (State Standard) 17624-2012) both in the process of manufacturing large-sized compact concrete BSs and in the process of operation of building structures in order to predict the accident-free service life of buildings.

However, in some cases, when testing real compact concrete products with a complex structure and nonstandard configuration, the accuracy of determining the resonant frequency ${{f}_{0}}$ using the multiplicative method may not be high enough. Therefore, we have developed another method for experimentally determining the speed ${{C}_{{PP}}}$ in compact complex shaped concrete BSs all dimensions of which are known (RF patent no. 2397487). The essence of this method is illustrated by the example of testing an asymmetric concrete block with dimensions of $80 \times 50 \times 30$ cm. First, the experimental spectral characteristic of a compact concrete block (Fig. 4a, solid line) is taken using one of the eigenfrequency methods, according to which it is rather difficult to establish the desired resonance at frequency ${{f}_{0}} \approx 7500$ kHz. Then, using simulation, the frequency response of the same product is calculated (Fig. 4a, dashed line) at an arbitrarily chosen value of the calculated sound velocity ${{C}_{{{\text{des}}}}} = 3000$ m/s, at which the design frequency response does not coincide with the experimental one. If the value of the velocity of longitudinal vibrations ${{C}_{{{\text{des}}}}}$ taken for calculation corresponded to the real speed ${{C}_{{PP}}}$ of sound in a compact product, then the design and experimental frequency responses would coincide making it possible to determine the exact value of the acoustic wave propagation velocity ${{C}_{{PP}}}$ in the compact concrete product. Therefore, at the next stage, a set of design frequency responses is computed at various values of the calculated speed by scaling the initial calculated characteristic along the frequency axis in the expected speed range (in this example, from 2000 to 5000 m/s) with a step of 10 m/s. So, for example, in order to obtain characteristics corresponding to speeds of 3000, 3010, 3020, and 3030 m/s, it is necessary to multiply the frequency axis of the original characteristic by a factor of 1, 1.0033, 1.0066, and 1.0100, respectively. Then, among all the design frequency responses, the calculated characteristic is found that is most similar to the experimental one (Fig. 4b, dashed line). It is used to determine the speed of sound in concrete ${{C}_{{PP}}} \approx 3765$ m/s.

Fig. 4.

Spectral characteristics of $80 \times 50 \times 30$ cm concrete block: experiment ((a, b), solid line), calculation for speed 3000 m/s ((a), dashed line), calculation with the highest correlation ((b), dashed line). Dependence of cross-correlation on design speed of acoustic vibrations in concrete block (c).

For a more accurate determination of the degree of agreement between the experimental and design characteristics, a dedicated program is used to calculate the cross-correlation coefficient $r$ of the experimental frequency response and all design ones constructed for various values of velocity ${{C}_{{{\text{des}}}}}$. Next, the maximum of the design correlation characteristic $r({{C}_{{{\text{des}}}}})$ is determined, from which the desired velocity of the longitudinal sound wave is found (Fig. 4c). In this compact concrete block ${{C}_{{{\text{des}}\,{\text{max}}}}} = 3765$ m/s.

Thus, the proposed correlation method makes it possible to measure the velocity of a longitudinal acoustic wave in compact products of arbitrary shape. Moreover, the velocity measurement is carried out in the entire volume of the BS, and not in any specific area, let alone at the surface. At the same time, there are no fundamental restrictions on the maximum thickness of the product in the correlation method. The disadvantages of this method include the fact that in order to measure the speed, it is necessary to know all the dimensions of the test product and calculate the frequency response for each new compact object using simulation.

CORRELATION-MULTIPLICATIVE IMPACT-ECHO METHOD FOR MEASURING SOUND VELOCITY IN COMPACT CONCRETE BUILDING STRUCTURES

Unfortunately, in some compact concrete products, it is not always possible to unambiguously determine the maximum on the correlation characteristic $r({{C}_{{{\text{des}}}}})$ due to the fact that the modeling does not take into account the features of the concrete structure and possible surface irregularities of the tested BS. Therefore, in order to improve the accuracy of measuring the speed of sound in concrete, we proposed a correlation-multiplicative method for measuring the speed that uses the impact echo method to determine the experimental frequency responses obtained at various points on the surface of the product, with the partial correlation characteristic $r({{C}_{{{\text{des}}}}})$ calculated for each position of the sensor and with the subsequent multiplication of the set of partial correlation dependences [14].

Figure 5 shows an example of testing a compact nonsymmetrical concrete block measuring $40 \times 30 \times 15$ cm, made of relatively large-sized aggregated concrete (average gravel particle diameter of approcimately 20 mm). Due to the presence of a coarse filler, it is rather difficult to unambiguously determine the speed of sound in concrete by the correlation characteristic $r({{C}_{{{\text{des}}}}})$. Therefore, when monitoring this block, the correlation-multiplicative impact-echo method for measuring velocity was used. For this purpose, we used the Olson Instruments equipment (Fig. 5a) that implements the impact echo method, and spectral characteristics were recorded at four points on the block surface (Fig. 5b). For the same points, the frequency response of the product was constructed by simulation and the cross-correlation functions $r({{C}_{{{\text{des}}}}})$ between the experimental and design spectral characteristics were calculated. Figure 6a shows four dependences $r({{C}_{{{\text{des}}}}})$ for four points on the surface of the tested concrete block. It can be seen from the graphs that the positions of the maxima differ for all correlation dependences making it possible to determine only the approximate value of the speed in the product. To improve the measurement accuracy, multiplicative processing of partial correlation dependences was carried out. The resulting characteristic (Fig. 6b) has one pronounced maximum that uniquely determines the value of the sound wave velocity ${{C}_{{PP}}}$ in concrete ${{C}_{{PP}}} = 3500$ m/s.

Fig. 5.

Testing concrete block by equipment implementing the impact-echo method (a). Scheme of location of the impactor and RT on the surface of the block (b).

Fig. 6.

Dependences of the cross-correlation coefficient of the design and experimental frequency responses on the speed of acoustic vibrations for four positions of sensors on the surface of tested block (a) and the result of their multiplication (b).

In addition to this, a comparative experiment was carried out for measuring the speed of sound in a concrete block $40 \times 40 \times 30$ cm in size during its formation by the proposed correlation-multiplicative method and the standardized (GOST (State Standard) 17624-2012) ultrasonic shadow method. In this case, using the correlation-multiplicative method, the velocity ${{C}_{{PP}}} = \beta {{C}_{P}}$ is calculated, and using the shadow measurement, carried out in our case at a frequency of 100 kHz, specifically the velocity ${{C}_{P}}$ of a longitudinal sound wave is determined. Thus, in order to compare the speed values obtained by different methods, it is necessary to divide the ${{C}_{{PP}}}$ speed by the correction factor $\beta$ corresponding to the $40 \times 40 \times 30$ cm block that compensates for the effect of geometric dispersion. For a given block, $\beta \approx 1.41$, and the ${{C}_{{PP}}}$ velocity is determined by a Lamb wave [9]. Figure 7 shows the set of characteristics $r(C_{{{\text{des}}}}^{*})$ obtained by the correlation-multiplicative method described above on different days in the process of forming a concrete block, where the speed $C_{{{\text{des}}}}^{*}$ is the value reduced to the coefficient $\beta$. This dependence reflects the trend of the tested concrete block gaining strength during its hardening; this is expressed in the growth of the speed of sound measured in it. In turn, the dependence of the change in the velocity of a longitudinal sound wave ${{C}_{P}}$ in the product on the time of concrete molding was determined from the maxima of the partial characteristics $r(C_{{{\text{des}}}}^{*})$ (line 2 of the graph shown in Fig. 8). The graph also shows the dependence obtained as a result of measurements by the through sounding method or the ultrasonic shadow method (line 1 of the graph shown in Fig. 8). The results of measurements by different methods coincide; this confirms the correctness of the proposed correlation-multiplicative impact-echo method for measuring velocity making it possible to increase the accuracy of determining the strength of concrete in large-sized compact building structures.

Fig. 7.

Multiplicative-correlation characteristics obtained on different days in the process of concrete block molding in the course of comparative experiment.

Fig. 8.

Comparison of the results of determining the velocity of a longitudinal sound wave by the correlation-multiplicative impact-echo method and the through sounding method.

CONCLUSIONS

Ultrasonic testing methods do not allow measurements of concrete BSs with a thickness of more than 1.5 m due to the high attenuation of ultrasound. To test such objects, it is necessary to use acoustic methods based on the analysis of the eigenfrequencies of the tested product—the resonance method and the impact echo method considered in this article. The main error of the impact echo method is related to the geometric dispersion of the sound speed that is compensated by the correction factor $\beta$. At the same time, its value is known and constant only for extended products of the “plate” type where the measured thickness is much smaller than the other dimensions. TOs with dimensions that are comparable with each other, called compact products, are not tested by the impact echo method in real construction conditions. This is due to the ambiguity of the frequency response, when the desired thickness resonance cannot be distinguished against the background of multiple frequency peaks, as well as the strong influence of geometric dispersion, due to which it is necessary to calculate the own coefficient $\beta$ for each new compact product.

The article proposes several ways to solve the identified problems of compact product testing. Thus, the described multiplicative impact-echo method makes it possible to experimentally determine the thickness resonance frequency in compact concrete products of arbitrary shape under production conditions. The developed correlation method for measuring the speed of acoustic vibrations makes it possible to solve the problem of determining the strength of concrete from the measured speed both in the process of manufacturing large-sized compact BSs and in the process of operating buildings and structures in order to predict the accident-free service life. In addition, if necessary, it is possible to use the correlation-multiplicative impact echo method proposed in the article for measuring the speed of sound.