Skip to main content
SpringerLink
Log in

On Calculating the Field of a Finite Magnetic Cylinder with an Internal Coaxial Cylindrical Defect

  • ELECTROMAGNETIC METHODS
  • Published:
Russian Journal of Nondestructive Testing Aims and scope Submit manuscript

Abstract

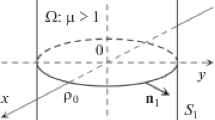
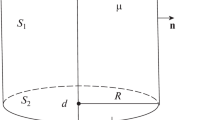
Using a grid method, the direct problem of magnetostatics is numerically solved by calculating the field of a finite cylinder with constant magnetic permeability containing an inclusion in the form of a coaxial cylinder with a different magnetic permeability. The algorithm has been created for an arbitrary external field. In order to assess the reliability and accuracy of the solution, the results were tested using the problems solved exactly. A comparison is also made with the results of the previously solved problem of a finite defect-free cylinder. Coordinate dependences of the components of the resulting field are constructed for various initial data. The program replenishes the library of magnetic control problems and can be used for qualitative comparison with the results of model experiments, as well as for assessing the geometric characteristics of internal defects.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.

Similar content being viewed by others

REFERENCES

  1. Dyakin, V.V. and Kudryashova, O.V., To the calculation of the field of a finite magnetic cylinder, Russ. J. Nondestr. Test., 2019, vol. 55, no. 10, pp. 734–745.

    Article  Google Scholar 

  2. Khizhnyak, N.A., Integral’nye uravneniya makroskopicheskoi elektrodinamiki (Integral Equations of Macroscopic Electrodynamics), Kiev: Naukova Dumka, 1986.

  3. Dyakin, V.V., Matematicheskie osnovy klassicheskoi magnitostatiki (Mathematical Foundations of Classical Magnetostatics), Yekaterinburg: Ural Branch, Russ. Acad. Sci., 2016.

  4. Dyakin, V.V., Kudryashova, O.V., and Raevsky, V.Ya., One approach to the numerical solution of the basic equation of magnetostatics for a finite cylinder in an arbitrary external field, Russ. J. Nondestr. Test., 2021, vol. 57, no. 4, pp. 291–302.

    Article  Google Scholar 

  5. Dyakin, V.V., Raevskii, V.Ya., and Kudryashova, O.V., A flaw in a sphere, Russ. J. Nondestr. Test., 2009, vol. 45, no. 9, pp. 604–615.

    Article  Google Scholar 

  6. Mikhlin, S.G., Kurs matematicheskoi fiziki (Course of Mathematical Physics), Moscow: Nauka, 1968.

  7. Forsyth, J., Malcolm, M., and Mowler, K., Computer Methods for Mathematical Computations, Hoboken, N.J.: Prentice Hall, 1977.

    Google Scholar 

  8. Dyakin, V.V. and Kudryashova, O.V., A flaw in a cylinder, Russ. J. Nondestr. Test., 2012, vol. 48, no. 4, pp. 226–237.

    Article  Google Scholar 

  9. Dyakin, V.V., Kudryashova, O.V., and Raevskii, V.Y., Exact solution of one problem of magnetostatics in bipolar coordinates (continued), Russ. J. Nondestr. Test. 2016, vol. 52, no. 7, pp. 400–408.

    Article  Google Scholar 

Download references

Funding

The work was carried out within the framework of the state-budget topic “Electron.”

Author information

Authors and Affiliations

  1. Mikheev Institute of Metal Physics, Ural Branch, Russian Academy of Sciences, 620137, Yekaterinburg, Russia

    V. V. Dyakin, O. V. Kudryashova & V. Ya. Raevskii

Authors
  1. V. V. Dyakin
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. V. Kudryashova
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. V. Ya. Raevskii
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding authors

Correspondence to V. V. Dyakin, O. V. Kudryashova or V. Ya. Raevskii.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dyakin, V.V., Kudryashova, O.V. & Raevskii, V.Y. On Calculating the Field of a Finite Magnetic Cylinder with an Internal Coaxial Cylindrical Defect. Russ J Nondestruct Test 57, 551–560 (2021). https://doi.org/10.1134/S1061830921070056

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1061830921070056

Keywords:

Search

Navigation