Focusing Properties of Bent Micro-Channel Plates in the X-Ray Range

Abstract

Compact and flexible Micro-Channel Plate (MCP) devices are versatile optical systems suitable to condense and shape intense X-ray beams. Studies on propagation of both soft and hard X-ray radiations through these devices are of continuous interests because of increasing demand of synchrotron radiation X‑ray sources, in particular, to enhance the spot stability and to optimize the beam for specific experiments. In this work synchrotron radiation sources as well as a conventional X-ray tube coupled to polycapillary lenses have been used to characterize the transmission and the angular distribution of thin flat or spherically bent MCPs with different curvature radii. It is shown that the radiation beam from both synchrotron radiation and conventional X-ray sources can be efficiently condensed by thin spherically bent MCPs.

APPENDIX

The framework of the simulation we applied to MCP devices is based on the following assumptions/conditions:

• the propagation of the radiation in a single capillary occurs inside a multilayered cylindrical waveguide described by [30], using the Helmholtz equation for the calculation of waveguide modes;

• the mode amplitudes at the entrance of poly-capillary structures (e.g., MCPs) is calculated using the Kirchhoff–Huygens method;

• the radiation at the exit of the MCP-device is determined by taking into account a finite number of pinholes, considered as independent radiation sources;

• the angular distribution of the X-ray radiation is calculated on the base of the Kirchhoff approximation;

• the radiation pattern of an emitting antenna array has been calculated using the model of the diffraction process at the far field: the Fraunhofer diffraction of waves.

1. The Calculation of the Waveguide Mode Parameters in a Single Capillary

We assumed that X-ray radiation propagates through silicon glass plates in the vacuum inside the holey cylindrical waveguides (pores). Due to several contributions, e.g., technological processes, action of moisture and air, profile of elemental concentrations, surface density, etc. the physical-chemical properties of the transition layer vary with the depth. Since the interaction of long wavelength radiation with a material occurs in a surface layer comparable with the wavelength the permittivity profile vs. depth has to be taken into account. According to our model [31, 32] the transition layer exists as a shell at the inner surface of each microchannel. In this approximation the permittivity changes smoothly between the unitary value in vacuum to $\varepsilon \approx 1 - \delta - i\beta$ in a silicon glass. In addition, we neglect the polarization of X-ray waves ($\left| \varepsilon \right| \cong 1$) and the field is described by the scalar potential $\Psi (r,\varphi ,z) = U(r)\cos m\varphi \exp ( - i\gamma z),$ where $\gamma$ is a complex propagation constant. Actually, the wave function $\Psi (r,\varphi ,z)$ satisfies the Helmholtz equation

$$\Delta \Psi (r,\varphi ,z) + {{k}^{2}}\varepsilon (r)\Psi (r,\varphi ,z) = 0,$$

where Δ is the Laplace operator $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ and $\lambda$ is the radiation wavelength in vacuum. In our approximation the cylindrical transition layer, i.e., the inner shell of the micro-channel, contains N sub-layers or rings in the cross section. The permittivity of each ring is constant and it is determined by the dielectric constant corresponding to the radius of half of the ring. The dispersion equation for the complex value of the propagation constant γ is solved numerically.

2. Calculation of the Mode Amplitude at the Input of Capillaries

We considered the propagation of plane waves and the coordinates z = h, z = –h, corresponding to the entrance and the exit of the waveguide, respectively. The expression below is the plane wave at the entrance of the capillary:

$${{\Psi }^{{ext}}}(x,z) = \exp [i({{k}_{x}}x + {{k}_{z}}z)],$$

((1))

where ${{k}_{x}} = k\sin \varphi ,$${{k}_{z}} = k\cos \varphi ,$$\varphi$ is the grazing angle between the x-ray beam and the wall of the micro-channel. In the plane perpendicular (z = 0) we have

$$\begin{gathered} {{\Psi }^{{ext}}}(x,0) = \exp (i{{k}_{x}}x) = \exp (i{{k}_{x}}r\cos \varphi ) \\ = 2\sum\limits_{m = 0}^\infty {{{\nu }_{m}}{{i}^{m}}{{J}_{m}}({{k}_{x}}r)\cos m\varphi } ,\,\,\,\,{{\nu }_{n}} = \left\{ \begin{gathered} \frac{1}{2},\,\,\,\,n = 0 \hfill \\ 1,\,\,\,\,n \ne 0, \hfill \\ \end{gathered} \right. \\ \end{gathered} $$

((2))

and at the entrance of the capillary, the wave amplitude ${{A}_{{mn}}}(0)$ can be calculated using this integral:

$${{A}_{{mn}}}(0) = \int\limits_0^R {rdr} \int\limits_0^{2\pi } {{{\Psi }^{{ext}}}} (r\cos \varphi ,0){{\Psi }_{{mn}}}(r,\varphi ,0)d\varphi .$$

((3))

Inserting equations (1) and (2) in the equation (3) we obtained the relations:

$${{A}_{{mn}}} = 2\pi {{i}^{m}}I(m,{{\kappa }_{{mn}}},{{k}_{x}},R),$$

$$\begin{gathered} I(m,{{\kappa }_{{mn}}},{{k}_{x}},R) = \int\limits_0^R {r{{J}_{m}}({{k}_{x}}r){{J}_{m}}({{\kappa }_{{mn}}}r)dr} \\ = R\frac{{{{\kappa }_{{mn}}}{{J}_{{m - 1}}}({{\kappa }_{{mn}}}R){{J}_{m}}({{k}_{x}}R) - {{k}_{x}}{{J}_{m}}({{\kappa }_{{mn}}}R){{J}_{{m - 1}}}({{k}_{x}}R)}}{{{{{({{\kappa }_{{mn}}})}}^{2}} - k_{x}^{2}}}, \\ \end{gathered} $$

where ${{\kappa }_{{mn}}}$ is the transverse wave mode number, with index “mn”. The amplitude at the exit of the capillary is

$${{A}_{{mn}}}(h) = {{A}_{{mn}}}(0)\exp ( - \gamma _{{mn}}^{{{{''}}}}h),$$

and $\gamma _{{mn}}^{{{{''}}}} = \operatorname{Im} {{\gamma }_{{mn}}}$ is the attenuation coefficient in the case of $\gamma _{{mn}}^{{{{''}}}} > 0$, and the excitation coefficient for $\gamma _{{mn}}^{{{{''}}}} < 0$. The resultant field in the capillary as calculated in our model is:

$$\begin{gathered} {{U}_{\Sigma }}(r,\varphi ,z) = \sum\limits_{m = 0}^\infty {\sum\limits_{n = 1}^\infty {{{A}_{{mn}}}{{U}_{{mn}}}(r,\varphi ,z)} } \\ = \sum\limits_{m = 0}^\infty {\sum\limits_{n = 1}^\infty {{{A}_{{mn}}}{{J}_{m}}({{\kappa }_{{mn}}}r)\cos m\varphi \exp (i{{\gamma }_{{mn}}}z)} .} \\ \end{gathered} $$

((4))

3. The Angular Distribution of the X-ray Radiation at the Output of MCPs

The radiation field at the output of the MCP can be consider as a double row on spatial harmonics:

$$V(x,y,z) = \sum\limits_{p = - \infty }^\infty {\sum\limits_{q = - \infty }^\infty {{{B}_{{pq}}}\exp [i{{\chi }_{{pq}}}(x,y,z)]} {\kern 1pt} ,} $$

((5))

where B_pq—is the amplitudes of the spatial harmonic and ${{\chi }_{{pq}}}(x,y,z)$ is the phases. To perform calculations only for waves $k < {{\rho }_{{pq}}}$, we have also taken into account the x-ray condition $z \gg \lambda$. The amplitudes of spatial harmonics can be showed with the help of the integral:

$${{B}_{{pq}}} = \int\limits_0^R {rdr} \int\limits_0^{2\pi } {V(x,y,h){{U}_{\Sigma }}(r,\varphi ,h)d\varphi } ,$$

((6))

after introducing Eq.s (4) and (5) in the Eq. (6) we obtained the following relation:

$${{B}_{{pq}}} = 2\pi \sum\limits_{m = 0}^\infty {{{i}^{m}}} \sum\limits_{n = 1}^\infty {{{A}_{{mn}}}I(m,{{\kappa }_{{mn}}},{{\rho }_{{pq}}},R)} .$$

((7))

In the calculation of the Eq. (7), the sum over “n” is considered only for the propagating waveguide modes. The upper limit in the sum over “m” has been selected with numerical experiments and it usually does not exceed three. Each spatial harmonic is a plane wave whose projection of the wave vector on the axis “x, y” holds equal to ${{\alpha }_{p}},{{\beta }_{{qp}}}$, respectively. The angles of the diffraction peaks in the spherical coordinates are defined by

$$\begin{gathered} {{k}_{{x,pq}}} = k\cos {{\varphi }_{{pq}}}\sin {{\theta }_{{pq}}} = {{\alpha }_{p}}, \\ {{k}_{{y,pq}}} = k\sin {{\varphi }_{{pq}}}\sin {{\theta }_{{pq}}} = {{\beta }_{{qp}}}, \\ {{k}_{{z,pq}}} = k\cos {{\theta }_{{pq}}} = {{\gamma }_{{pq}}}. \\ \end{gathered} $$

4. Calculation of X-ray Fraunhofer Diffraction from MCPs at the Far Zone

The radiation pattern of the antenna array is given by the equation:

$$\Phi (\theta ,\varphi ) = {{\Phi }_{a}}(\theta ,\varphi ){{\Phi }_{\nu }}(\theta ,\varphi ),$$

((8))

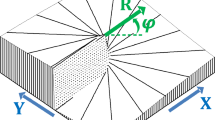
where ${{\Phi }_{a}}(\theta ,\varphi )$ is the radiation pattern of an antenna array made by isotropic emitters, ${{\Phi }_{\nu }}(\theta ,\varphi )$ is the radiation pattern of a single emitter and $\theta ,\varphi$ are the angles of the spherical coordinate system. In this framework, the single emitter is an exit hole of the MCP. The radiation pattern of the planar hexagonal antenna array can be written as:

$${{\Phi }_{a}}(\theta ,\varphi ) = \sum\limits_p {\sum\limits_q {\exp (ik{{\tau }_{{pq}}}),} } $$

((9))

here, ${{\tau }_{{pq}}} = \sin \theta (\cos \varphi {{x}_{{pq}}} + \sin \varphi {{y}_{q}}),{{x}_{{pq}}},{{y}_{q}},$ where ${{x}_{{pq}}} = p{{d}_{x}} + {{y}_{q}}\tan \psi$ and ${{y}_{q}} = q{{d}_{y}}$ are the coordinates of the center of the capillaries; d_x, d_y are the periods of the MCP structure along x and y axes, respectively; and $\psi = 60$ deg for this hexagonal antenna array. The sum in the Eq. (9) is performed using the coordinates of the channels on the surface region of the illuminated MCP. The theory of the excitation of a capillary and of the radiation emitted includes the entire spectrum of waves propagating inside it. Regarding the analysis, the radiation pattern ${{\Phi }_{\nu }}(\theta ,\varphi )$ of a circular hole in an opaque screen can be approximated by the formula:

$${{\Phi }_{\nu }}(\theta ,\varphi ) = {{{{J}_{1}}(kR)} \mathord{\left/ {\vphantom {{{{J}_{1}}(kR)} {kR}}} \right. \kern-0em} {kR}},$$

((10))

where J₁ is the Bessel function, $k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0em} \lambda }$ and R is the radius of the cylindrical capillary.