Skip to main content
SpringerLink
Log in

Identification of Thermal Conductivity Coefficient Using a Given Temperature Field

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

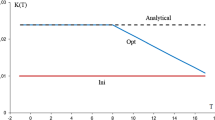
Abstract

The problem of determining the temperature-dependent thermal conductivity coefficient is studied. The study is based on the Dirichlet boundary value problem for the two-dimensional nonstationary heat equation. The cost functional is defined as the rms deviation of the temperature field from experimental data. For the numerical solution of the problem, an algorithm based on the modern fast automatic differentiation technique is proposed. Examples of solving the posed problem are given.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. O. M. Alifanov and V. V. Cherepanov, “Mathematical simulation of high-porosity fibrous materials and determination of their physical properties,” High Temp. 47 (3), 438–447 (2009).

    Article  Google Scholar 

  2. O. M. Alifanov, Inverse Heat Transfer Problems (Mashinostroenie, Moscow, 1988; Springer, Berlin, 2011).

  3. P. N. Vabishchevich and A. Yu. Denisenko, “Numerical methods for solving inverse coefficient problems,” in Methods of Mathematical Modeling and Computational Diagnostics (Mosk. Gos. Univ., Moscow, 1990), pp. 35–45 [in Russian].

    Google Scholar 

  4. A. A. Samarskii and P. N. Vabishchevich, Numerical Methods for Solving Inverse Problems of Mathematical Physics (Nauka, Moscow, 1997; de Gruyter, Berlin, 2007).

  5. A. A. Samarskii and P. N. Vabishchevich, Computational Heat Transfer (Wiley, New York, 1996; Editorial URSS, Moscow, 2003).

  6. V. I. Zubov, “Application of fast automatic differentiation for solving the inverse coefficient problem for the heat equation,” Comput. Math. Math. Phys. 56 (10), 1743–1757 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  7. Yu. G. Evtushenko, Optimization and Fast Automatic Differentiation (Vychisl. Tsentr Ross. Akad. Nauk, Moscow, 2013) [in Russian].

    Google Scholar 

  8. Yu. G. Evtushenko and V. I. Zubov, “Generalized fast automatic differentiation technique,” Comput. Math. Math. Phys. 56 (11), 1819–1833 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  9. Yu. G. Evtushenko, E. S. Zasukhina, and V. I. Zubov, “Numerical optimization of solutions to Burgers’ problems by means of boundary conditions,” Comput. Math. Math. Phys. 37 (12), 1406–1414 (1997).

    MathSciNet  MATH  Google Scholar 

  10. A. F. Albu and V. I. Zubov, “Investigation of the optimal control of metal solidification for a complex-geometry object in a new formulation,” Comput. Math. Math. Phys. 54 (12), 1804–1816 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  11. A. F. Albu and V. I. Zubov, “On the efficient solution of optimal control problems using the fast automatic differentiation approach,” Tr. Inst. Mat. Mekh. Ural. Otd. Ross. Akad. Nauk 21 (4), 20–29 (2015).

    Google Scholar 

  12. A. F. Albu, Y. G. Evtushenko, and V. I. Zubov, “Identification of discontinuous thermal conductivity coefficient using fast automatic differentiation,” Lect. Notes Comput. Sci. 10556, 295–300 (2017).

    Article  Google Scholar 

  13. A. A. Samarskii, The Theory of Difference Schemes (Nauka, Moscow, 1989; Marcel Dekker, New York, 2001).

Download references

ACKNOWLEDGMENTS

This work was supported by the Russian Foundation for Basic Research, project no. 17-07-00493a.

Author information

Authors and Affiliations

  1. Dorodnicyn Computing Center, Federal Research Center “Computer Science and Control,” Russian Academy of Sciences, 119333, Moscow, Russia

    A. F. Albu & V. I. Zubov

  2. Moscow Institute of Physics and Technology (State University), 141700, Dolgoprudnyi, Moscow oblast, Russia

    V. I. Zubov

Authors
  1. A. F. Albu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. I. Zubov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. I. Zubov.

Additional information

Translated by I. Ruzanova

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Albu, A.F., Zubov, V.I. Identification of Thermal Conductivity Coefficient Using a Given Temperature Field. Comput. Math. and Math. Phys. 58, 1585–1599 (2018). https://doi.org/10.1134/S0965542518100032

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542518100032

Keywords:

Search

Navigation