Skip to main content
SpringerLink
Log in

Investigation and improvement of biased Monte Carlo estimates

  • Published:
Computational Mathematics and Mathematical Physics Aims and scope Submit manuscript

Abstract

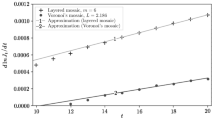
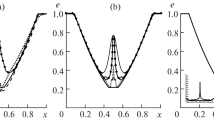
The numerical statistical modeling of the free path of a particle in a collision transport model with allowance for an external force acceleration is based on time stepping. For the corresponding deterministic relative error, a new constructive estimate is obtained, which is used to choose a suitable step size. The standard statistical “local estimates” of the particle flux density are biased because the contributions made by the collisions in a “local ball” of small radius are set to zero to make the variance bounded. Practically effective estimates of the corresponding relative error are presented. Additionally, a uniform optimization of a histogram-type functional estimate of the particle distribution density is presented assuming that the corresponding statistical ensemble is Poisson distributed. It turns out that the deterministic error in optimal (in terms of time complexity) versions of the considered algorithms is close to the statistical error.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. G. A. Mikhailov and A. V. Voitishek, Numerical Statistical Modeling: Monte Carlo Methods (Akademiya, Moscow, 2006) [in Russian].

    Google Scholar 

  2. A. F. Akkerman, Simulation of Trajectories of Charged Particles in Medium (Energoatomizdat, Moscow, 1991) [in Russian].

    Google Scholar 

  3. A. M. Kol’chuzhkin and V. V. Uchaikin, Introduction to the Theory of Transmission of Particles through Matter (Atomizdat, Moscow, 1978) [in Russian].

    Google Scholar 

  4. M. Marchenko, “PARMONC: A software library for massively parallel stochastic simulation,” Lect. Notes Comput. Sci. 6873, 302–315 (2011).

    Article  Google Scholar 

  5. T. A. Averina and G. A. Mikhailov, “Algorithms for exact and approximate statistical simulation of Poisson ensembles,” Comput. Math. Math. Phys. 50(6), 951–962 (2010).

    Article  MathSciNet  Google Scholar 

  6. G. I. Marchuk, G. A. Mikhailov, M. A. Nazaraliev, et al., The Monte Carlo Methods in Atmospheric Optics (Nauka, Novosibirsk, 1976; Springer-Verlag, Berlin, 1980).

    Google Scholar 

  7. G. Z. Lotova, “Modification of the “double local estimate” of the Monte Carlo method in radiation transfer theory,” Russ. J. Numer. Anal. Math. Model. 26(5), 491–500 (2011).

    Article  MATH  MathSciNet  Google Scholar 

  8. G. A. Mikhailov and G. Z. Lotova, “A numerical-statistical estimate for a particle flux with finite variance,” Dokl. Math. 86(3), 743–746 (2012).

    Article  MATH  MathSciNet  Google Scholar 

  9. G. A. Mikhailov, “Total radiation intensity at the center of a sphere exposed to radiation,” Fiz. Atm. Okeana 11(7), 753–754 (1975).

    Google Scholar 

  10. G. A. Mikhailov, Weighted Monte Carlo Methods (Inst. Vychisl. Mat. Mat. Geofiz. Sib. Otd. Ross. Akad. Nauk, Novosibirsk, 2000) [in Russian].

    Google Scholar 

  11. I. A. Ibragimov and R. Z. Khas’minskii, Asymptotic Estimation Theory (Fizmatlit, Moscow, 1979) [in Russian].

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Computational Mathematics and Mathematical Geophysics, Siberian Branch, Russian Academy of Sciences, Novosibirsk, pr. Akademika Lavrent’eva 6, 630090, Russia

    G. Z. Lotova & G. A. Mikhailov

  2. Novosibirsk State University, ul. Pirogova 2, Novosibirsk, 630090, Russia

    G. Z. Lotova & G. A. Mikhailov

Authors
  1. G. Z. Lotova
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. G. A. Mikhailov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to G. Z. Lotova.

Additional information

Original Russian Text © G.Z. Lotova, G.A. Mikhailov, 2015, published in Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 2015, Vol. 55, No. 1, pp. 10–21.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lotova, G.Z., Mikhailov, G.A. Investigation and improvement of biased Monte Carlo estimates. Comput. Math. and Math. Phys. 55, 8–18 (2015). https://doi.org/10.1134/S0965542515010157

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0965542515010157

Keywords

Search

Navigation