Long-Term Energy Demand Forecasting Based on a Systems Analysis

Abstract—

Energy demand forecasting plays a key role in solving the majority of problems connected with determining the economic and energy development prospects. In view of high inertia and capital intensity of energy generation facilities, the changes in the energy consumption structure and rates should be considered for a sufficiently long-term future of no less than 15 years. This adds much difficulty to the development of such forecasts, because it is necessary to take into account the possible results of technological progress in different sectors of the economy and changes in its structure. The suggested approach to energy demand forecasting is based on the systems analysis methods. Energy consumers are disaggregated by economic sectors, country regions, energy carriers, and their utilization areas. As a result, it becomes possible to take into account the possible future technological and structural changes in the economy, its differences in different regions, mutual replacements of energy carriers, and energy saving. The most important feature of the approach is that it involves the separation of economic and energy variables. Economic variables determine the development scales of economic sectors, and energy variables determine the energy consumption intensities in them. The separation of variables helps obtain essentially more accurate forecasts owing to the possibility of taking into account the differences in the variation trends of these variables in the forecast period. For forecasting the economic variables, a nonlinear conditionally dynamic model of interrelations between the economy and energy is used. The energy variables are forecasted on the basis of their links with economic factors, e.g., with cumulative investments in the fixed capital of the considered economic sectors. The discussed approach was implemented as the totality of adaptive simulation models united into the EDFS computing system. The approach was repeatedly and quite successfully used to forecast the energy demand for an up to 10–20-year horizon in solving various problems. The gained experience has demonstrated the correctness of applying the approach for solving long-horizon forecast problems. To illustrate the capacities of the approach, the electric energy demand forecast for the period of up to 2040 for the basic version of the social and economic development of Russia’s economy prepared on the basis of this approach is presented.

Assessments of the future energy requirements, which are drawn up on the basis of forecasting the demands for electricity, heat, and various kinds of fuel, are needed for solving a number of problems connected with developing the country’s and regions’ economy and its effective energy supply [1, 2]. However, the obtaining of such assessments involves significant difficulties, especially for a long horizon. These difficulties stem, in particular, from a great variety of energy consumers and from the market mechanisms forming the energy demand, from a significant number of competing energy carriers and wide possibilities of their mutual replacement, an active energy-saving policy, and uncertainty of the future economic and technological development of the country. For large countries, e.g., Russia, additional difficulties arise in connection with the need for taking into account essential differences of regions in terms of climate, the existing structure of their economies, and economic development rates. As a result, the problem of elaborating energy demand forecasts turns out to be of a high dimension and nonlinear, requiring laborious processing of significant arrays of heterogeneous information and its subsequent reliable storage. Such a problem cannot be solved without developing an appropriate methodology and adequate computation tools.

There are quite a number of methodological approaches and mathematical models for energy demand forecasting [3–11]. Some of them have long been successfully used [12–14], including as part of well-known mathematical models, such as MARKAL [15], MESSAGE [16], GEM [17], NEMS [18], TIMES [19], WEM [20], etc. They differ from one another in the composition of tasks being solved, degree of detail to which the energy consumption structure and the territory considered are described, projection horizon, applied mathematical techniques, information support, etc.

More than a decade ago, specialists of the Energy Research Institute, Russian Academy of Sciences (ERI RAS), proposed an integrated approach to long-horizon forecasting of energy demand [21, 22]. A distinctive feature of that approach was that it involved a sufficiently detailed accounting of the key factors influencing the future energy demand, first of all, the economy development prospects of the country and its regions, and predicted changes in the energy intensity of the manufactured products and services. In application to electricity demand forecasting, this approach was presented in [23].

The discussed approach was implemented as a totality of adaptive simulation models united into the Energy Demand Forecasting System (EDFS) representing a computation system with a distributed architecture [24]. The EDFS system is integrated into the modeling and information complex SCANER (Super Complex for Active Navigation in Energy Research), which was developed at the ERI RAS and used for carrying out fundamental and applied studies [25].

This approach was quite successfully applied several times for energy demand forecasting for an up to 10–20-year horizon in performing various scientific research and applied activities [26–28]. In view of expected serious changes in the energy demand volume and structure, which occur under the influence of the new technological revolution [29] and decarbonization of the world economy, there emerged a need to generalize the experience gained from using the discussed approach and to perform its further development. This first of all relates to more correctly taking into account long-term technological and structural changes in the economy and also its territorial features.

Since energy, i.e., the power industry, is one of the most inertial and capital-intensive economic sectors, quite a long-term future—no less than 15 years—should be considered in determining its development prospects. During this period of time, essential changes in the sectoral and territorial structures of the country’s economy and also in the specific energy intensities in separate economic sectors under the influence of technical progress are unavoidable. Such changes should be taken into consideration in a correct way.

For these reasons, the approach to predicting the demand for energy carriers on the basis of a retrospective trend of energy consumption elasticity with respect to the gross domestic product (GDP) often turns out to be insufficiently correct and yields little information [26]. Such an approach, which is simple in use and requires the minimal scope of information, is quite suitable for application provided that there are no significant structural and technological changes in the economy, large-scale replacement of energy sources, or disturbances connected with economic crises. This, first of all, relates to considering the near future. In other cases, the soundness of the predictions obtained using this approach will always give rise to doubts. Under the conditions of radically transformed structure of the national economy and its energy sector under the effect of powerful technological shifts, the application of such an approach is hardly expedient. Its application is also limited to the development of forecasts for the country as a whole, because a noticeable discrete influence is exerted at the regional level by large investment projects on the side of consumers, which have an effect on the existing trends in the dynamics of the gross domestic product and energy intensities of economic sectors.

DESCRIPTION OF THE METHODOLOGY

The totality of consumers, which form the demand for energy, is a hierarchical system with a heterogeneous internal structure, complex behavior, and a large number of external connections. Energy consumers differ essentially from one another in their properties. It is important to separate among them the specific energy consumption (energy efficiency) for production of goods and rendering of services, and also the possibility of using various energy resources (mutual replacement). Dynamic changes of these properties are caused both by scientific-technical progress and a change in the structure of the goods produced in the considered economic sectors.

It should be noted that rich experience in studying such complex systems with the use of systems analysis methods has been gained [12, 30, 31]. The list of its most important principles as applied to energy includes the following:

1. representing the studied object as a system;

2. structuring the system with identifying its hierarchical levels;

3. determining the properties of system components and establishing links among them;

4. determining external connections;

5. describing the system behavior and its interaction with the environment;

6. determining the system development objectives and boundary conditions;

7. taking into account the system emergence (integrity) property, uncertainties of various nature and the time factor, and competition between different kinds of energy carriers (their mutual replacement at the consumption level), and

8. disaggregating the system to simplify the problem being solved.

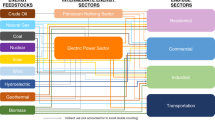
In the discussed approach, the totality of energy consumers is represented as a system formed by economic sectors. They are subdivided into three large groups, which differ considerably from one another in their properties, and which, therefore, require different approaches to energy demand forecasting: end energy use sectors manufacturing goods and rendering services other than energy ones, households, and energy supply sectors providing the consumers with energy carriers in the necessary amounts and with the required quality (Fig. 1). Real sectors along with households form the sector of end energy use.

Fig. 1.

Disaggregation of energy demand by economic sectors.

Disaggregating of the energy demand by the economic sectors is aimed to take into account the nonuniformity of their development and differences in the properties mentioned above. The level of sectoral disaggregation should be sufficient for correctly accounting for the structural and technological shifts in it that may occur in the future.

Real sectors of the economy include production of minerals other than those for energy purposes, processing industries that do not involve reprocessing of fossil fuels, transport (other than pipeline transportation of energy carriers), agriculture, etc. If necessary, they can be disaggregated further. This primarily relates to the processing industry and transport, which are large energy consumers and feature significant internal heterogeneity.

The energy sector is separated in view of its occupying an important place in Russia’s economy and because it features significant export activity. In recent years, it has accounted for approximately 21–25% of the added value produced in the country, more than half of the consumed fuel, and 31–32% of the used electric energy. Approximately half of the fuels produced in the country and their processing products are exported. The following constituent parts of the energy sector are separated:

1. extractive industries specializing in the main kinds of fossil fuel, including the extraction of oil, natural gas, and coal;

2. fuel reprocessing industries;

3. pipeline transportation of natural gas, oil, and petroleum products;

4. generation and distribution of electricity and heat, and

5. production and distribution of hydrogen and other new energy carriers.

The list of main external factors forming the energy demand for the long-term future includes the following:

1. the economic activity of the existing production facilities regulated by market forces;

2. commissioning of new production facilities as a result of implementation of investment projects;

3. technical progress, which influences the energy consumption intensities of the economic sectors and which broadens the composition of the used energy carriers;

4. demographic trends influencing changes in the population size;

5. population incomes, which shape the household needs for energy;

6. external markets determining the amounts of exported energy carriers; and

7. legislative regulation, which is able, as practice shows, to have a significant effect on the energy demand volumes and structure.

In the proposed approach, the energy demand forecast is disaggregated not only by economic sectors but also by energy carriers (energy products), energy carrier utilization areas, and country regions.

The following energy carriers are considered:

1. primary (natural fuels): oil, gas, coal, and biomass (wood, peat, etc.); and

2. secondary (natural fuel and renewable energy source conversion products): motor gasoline, diesel fuel, aviation kerosene, fuel oil, liquefied hydrocarbon gases, coke, solid and liquid biofuels, hydrogen, electricity, and heat (district heating).

Energy demand forecasts for individual economic sectors are developed taking into account territorial differences (in the economy structure, climate, etc.) at the following hierarchical levels: country, 8 federal districts, and 85 Russian Federation administrative entities (Fig. 2). The forecasts are developed according to the “from the top down” method. The mandatory procedure involves coordination of the forecasts developed for adjacent levels. Balancing is performed for all of the considered energy carriers and economic sectors. In performing agreement procedures, priority is given to the upper-level requirements.

Fig. 2.

Scheme of coordinating the forecasts of demands for energy carriers for the country and regions.

For each pth economic sector and tth year, the balance equation linking the demand forecasts for the ith energy carrier for the country E_tpi and for federal districts E_trpi has the form

$${{E}_{{tpi}}} - \sum\limits_r {{{E}_{{trpi}}}} = 0\forall t \in T{\text{,}}\,\,\,\,r \in R{\text{,}}\,\,\,p \in P{\text{,}}\,\,\,i \in I{\text{,}}$$

where T, P, I, and R are the sets of the considered time periods, economic sectors, energy carriers, and regions and r is the region index.

Similar balance equations are written for each federal district for coordinating the forecasts developed for the “federal district”–“administrative entities forming the considered district” system.

Such forecasting scheme turned out to be fairly flexible in nature. It allows the user to limit the prediction scope, if necessary, to the development of forecasts for only two upper levels—of the country and federal districts. This gives the opportunity to make the forecasting process essentially less labor consuming and to weaken the requirements for information support. In some tasks, it is even sufficient to prepare a forecast only for the country as a whole, i.e., only for the upper level alone.

In the general case, the following energy carrier usage fields are distinguished in each economic sector: generation of electricity and heat (stationary energy sources) E^s, meeting of mobile needs (mobile energy sources) E^m, and nonfuel needs, i.e., as raw material, reducing agent, etc. E^nf. For example, natural gas or hydrogen can be used as fuel in stationary and mobile energy sources, and they can also be used as raw materials. Electric energy can be forwarded for meeting the needs of stationary consumers and for driving transport vehicles.

The total demand of the pth economic sector for the ith energy carrier in the tth year is

$${{E}_{{tpi}}} = E_{{tpi}}^{s} + E_{{tpi}}^{m} + E_{{tpi}}^{{nf}}.$$

The consumers have wide possibilities for mutual replacement of energy carriers. This circumstance adds essential difficulty to solving the energy demand forecasting task. The energy replacement problem includes technical and economic aspects and is an optimization one in nature. In particular, in transport vehicles, petroleum products can be displaced by electric energy, natural gas, hydrogen, or biofuel. In metallurgy, hydrogen can be used on certain scales instead of coke and natural gas. The energy-saving problem is of the same multifaceted nature and also requires a search for optimal solutions.

The demand for energy carriers is determined proceeding from the forecasts of social and economic development of the country and regions. In this way, the market mechanisms governing its formation are taken into account, because both the domestic and external markets determine to the main extent the amounts in which nonenergy goods are produced and the values of other macroeconomic factors. Since a significant part of the fuels produced in Russia is exported, the amounts in which they are produced will also depend on the situation in the world markets. The demand for electricity and heat is determined almost completely by the domestic market.

The most important feature of the proposed approach is that it involves separation of the economic and energy variables. The economic (production) variables are extensive in nature and determine the development scales of economic sectors (the products manufactured in individual economic sectors, investments into fixed capital, etc.). They can be expressed in money or natural form. The money form is used for describing sectors manufacturing several kinds of products, and the natural form is used for particular products, for example, oil. The energy variables (energy intensities) characterize the specific consumption of energy for output of products (goods and services).

The separation of economic and energy variables results in essentially more correct energy demand forecasts due to the possibility of taking into account differences in their changes in the forecast period, the more so that such trends are often opposite with respect to each other (the outputs increase, and energy intensities decrease), because they are governed by different factors. In that case, the demand of the pth economic sector for the ith energy carrier in the tth year in the country as a whole can be represented as follows:

$${{E}_{{tpi}}} = {{e}_{{tpi}}}{{V}_{{tp}}},$$

where ${{e}_{{tpi}}}$ is the specific consumption of the ith energy carrier for the product manufactured by the pth sector in the tth year and ${{V}_{{tp}}}$ is the output of products by the pth sector in the tth year.

The demand for each energy carrier for all areas of its use in all of the considered economic sectors is determined in a similar way. The total demand for the ith energy carrier in the tth year E_ti is calculated from the formula

$${{E}_{{ti}}} = \sum\limits_p {\left( {E_{{tpi}}^{s} + E_{{tpi}}^{m} + E_{{tpi}}^{{nf}}} \right)} {\text{.}}$$

Below, the approaches to forecasting the economic and energy variables are discussed.

The developed energy demand forecasting scheme is shown in Fig. 3. The predicted demand for each of the considered energy carriers is the combined result of forecasts for economic sectors, i.e., the sum of the assessments of the demand for energy carrier from all of the separated economic sectors grouped into the sector of end energy use and the energy sector (see Fig. 1).

Fig. 3.

Energy demand forecasting scheme.

In making a forecast for a long horizon, there is always an important problem of how to correctly take into account uncertainties, which stem from inexact knowledge of the conditions under which the economy of the country and its regions will develop in the future and possible technological changes in the economic sectors that determine their energy efficiencies. To handle with uncertainities, both scenario and target approaches can be used. In the first case, a few scenarios are produced, which differ from one another in the combination of external conditions, and external effects are imposed in the second case on the initially determined target trajectory of the social and economic development of the country and regions. The second approach is more informative, but it is more complex in development and subsequent use. Because of this, it has not received wide use. In addition, it can adequately be replaced by the first approach with an extended number of scenarios considered.

The scenario conditions determine the boundaries for the economy development forecasts for the country and its regions. The composition of the conditions is diverse in nature and includes demographic, macroeconomic, and other factors. An important objective pursued by the development of scenarios is to obtain preliminary estimates for development of energy sectors, including the amounts in which fuels are extracted, converted, exported, etc. They are determined with the use of model tools available at the ERI RAS for studying the energy sectors and world energy markets [25]. There is a possibility to update the scenario conditions based on the country’s economic development and energy demand forecasting results.

In the scheme shown in Fig. 3, an important role is given to an analysis of the prospects for the technological development of the world economy and energy sector and also the planned and possible energy saving and mutual energy replacement programs in the economy of Russia. The results of such analysis make it possible to estimate the achieved level of energy consumption efficiency in the considered sectors of Russia’s economy and determine the forecasted annual energy saving and energy replacement rates for them. This information is necessary for making more correct forecasts of energy intensities of these economic sectors.

Based on an analysis of investment projects, discrete disturbances are generated that can have an essential influence on the existing trends in the change of economic indicators and energy intensities of the considered economic sectors. This influence manifests itself especially strongly at the regional level.

FORECASTING THE ECONOMIC INDICATORS AND ENERGY INTENSITIES OF ECONOMIC SECTORS

For forecasting the economic indicators (variables) that are necessary for forecasting the energy demand, various economic and mathematical models can be used, e.g., the classic models of intersectoral input-output balance, equilibrium macroeconomic models (CGE models), or nonlinear models for optimizing the system of product and financial balances in the economic sectors. The nonlinear conditionally dynamic model of interrelations between the economy and energy MENEK (the model of energy in the economy) developed at the ERI RAS, which is used in the scope of the discussed approach to energy demand forecasting [32], relates to the latter type. The MENEK includes the following basic functional units:

1. target constrains;

2. financial balances of economic sectors, state institutions, and households;

3. balances of the production and distribution of goods and services, and economy investment and loan assets, and

4. a monetary and credit system.

The country’s social and economic development forecasts developed by the Ministry of Economic Development of the Russian Federation for a long-term horizon serve as the basis for calculations of the necessary economic indicators. As a rule, these forecasts include only the macroeconomic and some sectoral indicators (the dynamics of agricultural production, key industries, and part of services) general for the country. The regional country development features are not considered in them. Such forecasts are insufficient for determining the future demand for energy by federal districts and the more so by the Russian Federation entities. Therefore, additional economic models are engaged.

First, by using the MENEK, the entire necessary set of economic indicators for the country as a whole is calculated, including the forecasted dynamics of outputs and investments in the economic sectors, added values, incomes of population, etc. After that, the predicted indicators obtained using the MENEK are subjected to two-level territorial detailing. At the first level, they are differentiated by federal districts, after which they serve as specifying values for each federal district and are differentiated by all Russian Federation entities included in the district. The procedure for differentiating the specifying values of indicators has been implemented using the totality of economic and mathematical models describing the economy of the relevant federal districts. These models are identical and differ from one another only in the composition of the Russian Federation entities.

The forecasts of the economic indicators describing the social and economic development of the country and regions with the required degree of detail are developed based on a combination of the following principles:

1. coordinating the future indicators determining the economic development of the country as a whole and its regions;

2. considering the trends that emerged for the past years in the dynamics of the regional structure of the economy, which are determined by changes in the sectoral structure of the economy of regions, and

3. considering large investment projects adopted for implementation that determine essential changes in the sectoral and regional structures of the economy in the forecast period.

In the implementation of these principles, serious difficulties are encountered, for the overcoming of which various methodical techniques have to be applied [33]. The obtained primary data on investment projects are subjected to two-level aggregation for being used in the subsequent calculations [34].

The energy intensities of economic sectors do not remain constant with time. They change under the effect of many factors (technological, structural, etc.). The forecasted dynamics of changes in the energy intensities of economic sectors is proposed to be represented as a base trend with disturbances superposed on them (Fig. 4). The disturbances may be both static (impulse) and dynamic (long-term). Impulse disturbances are determined by large investment projects, which are, as a rule, implemented within quite short periods of time, and dynamic disturbances are determined by long-term measures, first of all, energy saving and mutual energy replacement ones, which were not included in the base trend. With such an approach, it becomes possible to describe the dynamics of change in forecasted energy intensities and, hence, the energy demand, in a more correct manner. This becomes especially important in forecasting the demand at the regional level, for which the contribution of large energy investmtent projects is significant. If the base energy intensity forecast was determined as an interval one, then the final energy intensity forecast estimated taking disturbances into account will also remain an interval one.

Fig. 4.

Forecasting the energy intensity e of economic sectors for the period t. 1, 2—Base and predicted energy intensities; 3—consideration of energy saving (energy replacement); t₀, t₄—beginning and end of the forecast period; t₁–t₂—period of implementing the energy saving (energy replacement program); t₃—investment project implementation.

An important problem is how to correctly describe the interrelation of the economic sector’s energy intensity with a change in the loading of existing production capacities, a decrease of which usually entails a growth of energy intensity, which is connected with conditionally constant energy expenditures in the output of products, i.e., which do not depend on the amounts of production. They can be determined based on retrospective information by linearly approximating the energy consumption in the sector as a function of the amount of manufactured products. Thus, the influence of crisis phenomena in the economy on the energy intensity can be taken into account. As a result, it becomes possible to extend the developed energy consumption forecasting procedure for a stagnating and decaying the economy.

For the economy’s sectors, the forecasted energy intensities on each ith energy carrier are determined by solving the following system of equations:

$$\begin{gathered} {{e}_{{tpi}}} = k_{{tpi}}^{{in{v}}}k_{{tpi}}^{{es}}k_{{tpi}}^{{ex}}k_{{tpi}}^{{pr}}e_{{tpi}}^{o}{\text{;}}\,\,\,\,e_{{tpi}}^{o} = {{f}_{{ep}}}\left( {e_{{pi}}^{{ret}}{\text{,}}~\varphi } \right){\text{;}} \\ k_{{tpi}}^{{in{v}}} = {\text{1}} + \sum\limits_u {\sigma _{{tpu}}^{{in{v}}}\left( {{{e_{{tpiu}}^{{in{v}}}} \mathord{\left/ {\vphantom {{e_{{tpiu}}^{{in{v}}}} {e_{{tpi}}^{o} - {\text{1}}}}} \right. \kern-0em} {e_{{tpi}}^{o} - {\text{1}}}}} \right)} {\text{,}}\;\;u \in {{U}_{p}}{\text{;}} \\ k_{{tpi}}^{{es}} = {{{\text{1}} - \alpha _{{tpi}}^{{es}}} \mathord{\left/ {\vphantom {{{\text{1}} - \alpha _{{tpi}}^{{es}}} {{\text{100}}}}} \right. \kern-0em} {{\text{100}}}}{\text{;}}\,\,\,\,k_{{tpi}}^{{ex}} = {{{\text{1}} - \alpha _{{tpi}}^{{ex}}} \mathord{\left/ {\vphantom {{{\text{1}} - \alpha _{{tpi}}^{{ex}}} {{\text{100}}}}} \right. \kern-0em} {{\text{100}}}}{\text{;}} \\ k_{{tpi}}^{{pr}} = {{\left( {{{\beta }_{{tpi}}}\sigma _{{tp}}^{V} + {\text{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\beta }_{{tpi}}}\sigma _{{tp}}^{V} + {\text{1}}} \right)} {{\text{(}}{{\beta }_{{tpi}}} + {\text{1)}}}}} \right. \kern-0em} {{\text{(}}{{\beta }_{{tpi}}} + {\text{1)}}}}{\text{,}}\,\,\,\,{\text{if}}\,\,\,\,{{V}_{{tp}}} < V_{p}^{*}; \\ k_{{tpi}}^{{pr}} = {\text{1}},\,\,\,\,{\text{if}}\,\,\,\,{{V}_{{tp}}} \geqslant V_{p}^{*}; \\ {{\beta }_{{tpi}}} = {{\sigma _{{tpi}}^{E}} \mathord{\left/ {\vphantom {{\sigma _{{tpi}}^{E}} {\left( {{\text{1}} - \sigma _{{tpi}}^{E}} \right)}}} \right. \kern-0em} {\left( {{\text{1}} - \sigma _{{tpi}}^{E}} \right)}};\,\,\,\,\sigma _{{tpu}}^{{in{v}}} = {{{{V}_{{tpu}}}} \mathord{\left/ {\vphantom {{{{V}_{{tpu}}}} {{{V}_{{tp}}}}}} \right. \kern-0em} {{{V}_{{tp}}}}}; \\ \sigma _{{tp}}^{V} = {{{{V}_{{tp}}}} \mathord{\left/ {\vphantom {{{{V}_{{tp}}}} {V_{p}^{*}}}} \right. \kern-0em} {V_{p}^{*}}};\,\,\,\,\sigma _{{tpi}}^{E} = {{E_{p}^{{con}}} \mathord{\left/ {\vphantom {{E_{p}^{{con}}} {{{E}_{{tpi}}}}}} \right. \kern-0em} {{{E}_{{tpi}}}}}{\text{,}} \\ \end{gathered} $$

where $e_{{tpi}}^{o}$ is the base energy intensity of the pth economic sector on the ith energy carrier that was obtained based on an analysis of the relevant retrospective data $e_{{pi}}^{{ret}}$ and their interrelations with the macroeconomic factors φ; $k_{{tpi}}^{{in{v}}},$ $k_{{tpi}}^{{es}},$ and $k_{{tpi}}^{{ex}}$ are the corrections of the economic sector energy intensity for, respectively, large investment projects, energy-saving measures, and energy replacement; $k_{{tpi}}^{{pr}}$ is a coefficient that takes into account the effect the loading of production capacities has on the economic sector’s energy intensity; $e_{{tpiu}}^{{in{v}}}$ is the energy intensity of the uth investment project by the ith energy carrier; U_p is the set of the investment projects considered in the pth economic sector; $\alpha _{{tpi}}^{{es}}$ and $\alpha _{{tpi}}^{{ex}}$ are the annual energy saving and energy replacement rates in the considered energy sector; $\sigma _{{tpu}}^{{in{v}}}$ is the share of the uth investment project ${{V}_{{tpu}}}$ in the output of products by the pth economic sector; $\sigma _{{tp}}^{V}$ is the decrease in the production capacity load in the pth economic sector with respect to the output of products in the last precrisis year $V_{p}^{*};$ and $\sigma _{{tpi}}^{E}$ is the economic sector’s energy consumption fraction that does not depend on the extent to which the production capacity is loaded, which is defined as the ratio of the constant part of energy consumption by the economic sector $E_{p}^{{con}}$ to its total value.

The disturbances that large investment projects superpose on the economic sector’s base energy intensity are quantitatively determined by the coefficient $k_{{tpi}}^{{in{v}}}.$ This coefficient takes into account the extent to which the energy intensity of the implemented investment projects $e_{{tpiu}}^{{in{v}}}$ differs from the economic sector’s base energy efficiency $e_{{tpi}}^{o}$ and the contribution of these projects into the total output of products by this economic sector $\sigma _{{tpu}}^{{in{v}}}.$ This is an integral indicator, which summarizes the disturbances from all of the considered investment projects implemented in the given economic sector. If the energy intensity of investment projects does not differ from its value averaged over the economic sector, then $k_{{tpi}}^{{in{v}}}$ = 1.

The base energy intensities of economic sectors $e_{{tpi}}^{o}$ are forecasted proceeding from establishing their relationships with macroeconomic indicators. In so doing, the territorial differences that exist between the energy intensities of economic sectors and nonuniformities of changes in these indicators in the future are taken into account. According to the results of our studies, the key role for end energy use economic sectors (see Fig. 1) is played by the relationship between the energy intensity and cumulative investments in the fixed capital of the considered economic sector calculated in commensurable prices [26]. A growth of prices for energy carriers is only a factor motivating improvement of the energy efficiency (i.e., decreasing of its energy intensity). Investments are a means for reaching this objective. Since the energy effect obtained from investments in the form of decreasing the energy intensities is accumulating in nature, cumulative investments (naturally, measured in terms of commensurable prices) should be taken into consideration. The length of the retrospective investment accumulation period is selected individually for each economic sector proceeding from the best approximation of retrospective energy intensity values. The larger the part of investments forwarded for technical modernization of operating production facilities and for extension of production based on the use of new technologies, the stronger the relationship between the energy intensity and investments will be.

As an example, Figure 5 shows the dynamics of change in the electric energy intensity e_el of the processing industry in 2000–2020. The electric energy intensity is defined as the ratio of electric energy consumed by the economic sector to the amount of products manufactured by it in commensurable prices in the corresponding year. A burst of electric energy intensity is clearly seen in the period of economic crisis of 2008–2009 as a consequence of decreased load of production capacities. It is only in 2012 that this indicator returned to its trend trajectory. In 2009, the output of products by the processing industry dropped by a factor of 1.25 in comparison with the precrisis 2007 and restored only in 2012.

Fig. 5.

Processing industry electric energy intensity e_el in the period of 2000–2020.

Figure 6 shows the dependence of the processing industry’s energy intensity on the cumulative investments $K_{{tp}}^{c}$ in this economic sector. With the reported data approximated by the dependence $y = a{{x}^{b}}$ and taking into account the change of production capacity load in the crisis year, the square of the correlation coefficient value is approximately 0.97.

Fig. 6.

Dependence of the processing industry electric energy intensity e_el on cumulative investments (with correction for production capacity loading).

Practical experience has shown that there may be unsatisfactory correlation between the economic sector energy intensity and macroeconomic indicators in some cases. In that case, the forecasted values of economic sector energy intensities can be determined based on their elasticity indicators by the corresponding macroeconomic indicators, e.g., by cumulative investments

$$e_{{tpi}}^{o} = e_{{t - {\text{1}}{\text{,}}pi}}^{o}\left[ {{\text{1}} + L_{{pi}}^{o}\left( {{{K_{{tp}}^{c}} \mathord{\left/ {\vphantom {{K_{{tp}}^{c}} {K_{{t - {\text{1}}{\text{,}}p}}^{c} - {\text{1}}}}} \right. \kern-0em} {K_{{t - {\text{1}}{\text{,}}p}}^{c} - {\text{1}}}}} \right)} \right]{\text{,}}$$

where $L_{{pi}}^{o}$ is the elasticity of the pth economic sector for the ith energy carrier by cumulative investments.

The elasticity indicators are calculated based on retrospective data. In doing so, they can be calculated as the arithmetic mean of annual elasticities for a certain retrospective period n or as the mean elasticity value for the period, which is usually taken as equal to 2–5 years:

$$\begin{gathered} L_{{pi}}^{o} = \frac{{\text{1}}}{n}\sum\limits_{t = {\text{1}}}^n {\left[ {{{\left( {{{e_{{tpi}}^{o}} \mathord{\left/ {\vphantom {{e_{{tpi}}^{o}} {e_{{t - {\text{1}}{\text{,}}pi}}^{o}}}} \right. \kern-0em} {e_{{t - {\text{1}}{\text{,}}pi}}^{o}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{e_{{tpi}}^{o}} \mathord{\left/ {\vphantom {{e_{{tpi}}^{o}} {e_{{t - {\text{1}}{\text{,}}pi}}^{o}}}} \right. \kern-0em} {e_{{t - {\text{1}}{\text{,}}pi}}^{o}}}} \right)} {\left( {{{K_{{tp}}^{c}} \mathord{\left/ {\vphantom {{K_{{tp}}^{c}} {K_{{t - {\text{1}}{\text{,}}p}}^{c}}}} \right. \kern-0em} {K_{{t - {\text{1}}{\text{,}}p}}^{c}}}} \right)}}} \right. \kern-0em} {\left( {{{K_{{tp}}^{c}} \mathord{\left/ {\vphantom {{K_{{tp}}^{c}} {K_{{t - {\text{1}}{\text{,}}p}}^{c}}}} \right. \kern-0em} {K_{{t - {\text{1}}{\text{,}}p}}^{c}}}} \right)}}} \right]} {\text{;}} \\ L_{{pi}}^{o} = {{\left( {{{e_{{tpi}}^{o}} \mathord{\left/ {\vphantom {{e_{{tpi}}^{o}} {e_{{t - n,pi}}^{o}}}} \right. \kern-0em} {e_{{t - n,pi}}^{o}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{e_{{tpi}}^{o}} \mathord{\left/ {\vphantom {{e_{{tpi}}^{o}} {e_{{t - n,pi}}^{o}}}} \right. \kern-0em} {e_{{t - n,pi}}^{o}}}} \right)} {\left( {{{K_{{tp}}^{c}} \mathord{\left/ {\vphantom {{K_{{tp}}^{c}} {K_{{t - n,p}}^{c}}}} \right. \kern-0em} {K_{{t - n,p}}^{c}}}} \right)}}} \right. \kern-0em} {\left( {{{K_{{tp}}^{c}} \mathord{\left/ {\vphantom {{K_{{tp}}^{c}} {K_{{t - n,p}}^{c}}}} \right. \kern-0em} {K_{{t - n,p}}^{c}}}} \right)}}. \\ \end{gathered} $$

For improving the soundness of the selection of the forecasted elasticity values, it is expedient to calculate their sliding mean values for the entire considered retrospective period.

The forecasted household energy intensities are determined from the expression

$${{e}_{{tpi}}} = k_{{tpi}}^{{es}}k_{{tpi}}^{{ex}}e_{{tpi}}^{o}{\text{,}}$$

which uses the same notation as that in the formulas given above.

The base energy intensities of households $e_{{tpi}}^{o}$ are also predicted on the basis of establishing their relationships with macroeconomic indicators. In regard to electricity and heat, there is quite good correlation between them and the living area, and the population incomes. These correlations can be additionally improved by taking the energy carrier price into account.

The suggested approach to energy demand forecasting for economic sectors is integrated in nature. It is essentially a combination of econometric and analytical methods and heuristic procedures. In this way, better soundness of predicted estimates is achieved, which is especially important in making forecasts for a long-term horizon. In our opinion, the limiting horizon for which the application of this approach yields correct results is approximately 15–20 years.

APPROACH APPLICATION EXPERIENCE

As was mentioned above, the proposed approach was applied—several times and quite successfully—for predicting the energy demand in solving various problems. By using this approach, a forecast of the domestic electric energy demand for the period up to 2040 was developed for Russia’s basic socio-economic development scenario. This scenario was drawn up proceeding from the basic version of the Forecast of Social and Economic Development of the Russian Federation for the Period Up to 2036 approved by the Russian Federation Government on November 22, 2018. This scenario was adjusted taking into account the indicators of the country’s midterm economy development forecast (2019) and the crisis phenomena in the world’s and Russia’s economies in 2020 caused by the coronavirus pandemic. The scenario is characterized by the following annual average GDP growth rates in different periods, %, for Russia:

2020–2025	2.5
2026–2030	3.2
2031–2035	3.0
2036–2040	2.9

The processing industry and service businesses, which are the largest economic sectors, will show the outperforming growth rates. Their current share in the total amount of products issued by the economic end energy use sectors exceeds 77% and it will increase to 79% by 2040.

The results from forecasting the electric energy intensities of sectors are given in Table 1. The comparability of the presented electric intensity values is ensured owing to their having been calculated based on the production amounts expressed in constant prices. The average electric energy intensity of all economic real sectors as a whole in 2019 was 4.1 (kW h)/thousand rubles and it is expected to decrease to 3.1 kW h/thousand rubles by 2040, i.e., by a factor of 1.3.

Table 1. Structure of end energy use sectors by issued products and their electric energy intensity

Table 2 gives the forecasted values for the disaggregated processing industry, including the production output structure by sectors expressed in cost and energy intensity terms. The data of Tables 1 and 2 clearly demonstrate that various sectors differ essentially from one another in electric energy intensity by more than 14 times. The consideration of this factor in the case of significant structural changes in the economy is of important significance for obtaining more correct energy demand forecasts.

Table 2. Forecasted indicators of the disaggregated processing industry

The changes in the electric energy intensities of energy supply sectors averaged over the country for the period considered are reflected in Table 3. The highest growth of specific electric energy expenditures is expected in oil extraction and refining, which is connected, first, with expanding the use of secondary and tertiary production methods and, second, with increasing the oil refining depth.

Table 3. Electric energy intensity of energy supply economic sectors

A growth in the specific (per capita) electric energy consumption by households averaged over the country from 1090 (kW h/(person year) in 2019 to 1385 (kW h)/(person year) in 2040 is expected. This is a consequence of the growth of the residential stock and continuing electrification of this sector (extended use of climate control equipment, etc.).

The results from forecasting the domestic demand for electric energy up to 2040 for the base development scenario of Russia’s economy are shown in Fig. 7. Calculations have shown that, with the base scenario, one can expect the growth in the domestic demand for electric energy in Russia from 1110 TW h in 2019 to 1326 TW h in 2035 and 1413 TW h in 2040, i.e., by factors of 1.19 and 1.27, respectively. It should be noted that the existing Energy Strategy of Russia for the Period Up to 2035 approved by the Russian Federation Government Decree no. 1523-r of June 9, 2020, stipulates the increase of electric energy consumption in the country by 2035 up to 1310–1380 (TW h)/year.

Fig. 7.

Forecast of domestic demand for electric energy E_el up to 2040 (for the base scenario).

In Table 4, the domestic energy demand forecast is detailed by economic sectors with separating the energy supply and end energy use sectors. It is expected that the fraction of energy supply sector in the total consumption of electric energy in the country will decrease from 30.8% in 2019 to 27.3% in 2040, which reflects the course for outperforming the growth of nonenergy production facilities in the considered scenario.

Table 4.   Forecast of domestic electric energy demand up to 2040 for the base scenario, (TW h)/year

Table 5 gives the electric energy demand structure in the economic sectors. In the energy supply sector, an increase in the fraction of extractive and processing industries with a decrease in the fraction of energy carrier transportation is forecasted. In the sector of end energy use, it is possible to expect a growth in the fraction of the agriculture and the transport sector. The fraction of households will decrease, which reflects the country’s population size stagnation process with a continuing growth of the economy.

Table 5.   Structure of electric energy demand by economic sectors, %

It should be pointed out that the considered base scenario is free from measures resulting in “new electrification” of the economy, including the development of electric vehicles, the shift for electric heating, mass-scale use of industrial and domestic robots, digital transformation of the society with changeover for the 5G and then 6G standards, production of hydrogen by electrolysis, etc. The implementation of these areas may result in an explosive growth of electric energy demand. The base scenario also does not contain measures determining the policy of active energy saving and mutual energy replacement. Therefore, the forecasted needs for electric energy in it can be considered as a base to which the demand for electric energy from the side of new classes of consumers can be added, and which may also reflect the energy saving results achieved in implementing the energy-saving policy. This is the feature determining the practical value of the base scenario.

Table 6 gives the results obtained from a comparison between the predicted domestic demand for electric energy in the period of 2010–2020 and the actual data. The forecast was made in 2009–2010 based on the statistical information for the period of 1990–2010. Unfavorable, optimistic, and innovative scenarios of the country’s social and economic development were considered. Unfortunately, in reality, the economic development of the country was even poorer than in the worst of the scenarios considered. The actual overall growth in the GDP for the period of 2010–2020 was equal to a factor of 1.12 against the 1.18 stipulated in the unfavorable scenario, and the annual average GDP growth rates were equal to 1.15 and 1.65%, respectively. As a result, the actual domestic electric energy consumption in 2020 (1074 TW h) was essentially lower than that forecasted for the unfavorable scenario (1180 TW h).

Table 6.   Comparison of projections with the actual data for the period of 2010–2020

If the GDP growth predicted in the unfavorable scenario is reduced to its real value, the mismatch between the predicted and actual data on the electric energy consumption by the end of the period will not exceed 4%. With taking into account the production capacities' underload factor, this mismatch will decrease further. This is quite a good result for the difficult period in the development of Russia’s economy. The beginning of this period coincided with the recovery from the heavy economic crisis of 2008–2009. In the middle of this period, there were stagnation phenomena caused by the pressure of sanctions. At the end of this period, a new economic crisis unfolded, which was caused by the coronavirus pandemic. The data given in Table 6 illustrate the importance of the need to carefully elaborate the social and economic development scenarios for the country and regions for correctly forecasting the demand for electric energy and other energy carriers.

CONCLUSIONS

(1) The integrated nature of the approach to forecasting the energy demand in economic sectors, which is based on the systems analysis principles, makes it possible to obtain highly sound predictions, which is especially important in making a forecast for a long-term horizon (up to 15–20 years), in the course of which essential changes may occur in the sectoral and technological structure of the economy. Scientific-technical progress and an active energy and economic policy may become the drivers of such changes. The unfolding decarbonization of the world economy and energy can serve as an example of such changes.

(2) The considered approach gains especial value in the case of using it for elaborating mutually coordinated energy demand forecasts for the country and its regions.

(3) The developed nonlinear conditionally dynamic model of interrelations between the economy and energy (MENEK) is used for producing social and economic development scenarios for the country and regions. This approach has been implemented as a totality of adaptive simulation models united into the EDFS computation system.

(4) The gained experience has shown the adequacy of the approach in applying it to solving various problems connected with determining long-term energy and economic development prospects.