Skip to main content
SpringerLink
Log in

Traveling-wave solution of the Tzitzéica-type equations by using the unified method

  • Research Articles
  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

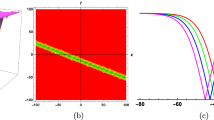
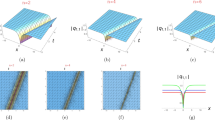
The Tzitzéica equation, the Dodd–Bullough–Mikhailov equation, and the Tzitzéica–Dodd–Bullough equation arise in various branches of science and technology, such as solid state physics, nonlinear dynamics, nonlinear optics, and quantum field theory problems. In this paper, we discuss how to find more general wave solutions of these three nonlinear evolution equations with physical applications using the unified method. The unified method straightforwardly gives many more general solutions with free parameters without the need for extra hardware support. After performing calculations, the graphs of the solutions are plotted using Maple to give insight into the physical structure of the wave solution. Only some selected solutions are plotted to visualize their behavior. Considering the importance of having solutions for nonlinear wave phenomena, we clearly see that the method has many merits and demonstrates a comprehensive application to obtaining solutions in an efficient way. In addition, diverse types of geometrically structured solitons such as an anti-bell-shaped soliton, a flat soliton, a kink, and a singular soliton are produced by using arbitrary parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1.
Fig. 2.
Fig. 3.
Fig. 4.
Fig. 5.
Fig. 6.
Fig. 7.
Fig. 8.

Similar content being viewed by others

References

  1. P. Veeresha, D. G. Prakasha, N. Magesh, A. J. Christopher, and D. U. Sarwe, “Solution for fractional potential KdV and Benjamin equations using the novel technique,” J. Ocean Eng. Sci., 6, 265–275 (2021).

    Article  Google Scholar 

  2. M. H. Bashar, S. M. Y. Arafat, S. M. R. Islam, and M. M. Rahman, “Wave solutions of the couple Drinfel’d–Sokolov–Wilson equation: New wave solutions and free parameters effect,” J. Ocean Eng. Sci. (in press).

    Google Scholar 

  3. W. B. Wang, G. W. Lou, X. M. Shen, and J. Q. Song, “Exact solutions of various physical features for the fifth order potential Bogoyavlenskii–Schiff equation,” Results Phys., 18, 103243, 4 pp. (2020).

    Article  Google Scholar 

  4. A. Alharbi and M. B. Almatrafi, “Numerical investigation of the dispersive long wave equation using an adaptive moving mesh method and its stability,” Results Phys., 16, 102870, 8 pp. (2020).

    Article  Google Scholar 

  5. B. Ghanbari, “New analytical solutions for the Oskolkov-type equations in fluid dynamics via a modified methodology,” Results Phys., 28, 104610, 11 pp. (2021).

    Article  Google Scholar 

  6. M. J. Ablowitz and H. Segur, Solitons and the Inverse Scattering Transform (SIAM Studies in Applied Mathematics, Vol. 4), SIAM, Philadelphia, PA (1981).

    Book  MATH  Google Scholar 

  7. C. Rogers and W. F. Shadwick, Bäcklund Transformations and Their Applications (Mathematics in Science and Engineering, Vol. 161), Academic Press, New York (1982).

    MATH  Google Scholar 

  8. V. B. Matveev and M. A. Salle, Darboux Transform and Solitons, Springer, Berlin (1991).

    Book  MATH  Google Scholar 

  9. R. Hirota, The Direct Method in Soliton Theory (Cambridge Tracts in Mathematics, Vol. 155), Cambridge Univ. Press, Cambridge (2004).

    Book  MATH  Google Scholar 

  10. W. Malfiet, “The tanh method: a tool for solving certain classes of non-linear PDEs,” Math. Methods Appl. Sci., 28, 2031–2035 (2005).

    Article  ADS  MathSciNet  Google Scholar 

  11. A.-M. Wazwaz, Partial Differential Equations and Solitary Waves Theory, Springer, Berlin (2009).

    Book  MATH  Google Scholar 

  12. J.-H. He and X.-H. Wu, “Exp-function method for nonlinear wave equations,” Chaos Solitons Fractals, 30, 700–708 (2006).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. Z. Y. Yan and H. Q. Zhang, “New explicit solitary wave solutions and periodic wave solutions for Whitham–Broer–Kaup equation in shallow water,” Phys. Lett. A, 285, 355–362 (2001).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  14. R. Kumar, R. S. Kaushal, and A. Prasad, “Solitary wave solutions of selective nonlinear diffusion-reaction equations using homogeneous balance method,” Pramana J. Phys., 75, 607–616 (2010).

    Article  ADS  Google Scholar 

  15. Z. Feng and X. Wang, “The first integral method to the two-dimensional Burgers–Korteweg–de Vries equation,” Phys. Lett. A, 308, 173–178 (2003).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. S. T. Demiray and S. Kastak, “MEFM for exact solutions of the \((3+1)\) dimensional KZK equation and \((3+1)\) dimensional JM equation,” Afyon Kocatepe Univ. J. Sci. Eng., 21, 97–105 (2021).

    Google Scholar 

  17. Ö. Kirci, T. Aktürk, and H. Bulut, “Simulation of wave solutions of a mathematical model representing communication signals,” J. Inst. Sci. Tech., 11, 3086–3097 (2021).

    Google Scholar 

  18. S. Akcagil, T. Aydemir, and O. F. Gozukizil, “Comparison between the \((\frac{G'}{G}) \)-expansion method and the extended homogeneous balance method,” New Trends Math. Sci., 3, 223–236 (2015).

    MathSciNet  Google Scholar 

  19. S. Akcagil, T. Aydemir, and O. F. Gozukizil, “Exact travelling wave solutions of nonlinear pseudoparabolic equations by using the \(({G'}/{G})\)-expansion method,” New Trends Math. Sci., 4, 51–66 (2016).

    Article  MathSciNet  Google Scholar 

  20. Ş. Akçagil and T. Aydemir, “Comparison between the \(({G'}/{G})\)-expansion method and the modified extended tanh method,” Open Phys., 14, 88–94 (2016).

    Article  MATH  Google Scholar 

  21. T. Aydemir and Ö. F. Gözükizil, “Exact travelling wave solutions of the Benjamin–Bona–Mahony–Burgers type (BBMB) nonlinear pseudoparabolic equations by using the \((\frac{G'}{G}) \)-expansion method,” Manas J. Eng., 4, 21–37 (2016).

    Google Scholar 

  22. T. Aydemir, Comparison between the \(({G'}/{G})\)-expansion method and the modified extended tanh method and improving unified method (PhD thesis), Sakarya Univ., Turkey (2016).

    Google Scholar 

  23. Ö. F. Gözükizil, Ş. Akçagil, and T. Aydemir, “Unification of all hyperbolic tangent function methods,” Open Phys., 14, 524–541 (2016).

    Article  Google Scholar 

  24. F. Bekhouche, M. Alquran, and I. Komashynska, “Explicit rational solutions for time-space fractional nonlinear equation describing the propagation of bidirectional waves in low-pass electrical lines,” Romanian J. Phys., 66, 114, 18 pp. (2021).

    Google Scholar 

  25. F. Bekhouche and I. Komashynska, “Traveling wave solutions for the space-time fractional \((2+1)\)-dimensional Calogero–Bogoyavlenskii–Schiff equation via two different methods,” Int. J. Math. Comput. Sci., 16, 1729–1744 (2021).

    MathSciNet  MATH  Google Scholar 

  26. H. Ahmad, M. N. Alam, M. A. Rahim, M. F. Alotaibi, and M. Omri, “The unified technique for the nonlinear time-fractional model with the beta-derivative,” Results Phys., 29, 104785, 13 pp. (2021).

    Article  Google Scholar 

  27. M. S. Ullah, H. O. Roshid, M. Z. Ali, A. Biswas, M. Ekici, S. Khan, L. Moraru, A. K. Alzahrani, and M. R. Belic, “Optical soliton polarization with Lakshmanan–Porsezian–Daniel model by unified approach,” Results Phys., 22, 103958 (2021).

    Article  Google Scholar 

  28. Foyjonnesa, N. H. M. Shahen, and M. M. Rahman, “Dispersive solitary wave structures with MI analysis to the unidirectional DGH equation via the unified method,” Partial Differ. Equ. Appl. Math., 6, 100444, 11 pp. (2022).

    Article  Google Scholar 

  29. M. Bilal and J. Ahmad, “Investigation of diverse genres exact soliton solutions to the nonlinear dynamical model via three mathematical methods,” J. Ocean Eng. Sci. (in press).

    Google Scholar 

  30. A. Akbulut and D. Kumar, “Conservation laws and optical solutions of the complex modified Korteweg–de Vries equation,” J. Ocean Eng. Sci. (in press).

    Google Scholar 

  31. M. Bilal, S.-U. Rehman, and J. Ahmad, “Dynamical nonlinear wave structures of the predator-prey model using conformable derivative and its stability analysis,” Pramana J. Phys., 96, 149 (2022).

    Article  ADS  Google Scholar 

  32. S. M. R. Islam, M. H. Bashar, S. M. Y. Arafat, H. Wang, and M. M. Roshid, “Effect of the free parameters on the Biswas–Arshed model with a unified technique,” Chinese J. Phys., 77, 2501–2519 (2022).

    Article  ADS  MathSciNet  Google Scholar 

  33. G. Tzitzéica, “Sur une nouvelle classe de surfaces,” C. R. Acad. Sci. Paris, 150, 955–956 (1910).

    MATH  Google Scholar 

  34. G. Tzitzéica, “Sur une nouvelle classe de surfaces,” C. R. Acad. Sci. Paris, 150, 1227–1229 (1910).

    MATH  Google Scholar 

  35. R. K. Dodd and R. K. Bullough, “Polynomial conserved densities for the sine-Gordon equations,” Proc. Roy. Soc. London Ser. A, 352, 481–503 (1977).

    Article  ADS  MathSciNet  Google Scholar 

  36. A. M. Wazwaz, “The tanh method: solitons and periodic solutions for the Dodd–Bullough–Mikhailov and the Tzitzéica–Dodd–Bullough equations,” Chaos Solitons Fractals, 25, 55–63 (2005).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  37. R. Abazari, “The the \(\bigl(\frac{G'}{G}\bigr)\)-expansion method for Tzitzéica type nonlinear evolution equations,” Math. Comput. Modelling, 52, 1834–1845 (2010).

    Article  MathSciNet  MATH  Google Scholar 

  38. K. Khan and M. A. Akbar, “Exact and solitary wave solutions for the Tzitzéica–Dodd–Bullough and the modifed KdV–Zakharov–Kuznetsov equations usingthe modifed simple equation method,” Ain Shams Eng. J., 4, 903–909 (2013).

    Article  Google Scholar 

  39. H. Durur, A. Yokuş, and K. A. Abro, “Computational and traveling wave analysis of Tzitzéica and Dodd–Bullough–Mikhailov equations: An exact and analytical study,” Nonlinear Eng., 10, 272–281 (2021).

    Article  ADS  Google Scholar 

  40. S. Akcagil and T. Aydemir, “A new application of the unified method,” New Trends Math. Sci., 6, 185–199 (2018).

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Economics and Administrative Sciences, Yalova University, Yalova, Turkey

    T. Aydemir

Authors
  1. T. Aydemir
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. Aydemir.

Ethics declarations

The author declares no conflicts of interest.

Additional information

Prepared from an English manuscript submitted by the author; for the Russian version, see Teoreticheskaya i Matematicheskaya Fizika, 2023, Vol. 216, pp. 43–62 https://doi.org/10.4213/tmf10430.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Aydemir, T. Traveling-wave solution of the Tzitzéica-type equations by using the unified method. Theor Math Phys 216, 944–960 (2023). https://doi.org/10.1134/S0040577923070048

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0040577923070048

Keywords

Search

Navigation