Skip to main content
SpringerLink
Log in

Similarity reductions of peakon equations: the \(b\)-family

  • Research Articles
  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

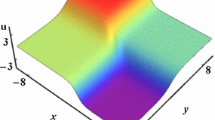
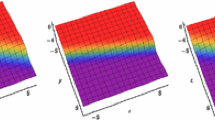
The \(b\)-family is a one-parameter family of Hamiltonian partial differential equations of nonevolutionary type, which arises in shallow water wave theory. It admits a variety of solutions, including the celebrated peakons, which are weak solutions in the form of peaked solitons with a discontinuous first derivative at the peaks, as well as other interesting solutions that have been obtained in exact form and/or numerically. In each of the special cases \(b=2\) and \(b=3\) (the Camassa–Holm and Degasperis–Procesi equations, respectively), the equation is completely integrable, in the sense that it admits a Lax pair and an infinite hierarchy of commuting local symmetries, but for other values of the parameter \(b\) it is nonintegrable. After a discussion of traveling waves via the use of a reciprocal transformation, which reduces to a hodograph transformation at the level of the ordinary differential equation satisfied by these solutions, we apply the same technique to the scaling similarity solutions of the \(b\)-family and show that when \(b=2\) or \(b=3\), this similarity reduction is related by a hodograph transformation to particular cases of the Painlevé III equation, while for all other choices of \(b\) the resulting ordinary differential equation is not of Painlevé type.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. A. Degasperis, D. D. Holm, and A. Hone, “A new integrable equation with peakon solutions,” Theoret. and Math. Phys., 133, 1463–1474 (2002).

    Article  MathSciNet  Google Scholar 

  2. A. Degasperis, D. D. Holm, and A. N. W. Hone, “Integrable and non-integrable equations with peakons,” in: Nonlinear Physics. Theory and Experiment II (Gallipoli, Italy, 27 June – 6 July 2002, M. J. Ablowitz, M. Boiti, F. Pempinelli, and B. Prinari, eds.), World Sci., Singapore (2003), pp. 37–43; arXiv: nlin/0209008.

    Chapter  MATH  Google Scholar 

  3. A. Degasperis and M. Procesi, “Asymptotic integrability,” in: Symmetry and Perturbation Theory (Rome, Italy, December 16–22, 1998, A. Degasperis and G. Gaeta, eds.), World Sci., Singapore (1999), pp. 23–37.

    Google Scholar 

  4. R. Camassa and D. D. Holm, “An integrable shallow water equation with peaked solitons,” Phys. Rev. Lett., 71, 1661–1664 (1993).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  5. B. Fuchssteiner and A. S. Fokas, “Symplectic structures, their Bäcklund transformation and hereditary symmetries,” Phys. D, 4, 47–66 (1981).

    Article  MathSciNet  MATH  Google Scholar 

  6. H. R. Dullin, G. A. Gottwald, and D. D. Holm, “Camassa–Holm, Korteweg–de Vries-5 and other asymptotically equivalent equations for shallow water waves,” Fluid Dynam. Res., 33, 73–95 (2003).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  7. H. R. Dullin, G. A. Gottwald, and D. D. Holm, “On asymptotically equivalent shallow water wave equations,” Phys. D, 190, 1–14 (2004).

    Article  MathSciNet  MATH  Google Scholar 

  8. A. Constantine and D. Lannes, “The hydrodynamical relevance of the Camassa–Holm and Degasperis–Procesi equation,” Arch. Ration. Mech. Anal., 192, 165–186 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  9. R. I. Ivanov, “Water waves and integrability,” Philos. Trans. R. Soc. London Ser. A, 365, 2267–2280 (2007); arXiv: 0707.1839.

    ADS  MathSciNet  MATH  Google Scholar 

  10. D. D. Holm and A. N. W. Hone, “A class of equations with peakon and pulson solutions (with an Appendix by Harry Braden and John Byatt-Smith),” J. Nonlinear Math. Phys., 12, suppl. 1, 380–394 (2005).

    Article  ADS  MATH  Google Scholar 

  11. A. Chertock, J.-G. Liu, and T. Pendleton, “Convergence of a particle method and global weak solutions of a family of evolutionary PDEs,” SIAM J. Numer. Anal., 50, 1–21 (2012).

    Article  MathSciNet  MATH  Google Scholar 

  12. R. Beals, D. H. Sattinger, and J. Szmigielski, “Multi-peakons and a theorem of Stieltjes,” Inverse Problems, 15, L1–L4 (1999).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  13. R. Beals, D. H. Sattinger, J. Szmigielski, “Multipeakons and the classical moment problem,” Adv. Math., 154, 229–257 (2000).

    Article  MathSciNet  MATH  Google Scholar 

  14. H. Lundmark and J. Szmigielski, “Multi-peakon solutions of the Degasperis–Procesi equation,” Inverse Problems, 19, 1241–1245 (2003); arXiv: nlin/0503033.

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. H. Lundmark and J. Szmigielski, “Degasperis–Procesi peakons and the discrete cubic string,” Internat. Math. Res. Rap., 2005, 53–116 (2005).

    MathSciNet  MATH  Google Scholar 

  16. A. N. W. Hone and J. P. Wang, “Prolongation algebras and Hamiltonian operators for peakon equations,” Inverse Problems, 19, 129–145 (2003).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. A. N. W. Hone and S. Lafortune, “Stability of stationary solutions for nonintegrable peakon equations,” Phys. D, 269, 28–36 (2014).

    Article  MathSciNet  MATH  Google Scholar 

  18. J. Escher and B. Kolev, “The Degasperis–Procesi equation as a non-metric Euler equation,” Math. Z., 269, 1137–1153 (2011).

    Article  MathSciNet  MATH  Google Scholar 

  19. G. Misiołek, “A shallow water equation as a geodesic flow on the Bott–Virasoro group,” J. Geom. Phys., 24, 203–208 (1998).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  20. A. N. W. Hone, “Painlevé tests, singularity structure and integrability,” in: Integrability (Lecture Notes in Physics, Vol. 767, A. V. Mikhailov, ed.), Springer, Berlin (2009), pp. 245–277.

    Chapter  MATH  Google Scholar 

  21. A. V. Mikhailov and V. S. Novikov, “Perturbative symmetry approach,” J. Phys. A: Math. Gen., 35, 4775–4790 (2002).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  22. V. P. Ermakov, “Second-order differential equations: Conditions of complete integrability,” Appl. Anal. Discrete Math., 2, 123–145 (2008).

    Article  MathSciNet  MATH  Google Scholar 

  23. D. D. Holm and M. F. Staley, “Nonlinear balance and exchange of stability in dynamics of solitons, peakons, ramps/cliffs and leftons in a \(1+1\) nonlinear evolutionary PDE,” Phys. Lett. A, 308, 437–444 (2003); arXiv: nlin/0203007.

    Article  ADS  MathSciNet  MATH  Google Scholar 

  24. D. D. Holm and M. F. Staley, “Wave structure and nonlinear balances in a family of evolutionary PDEs,” SIAM J. Appl. Dyn. Syst., 2, 323–380 (2003).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  25. T. Tao, “Why are solitons stable?,” Bull. Amer. Math. Soc. (N. S.), 46, 1–33 (2009).

    Article  MathSciNet  MATH  Google Scholar 

  26. H. Inci, “On the well-posedness of the Holm–Staley \(b\)-family of equations,” J. Nonlinear Math. Phys., 23, 213–233 (2016).

    Article  MathSciNet  MATH  Google Scholar 

  27. L. Molinet, “A rigidity result for the Holm–Staley \(b\)-family of equations with application to the asymptotic stability of the Degasperis–Procesi peakon,” Nonlinear Anal. Real World Appl., 50, 675–705 (2019).

    Article  MathSciNet  MATH  Google Scholar 

  28. E. G. Charalampidis, R. Parker, P. G. Kevrekidis, and S. Lafortune, “The stability of the \(b\)-family of peakon equations,” arXiv: 2012.13019.

  29. S. Lafortune and D. E. Pelinovsky, “Spectral instability of peakons in the \(b\)-family of the Camassa–Holm equations,” arXiv: 2105.13196.

  30. A. N. W. Hone, “The associated Camassa–Holm equation and the KdV equation,” J. Phys. A: Math. Gen., 32, L307–L314 (1999).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. R. Camassa, D. D. Holm, and J. M. Hyman, “A new integrable shallow water equation,” Adv. Appl. Mech., 31, 1–33 (1994).

    Article  MATH  Google Scholar 

  32. Y. Matsuno, “The \(N\)-soliton solution of the Degasperis–Procesi equation,” Inverse Problems, 21, 2085–2101 (2005).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  33. Y. A. Li and P. J. Olver, “Convergence of solitary-wave solutions in a perturbed bi-Hamiltonian dynamical system I. Compactions and peakons,” Discrete Contin. Dynam. Syst., 3, 419–432 (1997).

    Article  MATH  Google Scholar 

  34. A. Constantin and H. P. McKean, “A shallow water equation on the circle,” Comm. Pure Appl. Math., 52, 949–982 (1999).

    Article  MathSciNet  MATH  Google Scholar 

  35. K. Okamoto, “On the \(\tau\)-function of the Painlevé equations,” Phys. D, 2, 525–535 (1981).

    Article  MathSciNet  MATH  Google Scholar 

  36. A. E. Milne, P. A. Clarkson, and A. P. Bassom, “Bäcklund transformations and solution hierarchies for the third Painlevé equation,” Stud. Appl. Math., 98, 139–194 (1997).

    Article  MathSciNet  MATH  Google Scholar 

  37. P. A. Clarkson, “The third Painlevé equation and associated special polynomial,” J. Phys. A: Math. Gen., 36, 9507–9532 (2003).

    Article  ADS  MATH  Google Scholar 

  38. P. J. Forrester and N. S. Witte, “Application of the \(\tau\)-function theory of Painlevé equations to random matrices: \(\rm P_\mathrm{V}\), \(\rm P_\mathrm{III}\), the LUE, JUE, and CUE,” Comm. Pure Appl. Math., 55, 679–727 (2002).

    Article  MathSciNet  MATH  Google Scholar 

  39. L. E. Barnes, Integrable and non-integrable equations with peaked soliton solutions, (Ph.D. thesis), University of Kent (2020).

    Google Scholar 

  40. A. S. Fokas, “On a class of physically important integrable equations,” Phys. D, 87, 145–150 (1995).

    Article  MathSciNet  MATH  Google Scholar 

  41. P. J. Olver and P. Rosenau, “Tri-Hamiltonian duality between solitons and solitary-wave solutions having compact support,” Phys. Rev. E, 53, 1900–1906 (1996).

    Article  ADS  MathSciNet  Google Scholar 

  42. Z. Qiao, “A new integrable equation with cuspons and W/M-shape-peaks solitons,” J. Math. Phys., 47, 112701, 9 pp. (2006).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  43. V. Novikov, “Generalizations of the Camassa–Holm equation,” J. Phys. A: Math. Theor., 42, 342002, 14 pp. (2009).

    Article  MathSciNet  MATH  Google Scholar 

Download references

Funding

L. E. Barnes was supported by a PhD studentship from SMSAS, Kent. The research of A. N. W. Hone was supported by Fellowship EP/M004333/1 from the Engineering & Physical Sciences Research Council, UK, and is currently funded by grant IEC\R3\193024 from the Royal Society.

Author information

Authors and Affiliations

  1. School of Mathematics, Statistics and Actuarial Science, University of Kent, Canterbury, United Kingdom

    L. E. Barnes & A. N. W. Hone

Authors
  1. L. E. Barnes
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. N. W. Hone
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. N. W. Hone.

Ethics declarations

The authors declare no conflicts of interest.

Additional information

Prepared from an English manuscript submitted by the author; for the Russian version, see Teoreticheskaya i Matematicheskaya Fizika, 2022, Vol. 212, pp. 303–324 https://doi.org/10.4213/tmf10238.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Barnes, L.E., Hone, A.N.W. Similarity reductions of peakon equations: the \(b\)-family. Theor Math Phys 212, 1149–1167 (2022). https://doi.org/10.1134/S0040577922080104

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0040577922080104

Keywords

Search

Navigation