Skip to main content
SpringerLink
Log in

Solitons in the Domain Structure of the Ferromagnet

  • Published:
Theoretical and Mathematical Physics Aims and scope Submit manuscript

Abstract

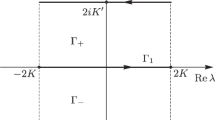
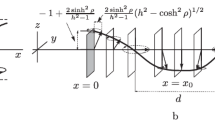
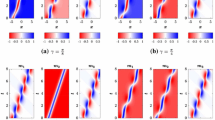
By the method of dressing on a torus, we obtain and study solutions of the Landau–Lifshitz equation, which describe solitons in the stripe domain structure of the easy-axis ferromagnet. A specific feature of these solitons is that they are directly related to the domain structure: they induce translations and local oscillations of the domains. We find integrals of motion stabilizing the solitons on the background of the structure.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. E. K. Sklyanin, “On complete integrability of the Landau–Lifshitz equation [in Russian],” Preprint No. 79-E-3, LOMI, Leningrad (1979).

    MATH  Google Scholar 

  2. A. E. Borovik and V. N. Robuk, “Linear pseudopotentials and conservation laws for the Landau–Lifshits equation describing the nonlinear dynamics of a ferromagnet with uniaxial anisotropy,” Theor. Math. Phys., 46, 242–248 (1981).

    Article  Google Scholar 

  3. A. M. Kosevich, B. A. Ivanov, and A. S. Kovalev, Nonlinear Magnetization Waves: Dynamical and Topological Solitons [in Russian], Naukova Dumka, Kiev (1983).

    Google Scholar 

  4. A. E. Borovik, S. Klama, and S. I. Kulinich, “Integration of the Landau–Lifshitz equation with preferred-axis anisotropy by the method of the inverse scattering problem,” Phys. D, 32, 107–134 (1988).

    Article  MathSciNet  MATH  Google Scholar 

  5. A. B. Borisov and V. V. Kiselev, Quasi-One-Dimensional Magnetic Solitons [in Russian], Fizmatlit, Moscow (2014).

    Google Scholar 

  6. R. F. Bikbaev, A. I. Bobenko, and A. R. Its, “Landau–Lifstits equation: Theory of exact solutions II [in Russian],” Preprint DonFTI-84-7(82), Donetskii Fiz.-Tekhn. Inst. AN-USSR, Donetsk (1984).

    Google Scholar 

  7. R. F. Bikbaev, A. I. Bobenko, and A. R. Its, “On finite-zone integration of the Landau–Lifshits equation,” Sov. Math. Dokl., 28, 512–516 (1983).

    MATH  Google Scholar 

  8. Yu. A. Mitropol’skii, N. N. Bogolyubov Jr., A. K. Prikarpatskii, and V. G. Samoilenko, Integrable Dynamical Systems: Spectral and Differential-Geometric Aspects [in Russian], Naukova Dumka, Kiev (1987).

    Google Scholar 

  9. A. I. Bobenko, “Real algebrogeometric solutions of the Landau–Lifshits equation in Prym theta functions,” Funct. Anal. Appl., 19, 5–17 (1985).

    Article  MATH  Google Scholar 

  10. H. Bateman and E. Erdelyi, Higher Transcendental Functions, Vol. 3, McGraw-Hill, New York (1955).

    MATH  Google Scholar 

  11. P. F. Byrd and M. D. Friedman, Handbook of Elliptic Integrals for Engineers and Scientists, Springer, Berlin (1971).

    Book  MATH  Google Scholar 

  12. V. V. Kiselev and A. A. Raskovalov, “Nonlinear dynamics of a quasi-one-dimensional helical structure,” Theor. Math. Phys., 173, 1565–1586 (2012).

    Article  MATH  Google Scholar 

  13. V. V. Kiselev and A. A. Rascovalov, “Nonlinear collective excitations in helical magnetic structures,” Phys. Metals Metallogr., 113, 1114–1126 (2012).

    Article  ADS  Google Scholar 

  14. V. V. Kiselev and A. A. Raskovalov, “Solitons and nonlinear waves in the spiral magnetic structures,” Chaos Solitons Fractals, 84, 88–103 (2016).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. A. V. Mikhailov, “The Landau–Lifschitz equation and the Riemann boundary problem on a torus,” Phys. Lett., 92, 51–55 (1982).

    Article  MathSciNet  Google Scholar 

  16. A. B. Borisov and V. V. Kiselev, “Many-soliton solutions of asymmetric chiral SU(2) and SL(2, R) theories (d = 1),” Theor. Math. Phys., 54, 160–167 (1983).

    Article  Google Scholar 

  17. A. B. Borisov, “The Hilbert problem for matrices and a new class of integrable equations,” Lett. Math. Phys., 7, 195–199 (1983).

    Article  ADS  MathSciNet  MATH  Google Scholar 

  18. N. I. Akhiezer, Elements of the Theory of Elliptic Functions [in Russian], Nauka, Moscow (1970); English transl. (Transl. Math. Monogr., Vol. 79), Amer. Math. Soc., Providence, R. I. (1990).

    Book  MATH  Google Scholar 

  19. V. V. Kiselev and A. A. Raskovalov, “Interaction of a breather with a magnetization wave in a ferromagnet with light-axis anisotropy,” Theor. Math. Phys., 163, 479–495 (2010).

    Article  MATH  Google Scholar 

  20. V. V. Kiselev and A. A. Raskovalov, “Forced motion of solitary domains and domain walls in the field of a nonlinear magnetization wave,” Phys. Metals Metallogr., 109, 585–598 (2010).

    Article  ADS  Google Scholar 

  21. V. V. Kiselev and A. A. Raskovalov, “Forced motion of breathers and domain boundaries against the background of nonlinear magnetization wave,” Chaos Solitons Fractals, 45, 1551–1565 (2012).

    Article  ADS  Google Scholar 

  22. V. E. Zakharov, S. V. Manakov, S. P. Novikov and L. P. Pitaevskii, Theory of Solitons: The Inverse Scattering Method [in Russian], Nauka, Moscow (1980); English transl., Plenum, New York (1984).

    MATH  Google Scholar 

  23. L. A. Takhtadzhyan and L. D. Faddeev, Hamiltonian Methods in the Theory of Solitons [in Russian], Nauka, Moscow (1986); English transl., Springer, Berlin (2007).

    MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mikheev Institute of Metal Physics, Ural Branch, RAS, Ekaterinburg, Russia

    V. V. Kiselev & A. A. Raskovalov

  2. Yeltsin Ural Federal University, Ekaterinburg, Russia

    V. V. Kiselev & A. A. Raskovalov

Authors
  1. V. V. Kiselev
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. A. A. Raskovalov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to V. V. Kiselev.

Additional information

This research was performed within the State Assignment of the Federal Agency for Scientific Organizations (Topic “Kvant,” No. 01201463332 (AAAA-A18-118020190095-4)).

Translated from Teoreticheskaya i Matematicheskaya Fizika, Vol. 197, No. 1, pp. 89–107, October, 2018.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kiselev, V.V., Raskovalov, A.A. Solitons in the Domain Structure of the Ferromagnet. Theor Math Phys 197, 1469–1486 (2018). https://doi.org/10.1134/S0040577918100057

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S0040577918100057

Keywords

Search

Navigation