Abstract
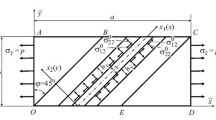
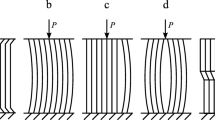
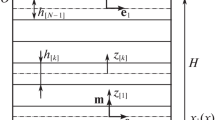
This paper proposes a refined formulation of linearized problems of internal nonuniformly scaled flat buckling modes of a rigid lamina consisting of fibers and fiber bundles with allowance for their interaction with the surrounding matrix. Fibers are the structural elements of fibrous composites and in a prebuckling (unperturbed) state under the action of shear stresses and tensile (compression) stresses in the transverse direction. The problems are formulated using equations constructed by reducing the version of geometrically nonlinear equations of the elasticity theory to one-dimensional equations of the theory of rectilinear rods. These equations are based on the use of the refined Timoshenko shear model with allowance for tension-compression strains in the transverse direction for the rigid lamina and the transverse-soft layer model with immobile boundary planes in a perturbed state for the epoxy layers. It is shown that loading samples with a structure is accompanied by constant changes in the composite structure due to implementation and alternation of the internal buckling modes with a varying wave formation parameter. This particularly allows explaining the changing of the effective shear modulus of the fibrous composite with increasing shear strains.
Similar content being viewed by others
References
A. N. Guz, Stability of Elastic Bodies under Uniform Compression (Naukova Dumka, Kiev, 1973) [in Russian].
V. V. Bolotin and Yu. N. Novichkov, Mechanics of Multilayered Structures (Mashinostroenie, Moscow, 1980) [in Russian].
A. N. Polilov, Studies on the Mechanics of Composites (Fizmatlit, Moscow, 2015) [in Russian].
M. A. Alimov, A. M. Dumanskii, and A. A. Radchenko, “Analysis of Strain Nonlinearity Under Uniaxial Tension of Cross Ply Stacking Sequence Carbon Fiber,” Probl. Mashinost. Nadezh. Mashin, No. 2, 39–44 (2012).
V. N. Paimushin, V. A. Firsov, and S. A. Kholmogorov, “Nonlinear Behavior of a Fibrous Composite Based on a Carbon Fiber Under Shear,” in Dynamics and Engineering Problems of Structure Mechanics and Continuous Media, Proc. of the 22nd Int. Symp. Named After A. G. Gorshkov, Moscow, February, 15–19, 2016 (TR-print, Moscow, 2016), Vol. 1.
V. N. Paimushin, D. V. Tarlakovskii, and S. A. Kholmogorov, “Nonclassical Bucking Mode and Fracture of Composite Test Samples in the Case of Three-Point Bending,” Uchen. Zap. Kazan. Cos. Univ., Ser. Fiz.-Mat. Nauki 158 (3), 350–375 (2016).
V. N. Paimushin, S. A. Kholmogorov, and I. B. Badriev, “Theoretical and Experimental Investigations of the Formation Mechanisms of Residual Deformations of Fibrous Layered Structure Composites,” MATEC Web Conf. 129, 1–5 (2017).
V. N. Paimushin and S. A. Kholmogorov, “Physical-Mechanical Properties of a Fiber-Reinforced Composite Based on an ELUR-P Carbon Tape and XT-118 Binder,” Mech. Compos. Mater. 54 (1), 2–12 (2018).
V. N. Paimushin, S. A. Kholmogorov, and R. K. Gazizullin, “Mechanics of Unidirectional Fiber-Reinforced Composites: Buckling Modes and Failure Under Compression Along Fibers,” Mech. Compos. Mater. 53 (6), 737–752 (2017).
B. W. Rosen, “Mechanics of Composite Strengthening,” in Fiber Composite Materials (Amer. Soc. for Metals, Ohio, 1965).
B. Budiansky and N. A. Fleck, “Compressive Failure of Fiber Composites,” J. Mech. Phys. Solids. 41 (1), 183–211 (1993).
K. H. Lo and E. S. M. Chim, “Compressive Strength of Unidirectional Composites,” J. Reinforced Plast. Compos. 11 (8), 838–896 (1992).
Y. L. Xu and K. L. Reifsnider, “Micromechanical Modeling of Composite Compressive Strength,” J. Compos. Mater. 27 (6), 572–588 (1993).
A. Jumahat, C. Soutis, F. R. Jones, and A. Hodzic, “Fracture Mechanisms and Failure Analysis of Carbon Fibre/Toughened Epoxy Composites Subjected to Compressive Loading,” Compos. Struct. 92 (2), 295–305 (2010).
M. Meng, H. R. Le, M. J. Rizvi, and S. M. Grove, “The Effects of Unequal Compressive/Tensile Moduli of Composites,” Compos. Struct. 126, 207–215 (2015).
J. Ye, Y. Qiu, X. Chen, and J. Ma, “Initial and Final Failure Strength Analysis of Composites Based on a Micromechanical Method,” Compos. Struct. 125, 328–335 (2015).
T. J. Vaughan and C. T. McCarthy, “A Combined Experimental-Numerical Approach for Generating Statistically Equivalent Fibre Distributions for High Strength Laminated Composite Materials,” Compos. Sci. Technol. 70 (2), 291–297 (2010).
Ramesh Talreja, “Assessment of the Fundamentals of Failure Theories for Composite Materials,” Composite Sci. Technol. 105, 190–201 (2014).
M. Hojo, M. Mizuno, T. Hobbiebrunken, et al., “Effect of Fiber Array Irregularities on Microscopic Interfacial Normal Stress States of Transversely Loaded UD-CFRP from Viewpoint of Failure Initiation,” Compos. Sci. Technol. 69 (11/12), 1726–1734 (2009).
V. N. Paimushin, N. V. Polyakova, S. A. Kholmogorov, and M. A. Shishov, “Non-Uniformly Scaled Buckling Modes of Reinforcing Elements in Fiber Reinforced Plastic,” Izv. Vyssh. Uchebn. Zaved., Mat. 61 (9), 89–95 (2017) [Russ. Math. 61 (9), 79–84 (2017)].
V. N. Paimushin and V. I. Shalashilin, “Relations of the Theory of Deformations in the Quadratic Approximation and the Problem of Constructing Refined Versions of the Geometrically Nonlinear Theory of Layered Structural Elements,” Prikl. Mat. Mekh. 69 (5), 861–881 (2005).
V. N. Paimushin, “Problems of Geometric Nonlinearity and Stability in the Mechanics of Thin Shells and Rods with a Rectilinear Axis,” Prikl. Mat. Mekh. 71 (5), 855–893 (2007).
V. N. Paimushin and N. V. Polyakova, “Consistent Equations of the Theory of Flat Curvilinear Rods with Finite Displacements and Linearized Problems of Stability,” Prikl. Mat. Mekh. 73 (2), 303–324 (2009).
Author information
Authors and Affiliations
Corresponding author
Additional information
Original Russian Text © V.N. Paimushin, R.K. Gazizullin, M.A. Shishov.
Translated from Prikladnaya Mekhanika i Tekhnicheskaya Fizika, Vol. 60, No. 3, pp. 173–185, May–June, 2019.
Rights and permissions
About this article
Cite this article
Paimushin, V.N., Gazizullin, R.K. & Shishov, M.A. Flat Internal Buckling Modes of Fibrous Composite Elements under Tension and Compression at the Mini- and Microscale. J Appl Mech Tech Phy 60, 548–559 (2019). https://doi.org/10.1134/S0021894419030180
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1134/S0021894419030180