Possible Search for Majorana Neutrinos at Future Lepton Colliders

We discuss the process ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{W}^{ \pm }}{{\ell }^{ \mp }}$, where N is a heavy Majorana neutrino and $\ell = e,\mu$. Large cross sections are expected for these processes at high center-of-mass energies, which can be reached at future lepton–lepton colliders. The Monte Carlo simulation of the studied processes is produced within the framework of the seesaw type-I model, where the Majorana neutrinos (or heavy neutral leptons, HNL), are introduced in the standard leptonic sector. Recently the possibility to search for the direct HNL production was studied in the ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{\nu }_{\ell }}$ process with the subsequent decay $N \to {{W}^{ \pm }}{{\ell }^{ \mp }}$. In this paper we investigate an alternative process ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{W}^{ \pm }}{{\ell }^{ \mp }} \to {{W}^{ \pm }}{{W}^{ \pm }}{\kern 1pt} {{\ell }^{ \mp }}{\kern 1pt} {{\ell }^{ \mp }}$ with the lepton number violation by two units. The similar processes appear in collisions with the same-sign beams, ${{e}^{ - }}{{e}^{ - }} \to N{{W}^{ - }}{\kern 1pt} {{e}^{ - }} \to {{W}^{ - }}{\kern 1pt} {{W}^{ - }}{\kern 1pt} {{e}^{ + }}{\kern 1pt} {{e}^{ - }}$ or ${{\mu }^{ + }}{{\mu }^{ + }}$ $\to$ $N{{W}^{ + }}{\kern 1pt} {{\mu }^{ + }} \to {{W}^{ + }}{\kern 1pt} {{W}^{ + }}{\kern 1pt} {{\mu }^{ + }}{\kern 1pt} {{\mu }^{ - }}$. The cross sections of the processes under consideration are enhanced by the soft photon exchange in the t-channel. We calculate the cross sections for the signals and potential Standard Model backgrounds for the ${{e}^{ + }}{{e}^{ - }}$ beam collisions at the 1 TeV center-of-mass energy and the ${{\mu }^{ + }}{{\mu }^{ - }}$ collisions at 3 and 10 TeV. Due to the diagrams with soft t-channel photons and respective interference the promptly emitted leptons are produced in the direction close to the corresponding beam. These leptons will be lost in the beam pipe or badly measured by forward detectors. However, the signal events can be well separated from backgrounds using the rest of the event containing the $WW\ell$ particles. Finally, the expected upper limits on the mixing parameters ${{\left| {{{V}_{{\ell N}}}} \right|}^{2}}$ as a function of M(N) are calculated.

1. INTRODUCTION

Neutrinos of the Standard Model (SM) can be Majorana fermions, origin of their masses is associated with a violation of $U{{(1)}_{{B - L}}}$ global invariance of the SM Lagrangian. As a result, very rare interaction processes with a violation of the lepton number (LNV processes) may be possible. Very small masses of the standard (or active) neutrinos are explained within the framework of extensions of the SM leptonic sector by introducing of Majorana neutrinos (or heavy neutral leptons, HNL). In the processes involving HNL the violation of lepton number can be experimentally observed.

The current experimental upper limits on the HNL mixing parameters ${\text{|}}{{V}_{{lN}}}{\text{|}},l = e,\mu ,\tau$ as a function of the HNL mass are summarized in [1]. The mass interval from 0.1 GeV to a few GeV is covered by the extracted beam experiments with missing energy reconstruction and the experiments with displaced vertices. The mass interval up to TeV scale is a range for collider experiments. Rather strict upper limits have been obtained at LEP for the HNL masses up to the Z boson mass [2], however, the limits on the HNL masses higher than 100 GeV were rather weak. A strong limit for the squared sum ${\text{|}}\sum\nolimits_i V_{{e{{N}_{i}}}}^{2}{\text{/}}M({{N}_{i}}){\text{|}} \leqslant 1.8 \times {{10}^{{ - 8}}}$ GeV^–1 has been obtained within the seesaw type-I scenario from the neutrinoless double beta ($0\nu \beta \beta$) decays [3]. However, this limit can be circumvented in case of the three generations of the heavy HNL and a specific combination of $CP$ phases in the PMNS matrix [4]. Updated experimental upper limits on the mixing parameters for the HNL masses larger than 100 GeV have been provided by the LHC run II data [5–7], better limits are expected with the future LHC luminosity upgrade [2, 8–10]. A significant improvement of these upper limits can be reached at future high energy lepton colliders [11].

Simulation of the HNL production in collider experiments demonstrated realistic possibilities of the signal searches in the ${{e}^{ + }}{{e}^{ - }}$, ${{e}^{ - }}{{e}^{ - }}$, ${{\mu }^{ + }}{{\mu }^{ - }}$, and ${{\mu }^{ + }}{{\mu }^{ + }}$ beam colliders at TeV energies. After the partonic level calculation of the process ${{e}^{ + }}{{e}^{ - }} \to q\bar {q}e\nu$ at LEP2 [12] performed for complete set of 2 → 4 diagrams by means of CompHEP [13, 14], a number of detailed studies for the signal separation from the SM backgrounds including detector simulation has been performed. In [11] a study for the channel ${{e}^{ + }}{{e}^{ - }} \to N\nu \to q\bar {q}l\nu$ at ILC and CLIC energies by the chain of the FeynRules [15], Whizard [16], and Delphes [17] packages is presented. A field-theoretic model is defined in the FeynRules package, event generation is done by Whizard. Detector simulation and event reconstruction is performed by Delphes, thereby providing a realistic simulation of all final state objects. Potential to search for HNL in the ${{\mu }^{ + }}{{\mu }^{ - }} \to N\nu \to q\bar {q}l\nu$ process at TeV energies has been studied in [18] and [19] using the FeynRules, Whizard, and Delphes chain and in [20] using the FeynRules, Madgraph5 [21], and Delphes chain. In these studies of the ${{\ell }^{ + }}{{\ell }^{ - }} \to N\nu \to q\bar {q}\ell \nu$ processes the upper limits for the mixing parameter are obtained to be ${\text{|}}{{V}_{{\ell N}}}{{{\text{|}}}^{2}} \sim {{10}^{{ - 5}}}{-}{{10}^{{ - 7}}}$ at integrated luminosities of about a few ab^–1 and the collision CM energy in the range of 1–10 TeV. Although background contributions under the signals are large, a good signal separation was achieved by using a set of discriminating variables calculated in the final state. The HNL production via the vector boson scattering process at high energy muon colliders was studied in [22]. An opportunity to search for HNL at ${{e}^{ - }}p$ collisions with TeV protons and 60-GeV electrons has been discussed at [23].

The production of the heavy Majorana neutrinos in the ${{e}^{ + }}{{e}^{ - }}{\kern 1pt} \to {\kern 1pt} N{{W}^{ + }}{{e}^{ - }}$ and ${{\mu }^{ + }}{{\mu }^{ - }}{\kern 1pt} \to {\kern 1pt} N{{W}^{ + }}{{\mu }^{ - }}$ processes is studied in this paper using the chain of the LanHEP [24], CompHEP, Pythia6 [25], and Delphes packages. A field-theoretic model is defined in LanHEP package, event generation is done by CompHEP, the decays of HNL and W bosons and hadronization are executed by Pythia, and detector simulation is performed by Delphes. The produced Majorana neutrinos decay in the $N \to {{W}^{ + }}{{e}^{ - }}$ and $N \to {{W}^{ + }}{{\mu }^{ - }}$ modes resulting in the lepton number violation by two units. These processes are permitted only in case of the Majorana neutrinos and have a clear experimental signature. The charge-conjugated processes are assumed by default everywhere in the paper. Similar processes ${{e}^{ - }}{{e}^{ - }} \to N{{W}^{ - }}{{e}^{ - }}$ and ${{\mu }^{ + }}{{\mu }^{ + }} \to N{{W}^{ + }}{{\mu }^{ + }}$ are possible in the same-sign beam collisions.

The ${{e}^{ + }}{{e}^{ - }} \to N{{W}^{ + }}{{e}^{ - }}$ process was studied in [26] at the CM energies 350 and 500 GeV using the chain of the FeynRules and Madgraph5 packages. However, all final state particles were required to be reconstructed in this study, that resulted in a very small number of the expected signal events.

It has to be noted, that the direct production of HNL at lepton–lepton collisions provides a high sensitivity to the mixing parameter ${\text{|}}{{V}_{{\ell N}}}{{{\text{|}}}^{2}}$, because the process contains only one $NW\ell$ vertex. The process ${{\mu }^{ + }}{{\mu }^{ + }} \to {{W}^{ + }}{{W}^{ + }}$ with two such vertices gives worser upper limits, but its sensitivity to the HNL masses is higher than the CM energy [4, 27, 28].

2. SEESAW TYPE-I MODEL

Neutrino mass generation using a seesaw type-I mechanism is performed by means of a Lagrangian [29]

$$\begin{gathered} \mathcal{L} = {{\mathcal{L}}_{{SM}}} + i{{{\bar {\nu }}}_{R}}{{\gamma }^{\mu }}{{\partial }_{\mu }}{{\nu }_{R}} \\ - \left( {F{{{\overline L }}_{l}}\tilde {H}{{\nu }_{R}} + \frac{1}{2}{{M}_{M}}\bar {\nu }_{R}^{c}{{\nu }_{R}} + {\text{H}}{\text{.c}}} \right), \\ \end{gathered} $$

(1)

where ${{L}_{l}} = ({{\nu }_{l}},{\kern 1pt} l)_{L}^{T}$ is the left lepton doublet, ${{\nu }_{R}}$ are HNL flavor states, ${{({{\nu }_{R}})}^{c}} \equiv C\bar {\nu }_{R}^{T}$ ($C = i{{\gamma }_{2}}{{\gamma }_{0}}$), $H$ is the Higgs doublet ($\tilde {H} = i{{\tau }_{2}}H{\text{*}}$, τ₂ is the Pauli matrix), F is the Yukawa matrix 3 × 3 and M_M is the Majorana mass matrix, $M_{M}^{T} = {{M}_{M}}$. After spontaneous symmetry breaking the Yukawa matrix ${{M}_{D}} = F{v}{\text{/}}\sqrt 2$ (${v} =$ 246 GeV) and the Majorana mass matrix M_M form a complete 6 × 6 mass matrix in the extended lepton sector

$$\begin{gathered} \frac{1}{2}({{{\bar {\nu }}}_{L}}\bar {\nu }_{R}^{c})\mathcal{M}\left( {\begin{array}{*{20}{c}} {\nu _{L}^{c}} \\ {{{\nu }_{R}}} \end{array}} \right) + {\text{H}}{\text{.c}}{\text{.}} \\ = \frac{1}{2}({{{\bar {\nu }}}_{L}}\bar {\nu }_{R}^{c})\left( {\begin{array}{*{20}{c}} 0&{{{M}_{D}}} \\ {M_{D}^{T}}&{{{M}_{M}}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\nu _{L}^{c}} \\ {{{\nu }_{R}}} \end{array}} \right) + {\text{H}}{\text{.c}}., \\ \end{gathered} $$

(2)

where the flavor states ${{({{\nu }_{L}})}_{\alpha }},({{\nu }_{R}}{{)}_{I}}$ and the mass states ${{\nu }_{k}},{{N}_{I}}$ ($\alpha = e,\mu ,\tau$, $k,I = 1,2,3$) are connected by the transformation

$$\left( {\begin{array}{*{20}{c}} {{{\nu }_{L}}} \\ {\nu _{R}^{c}} \end{array}} \right) = \mathcal{U}{{P}_{L}}\left( {\begin{array}{*{20}{c}} \nu \\ N \end{array}} \right), \quad \mathcal{U} = \mathcal{W}{\text{diag}}({{U}_{\nu }},U_{N}^{*}).$$

(3)

${{P}_{L}} = (1 - {{\gamma }_{5}}){\text{/}}2$, and ${{U}_{\nu }},{{U}_{N}}$ are unitary 3 × 3 matrices. Block-diagonal form of the mass matrix (2) looks as

$$\begin{gathered} {{\mathcal{U}}^{\dag }}\mathcal{M}\mathcal{U}{\text{*}} = \left( {\begin{array}{*{20}{c}} {U_{\nu }^{\dag }}&0 \\ 0&{U_{N}^{T}} \end{array}} \right){{\mathcal{W}}^{\dag }}\mathcal{M}\mathcal{W}{\text{*}}\left( {\begin{array}{*{20}{c}} {U_{\nu }^{*}}&0 \\ 0&{{{U}_{N}}} \end{array}} \right) \\ = \left( {\begin{array}{*{20}{c}} {U_{\nu }^{\dag }{{m}_{\nu }}U_{\nu }^{*}}&0 \\ 0&{U_{N}^{T}{{M}_{N}}{{U}_{N}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\hat {m}}&0 \\ 0&{\hat {M}} \end{array}} \right), \\ \end{gathered} $$

(4)

where $\hat {m}$ and $\hat {M}$ are diagonal mass matrices for active neutrinos and HNL, ${{\mathcal{W}}^{\dag }}\mathcal{M}\mathcal{W} = {\text{diag}}({{m}_{\nu }},\;{{M}_{N}})$, $\mathcal{M}$ is defined by Eq. (2). In the following diagonalization procedure [30, 31] the unitary $\mathcal{W}$-matrix is represented as an exponent of a skew-Hermitian matrix

$$\mathcal{W} = \exp \left( {\begin{array}{*{20}{c}} 0&\theta \\ { - {{\theta }^{\dag }}}&0 \end{array}} \right),$$

(5)

and decomposed to second-order terms by θ. As a result, we obtain a connection of mass states and flavor states in the form

$$\begin{gathered} {{\nu }_{L}} \simeq \left( {1 - \frac{1}{2}\theta {{\theta }^{\dag }}} \right){{U}_{\nu }}{{P}_{L}}\nu + \theta U_{N}^{*}{{P}_{L}}N, \\ \nu _{R}^{c} \simeq - {{\theta }^{\dag }}{{U}_{\nu }}{{P}_{L}}\nu + \left( {1 - \frac{1}{2}{{\theta }^{\dag }}\theta } \right)U_{N}^{*}{{P}_{L}}N. \\ \end{gathered} $$

(6)

The first term in (6) corresponds to the well-known phenomenological relation which defines the PMNS mixing matrix ${{\nu }_{{L\alpha }}} = \sum\nolimits_\alpha {{({{U}_{{{\text{PMNS}}}}})}_{{\alpha j}}}{{P}_{L}}{{\nu }_{j}}$ [32, 33]. Deviation from unitarity for the PMNS matrix is defined by the term $- \frac{1}{2}\theta {{\theta }^{\dag }}$. The Lagrangian terms for neutrino mass states and HNL mass states interaction with ${{W}^{ \pm }},Z$ bosons have the form

$$\begin{gathered} \mathcal{L}_{{NC}}^{\nu } = - \frac{g}{{2{{c}_{W}}}}{{\gamma }^{\mu }}{{{\bar {\nu }}}_{L}}U_{{{\text{PMNS}}}}^{{{\dag }}}{{U}_{{{\text{PMNS}}}}}{{\nu }_{L}}{{Z}_{\mu }}, \\ \mathcal{L}_{{CC}}^{\nu } = - \frac{g}{{\sqrt 2 }}{{\overline l }_{L}}{{\gamma }^{\mu }}{{U}_{{{\text{PMNS}}}}}{{\nu }_{L}}W_{\mu }^{ - } + {\text{H}}{\text{.c}}., \\ \mathcal{L}_{{NC}}^{N} = - \frac{g}{{2{{c}_{W}}}}{{{\bar {N}}}_{L}}{{\gamma }^{\mu }}U_{N}^{T}{{\theta }^{\dag }}\theta U_{N}^{*}{{N}_{L}}{{Z}_{\mu }} \\ - \left[ {\frac{g}{{2{{c}_{W}}}}{{{\bar {\nu }}}_{L}}{{\gamma }^{\mu }}U_{\nu }^{\dag }\theta U_{N}^{*}{{N}_{L}}{{Z}_{\mu }} + {\text{H}}{\text{.c}}{\text{.}}} \right], \\ \mathcal{L}_{{CC}}^{N} = - \frac{g}{{\sqrt 2 }}{{\overline l }_{L}}{{\gamma }^{\mu }}\theta U_{N}^{*}{{N}_{L}}W_{\mu }^{ - } + {\text{H}}{\text{.c}}., \\ \end{gathered} $$

(7)

HNL mixing is defined in the approximation $\mathcal{W} \sim$ $\mathcal{O}({{\theta }^{2}})$ as $\Theta \equiv \theta U_{N}^{*}$. The active neutrino mass matrix is defined in the framework of $\mathcal{O}({{\theta }^{2}})$ scenario by the seesaw type I equation

$${{m}_{\nu }} \simeq - {{M}_{D}}{{\theta }^{T}} \simeq - {{M}_{D}}M_{M}^{{ - 1}}M_{D}^{T},$$

(8)

with ambiguous definition of M_D by means of ${{U}_{{{\text{PMNS}}}}}$ and U_N mass matrix of the HNL sector

$${{M}_{D}} = i{{U}_{{{\text{PMNS}}}}}\sqrt {\hat {m}} \Omega \sqrt {\hat {M}} U_{N}^{\dag },$$

(9)

where Ω is an arbitrary orthogonal matrix, $\Omega {{\Omega }^{T}} = I$. Components of the mixing matrix have the form

$${{\Theta }_{{\alpha I}}} = i\frac{{\sum\limits_k \sqrt {{{m}_{k}}} ({{U}_{\nu }}{{)}_{{\alpha k}}}{{\Omega }_{{kI}}}}}{{\sqrt {{{M}_{I}}} }},$$

(10)

where $\alpha = e,\mu ,\tau$ and $I = 1,2,3$ is the number of HNL generation. Mixing for the first generation HNL, which is usually considered as a candidate for the role of a dark matter particle, is determined by the first column of the matrix Ω.

In the simplest “minimal parametric mixing” case of the diagonal $\Omega = I$ matrix the mixing matrix for the normal mass hierarchy (NH) is

$$\Theta _{{\min }}^{{{\text{NH}}}} = \left( {\begin{array}{*{20}{c}} {i{{U}_{{e1}}}\sqrt {\frac{{{{m}_{1}}}}{{{{M}_{1}}}}} }&{i{{U}_{{e2}}}\sqrt {\frac{{{{m}_{2}}}}{{{{M}_{2}}}}} }&{i{{U}_{{e3}}}\sqrt {\frac{{{{m}_{3}}}}{{{{M}_{3}}}}} } \\ {i{{U}_{{\mu 1}}}\sqrt {\frac{{{{m}_{1}}}}{{{{M}_{1}}}}} }&{i{{U}_{{\mu 2}}}\sqrt {\frac{{{{m}_{2}}}}{{{{M}_{2}}}}} }&{i{{U}_{{\mu 3}}}\sqrt {\frac{{{{m}_{3}}}}{{{{M}_{3}}}}} } \\ {i{{U}_{{\tau 1}}}\sqrt {\frac{{{{m}_{1}}}}{{{{M}_{1}}}}} }&{i{{U}_{{\tau 2}}}\sqrt {\frac{{{{m}_{2}}}}{{{{M}_{2}}}}} }&{i{{U}_{{\tau 3}}}\sqrt {\frac{{{{m}_{3}}}}{{{{M}_{3}}}}} } \end{array}} \right).$$

For inverted hierarchy (IH) the antidiagonal Ω is used. One can observe using the HNL currents of Eq. (7) that the HNL production cross sections in the lowest order include the factor ${\text{|}}\Theta {{{\text{|}}}^{{\text{2}}}}$, so they are strongly suppressed by m/M mass ratio. In the recent literature, more interesting choice is considered on an almost non-alternative basis

$$\begin{gathered} \;\;{\kern 1pt} {{\Omega }^{{{\text{NH}}}}} = \left( {\begin{array}{*{20}{c}} 1&0&0 \\ 0&{\cos (\omega )}&{ - \sin (\omega )} \\ 0&{\xi \sin (\omega )}&{\xi \cos (\omega )} \end{array}} \right), \\ {\text{or}} {{\Omega }^{{{\text{IH}}}}} = \left( {\begin{array}{*{20}{c}} 0&{\cos (\omega )}&{ - \sin (\omega )} \\ 0&{\xi \sin (\omega )}&{\xi \cos (\omega )} \\ 1&0&0 \end{array}} \right). \\ \end{gathered} $$

(11)

Production enhancements appear with the complex-valued $\omega$ parameter which leads to the factors ${{X}_{\omega }}{\kern 1pt}$ = exp$({\text{Im}}(\omega ))$ in the mixing matrix $\Theta$. An analysis of active and sterile neutrino mixing in [34] demonstrated that a phenomenologically consistent hierarchy of mixings ${{\Theta }_{{eI}}}$, ${{\Theta }_{{\mu I}}}$, and ${{\Theta }_{{\tau I}}}$ with ${{\Theta }_{{eI}}}$ suppression relative to other mixing matrix elements can be achieved in a wide interval of ${{X}_{\omega }}$ independently on the values of HNL masses. The experimental upper bounds on ${{\Theta }_{{\alpha I}}}$ from the shortest possible lifetimes of ${{N}_{{2,3}}}$ from π^± and K^± meson decays converted into the upper bound on ${{X}_{\omega }}$ lead to Im$(\omega ) = 4.5$ at the HNL mass of the order of 10² MeV for the lifetime of the order of 1 sec and Im$(\omega ) \sim 7$ for the lifetime of the order of 0.01 s. Values of the $\omega$ parameter greater than seven can lead to a large mixing parameters not consistent with the EW data of high precision. Recent reconsideration in the light of modern data for HNL searches in the mass range less than the mass of K meson has been performed in [35] for the case of two HNL generations. Model-dependence of $\Theta$-mixing results in a rather non-trivial set of consequences for the observables. For this reason collider studies are performed in the framework of the so-called “model-independent phenomenological approach” [36] or, in other words, “phenomenological type I seesaw model” [37]. In the model-independent phenomenological approach it is assumed that only a single HNL is available in an experiment, while other HNLs are sufficiently heavy and do not affect the analysis. There are only two independent parameters in this approach, the HNL mass and the Yukawa coupling defining HNL interaction with an active neutrino of a given flavor, assuming that the mixing with other flavors is zero. In the phenomenological type I seesaw model an additional parameter distinguishing Dirac neutrino case from Majorana neutrino case is added, which allows to discriminate observables specific for the field-theoretic model. Such simplifications are useful for derivation of generic bounds on the mixing parameter beyond any aspects of a particular model construction, but need an appropriate translation if one would like to go beyond the case of one generation and consider a well-defined mixing.

In the following analysis based on Casas–Ibarra diagonalization the mixing factor including $\sqrt {m{\text{/}}M}$ is enhanced by taking Im$(\omega ) = 3$, then evaluating ${{\Theta }_{{\alpha I}}}$. This approach is different from the specific mixing scenarios in the pseudo-Dirac limit, where an additional flavor symmetry is used to reconcile very small active neutrino masses with large mixings to give observable signals with HNL at the electroweak scale. Explicit expressions for the ${{\Theta }_{{\alpha I}}}$ as a function of Im$(\omega )$ are given in [34].

3. EXPERIMENTAL PROCEDURE

A. Monte Carlo Simulation and Reconstruction

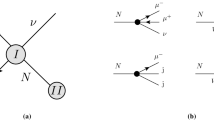
The signal processes ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{W}^{ \pm }}{{\ell }^{ \mp }}$ with $\ell = e,\mu$ are modelled using the CompHEP generator [13], where the seesaw type-I model is incorporated. As mentioned above, for simplicity only one Majorana neutrino is included in the calculations, which is labeled as N everywhere in the following text. Other two HNLs decouple. The calculations include the matrix elements for all possible diagrams at the parton level, which are allowed for the studied process. The 30 diagrams are obtained in the CompHEP generator to describe the signal process. Two of these diagrams with t-channel vector bosons are shown in Fig. 1.

Fig. 1.

(Color online) Two examples of diagrams describing the process ${{e}^{ + }}{{e}^{ - }} \to N{{W}^{ + }}{\kern 1pt} {{e}^{ - }}$.

The CompHEP generator evaluates the cross sections for the studied processes and produces the Monte Carlo (MC) event data samples. We generated the process ${{e}^{ + }}{{e}^{ - }} \to N{{W}^{ + }}{{e}^{ - }}$ at the CM energy 1 TeV and the process ${{\mu }^{ + }}{{\mu }^{ - }} \to N{{W}^{ + }}{{\mu }^{ - }}$ at the CM energy 3  and 10 TeV. The beams are assumed to be unpolarized. The HNL mass is varied in the range from 100 GeV to the CM energy. The HNL width is assumed to increase with the HNL mass similar to that obtained in [11]. The HNL width variation within 20% results in cross section variation of less than 1%.

The subsequent decays $N \to {{W}^{ \pm }}{{\ell }^{ \mp }}$ and ${{W}^{ \pm }} \to q\bar {q}$ are modelled by Pythia6. Only hadronic decays of the W bosons are used. We forced the decay angle $\theta _{\ell }^{ \star }$ of the lepton in the HNL rest frame relative to the HNL direction to follow the $f(\theta _{\ell }^{ \star }) = (1 - \cos (\theta _{\ell }^{ \star }$))/2 distribution. The ISR effects are included on the level of Pythia6. Finally, the quarks are hadronized by Pythia6. The SM background data samples are produced by the Whizard 2 generator which contains Pythia6. The same beams and CM energies as for the signal samples are used to generate backgrounds. The produced signal and background data samples are processed with the Delphes program [17], which provides the fast and simplified detector simulation and the event reconstruction. In Delphes the ILC detector card is used in case of the ${{e}^{ + }}{{e}^{ - }} \to N{{W}^{ + }}{{e}^{ - }}$ process at 1 TeV, and the MuC detector card is used for the ${{\mu }^{ + }}{{\mu }^{ - }} \to N{{W}^{ + }}{{\mu }^{ - }}$ process at 3 and 10 TeV. The jets are reconstructed using the Valencia algorithm with the default parameters. The Delphes jet algorithm is forced to reconstruct exactly four jets. The produced output data samples comprise the information about the four-momenta of the reconstructed jets and the isolated leptons. The signal and background data samples produced by Delphes are analyzed using the ROOT package.

B. Cross Sections

The cross sections for the ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{W}^{ + }}{{\ell }^{ - }}$ processes calculated by the CompHEP program are shown in Fig. 2. The mixing parameter is fixed to ${\text{|}}{{V}_{{\ell N}}}{{{\text{|}}}^{2}}$ = 0.0003 to compare our results with [11], where this value was used. The cross sections for the ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{\nu }_{\ell }}$ processes computed by CompHEP are also shown in Fig. 2. The same beams, CM energies, and mixing parameters are assumed for both processes. Unitary cancellation of the second order t-channel pole, see Fig. 1 (right diagram) is checked directly using $d\sigma {\text{/}}d({\text{ln}}t)$ distribution [38]. The ${{\ell }^{ + }}{{\ell }^{ - }}\, \to \,N{{\nu }_{\ell }}$ process cross sections obtained with CompHEP agree perfectly with the cross sections calculated in [11] using the Whizard 2 generator.

Fig. 2.

(Color online) Cross sections for (purple line) the process ${{e}^{ + }}{{e}^{ - }} \to N{{W}^{ + }}{{e}^{ - }}$ at 1 TeV and (red and blue lines) the process ${{\mu }^{ + }}{{\mu }^{ - }} \to N{{W}^{ + }}{{\mu }^{ - }}$ at 3 and 10 TeV, respectively, versus the HNL mass in comparison with (dashed brown lines) the cross sections for the processes ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{\nu }_{\ell }}$ for the same mixing parameter, beam particles, and CM energies. The factor 2 reflects two charge-conjugated final states.

As we can see in Fig. 2, the plateau in the cross section of the ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{W}^{ \pm }}{{\ell }^{ \mp }}$ process is growing with the CM energy in contrast to the ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{\nu }_{\ell }}$ process. At high CM energies the process ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{W}^{ \pm }}{{\ell }^{ \mp }}$ has large cross sections and can be used to obtain strong upper limits on the mixing parameters. Additional advantages of this process are a high signal reconstruction efficiency and a high signal to background separation ratio.

C. Selections

The process ${{\ell }^{ + }}{{\ell }^{ - }} \to {{W}^{ + }}{\kern 1pt} {{W}^{ + }}{{\ell }^{ - }}{{\ell }^{ - }}$ includes two same-sign leptons and four jets in the final state. Although there is no SM background to this final state, the reconstruction efficiency is below a percent level. One of the final state leptons is mostly emitted close to the beam direction and is not registered in detectors or badly measured in forward calorimeters. Therefore, we will not discuss the signature with all particles reconstructed.

We select the final states with four jets and one lepton. The initial preselections are applied on the energy and pseudorapidity of the jets and the lepton:

$$E(j) > 10 {\text{ GeV}};\quad E(\ell ) > 10 {\text{ GeV}};$$

$${\text{|}}\eta (j){\text{|}} < 2.5;\quad {\text{|}}\eta (\ell ){\text{|}} < 2.5.$$

(12)

The jets are produced in the W boson decays, respectively we combine the four jets in the two bosons. Among possible combinations, the two jet pairs with the invariant masses closest to the nominal W boson mass are chosen as the W candidates. If a W boson has a large energy, the produced jets can be partially overlapped. In this case the parameters of the individual jets can be incorrect, however the respective two-jet combination reproduces the W boson mass and momentum with a reasonable accuracy.

To separate signal events from backgrounds we use the following variables:

(i) the missing mass ${{M}_{{{\text{miss}}}}}(4j{\kern 1pt} {{\ell }^{ - }})$ to the sum of the four jets and the reconstructed lepton,

(ii) the masses $M(jj)$ of jet pairs corresponding to the $W$ boson candidates,

(iii) the cosine cos$({{W}_{1}} \vee {{W}_{2}})$ of the angle between two $W$ candidates,

(iv) the cosine cos$({{\ell }^{ - }} \vee \ell _{{{\text{beam}}}}^{ - })$ of the angle between the directions of the reconstructed lepton and the same-sign beam lepton,

(v) the cosine cos(${{P}_{{{\text{miss}}}}}(4j{\kern 1pt} {{\ell }^{ - }}) \vee \ell _{{{\text{beam}}}}^{ - }$) of the angle between the missing momentum (to the four-jet and the isolated lepton) and the same-sign beam lepton,

(vi) the invariant masses ${{M}_{\Delta }}(W{{\ell }^{ - }})$ of the W boson and the reconstructed lepton (two combinations).

The cut on the variable ${{M}_{{{\text{miss}}}}}(4j{\kern 1pt} {{\ell }^{ - }})$ is used to remove the backgrounds with two or more unobserved particles, because such backgrounds must have a large missing mass. The mass of the jet pairs is required to lie in the range $50 < M(jj) < 120{\kern 1pt}$ GeV for the selected $W$ candidates. The backgrounds with only one produced W or Z boson decaying in two jets can imitate four-jet configuration. This background must have a small angle between the W candidates, and the cut cos$({{W}_{1}} \vee {{W}_{2}}) < 0.8$ is applied to suppress this background. The backgrounds coming from the vector boson fusion processes should result in a small lepton angle relative to the corresponding beam direction. The cut cos$({{\ell }^{ - }} \vee \ell _{{{\text{beam}}}}^{ - }) < 0.7$ is used to provide a significant suppression of these backgrounds. This cut also suppresses the backgrounds, where a lepton is produced in the decay of the $W$ boson. As it was explained above, the unobserved lepton is mostly emitted with a small angle relative to the direction of the corresponding beam. The sign of the beam is fixed by the sign of the reconstructed lepton. Therefore, the momentum of the system of the four jets and lepton can be used to estimate the direction of the missed lepton. The variable cos(${{P}_{{{\text{miss}}}}} \vee \ell _{{{\text{beam}}}}^{ - }$) is peaked at 1 for the signal events, except the events with the NHL mass close to ${{E}_{{{\text{cms}}}}}$. In contrast, the backgrounds due to vector boson fusion production peak at –1, whereas other backgrounds have flat distributions. Therefore, the cut cos(${{P}_{{{\text{miss}}}}} \vee \ell _{{{\text{beam}}}}^{ - }) > 0.9$ is applied for all HNL mass values, except the high HNL mass region, where this signal distribution becomes flat. The applied cuts are summarized in Table 1. Finally, the distributions of the invariant mass of the W boson and the reconstructed lepton ${{M}_{\Delta }}(W{{\ell }^{ - }}$) have to be searched for a peak corresponding to the HNL production. The mass difference ${{M}_{\Delta }}(W{{\ell }^{ - }}) = M(jj{{\ell }^{ - }}) - M(jj$) + 80.377 is used instead of $M(jj{{\ell }^{ - }}$) to improve the signal resolution especially at the low HNL mass region up to 500 GeV.

Table 1. Cuts on the variables applied at different CM energies. The last column shows the cuts applied at the high HNL mass region $M(N) > 0.85{{E}_{{{\text{cms}}}}}$, where the cut on cos(${{P}_{{{\text{miss}}}}} \vee \ell _{{{\text{beam}}}}^{ - }$) is removed

D. Backgrounds

For simplicity, the electron beam channel is considered in this section, however almost the same analysis is performed for the muon beam channels. The studied backgrounds are required to have one identified isolated lepton. The isolated leptons can be produced in the W or Z boson decays or in the vector boson fusion processes. Backgrounds with a faked lepton are not studied here, these backgrounds are expected to give a small contribution. The four jets are required to be reconstructed, however there are backgrounds where the two jets are split and imitate the four jets.

We assumed an integrated luminosity of 1 ab^–1 for both ${{e}^{ + }}{{e}^{ - }}$ collisions at 1 TeV and ${{\mu }^{ + }}{{\mu }^{ - }}$ collisions at 3 TeV. An integrated luminosity of 10 ab^–1 is assumed for the ${{\mu }^{ + }}{{\mu }^{ - }}$ collisions at 10 TeV. The cross sections for all potentially dangerous backgrounds are evaluated using the Whizard 2 generator, and the approximate numbers of events expected to contribute in the ${{M}_{\Delta }}(W{{\ell }^{ - }})$ distribution are calculated. If the estimated numbers of events are not too small, the event data samples are generated to obtain a more accurate estimates. The pseudorapidity cut ${\text{|}}\eta ({{\ell }^{ - }}){\text{|}} < 2.6$ is applied on the level of the background generation for the negative leptons directly produced in the vector boson fusion processes. The six background channels are generated, which are supposed to be potentially dangerous:

(i) ${{e}^{ + }}{{e}^{ - }} \to {{W}^{ + }}(q\bar {q}){\kern 1pt} {{e}^{ - }}{{\nu }_{e}}$,

(ii) ${{e}^{ + }}{{e}^{ - }} \to {{W}^{ + }}(q\bar {q}){{W}^{ - }}({{e}^{ - }}{{\nu }_{e}})$,

(iii) ${{e}^{ + }}{{e}^{ - }} \to {{W}^{ + }}(q\bar {q})Z(q\bar {q}){\kern 1pt} {{e}^{ - }}{{\nu }_{e}}$,

(iv) ${{e}^{ + }}{{e}^{ - }} \to {{W}^{ + }}(q\bar {q}){{W}^{ - }}(q\bar {q}){\kern 1pt} {{e}^{ + }}{{e}^{ - }}$,

(v) ${{e}^{ + }}{{e}^{ - }} \to {{W}^{ + }}(q\bar {q})Z(q\bar {q}){{W}^{ - }}({{e}^{ - }}{{\nu }_{e}})$,

(vi) ${{\gamma }^{B}}{{e}^{ - }} \to {{W}^{ + }}(q\bar {q}){{W}^{ - }}(q\bar {q}){\kern 1pt} {{e}^{ - }}$.

Here the photons produced from bremsstrahlung process are assigned as ${{\gamma }^{B}}$. Figure 3 demonstrates the distributions of the introduced above variables for specific backgrounds at 3 TeV ${{\mu }^{ + }}{{\mu }^{ - }}$ collisions. The corresponding distributions at 1 and 10 TeV have very similar shapes.

Fig. 3.

(Color online) Distributions for the (a) ${{M}_{{{\text{miss}}}}}(4j{{\ell }^{ - }})$, (b) $M(jj)$, (c) cos$({{W}_{1}} \vee {{W}_{2}})$, (d) cos$({{\ell }^{ - }} \vee \ell _{{{\text{beam}}}}^{ - })$, (e) $\cos ({{P}_{{{\text{miss}}}}}(4j{{\ell }^{ - }}) \vee \ell _{{{\text{beam}}}}^{ - }$), and (f) ${{M}_{\Delta }}(W{{\ell }^{ - }})$ parameters for the ${{\mu }^{ + }}{{\mu }^{ - }}$ collisions at a CM energy of 3 TeV. The black histograms are obtained for the signal process ${{\mu }^{ + }}{{\mu }^{ - }} \to N{{W}^{ + }}{{\mu }^{ - }}$ with $M(N) = 600$ GeV. The signal in figure (b) is multiplied by factor 4. The color histograms show the background distributions for the processes (blue) ${{\mu }^{ + }}{{\mu }^{ - }} \to {{W}^{ + }}(q\bar {q})Z(q\bar {q}){\kern 1pt} {{\mu }^{ - }}{{\nu }_{\mu }}$, (red) μ⁺μ^– → ${{W}^{ + }}(q\bar {q})Z(q\bar {q}){{W}^{ - }}({{\mu }^{ - }}{{\nu }_{\mu }})$, and (purple) μ⁺μ^– → ${{W}^{ + }}(q\bar {q}){{W}^{ - }}({{\mu }^{ - }}{{\nu }_{\mu }})$. The distributions are obtained after preselections, but before main cuts. The background distributions are normalized to the cross sections, the signal distributions are normalized to 1000 events. The green histogram in panel (f) shows the sum of all background distributions at 3 TeV after all cuts.

As we can see from Fig. 3c, the backgrounds with only one $W$ boson are strongly suppressed by the cut cos$({{W}_{1}} \vee {{W}_{2}}) < 0.8$. The backgrounds ${{e}^{ + }}{{e}^{ - }} \to q\bar {q}{\kern 1pt} {{e}^{ - }}{{\nu }_{e}}$ with mass $M(q\bar {q}) > 120{\kern 1pt}$GeV, which are not associated with the W boson, have cross sections of a few fb before cuts, that results in contributions of about 1 event or less. The cross section of the e⁺e^– → $Z(jj)Z(jj){\kern 1pt} {{e}^{ + }}{{e}^{ - }}$ process is about (1–3) fb at the studied CM energies and the contributions from this process are less than 2 events. The backgrounds γ^Bμ^– → ${{W}^{ + }}(q\bar {q}){{W}^{ - }}(q\bar {q}){\kern 1pt} {{\mu }^{ - }}$ give a very small contribution because of the large muon mass and the round beams. The backgrounds due to the $\gamma \gamma$ collisions are suppressed by the ${{M}_{{{\text{miss}}}}}$ cuts. The background from the ${{e}^{ + }}{{e}^{ - }} \to t\bar {t} \to {{W}^{ + }}{{W}^{ - }}b\bar {b}$ process is strongly suppressed by the $M(jj) < 120$ GeV cut.

The production cross sections obtained from Whizard and the numbers of events in the background channels obtained from the generated samples after all cuts are given in Table 2. We obtained the marginal contributions from the backgrounds (i) and (ii) of about a few events after all cuts. Therefore, the background channels with only one vector boson can be neglected. The cross section for the $\gamma {{e}^{ - }} \to {{W}^{ + }}(q\bar {q}){{W}^{ - }}(q\bar {q}){\kern 1pt} {{e}^{ - }}$ background depends on beam parameters and is estimated with a large uncertainty. However, the number of event in this channel is small and this contribution can also be neglected. Although the suppression factors for the background channels (iii)–(iv) are relatively moderate, the cross sections of these backgrounds are not too large. Respectively, the ${{M}_{\Delta }}(W{{\ell }^{ - }})$ distribution with all b-ackgrounds comprised has a relatively small number of events (Fig. 3f). Both combinations of the $W$ boson and the lepton are included in the ${{M}_{\Delta }}(W{{\ell }^{ - }})$ distribution.

Table 2. Cross sections in femtobarn for the studied background channels and the estimated numbers of events after all cuts (in brackets). The cut ${\text{|}}\eta ({{\ell }^{ - }}){\text{|}} < 2.6$ is applied on the generation level for the directly produced negative leptons

E. Upper Limits on Mixing Parameters

The signal events are generated by CompHEP for three CM energies and different HNL masses. Each data sample contains 1000 events, where only $W \to q\bar {q}$ decays are permitted. The reconstructed signals after all cuts are shown in Fig. 4. The CM energies, the HNL masses and the numbers of the signal events in the corresponding mass windows are given in Table 3.

Fig. 4.

(Color online) Signal ${{M}_{\Delta }}(W{{\ell }^{ - }})$ mass distributions for the (a) ${{e}^{ + }}{{e}^{ - }}$ collisions at 1 TeV, (b) ${{\mu }^{ + }}{{\mu }^{ - }}$ collisions at 3 TeV, and (c) ${{\mu }^{ + }}{{\mu }^{ - }}$ collisions at 10 TeV. The signals for the different HNL masses are shown in different colors. Two combinations of the W boson and the lepton are included, except the HNL with the largest mass, where only the combination with the high momentum W is taken. The values of the modelled HNL masses are given in Table 3.

Table 3. Modelled HNL masses, the corresponding production cross sections, and the numbers of signal events in the chosen mass windows are given for the studied CM energies and beams. The data samples of 1000 events are generated for each HNL mass value, only $W \to q\bar {q}$ decays are permitted

To obtain the numbers of signal events the mass windows are chosen respectively to the width of the signals. At the electron beam channels the mass windows are $\pm$10 GeV, except the first and last mass values. At the muon beam channels, the mass window is $[0.94 - 1.03]M(N)$, except the first and last mass values. The windows for the first and last mass values are specially adjusted to observed widths of the signals. To estimate backgrounds under the signals the numbers of background events are obtained in the same mass windows.

We tested the signal reconstruction efficiencies for various angular distributions in the $N \to {{W}^{ \pm }}{{\ell }^{ \mp }}$ decay. Signal events are generated assuming uniform and different linear cos($\theta _{\ell }^{ \star }$) distributions. The efficiencies obtained after all cuts are approximately the same for all options within the ±5% interval. This follows from the fact that the acceptances and the reconstruction efficiencies of the lepton and W boson produced in the decay are similar.

Finally, the upper limits on the mixing parameters ${\text{|}}{{V}_{{\ell N}}}{{{\text{|}}}^{2}}$ as a function of $M(N)$ are calculated (Fig. 5). The upper limits are obtained assuming $2\sigma$ signal under the background level but not less than the 8 signal events. The decay branching fractions $Br(N\, \to \,{{W}^{ + }}{{\ell }^{ - }})$ are not known and we normalized the obtained upper limits to this value. It has to be noted, that the HNL can potentially decay in the modes $N \to {{W}^{ + }}{{e}^{ - }}$ and $N \to {{W}^{ + }}{{\mu }^{ - }}$. If the both modes are used in analysis, an additional suppression of the boson fusion induced background is expected, however this effect is small.

Fig. 5.

(Color online) Upper limits on the mixing parameters ${\text{|}}{{V}_{{\ell N}}}{{{\text{|}}}^{2}}$ versus $M(N)$ for different HNL masses and CM energies and beams.

As we can see in Fig. 5, the upper limits obtained in the process ${{e}^{ + }}{{e}^{ - }} \to N{{W}^{ \pm }}{{e}^{ \mp }}$ at 1 TeV are somewhat worse than the ones obtained in the process ${{e}^{ + }}{{e}^{ - }} \to N{{\nu }_{e}}$ [11]. However, the upper limits for the process ${{\mu }^{ + }}{{\mu }^{ - }} \to N{{W}^{ \pm }}{{\mu }^{ \mp }}$ are competitive at 3 TeV and overtake the process ${{\mu }^{ + }}{{\mu }^{ - }} \to N{{\nu }_{\mu }}$ [18] at 10 TeV [18–20]. In these publications the current and future LHC upper limits on the mixing parameters are also shown.

4. CONCLUSIONS

Using the model-independent approach for an analysis of SM lepton sector extension by Majorana neutrinos, the process ${{\ell }^{ + }}{{\ell }^{ - }} \to N{{W}^{ \pm }}{{\ell }^{ \mp }}$ is studied and the upper limits on the mixing parameters ${\text{|}}{{V}_{{\ell N}}}{{{\text{|}}}^{2}}$ are obtained as a function of $M(N)$ for different HNL masses and CM energies and beams. The studied process can provide very competitive upper limits, especially at the multi-TeV CM energies.

Similar processes can be used to obtain upper limits also in case of the same-sign beams, in particular in the process ${{\mu }^{ + }}{{\mu }^{ + }} \to N{{W}^{ + }}{{\mu }^{ + }}$. In case of the same-sign beams the signal cross section and event kinematics are exactly the same, resulting in the same number of the signal events. However, the backgrounds are expected to be very small, that should provide slightly better upper limits on the mixing parameters.