INTRODUCTION

Transition metals compounds with high oxidation state often reveal anomalous properties with a rich phase diagram, like for example in trivalent nickel in RNiO3 [1] and tetravalent iron in CaFeO3 [2]. There one observes metal–insulator transitions, charge ordering and unusual types of antiferromagnetic ordering. Charge disproportionation in charge ordered states formally corresponds to appearance of even higher oxidation states Ni+4 and Fe+4. All those anomalies are usually ascribed to significant contribution of oxygen orbitals to formally d-states of transition metals.

Chemically those high oxidation compounds are also very unusual. They are often unstable and can be used as strong oxidizers. The high formal metal ion charges look strange because it takes very large energy to create such ions. The most interesting example of this class is KMnO4 where the formal valence of manganese ion is Mn+7. To make such highly charged ion one needs ~119 eV [3], while energies of chemical bonds are below ~10 eV.

In this paper we present electronic structure calculations for this compound and analyze it using the formalism of Wannier function (WF). Our conclusion is that the chemical bond in \({\text{MnO}}_{4}^{ - }\) complex is strongly covalent and charge transfer between d-states of manganese to p-states of oxygen is small in spite of very large formal oxidation state. Also, our calculations give the number of d-electrons on Mn ion 5.25 that is more appropriate to ionic charge +2 rather than +7.

The paper is organized as follows. First, we describe the methodology used. The way of obtaining the atomic-centered localized Wannier wavefunctions from DFT calculation is presented, then, using these wavefunctions, expressions for ionic and covalent components of the bonding energy in crystal are derived in a general form. Then we define the transformation of basis wavefunctions to make them “natural,” i.e., representing the local crystal structure symmetry of the ions. In the last part of the paper we apply presented methodology to the KMnO4 and show how the interactions within the \({\text{MnO}}_{4}^{ - }\) cluster could be described with four 2 × 2 matrices.

WANNIER FUNCTIONS

Electronic structure calculations were performed using Quantum ESPRESSO package. WFs used for our analysis are the most general and natural choice for definition a set of localized atomic orbitals as electronic states that are formally equivalent to the set of itinerant Bloch functions set. The transformation between them can be considered as unitary transformation in Hilbert functional space. The localization degree and the symmetry of such wave functions could be controlled in the projection procedure. One of the most widespread procedures is an enforcement of maximum localization of WF [4]. The second one [5], successfully used before [6, 7] for describing a plethora of compounds, is a constraint of the WF symmetry to be the same as the symmetry of pure atomic d-orbitals.

In the present paper the second type of projection procedure is used. WFs were generated as projections of the pseudoatomic orbitals \({\text{|}}\phi _{n}^{{\mathbf{k}}}\rangle = \sum\nolimits_{\mathbf{T}} {{e}^{{i{\mathbf{kT}}|\phi _{n}^{{\mathbf{T}}}\rangle }}}\) onto a subspace of the Bloch functions \({\text{|}}\Psi _{\mu }^{{\mathbf{k}}}\rangle \) (the detailed description of WFs construction procedure within pseudopotential method is given in [8]):

$${\text{|}}W_{n}^{{\mathbf{T}}}\rangle = \frac{1}{{\sqrt {{{N}_{k}}} }}\sum\limits_{\mathbf{k}} {\kern 1pt} {\text{|}}W_{n}^{{\mathbf{k}}}\rangle {{e}^{{ - i{\mathbf{kT}}}}},$$
(1)

where

$${\text{|}}W_{n}^{{\mathbf{k}}}\rangle \equiv \sum\limits_{\mu = {{N}_{1}}}^{{{N}_{2}}} {\text{|}}\Psi _{\mu }^{{\mathbf{k}}}\rangle \langle \Psi _{\mu }^{{\mathbf{k}}}{\text{|}}\phi _{n}^{{\mathbf{k}}}\rangle .$$
(2)

Here, \({\mathbf{T}}\) is the lattice translation vector. The resulting WFs \({\text{|}}W_{n}^{{\mathbf{T}}}\rangle \) have symmetry of the atomic orbitals \({{\phi }_{n}}\) positioned at the unit cell defined by \({\mathbf{T}}\) and describe electronic states that form energy bands numbered from \({{N}_{1}}\) to \({{N}_{2}}\).

One can redefine Hamiltonian and density matrix operators in WF basis set:

$$\begin{gathered} \widehat H = \sum\limits_{\mathbf{k}} \sum\limits_{ij} {\kern 1pt} {\text{|}}W_{i}^{{\mathbf{k}}}\rangle H_{{ij}}^{{\mathbf{k}}}\langle W_{j}^{{\mathbf{k}}}{\text{|}}, \\ \widehat \rho = \sum\limits_{\mathbf{k}} \sum\limits_{ij} {\kern 1pt} {\text{|}}W_{i}^{{\mathbf{k}}}\rangle Q_{{ij}}^{{\mathbf{k}}}\langle W_{j}^{{\mathbf{k}}}{\text{|}}. \\ \end{gathered} $$
(3)

Then electron energy E is

$$\begin{gathered} E = {\text{Tr}}(\widehat \rho \widehat H) = \sum\limits_{\mathbf{k}} \sum\limits_{ij} Q_{{ij}}^{{\mathbf{k}}}H_{{ji}}^{{\mathbf{k}}} \\ = \sum\limits_{\mathbf{k}} \sum\limits_i Q_{{ii}}^{{\mathbf{k}}}H_{{ii}}^{{\mathbf{k}}} + \sum\limits_{\mathbf{k}} \sum\limits_{ij,i \ne j} Q_{{ij}}^{{\mathbf{k}}}H_{{ji}}^{{\mathbf{k}}}. \\ \end{gathered} $$
(4)

To separate electron energy E in Eq. (4) into covalent and ionic parts is not a trivial task. While interatomic term \(\sum\nolimits_{\mathbf{k}} \sum\nolimits_{ij,i \ne j} Q_{{ij}}^{{\mathbf{k}}}H_{{ji}}^{{\mathbf{k}}} = \sum\nolimits_{ij,i \ne j} {{E}_{{ij}}}\) is clear a covalent energy, the diagonal in atomic indexes term \(\sum\nolimits_i {{E}_{{ii}}} = \sum\nolimits_{\mathbf{k}} \sum\nolimits_i Q_{{ii}}^{{\mathbf{k}}}H_{{ii}}^{{\mathbf{k}}}\) contains both contributions: covalent energy for all atoms type i in crystal and ionic part of energy. To separate them we have introduced average energy \({{H}_{i}} = \sum\nolimits_{\mathbf{k}} H_{{ii}}^{{\mathbf{k}}}\) and average occupancy \({{Q}_{i}} = \sum\nolimits_{\mathbf{k}} Q_{{ii}}^{{\mathbf{k}}}\) for atom i. The ionic part can be defined as \(E_{i}^{{{\text{ion}}}} = {{Q}_{i}}{{H}_{i}}\) and covalent part as \(E_{i}^{{{\text{cov}}}} = {{E}_{{ii}}} - {{Q}_{i}}{{H}_{i}}\). The electron energy E in Eq. (4) can be written as

$$E = {{E}^{{{\text{cov}}}}} + {{E}^{{{\text{ion}}}}},$$
$${{E}^{{{\text{ion}}}}} = \sum\limits_i E_{i}^{{{\text{ion}}}} = \sum\limits_i {{Q}_{i}}{{H}_{i}},$$
(5)
$${{E}^{{{\text{cov}}}}} = \sum\limits_{ij,i \ne j} {{E}_{{ij}}} + \sum\limits_i {{E}_{{ii}}} - \sum\limits_i {{Q}_{i}}{{H}_{i}}.$$

In a general case with orbital indices \(L = (l,m)\) Eq. (4) is

$$\begin{gathered} E = {\text{Tr}}(\widehat \rho \widehat H) = \sum\limits_{\mathbf{k}} \sum\limits_{iL,jL'} Q_{{iL,jL'}}^{{\mathbf{k}}}H_{{jL',iL}}^{{\mathbf{k}}} \\ = \sum\limits_{\mathbf{k}} \sum\limits_{iL,iL'} Q_{{iL,iL'}}^{{\mathbf{k}}}H_{{iL',iL}}^{{\mathbf{k}}} + \sum\limits_{\mathbf{k}} \sum\limits_{iL,jL'} Q_{{iL,jL'}}^{{\mathbf{k}}}H_{{jL',iL}}^{{\mathbf{k}}}. \\ \end{gathered} $$
(6)

For binary compound \(AB\)

$${{E}_{{{\text{ion}}}}} = {{H}_{A}}{{Q}_{A}} + {{H}_{B}}{{Q}_{B}}.$$
(7)

Chemical bonding energy is

$${{E}_{{{\text{bond}}}}} = {{E}_{{AB}}} - (E_{A}^{\infty } + E_{B}^{\infty })$$
(8)
$$ = {{E}_{{{\text{cov}}}}} + {{E}_{{{\text{ion}}}}} - (H_{A}^{\infty }Q_{A}^{\infty } + H_{B}^{\infty }Q_{B}^{\infty }).$$
(9)

The following approximation could be useful

$$H_{A}^{\infty } = {{H}_{A}} = \sum\limits_{\mathbf{k}} H_{{AA}}^{{\mathbf{k}}},$$
$$H_{B}^{\infty } = {{H}_{B}} = \sum\limits_{\mathbf{k}} H_{{BB}}^{{\mathbf{k}}}.$$
(10)

Then, from Eqs. (8) and (5):

$${{E}_{{{\text{bond}}}}} = {{E}_{{{\text{cov}}}}} + {{E}_{{{\text{ion}}}}} - ({{H}_{A}}Q_{A}^{\infty } + {{H}_{B}}Q_{B}^{\infty }),$$
$${{E}^{{{\text{ion}}}}} = E_{A}^{{{\text{ion}}}} + E_{B}^{{{\text{ion}}}} = {{Q}_{A}}{{H}_{A}} + {{Q}_{B}}{{H}_{B}},$$
(11)
$${{E}^{{{\text{cov}}}}} = 2{{E}_{{AB}}} + {{E}_{{AA}}} - {{Q}_{A}}{{H}_{A}} + {{E}_{{BB}}} - {{Q}_{B}}{{H}_{B}}.$$

Hence bonding energy separation is:

$${{E}_{{{\text{bond}}}}} = E_{{{\text{bond}}}}^{{{\text{cov}}}} + E_{{{\text{bond}}}}^{{{\text{ion}}}},$$
(12)
$$E_{{{\text{bond}}}}^{{{\text{ion}}}} = E_{A}^{{{\text{ion}}}} + E_{B}^{{{\text{ion}}}} - ({{H}_{A}}Q_{A}^{\infty } + {{H}_{B}}Q_{B}^{\infty })$$
$$ = ({{Q}_{A}} - Q_{A}^{\infty }){{H}_{A}} + ({{Q}_{B}} - Q_{B}^{\infty })){{H}_{B}},$$
(13)
$$E_{{{\text{bond}}}}^{{{\text{cov}}}} = {{E}^{{{\text{cov}}}}} = 2{{E}_{{AB}}} + {{E}_{{AA}}} - {{Q}_{A}}{{H}_{A}} + {{E}_{{BB}}} - {{Q}_{B}}{{H}_{B}}.$$

Occupation matrix and natural orbitals basis. Occupation matrix \(Qij\) in Eq. (3) has in general except atomic number indexes \(i,j\) also orbital indexes \(L,L{\kern 1pt} '\) where \(L = (lm)\) is combined index with l orbital moment quantum number and its projection m. The WF \({\text{|}}{{W}_{i}}\rangle \) is obtained in Eq. (1) by projection on Bloch functions \({\text{|}}\psi _{{\mathbf{k}}}^{\alpha }\rangle \) trial atomic wave function \({\text{|}}{{\phi }_{i}}\rangle \). These atomic orbitals have in general in addition to atomic number also orbital indices \({\text{|}}{{\phi }_{{iL}}}\rangle \) and hence resulting WFs are \({\text{|}}{{W}_{{iL}}}\rangle \). So, density matrix and Hamiltonian in Eq. (3) has the following form:

$$\begin{gathered} \widehat H = \sum\limits_{iL,jL'} {\text{|}}{{W}_{{iL}}}\rangle {{H}_{{iL,jL'}}}\langle {{W}_{{jL'}}}{\text{|}}, \\ \widehat \rho = \sum\limits_{iL,jL'} {\text{|}}{{W}_{{iL}}}\rangle {{Q}_{{iL,jL'}}}\langle {{W}_{{jL'}}}{\text{|}}. \\ \end{gathered} $$
(14)

Hence for atomic “diagonal” term \(i = j\) one in general has nondiagonal \(L,L{\kern 1pt} '\) occupation matrix \({{Q}_{{iL,iL'}}}\). It would be convenient to choose the “natural” atomic orbital basis set where atomic occupation matrix is diagonal. Also, it is useful to choose special linear combination of ligand-atoms orbital having the same symmetry as atomic orbital of the metallic ion. That can be done by diagonalization of the matrix

$$\widetilde Q = UQ{{U}^{\dag }}.$$
(15)

Here, \(U\) is unitary atomic basis transformation matrix

$${\text{|}}{{\widetilde \phi }_{{iL}}}\rangle = \sum\limits_{L'} {{U}_{{L,L'}}}{\text{|}}{{\phi }_{{iL'}}}\rangle .$$
(16)

These “natural” atomic orbitals \({\text{|}}{{\widetilde \phi }_{{iL}}}\rangle \) have usually the form corresponding to basis functions of irreducible representation for crystal structure symmetry group.

CALCULATION RESULTS

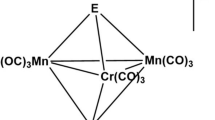
KMnO4 crystallizes in the orthorhombic P\(mmn\) space group with unit cell parameters \(a = 5.93{\kern 1pt} \) Å, \(b = 7.58{\kern 1pt} \) Å, \(c = 9.23{\kern 1pt} \) Å [9]. In potassium permanganate, the manganese ion is surrounded by four oxygens ions with a tetrahedral environment corresponding to the Td point group symmetry (see Fig. 1). For this symmetry five d-orbitals transform according to triply degenerate irreducible representation \({{t}_{{2g}}}\) (orbitals xy, \(xz,yz\)) and doubly degenerate representation \({{e}_{g}}\) (orbitals \(3{{z}^{2}} - {{r}^{2}}\) and \({{x}^{2}} - {{y}^{2}}\)). In contrast to the octahedral symmetry Oh \({{t}_{{2g}}}\) level lies higher in energy than \({{e}_{g}}\) level.

Fig. 1.
figure 1

(Color online) Crystal structure of KMnO4 consists of MnO4 tetrahedra and potassium atoms between them.

Full size image

Resulting energy bands dispersion (Fig. 2) and density of states (Fig. 3) show rather narrow bands in agreement with well separated \({\text{MnO}}_{4}^{ - }\) ions in the structure. The partial density of the states in Fig. 3 showing the contribution of manganese d-orbitals and oxygen p‑orbitals to various bands clearly indicates two antibonding sets of \(d{\kern 1pt} - {\kern 1pt} p\) bands around 1 and 3 eV energy of \({{e}_{g}}\) and \({{t}_{{2g}}}\) symmetry. The corresponding bonding counterpart of the same symmetry bands can be observed at –5 eV. The set of bands between –4 and ‒1 eV has pure oxygen p-character and corresponds to a non-bonding combination of p-orbitals that do not hybridize with metallic d-states.

Fig. 2.
figure 2

(Color online) Band structure of KMnO4.

Full size image
Fig. 3.
figure 3

(Color online) Density of states of KMnO4.

Full size image

In order to analyze spatial distribution of electronic states in this material we have calculated squared modulus of WFs for unoccupied bands (marked by red on Fig. 2). The results are presented in Fig. 4. These figures show spatial distribution of holes for various symmetry states of \({\text{MnO}}_{4}^{ - }\) ion. As one can easily see, nearly half of the hole density for every WF is situated on the neighboring oxygen ions. The Table 1 shows percentage of Mn-d and O-p contributions to the WF charge representing holes in formally \({{d}^{0}}\) shell of manganese ion. It is clear that in fact more than half of each ten formally d holes in reality belong to the oxygen states. The total number of d-holes from this table gives 4.54 which corresponds to the number of d-electrons 5.46. That agrees well with the occupancy of manganese d-shell 5.25 obtained in full DFT calculations. So, while formal valency of metal in this compound is seven the occupancy of d-shell corresponds rather to Mn+2 with admixture of Mn+.

Fig. 4.
figure 4

(Color online) Wannier functions (isosurface of the squared moduli) with the symmetry of manganese d-orbitals.

Full size image
Table 1. Contribution of atomic states to Wannier functions of KMnO4
Full size table

Keeping in mind that in KMnO4 there is an ionic type of bonding between potassium and \({\text{MnO}}_{4}^{ - }\) ions, we calculated the contribution of covalent and ionic parts to the chemical bond within the \({\text{MnO}}_{4}^{ - }\) complex according to Eq. (12). The obtained values \(E_{{{\text{bond}}}}^{{{\text{cov}}}} = - 38.2\) eV and \(E_{{{\text{bond}}}}^{{{\text{ion}}}} = 0.07\) eV confirm that \({\text{MnO}}_{4}^{ - }\) ion in KMnO4 is a totally covalent complex. Below we map the picture of chemical bonding in KMnO4 on a simple model.

DISCUSSION

Chemical bond is a basic concept of chemistry. A bond holds atoms in a molecule together by sharing their electrons on molecular orbitals obtained as a combination of hybridized atomic orbitals. In crystal there are no atomic orbitals anymore but its electrons are described by Bloch wave functions \({\text{|}}\Psi _{\mu }^{{\mathbf{k}}}\rangle \) that are spread over the whole crystal. WF formalism was developed in order to construct atomic-like functions centered on specific atoms and having the corresponding symmetry. This is done by unitary transformation of Bloch functions Hilbert space into new WF basis via Eqs. (1) and (2).

In the simplest case of a single bond for binary compound AB we can write rather simple Hamiltonian matrix in WF basis. It can describe both covalent and ionic parts of chemical bond. The most important parameters in our WF formalism are \({{H}_{A}},{{H}_{B}}\)—atomic energies (diagonal terms of the Hamiltonian) or their difference \(\Delta E = {{H}_{A}} - {{H}_{B}}\) and off-diagonal Hamiltonian matrix terms \({{H}_{{AB}}} = t\) determining electron hopping between atoms. The first one \(\Delta E\) defines the tendency to form ions from neutral atoms and the second one \(t\) forms a covalent bond between atoms. It would be useful to consider the simplest model containing those parameters and compare with it our calculation results.

Let’s assume that A and B are two different atoms with one partially filled nondegenerate orbital on each ion (2 electrons total). The Hamiltonian of the system is then:

$$H = \left( {\begin{array}{*{20}{c}} E&t \\ t&{E - \Delta E} \end{array}} \right),$$
(17)

where E is the energy level of the first orbital (the higher one) and second ion has the orbital energy on \(\Delta E\) lower than the first one. The hopping energy term t corresponds to hybridization between the orbitals. From the eigenvectors of the model Hamiltonian (Eq. (17)) one can get occupation numbers for the two atoms (A and B) orbitals (\({{Q}_{1}}\) and \({{Q}_{2}}\)) and then calculate the charge transfer \({{Q}_{2}} - {{Q}_{1}}\) from the first to the second atom. One can easily see that larger \(t{\text{/}}\Delta E\) value give smaller charge transfer value \({{Q}_{2}} - {{Q}_{1}}\) that characterizes ionicity and hence the chemical bond in the system will be more covalent. On the contrary if the value of \(t{\text{/}}\Delta E\) parameter is small then the opposite is true and the system will be characterized by mostly ionic bond.

The ionicity can be calculated from \({{Q}_{2}} - {{Q}_{1}}\) in the following way: \({{I}_{1}} = Q_{1}^{{{\text{inf}}}} - {{Q}_{1}}\), \({{I}_{2}} = - {{I}_{1}}\), \({{I}_{2}} = ((Q_{2}^{{{\text{inf}}}} - \) \(Q_{1}^{{{\text{inf}}}}) - ({{Q}_{2}} - {{Q}_{1}})){\text{/}}2\), where \(Q_{1}^{{{\text{inf}}}}\) and \(Q_{2}^{{{\text{inf}}}}\) are occupations for the corresponding neutral atoms A and B (for our simple model \(Q_{1}^{{{\text{inf}}}} = Q_{2}^{{{\text{inf}}}} = 1).\)

To analyze chemical bonding in KMnO4 we have redefined the basis of WFs for complex ion (MnO4)– to make it as similar as possible to the two orbital bonding model. To achieve that, one needs for every Mn-d orbital to find a set of oxygen p-orbitals that hybridizes most with the specific Mn-d one.

For each \({\text{MnO}}_{4}^{ - }\) complex in the cell we constructed five linear combinations of the 12 O-p orbitals in such a way, that every such set transforms according to the same irreducible representation of the Mn-ion point group Td as one of the Mn-d orbitals. Consequently, we have got the five pairs of d- and p-type orbitals that are mostly hybridized (within the pair) by symmetry. Corresponding 10 orbitals will form chemical bonding within the \({\text{MnO}}_{4}^{ - }\) cluster. Additionally, we constructed another 7 linear combinations of the O-p orbitals that are orthogonal to the five linear combinations described above. These 7 orbitals represent the non-bonding oxygen states of the \({\text{MnO}}_{4}^{ - }\) cluster.

In this way we have separated full 17-dimensional linear space of d-Mn and p-oxygen orbitals of \({\text{MnO}}_{4}^{ - }\) ion into two orthogonal subspaces: 7-dimensional non-bonding oxygen orbital subspace and 10-dimensional subspace responsible for chemical bonding in this system. The first orbitals subspace forms a set of non-bonding bands between –4 eV and –1 eV (see Figs. 2 and 3) and the second one forms bonding bands at –5 eV and antibonding ones from \(1\) to 3 eV.

Those 17 orbitals were used to build 17 WFs that describe all occupied and empty energy bands, i.e., all bands within the \([ - 6;4]{\kern 1pt} \) eV energy interval corresponding to (MnO4)– ion. The separation of the electron states into bonding and non-bonding subspaces is clear (Figs. 2 and 3). We have calculated within this new basis the Hamiltonian matrix and the occupation matrix (see Appendix where we have omitted not essential for our analysis non-bonding states terms). These 10 × 10 matrices, due to the presence of the rather high symmetry of the \({\text{MnO}}_{4}^{ - }\) tetrahedra, could be constructed by doubly degenerate 2 × 2 matrices describing interaction of the Mn-\({{e}_{g}}\) states with the O‑p bonding orbital and triply degenerate 2 × 2 matrices for the Mn-\(t2g\) states and the corresponding O‑p bonding orbitals

$$H_{{ij}}^{{{{e}_{g}}}} = \left( {\begin{array}{*{20}{c}} {0.59}&{ - 2.97} \\ { - 2.97}&{0.9} \end{array}} \right),\quad Q_{{ij}}^{{{{e}_{g}}}} = \left( {\begin{array}{*{20}{c}} {0.53}&{0.5} \\ {0.5}&{0.48} \end{array}} \right),$$
$$H_{{ij}}^{{{{t}_{{2g}}}}} = \left( {\begin{array}{*{20}{c}} {1.49}&{ - 3.90} \\ { - 3.90}&{1.56} \end{array}} \right),\quad Q_{{ij}}^{{{{t}_{{2g}}}}} = \left( {\begin{array}{*{20}{c}} {0.51}&{0.5} \\ {0.5}&{0.5} \end{array}} \right).$$

This means that a 10 × 10 dimensional bonding orbital space is essentially formed by five orthogonal 2 × 2 dimensional subspaces. Every one of them can be described by the simple model Eq. (17). Diagonalizing those Hamiltonian matrices one obtains eigenvalues 3.72 and –2.23 for \({{t}_{{2g}}}\) states and 5.48 and –2.43 for \({{e}_{g}}\) states that corresponds perfectly with position of bonding and antibonding bands of Fig. 3. The corresponding occupations matrices give \({{Q}_{2}}\) and \({{Q}_{1}}\) values very close to 0.5 and their difference \({{Q}_{2}} - {{Q}_{1}}\) is nearly zero. That means almost completely prefect covalent bond for \({\text{MnO}}_{4}^{ - }\) ions and practical absence of the ionic contribution to the bonding. The value of \(t{\text{/}}\Delta E\) is equal 0.10 for \({{e}_{g}}\) states and 0.02 for \({{t}_{{2g}}}\) states. That agrees well with our conclusion of nearly pure covalent bond in \({\text{MnO}}_{4}^{ - }\) ion.

To summarize, we have calculated electronic structure for KMnO4 compound with formally seven valency Mn ion and analyzed the results with WF formalism. We have found the chemical bond in \({\text{MnO}}_{4}^{ - }\) complex being nearly of perfect covalent type with practically no presence of ionic contribution. The d‑electors charge distribution for Mn atom corresponds to charge close to +2 rather than the formal ionic charge of +7.