Multiphoton and tunneling ionization of atoms and molecules in intense laser fields has been observed experimentally since the mid-1960s [1]. Shortly after the discovery of multiphoton absorption of high-power laser radiation, an essentially nonlinear interaction regime was observed, in which the number of photons involved in each ionization event exceeds the minimum required for the transition to the continuum [2]. The theory of nonlinear ionization in the field of a plane electromagnetic wave was formulated in [3–6], where analytical formulas for the ionization rate and momentum distributions of photoelectrons were derived within the strong field approximation, when the Coulomb interaction of the emitted electron with the atomic residual is not accounted for. The Coulomb factor in the ionization rate was found in [7] in the limit of a slowly varying field, and then in [8] for an arbitrary laser frequency. The results obtained in the pioneering works [3–7] were significantly advanced in the subsequent decades. At present, the theory of nonlinear ionization of atoms and molecules is widely used to describe the effects of the interaction of high-power laser radiation with matter. The current state of the art in the theory of multiphoton and tunneling ionization of atomic systems in strong fields is presented in reviews [9–14].

As the maximal intensity of laser radiation increases, the study of the ionization of deep levels of heavy atoms and multiply charged ions becomes topical. Such processes are interesting in particular in view of their possible use for direct measurement of the laser intensity at the focus (see [15–17] and references therein). Besides, the possibility of observing relativistic effects in ionization is of fundamental interest. The photoelectron motion in a laser field becomes relativistic at:

$${{a}_{0}} = \frac{{e{{E}_{0}}}}{{mc\omega }} > 1.$$
(1)

Here, \({{E}_{0}}\) and ω are the amplitude and frequency of the laser wave, m and e are the electron mass and the absolute value of its charge, respectively; c is the speed of light. In the following, atomic units \(e = m = \hbar = 1\) are used with \(c = 137\). For infrared laser fields with wavelengths \(\lambda \approx 1{\kern 1pt} \) μm and \(\omega \approx 0.045\), this relativistic threshold is reached at \(J \approx 2 \times {{10}^{{18}}}\) W/cm2. Kinematic effects in the spectra of photoelectrons and of radiation emitted by these electrons are well studied (see, for example, [18–20] and references therein). At intensities \(J \simeq {{10}^{{18}}}{-} {{10}^{{21}}}\) W/cm2 currently available at many laser facilities, photoelectrons quickly become relativistic after ionization, although the process of their detachment from an atom remains determined by the laws of non-relativistic quantum mechanics, and ionization rates can be calculated with high accuracy using formulas from [3, 5–7]. This extension of the applicability of the nonrelativistic theory into the domain of ultrarelativistic intensities is mainly due to the fact that the binding energies of the levels ionized in such fields remain small compared to the rest energy of the electron. As a result, relativistic corrections to the sub-barrier electron trajectory and the respective corrections to the ionization probability appear minor even at intensities \(J \simeq {{10}^{{23}}}\) W/cm2.

At intensities \(J{{ > 10}^{{23}}}\) W/cm2, currently available or expected to achieve in the coming years with new multi-petawatt laser systems [21–24], the probability of the electron detachment from an atom is determined not only by the electric but also by the magnetic field of the laser wave, and relativistic corrections to the electron trajectory become significant during the process of transition from the bound state to the continuum. Qualitatively, the regime of this transition is determined by the value of the Keldysh parameter [3]:

$$\gamma = \frac{{\sqrt {2{{I}_{p}}} \omega }}{{{{E}_{0}}}}.$$
(2)

At \(\gamma \gg 1\), ionization can be considered as multiphoton absorption, while in the opposite limit \(\gamma \ll 1\) it is described as tunneling through a slowly varying potential barrier. As the laser intensity \(J \sim E_{0}^{2}\) increases, the effective value of the Keldysh parameter \({{\gamma }_{*}}\), upon reaching which the level is rapidly ionized, decreases as \({{\gamma }_{*}} \sim E_{0}^{{ - 2/3}}\). For lasers with a wavelength of \(\lambda \approx \) 1 μm and atoms in the ground state, the tunneling regime is reached starting from about \(J \approx 5 \times \) 1014 W/cm2. Thus, at record intensities >1023 W/cm2 considered in this work, ionization proceeds in a deep tunneling regime, \(\gamma \simeq {{10}^{{ - 2}}}{-} {{10}^{{ - 3}}}\) making it possible to use the constant field approximation to calculate the ionization probability with a very high accuracy. Presently, for the first time, conditions arise for the experimental observation of the relativistic tunneling effect in atoms.

The theory of ionization of atoms in fields of relativistic intensity determined by the condition (1) was first formulated in [4]. Relativistic tunneling effect was theoretically studied in [25, 26], as well as in a number of other later works (see reviews [13, 27] and references therein). These papers show that the probability of ionization of a deep-lying atomic level, whose energy is determined taking into account relativistic corrections, can differ significantly, by several orders of magnitude, from that calculated by non-relativistic formulas [5–7]. The ratio of ionization rates calculated by non-relativistic and relativistic formulas can be both greater or less than unity [9]. In a recent paper [28], this point was investigated in more detail, and it was shown that the effect of a magnetic field on the probability of tunneling in heavy ions, associated with the Zeeman splitting of levels, can be detected at intensities \(J > 2 \times {{10}^{{23}}}\) W/cm2. To find effects associated with relativistic corrections to the sub-barrier motion of an electron, even higher intensities exceeding 1024 W/cm2 are needed. Achieving such intensities will become possible, in particular, by superimposing several multi-petawatt laser beams in the focal region. Such a scheme for obtaining extreme light fields is proposed at the XCELS [21] facility, which is currently under construction. The maximal number of beams is 12 at a power of 15 PW in each beam. In the electromagnetic field that arises when the laser beams cross, the electric E and magnetic H fields are no longer equal in amplitude and can also be non-orthogonal. Expressions for the probability of the relativistic tunneling effect in a static electromagnetic field of various configurations were obtained in [25, 26] and can be used, after necessary generalizations, to analyze possible multibeam experiments. In this paper, we present such an analysis for the case of ionization of the s-states of multiply charged ions in the field of two crossed laser beams, i.e., the simplest multibeam configuration that can be implemented at the XCELS facility. It is shown that for a fixed power of each of the beams, the most significant relativistic effect can be achieved using the counter-propagating geometry.

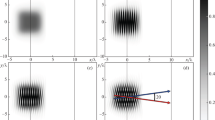
Let us consider the field resulting from a coherent overlap of two laser beams linearly polarized in the same direction. Describing each of the beams in the plane wave approximation with the same amplitude values of electric \({{{\mathbf{E}}}_{0}}\) and magnetic fields \({{{\mathbf{H}}}_{{0i}}} = {{{\mathbf{n}}}_{i}} \times {{{\mathbf{E}}}_{0}}\), \(i = 1,2\), where \({{{\mathbf{n}}}_{i}} = {{{\mathbf{k}}}_{i}}{\text{/}}{{k}_{i}}\) are unit vectors specifying the directions of wave propagation, and \({{{\mathbf{k}}}_{i}}\) are the wave vectors, we obtain that the maximum value of the electric field is \({{E}_{m}} = 2{{E}_{0}}\). In this case, the magnetic field amplitude is \({{H}_{m}} = 2{{E}_{0}}\cos \theta \). Here θ is the half angle between the directions of the wave vectors. The electric and magnetic fields remain orthogonal. Taking into account the highly nonlinear dependence of the ionization rate on the electric field strength, we examine this quantity in those parts of the focus that will make a dominant contribution to the formation of multiply charged ions. These are parts of space where the amplitude of the electric field is maximum.

Consider tunneling from an s-state of a multiply charged ion with an ionization potential \({{I}_{p}}\). In this case, there are no linear Zeeman shifts in the magnetic field, and the spin effects remain insignificant even in extremely strong fields [29]. In the semiclassical approximation [9, 25, 26], the ionization rate can be presented in the form

$$w \sim \exp \{ - 2{\text{Im}}{{S}_{0}}\} ,$$
(3)

where the classical action \({{S}_{0}}\) is calculated along the trajectory corresponding to the zero electron velocity at the barrier exit at \(t = 0\):

$$\begin{gathered} {{S}_{0}} = \int\limits_{{{t}_{0}}}^0 (L + {{c}^{2}} - {{I}_{p}})dt , \\ L = - {{c}^{2}}\sqrt {1 - \frac{{{{v}^{2}}}}{{{{c}^{2}}}}} + \frac{1}{c}({\mathbf{Av}}) - \varphi . \\ \end{gathered} $$
(4)

Here, φ and A are the scalar and vector potentials specifying the electromagnetic field of the laser wave, and the complex time instant \({{t}_{0}}\) of the motion start is determined from the condition that the initial energy of the photoelectron is equal to that of the bound state. When the condition \(\gamma \ll 1\) is satisfied, the time of sub-barrier motion is a small fraction of the optical period, \({\text{|}}\omega {{t}_{0}}{\text{|}} \ll 1\), and the field can be treated as constant; in this case \(\varphi = - {{{\mathbf{E}}}_{0}}{\mathbf{r}}\), \({\mathbf{A}} = ({{{\mathbf{H}}}_{{01}}} + {{{\mathbf{H}}}_{{02}}}) \times {\mathbf{r}}{\text{/}}2\). The electron trajectory satisfies the equations of motion in complex time with the Lorentz force, and \({{t}_{0}}\) is determined from the equation:

$$\frac{1}{{\sqrt {1 - {{v}^{2}}({{t}_{0}}){\text{/}}{{c}^{2}}} }} = 1 - \frac{{{{I}_{p}}}}{{{{c}^{2}}}} .$$
(5)

Omitting the details of calculations, part of them are contained in [25, 26], we present a result applicable at \({{I}_{p}} \ll {{c}^{2}}\):

$${{w}_{{\text{R}}}}(t) = {{w}_{{{\text{NR}}}}}(t)\exp \left\{ {\frac{1}{{F(t)}}\left( {\frac{1}{{10}} - \frac{2}{{45}}\mathop {\cos }\nolimits^2 \theta } \right)\frac{{{{I}_{p}}}}{{{{c}^{2}}}}} \right\},$$
(6)

where \({{w}_{{{\text{NR}}}}}(t)\) is the nonrelativistic ionization rate [5, 6, 9]. For s-states it is given by

$${{w}_{{{\text{NR}}}}}(t) = {{C}^{2}}{{2}^{{2\nu + 1}}}{{I}_{p}}{{F}^{{1 - 2\nu }}}(t)\exp \left\{ { - \frac{2}{{3F(t)}}} \right\}.$$
(7)

The reduced electric field and the effective quantum number are equal to

$$F(t) = \frac{{E(t)}}{{{{{(2{{I}_{p}})}}^{{3/2}}}}} ,\quad \nu = \frac{Z}{{\sqrt {2{{I}_{p}}} }} ,$$
(8)

Z is the atomic residual charge. The asymptotic coefficient of the single-electron wave function \(C \simeq 1\) at large distances from the atomic core can be determined numerically or using a semiclassical asymptotic [9]. For \(\gamma \ll 1\), time in the formulas (6), (7) can be considered as a parameter. Expressions (6), (7) for the ionization rate are obtained in the semiclassical approximation. Their applicability conditions require that the barrier width \(b \approx {{I}_{p}}{\text{/}}E(t)\) remains large compared to the electron de Broglie wavelength \({{\lambda }_{D}} \simeq 1{\text{/}}\sqrt {{{I}_{p}}} \). This means that the value of the reduced field (8) is \(F \ll 1\). In this case, taking into account the fact that the ionization of deep albeit weakly relativistic levels, \(1 \ll {{I}_{p}} \ll {{c}^{2}}\), is considered, the field strength \(E(t)\) upon reaching which the ionization rate (6) becomes significant, grows as \( \sim {\kern 1pt} {{Z}^{3}}\). Thus, for the \(1s\) state of hydrogen-like xenon with Ip = 41300 eV ≈ 1518 a.u. the value of the reduced field, which provides almost complete ionization in a single period of the laser wave, \(F = 0.05\), is reached at \(E \approx 3.0 \times \) 103 a.u. corresponding to the intensity \(J \approx 3.1 \times \) 1023 W/cm2. Note that for s-levels, where \(\nu \approx 1\), the above-barrier ionization regime [9] is typically not reached [30], and the above given semiclassical formulas (6), (7) remain quantitatively accurate. In the case of ionization of p‑states with \(\nu \approx 2\) it may be necessary to take into account corrections arising due to the suppression of the potential barrier (see [30] and references therein).

We will be interested to analyze the difference between the relativistic and nonrelativistic ionization rates determined by the exponential factor in (6). In particular, the dependence of this exponential factor on the angle \(2\theta \) between the beams will be examined. In [9, 25, 26] a semiclassical expression was obtained for the probability of relativistic tunneling for the case of perpendicular and unequal fields under the condition \({{E}_{m}} < {{H}_{m}}\), which corresponds to Lorentz ionization [31]. Formulas for the opposite case we are interested in \({{E}_{m}} > {{H}_{m}}\) can be obtained from [26] by the method of analytic continuation. A detailed derivation and analysis of a more general case on nonorthogonal fields will be presented elsewhere. The polynomial in the exponent of (6) gives the first term of the expansion of the exact expression for the imaginary part of the action in a small parameter \({{I}_{p}}{\text{/}}{{c}^{2}}\) for the case of orthogonal fields under the condition \({{E}_{m}} > {{H}_{m}}\). This formula is sufficient for making estimates that allow one to establish the conditions necessary for experimental observation of relativistic effects in laser fields of extreme intensity.

In order to formulate these conditions, note the following.

1. The probability of tunneling ionization is a sharp function of the reduced field F, therefore, for a given electron level with an ionization potential \({{I}_{p}}\), tunneling effectively occurs in a narrow range of fields near \(F = 0.03{-} 0.05\) [15]. The value of this interval depends logarithmically on the laser pulse duration, which makes it possible to provide a fairly universal estimate of the field threshold for observing tunneling ionization. At \(F = 0.05\), the complete ionization of levels with any values of the azimuthal and magnetic quantum numbers will occur within one optical period (or even faster) of a laser pulse with a wavelength of \(\lambda = \) 1 μm [15]. For laser pulses with duration of \(\tau = 25\) fs, which corresponds to the planned parameters of the XCELS laser facility, a gas target density of 1015 cm–3 and a focus volume of \( \approx {\kern 1pt} 20{{\lambda }^{3}}\), several tens of ions (a number sufficient for registration of multiply charged ions by modern detectors) will be produced at \(F = 0.02\). When going to \(F = 0.015\), the ionization rate will drop by 5 orders of magnitude so that the probability of generating even one ion per pulse becomes negligible. Thus, the value \(F = 0.02\) can be taken as the lower threshold for the observation of tunneling ionization.

2. The restriction on the reduced field F specifies the maximum value of the binding energy of the level, whose ionization can, in principle, be observed at a certain maximum value of the laser intensity at the focus. Intensities of ~1023 W/cm2 [24] have been achieved so far. With optimistic expectations, intensities of ~1025 W/cm2 can be achieved at 100-petawatt class facilities XCELS in Russia and Station of Extreme Light in China. According to the above estimates, in the field with such an intensity it is possible to observe tunneling from levels with ionization potentials of about 120 keV, which corresponds to the ground states of hydrogen-like radon or thorium ions. In this case \({{I}_{p}}{\text{/}}{{c}^{2}} \approx 0.24\) so that the expansion of the action in this parameter quickly converges, and the approximate expression (6) can be used for estimates.

In the case of two parallel beams, the coefficient in front of \({{I}_{p}}{\text{/}}{{c}^{2}}\) in (6) is \(1{\text{/}}(18F)\), for \(\theta = \pi {\text{/}}4\) (beams propagating orthogonally) \( - 7{\text{/}}(90F)\), and for counter-propagating beams \((\theta = \pi {\text{/}}2)\) – \(1{\text{/}}(10F)\). As a result, in the transition from ionization in two parallel or nearly collinear beams to the case of counter-propagating beams, the ionization rate and the yield of fully ionized atoms with binding energies of \(1{{s}^{1}}\) states of about 100 keV should increase by approximately a factor of 2. The increase in the ionization probability is mainly due to relativistic corrections to the sub-barrier electron trajectory. Thus, an experimental measurement of the increase in the yield of multiply charged ions in the situation described above could be interpreted as an observation of the influence of relativistic effects on tunneling in a strong external field. It should be noted that the laser field intensity remains also ultrarelativistic for \(\theta = 0\), that is, for parallel beam propagation or in the case of a single beam. The relativistic correction to the tunneling probability in this case appears smaller, because the magnetic field deforms the sub-barrier electron trajectory, making it two-dimensional, which leads to an increase in the imaginary part of the action (4) and to the suppression of the ionization probability [26]. Relativistic corrections to the action due to the electric field, on the contrary, increase the probability. In the case of a crossed field, these corrections are almost completely compensated, and the net effect appears strongly suppressed.

As one can see from the above estimates, the relativistic effects in tunneling turn out to be relatively weak even at high intensities [15, 28]. A relativistic enhancement of the ionization probability in the field of a standing wave by an order of magnitude compared to the ionization probability in parallel beams can be expected at intensities \( \simeq {\kern 1pt} {{10}^{{26}}}\) W/cm2, which is hardly possible to achieve in the coming years.

Let us discuss a possible experimental realization. The ion yield must be measured in a rarefied gas jet at concentrations <1015 cm–3, which allow one to avoid the influence of plasma fields, the appearance of bremsstrahlung, and collisional ionization. The requirements to an experimental setup aimed to observe tunneling ionization of deep atomic levels in a strong laser field are described in detail in [32, 33]. The measured value is the number of ions of the maximum charge state depending on the mutual orientation of the beams at fixed energies of the latter. A significant problem for extracting the contribution of relativistic ionization to the yield of ions of the maximum charge state will be the change in the structure of the focus with variation in the angle between the beams. As the angle θ increases, the part of space where the electric field amplitude takes values close to the maximum \(2{{E}_{0}}\) will decrease. This effect may happen to be considerably more significant than the increase in the number of ions due to the suppression of the magnetic field in the counter-propagating beams. The influence of a change in the effective focal volume can be eliminated by measuring the yield of ions of smaller charge at lower intensities, for which relativistic effects are clearly insignificant, and the ionization probability is determined by the amplitude of the electric field only. Thus, an experiment in which the angle between the beams changes from a small value to \(\theta = \pi {\text{/}}4\) (orthogonal beams) and then to \(\theta = \pi {\text{/}}2\) (counter-propagating beams) must be carried out at two values of laser power that ensure the achievement of an intensity of ≈1025 W/cm2, at which hydrogen-like ions Rn and Th are ionized and, for example, at \(J \approx {{10}^{{23}}}\) W/cm2 when the \(2s\) shells of the same atoms are ionized. In the second case, the measured ratio of the number of ions \({{N}^{{(Z - 2) + }}}\) of charge \(Z - 2\) for different angles between the beams, \({{N}^{{(Z - 2) + }}}(\pi {\text{/}}4){\text{/}}{{N}^{{(Z - 2) + }}}(0)\), etc., will then make it possible to calibrate the measurement results for \({{N}^{{Z + }}}\) and to extract the contribution of relativistic effects.

The proposed experiment can also be performed in a scheme with the number of beams >2. Considering that the maximum ionization rate corresponds to the case of a zero magnetic field, such a scheme in its most preferable form should use an even number of mutually counter-propagating beams. Note that the proposed experimental scheme is feasible only at a high degree of coherence of the overlapping beams. It is not yet clear what degree of coherence can be achieved on multi-beam laser systems with multi-petawatt power.