Determination of the Superconducting Order Parameter of BaFe_1.92Ni_0.08As₂ Weakly Underdoped Pnictides by Two Complementary Techniques

The structure of the superconducting order parameter of weakly underdoped BaFe_1.92Ni_0.08As₂ pnictides with the critical temperature T_c ≈ 18.2 K has been determined. Two microscopic superconducting order parameters—the small superconducting gap Δ_S(0) and, supposedly, the edges of the large gap with anisotropy in the ab plane $\Delta _{{\text{L}}}^{{{\text{out}}}}(0)$ and $\Delta _{{\text{L}}}^{{{\text{in}}}}(0)$—have been determined at T ≪ T_c, together with their temperature dependences, using incoherent multiple Andreev reflection spectroscopy. It has been shown that the determined temperature dependence of the lower critical field H_c1(T) can be described in the two-band approximation both within the so-called alpha model (using experimental Δ_S(0), $\Delta _{{\text{L}}}^{{{\text{out}}}}(0)$, and $\Delta _{{\text{L}}}^{{{\text{in}}}}(0)$ values) and using the temperature dependences Δ_S(T) and $\Delta _{{\text{L}}}^{{{\text{out}}{\text{,in}}}}(T)$ obtained by multiple Andreev reflection spectroscopy under the assumption of a fairly strong anisotropy of the small superconducting gap, where the experimental Δ_S(0) value is taken as the outer edge of its angular distribution.

1 INTRODUCTION

Superconducting BaFe₂As₂ pnictides of the Ba-122 family have a layered crystal structure and critical temperatures up to T_c ≈ 21 K at partial substitution Fe_2 – xNi_x at the optimal doping level x = 0.1 [1]. Angle-resolved photoemission spectroscopy (ARPES) reveals embedded hole cylinders on the Fermi surface around the Γ point of the Brillouin zone and electron cylinders around the M point corrugated along the k_z direction [2].

Although ARPES studies of BaFe_2 – xNi_xAs₂ (BFNA) pnictides in the superconducting state have not yet been performed, the general feature of pnictides of the Ba-122 family is the anisotropy of superconducting gaps in the momentum space, which was observed in ARPES experiments [3, 4] and considered theoretically [5, 6]. The calculations of the gap structure for the Ba-122 family [5, 6] show the existence of anisotropic superconducting gaps in both spin-fluctuation (${{s}^{ \pm }}$) and orbital-fluctuation (${{s}^{{ + + }}}$) approaches. The combination of these interaction types [6] makes it possible to obtain various gap structures, including those with the “nodal” order parameter (having nodes in the k space distribution). A new comprehensive method proposed in this work allowed us to obtain reliable experimental data on the anisotropy of superconducting gaps in BFNA.

Experimental studies of the gap structure of BFNA (with the partial substitution of Ni) are scarce and were carried out primarily on optimally doped single crystals with x = 0.1. Data on the number and values of superconducting order parameters obtained by local, bulk, and surface methods [7–13] are poorly consistent: in particular, the characteristic ratio for the large superconducting gap is 2Δ_L(0)/k_BT_c ≈ 3.7–13, i.e., varies by a factor of 3.5. The inconsistency of existing data [7–13] also raises a question of the applicability of some experimental methods to the study of properties of unconventional multiband superconductors with anisotropic order parameters.

It can be expected that the gap structure in the underdoped region of the phase diagram is different from those in other regions because of the possible effect of the antiferromagnetic and nematic phases. However, superconducting order parameters in underdoped BFNA with x < 0.09 have not yet been studied. In this work, we propose a comprehensive multiband approach based on incoherent multiple Andreev reflection (IMARE) spectroscopy and the measurement of the lower critical field H_c1(T), which provides more reliable data on the gap structure of anisotropic superconductors. Using this approach, we determine for the first time the structure of the superconducting order parameter of weakly underdoped BaFe_1.92Ni_0.08As₂ pnictides, including the values, temperature dependences, and characteristic ratios of two superconducting gaps; estimate a moderate anisotropy of A_L ≈ 30% of the large superconducting gap; and conclude that the small gap is highly anisotropic: A_S ≥ 50–100%. The similarities and differences of the gap structures of BFNA pnictides with different degrees of doping are discussed.

2 DETAILS OF THE EXPERIMENT

Large BaFe_1.92Ni_0.08As₂ single crystals up to 1 cm were grown by the “self-flux” technique. The characterization by X-ray diffraction, element analysis, electron microscopy, and resistive and magnetic measurements showed the existence of a single superconducting phase with T_c ≈ 18.5 K and a high degree of homogeneity of crystals. Details of the synthesis and characterization are presented in [14–16] and in Section II of the supplementary material.

Mechanically controlled planar superconductor–thin normal metal–superconductor (SnS) nanojunctions with the current flow direction along the c axis were created in BFNA single crystals using the break-junction technique [17]. Typical current–voltage characteristics of such junctions are shown in Fig. 1а, and the temperature dependence of the resistance near T_c for a 4 × 2 × 0.2-mm platelet single crystal is presented in Fig. 2 (gray circles, right axis). The width of the resistive transition is about 1.1 K. The design of the sample holder, details of the experiment with layered compound samples, and advantages and disadvantages of the method are described in detail in review [18]. The physical model of the junction is schematically shown in [19, Fig. 1]. The controllable parameters of the tunnel junction in the planar break-junction technique experiments are the area of the junction (in the $ab$ plane) and, correspondingly, its normal resistance R_N rather than the thickness and transparency of the constriction (gap, see [18, Figs. 12 and 16] and Section II in the supplementary material).

Fig. 1.

(Color online) Temperature evolution of (а) current–voltage characteristics and (b) $dI(V){\text{/}}dV$ spectra of the SnS junction with T_c ≈ 18.2 K. The normal conductance of the junction is G_N(T, eV > 2Δ) ≈ const; for convenience, lines (except for the black solid and dashed lines) are shifted vertically by $c(T)$, and the dashed line is $dI(V){\text{/}}dV$ at 19.9 K. Vertical lines at 4.2 K mark the fundamental Andreev feature (doublet, n_L = 1) from the large superconducting gap Δ_L ≈ 3.2–4.5 meV (values correspond to the degree of supposed anisotropy), and blue dashes indicate the first and second subharmonics $n_{{\text{L}}}^{{{\text{out}}}} = 1,{\kern 1pt} 2$ from its outer edge $\Delta _{{\text{L}}}^{{{\text{out}}}}$. The violet solid line is the approximation of the shape of the n_L = 1 doublet within the approach proposed in [25]. Arrows mark Andreev minima (n_S = 1, 2) from the small gap Δ_S ≈ 1.6 meV.

Fig. 2.

(Color online) (Upper panel) Temperature dependences of the (filled circles) edges and (empty circles) effective value of the large superconducting gap $\Delta _{{\text{L}}}^{{{\text{in}}{\text{,}}{\kern 1pt} {\text{out}}}}(T)$ and (triangles) the maximum value in the angular distribution of the small gap Δ_S(T) according to the data presented in Fig. 1. The dash-dotted line is the single-band Bardeen–Cooper–Schrieffer-type function, and gray circles indicate the resistive superconducting transition of the bulk BaFe_1.92Ni_0.08As₂ single crystal. The insets show the temperature dependences of the supposed anisotropy of the large gap $A(T) \equiv 100{\kern 1pt} \% \times \;[1 - \Delta _{{\text{L}}}^{{{\text{in}}}}{\text{/}}\Delta _{{\text{L}}}^{{{\text{out}}}}]$ (squares) and the presumed schematic angular distribution Δ_L(θ) in the ${{k}_{x}}{{k}_{y}}$ plane. (Lower panel) Temperature dependences of (stars) the ratio of the large and small superconducting gaps $\Delta _{{\text{L}}}^{{{\text{out}}}}(T){\text{/}}{{\Delta }_{{\text{S}}}}(T)$ and (empty circles) the ratio of the first and second subharmonics ${{V}_{1}}{\text{/}}{{V}_{2}}$ of $\Delta _{{\text{L}}}^{{{\text{out}}}}$indicated in Fig. 1b by blue dashes with the marks $n_{{\text{L}}}^{{{\text{out}}}} = 1, 2$.

Multiple Andreev reflections occur in the SnS junction below T_c. Incoherent Andreev transport at a high-transparency NS interface (barrier parameter $Z \lesssim 0.3$) induces an excess current (compared to the normal-state current–voltage characteristic above T_c) in the current–voltage characteristics of the SnS junction in the entire bias range $eV$. The dynamic conductance in the spectrum in the limit $eV \to 0$ is much higher than the conductance G_N of the SnS junction in the normal state (so-called foot region), whereas the supercurrent branch is absent in this case [20, 21]. A series of features called the subharmonic gap structure) also appear at the positions ${{V}_{n}}$ directly determined by the superconducting gap Δ at any temperatures up to T_c [20–24]:

$${\text{|}}e{{V}_{n}}(T){\text{|}} = 2\Delta (T){\text{/}}n,\quad n = 1, 2, \ldots .$$

(1)

The number n* of observed subharmonic gap structure minima in the dI(V)/dV spectrum of the planar SnS junction is determined by the ratio of the junction dimension d_c and the inelastic scattering length ${{l}_{{\text{c}}}}$ in the c direction: $n\text{*} \approx {{l}_{c}}{\text{/}}{{d}_{c}}$ [19, 21]. The $dI(V){\text{/}}dV$ spectrum of the multigap superconductor will contain the subharmonic gap structure from each gap.

The effect of the angular distribution $\Delta (\theta )$ in the k space on the shape of Andreev minima within the approach proposed in [25] is demonstrated in [18, Fig. 4]. Supposedly, sharp intense subharmonic gap structure dips are expected in the dI(V)/dV spectrum for the isotropic gap, whereas the amplitude of the subharmonic gap structure is suppressed in the case of the nodal order parameter. The subharmonic gap structure dips forming a doublet whose width is determined by the maximum, Δ^out, and maximum, Δⁱⁿ, binding energies of Cooper pairs in the k space are expected for the gap with the extended s-wave symmetry in the $ab$ plane without nodes. The degree of anisotropy is defined below as $A \equiv 100\% \times [1 - {{\Delta }^{{{\text{in}}}}}{\text{/}}{{\Delta }^{{{\text{out}}}}}]$. Within the formalism proposed in [25] and under the assumption of the doublet shape, the effective anisotropic gap at T ≪ T_c is estimated as ${{\Delta }^{{{\text{eff}}}}} \equiv \frac{{\sum\nolimits_{\theta = 0}^{\pi /2} \Delta (\theta )H(2\Delta (\theta ))}}{{\sum\nolimits_{\theta = 0}^{\pi /2} H(2\Delta (\theta ))}}$, where θ is the angle in the ${{k}_{x}}{{k}_{y}}$ plane and H(eV) = G(eV, 4.2 K) – ${{G}_{{\text{N}}}}(eV,{{T}_{{\text{c}}}})$ is the amplitude of details of the extended (doublet) Andreev feature with $n = 1$.

The x and y momentum components of charge carriers in the planar SnS junction can be conserved in the case of ballistic transport in the $ab$ plane, i.e., if the mean free path $l_{{{\text{ab}}}}^{{{\text{el}}}}$ exceeds ${{d}_{{{\text{ab}}}}}$. At the same time, the ${{k}_{z}}$ component can be unconserved because of the “m-ixing” of charge carriers along the current direction. The estimate of the Sharvin resistance ${{R}_{{\text{N}}}} = \sqrt {8{{\rho }_{{{\text{ab}}}}}{{l}_{{{\text{ab}}}}}{\text{/}}(3\pi {{d}_{{{\text{ab}}}}})}$ [26] similar to [7, 8] for the SnS junction with the normal resistance R_N ≈ 65 Ω makes it possible to obtain ${{d}_{{{\text{ab}}}}} \approx 33$ nm and $l_{{{\text{ab}}}}^{{{\text{el}}}}{\text{/}}{{d}_{{{\text{ab}}}}} \approx 2.6$. Thus, the feature of the planar junctions under study is the ballistic transport in the a and b momentum components, whereas inelastic scattering occurs in the c direction. This allows one to obtain some information on the anisotropy of the superconducting gap in the ${{k}_{x}}{{k}_{y}}$ plane.

Briefly speaking, the mechanically controlled planar break-junction technique allows one to locally (within the junction region with a size of about tens of nanometers) and directly determine the magnitudes, temperature dependences, and characteristic ratios of the superconducting order parameters in high resolution and to estimate their anisotropy in the ${{k}_{x}}{{k}_{y}}$ plane [18].

One of the reliable methods of studying features of the macroscopic order parameter in superconductors is the analysis of the temperature dependence of the superfluid density ρ_sc(T) ~ 1/λ²(T), where λ is the London penetration depth. This method makes it possible to indirectly determine the number of superconducting gaps and their magnitudes, as well as to estimate their angular structure in the momentum space. The temperature dependence of ρ_sc can be obtained from the dependence of the lower critical field using the Ginzburg–Landau formula for type-II superconductors

$${{H}_{{{\text{c}}1}}}(T) = {{\phi }_{0}} [\ln (\kappa (T)) + 0.5]{\text{/}}[4{{\mu }_{0}} \pi {{\lambda }^{2}}(T)]$$

(2)

according to the Ginzburg–Landau theory. The lower critical field H_c1 can be determined from magnetization curves using various methods. As known, the magnetization curve at the external field below H_c1 of the superconducting sample is linear with a slope of ‒1/(4π). When the external field reaches H_c1, Abrikosov vortices formed in a type-II superconductor, enter the crystal and effectively reduce the volume of the superconducting phase, and are responsible for the deviation of the magnetization curve from the linear behavior. In this work, magnetization curves were measured using a Hall microsensor [27]. In this method, a 1 × 1 × 0.2‑mm cylindrical sample is placed on the 50 × 50‑μm Hall sensor parallel to the $ab$ plane and the sensor signal is measured as a function of the static external magnetic field applied along the c axis. The anisotropy of the London penetration and, correspondingly, the density of Cooper pairs in the $ab$ plane are integrated into the measured data. This allows the complementary usage of the two methods because IMARE spectroscopy also detects the anisotropy of the gap in the $ab$ plane. We note that the effect of edge defects at the measurement of $M(H)$ curves changes only the absolute value of H_c1(T), whereas the determined parameters of the superconducting state depend only on the shape of the H_c1(T)/H_c1(0) curve. The choice of the criterion of determining H_c1 from magnetization curves also affects only the amplitude of H_c1: the resulting normalized temperature dependences H_c1(T)/H_c1(0) are similar to each other with an error of less than 2%.

To describe the results of the measurement of the lower critical field, the so-called alpha model is commonly used to calculate the macroscopic order parameter of an isotropic superconductor [28]; this model is easily extended for a two-gap superconductor [29]:

$${{\rho }_{{sc}}}(T) = \varphi {{\rho }_{{sc1}}}(T) + (1 - \varphi ){{\rho }_{{sc2}}}(T).$$

(3)

This model describes the normalized density of Cooper pairs of two noninteracting superconducting condensates with the corresponding weights (it is assumed that the temperature dependence of the energy of each gap has the Bardeen–Cooper–Schrieffer form). The normalized superfluid density is related to the critical field as

$$\begin{gathered} {{{\tilde {\rho }}}_{{sc}}}(T) \equiv {{\rho }_{{sc}}}(T){\text{/}}{{\rho }_{{sc}}}(0) = {{H}_{{{\text{c1}}}}}(T){\text{/}}{{H}_{{{\text{c1}}}}}(0) \\ = {{\lambda }^{2}}(0){\text{/}}{{\lambda }^{2}}(T). \\ \end{gathered} $$

(4)

With allowance for anisotropy of both gaps, this model generally has seven free parameters: the lower critical field at zero temperature H_c1(0), critical te-mperature T_c (common for both condensates), characteristic ratios $2\Delta _{{\text{L}}}^{{{\text{out}}}}(0){\text{/}}{{k}_{{\text{B}}}}{{T}_{{\text{c}}}}$ and $2\Delta _{{\text{S}}}^{{{\text{out}}}}(0){\text{/}}{{k}_{{\text{B}}}}{{T}_{{\text{c}}}}$ at T ≪ T_c, the degrees of anisotropy of the gaps A_L and A_S (the angular distribution in the momentum space $\Delta (\theta ) = {{\Delta }^{{{\text{out}}}}}\left[ {1 - \frac{A}{2}(1 - \cos (4\theta ))} \right]$, where θ is the angle in the ${{k}_{x}}{{k}_{y}}$ plane, is taken for the calculations), and the weight contribution φ of one of the effective bands. As a result, several solutions can exist. Using $\Delta _{{\text{L}}}^{{{\text{in}}}}(0)$, $\Delta _{{\text{L}}}^{{{\text{out}}}}(0)$, and Δ_S determined directly by IMARE spectroscopy and the critical temperature, we can reduce the number of free parameters to three: H_c1(0), the weight contribution φ of bands with the small gap, and the small gap anisotropy A_S.

The normalized macroscopic order parameter of the isotropic superconductor in the dirty limit can be estimated by the expression [30]

$${{\tilde {\rho }}_{{sc}}}(T) = \delta (T)\tanh \left( {\frac{{\Delta (T)}}{{2{{k}_{{\text{B}}}}T}}} \right),$$

(5)

where $\delta (T) \equiv \Delta (T){\text{/}}\Delta (0)$. In the case of microscopic order parameter $\Delta (\theta )$ anisotropic in the k space, it is necessary to integrate Eq. (5) over the angle θ. Thus, the temperature dependences of the superconducting gaps Δ_L(T) and Δ_S(T) obtained by IMARE spectroscopy can be used for comparison with the normalized dependence H_c1(T)/H_c1(0). Unlike the alpha model, this approach allows one to take into account the interband interaction, which affects Δ_L(T) and Δ_S(T). Taking into account the angular distribution of microscopic order parameters Δ_L(θ) and Δ_S(θ) and their integral value ${{\Delta }^{{{\text{eff}}}}}$ determined above, we obtain in the two-band approximation

$${{\tilde {\rho }}_{{sc}}}(T) = \varphi \tilde {\rho }_{{\text{S}}}^{{{\text{eff}}}}(T) + (1 - \varphi )\tilde {\rho }_{{\text{L}}}^{{{\text{eff}}}}(T).$$

(6)

3 EXPERIMENTAL DATA AND DISCUSSION

Figure 1 presents the current–voltage characteristics I(V) and $dI(V){\text{/}}dV$ spectra of the SnS junction measured below and above T_c. The current–voltage characteristics are symmetric with respect to $eV = 0$ and show no hysteresis or the supercurrent branch, which excludes the Josephson nature of features observed in $dI(V){\text{/}}dV$. On the contrary, an excess current (compared to the normal $I(V)$ curve at T > T_c) is observed in current–voltage characteristics at T < T_c in the entire $eV$ bias range. At the same time, $dI(V){\text{/}}dV$ spectra in the superconducting state clearly demonstrate a foot at $eV \to 0$ and a series of Andreev minima. These features of current–voltage characteristics and $dI(V){\text{/}}dV$ curves correspond to the IMARE regime and a fairly high transparency of the SnS junction according to all the existing theoretical models of multiple Andreev reflections [20, 21, 23, 24].

At a temperature of 4.2 K, a doublet is observed at bias voltages ${\text{|}}eV{\text{|}} \approx 8.9$ and 6.4 meV. The positions of the minima forming the doublet are inconsistent with Eq. (1) and cannot be interpreted as Andreev subharmonics of the orders $n = 1,\;2$ or $n = 2,\;3$ of the isotropic superconducting gap. Features of $dI(V){\text{/}}dV$ at higher bias voltages are absent; i.e., the linear segment of the spectrum corresponds to energies beyond the gap, where the electron density of states does not have intense peaks. Thus, both minima of the doublet are fundamental n = 1 Andreev features, and their positions are directly determined by the energy parameters $\Delta _{{\text{L}}}^{{{\text{out}}}} \approx 4.5$ meV and $\Delta _{{\text{L}}}^{{{\text{in}}}} \approx 3.2$ meV. The minimum at ${\text{|}}eV{\text{|}} \approx 4.5$ meV corresponds to the second subharmonic from $\Delta _{{\text{L}}}^{{{\text{out}}}}$.

Minima observed at lower bias voltages ${\text{|}}eV{\text{|}} \approx 3.2$ and 1.6 meV (n_S = 1 and 2 in Fig. 1b) are apparently the first and second Andreev features of the subharmonic gap structure of the small gap Δ_S ≈ 1.6 meV. The position of the second subharmonic of $\Delta _{{\text{L}}}^{{{\text{in}}}}$ expected at ${\text{|}}eV{\text{|}} \approx 3.2$ meV coincides with the position of the fundamental dip of Δ_S.

According to ARPES data [3] obtained on Ba-122 family single crystals, the (anisotropic) large superconducting gap assumingly develops on the inner hole cylinder at the Γ point and in electron bands, whereas the small gap develops on the outer Γ cylinder.

The characteristic ratios of the energy parameters are $2\Delta _{{\text{L}}}^{{{\text{out}}}}(0){\text{/}}{{k}_{{\text{B}}}}{{T}_{{\text{c}}}} \approx 5.5$, $2\Delta _{{\text{L}}}^{{{\text{in}}}}(0){\text{/}}{{k}_{{\text{B}}}}{{T}_{{\text{c}}}} \approx 4.1$, and 2Δ_S(0)/k_BT_c ≈ 2 < 3.53 (which is characteristic of a “weak” condensate in the multigap superconductor).

We reproducibly observed such doublets on the $dI(V){\text{/}}dV$ spectra of other SnS junctions obtained in BaFe_1.92Ni_0.08As₂ from the same batch, as well as in overdoped and optimally doped BFNA compounds [7, 8], which could be caused by the anisotropy of the large gap Δ_L in the ${{k}_{x}}{{k}_{y}}$ plane ($\Delta _{{\text{L}}}^{{{\text{out}}}}$ and $\Delta _{{\text{L}}}^{{{\text{in}}}}$ correspond to the maximum and minimum binding energy of Cooper pairs depending on the momentum direction). In favor of this assumption, the shape of the doublet can be approximated within the approach proposed in [25]: the result of the numerical calculation at 4.2 K is shown by the violet solid line in Fig. 1, and the corresponding angular distribution Δ_L(θ) is presented in the upper inset of Fig. 2. At the same time, the existence of two distinct isotropic superconducting gaps $\Delta _{{\text{L}}}^{{{\text{in}}}}$ and $\Delta _{{\text{L}}}^{{{\text{out}}}}$ (developing below T_c on different sheets of the Fermi surface) is not excluded. Since pronounced doublets are not reproducibly observed on spectra for the small gap, one may suppose the small gap Δ_S either isotropic or having a degree of anisotropy higher than 50%, as well as even nodal in the (k_x, k_y) plane. A small amplitude (~0.2G_N) of Andreev minima from the small gap Δ_S can also indicate its strong anisotropy along the ${{k}_{z}}$ direction. In order to distinguish the above-listed cases and to reliably determine the symmetry of Δ_L and Δ_S, the existing theoretical models of multiple Andreev reflection [20, 21, 23, 24] should be extended for the case of the anisotropic superconducting gap and the shape of doublets on $dI(V){\text{/}}dV$ spectra should be examined in more detail.

As the temperature increases, the amplitude of all Andreev minima decreases and their positions are shifted toward zero, reflecting the temperature dependence of the order parameter $\Delta (T)$ according to Eq. (1). At the same time, the excess current at ${\text{|}}eV{\text{|}} > 2{{\Delta }_{{\text{L}}}}$ (Fig. 1a) and the zero bias conduction decrease (Fig. 1b). On the contrary, the normal conductance of the junction at ${\text{|}}eV{\text{|}} > 2{{\Delta }_{{\text{L}}}}$ remains approximately constant (cf. the black solid line at $T = 4.2$ K and the dashed line at T > T_c in the bottom of Fig. 1b at maximum eV values; for convenience, the other $dI(V){\text{/}}dV$ spectra are shifted vertically in the order of increasing temperature), which unambiguously indicates the ballistic transport through this junction. Features caused by Andreev transport are absent in the current–voltage characteristic and the $dI(V){\text{/}}dV$ spectrum (dashed line in Fig. 1b) at T ≈ 18.9 K > T_c, which corresponds to the transition of the junction region in the normal state.

For clarity, the normal-state dynamic conductance, which is reproducibly nonlinear in BFNA SnS junctions and has the shape similar to that presented in [8, Fig. 1], was suppressed for all $dI(V){\text{/}}dV$ spectra in Fig. 1b. This nonlinearity is not due to the overheating of the junction (in this case, the maximum of $dI(V){\text{/}}dV$ at low $eV$ values would observed in the n-ormal state [31]) and can be interpreted as the manifestation of features of the electron density of states near the Fermi level (for more detail, see [8, Section III(a)]).

The temperature dependences of three observed energy gap parameters $\Delta _{{\text{L}}}^{{{\text{out}}}}(T)$, $\Delta _{{\text{L}}}^{{{\text{in}}}}(T)$ (circles), and Δ_S(T) (triangles) in Fig. 2 directly obtained from data in Fig. 1b are typical of the case of the moderate interband interaction. The degree of supposed anisotropy of the large gap is $A(T) \approx 29{\kern 1pt} \% \approx {\text{const}}(T)$ (squares, lower inset of Fig. 2). Although this estimate of anisotropy is indirect, nodes of Δ_L in the k space are certainly absent. The small gap near T_c is closed more rapidly (stars, the lower panel of Fig. 2). Since the ratio Δ_L(T)/Δ_S(T) is not constant and increases at T → T_c, Andreev minima marked in Fig. 1b by n_S = 1 and 2 cannot be interpreted as higher order subharmonics from the large gap Δ_L, therefore, the small gap Δ_S is a distinct superconducting order parameter. The dip indicated in Fig. 1b by the blue vertical straight line with the $n_{{\text{L}}}^{{{\text{out}}}} = 2$ mark is the second subharmonic of $\Delta _{{\text{L}}}^{{{\text{out}}}}$ because it has the bias voltage corresponding to the expected value ${{V}_{2}} = {{V}_{1}}{\text{/}}2$ and the temperature dependence resembling that of $n_{{\text{L}}}^{{{\text{out}}}} = 1$ (blue circles in the lower panel of Fig. 2; see also Section II in the supplementary material).

The magnetization curves of the BaFe_1.92Ni_0.08As₂ single crystal are presented in Fig. 3. The criterion of the determination of H_c1 (disregarding the demagnetization factor) from the dependence $\sqrt {\Delta M(H)}$ (inset of Fig. 3) is typical of measurements with the Hall sensor [32]. The initial horizontal segment in this dependence theoretically corresponds [33] to the Meissner state, whereas the linearly increasing segment corresponds to the mixed state. Experimental $\sqrt {\Delta M(H)}$ curves can demonstrate noises and nonlinearities, which are due in our opinion to small inhomogeneity inclusions of the superconducting phase, which can be located near the sensitive region of the Hall sensor. We reached a very low noise level of 0.02–0.03 Oe (at a sensor sensitivity of 0.5 μV/Oe), which is a factor of about 20 lower than that in [32]. The signal of the Hall sensor exceeding the level of noises and nonlinear parasitic contributions on the $\sqrt {\Delta M(H)}$ dependences was chosen as the criterion of the determination of the lower critical field H_c1 (horizontal straight line in the inset of Fig. 3).

Fig. 3.

(Color online) Magnetic-field dependence of the signal of the Hall sensor at various temperatures. The inset shows $\sqrt {\Delta M(H)}$ curves for temperatures of (blue line) 7 and (brown line) 6 K, where the y = 0 horizontal straight segment corresponds to the Meissner region, whereas the linearly increasing segment approximated by the dashed line corresponds to the mixed state region. The signal level marked by the horizontal straight line, which is above both the noise level and the level of nonlinear parasitic contributions (as seen on the blue line) was the criterion for the determination of H_c1.

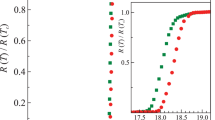
The dependence H_c1(T) obtained from data presented in Fig. 3 and its fits within the two-band alpha model for two cases are shown by red and blue lines in Fig. 4. In both cases, the large gap Δ_L = 3.2–4.5 meV with the degree of anisotropy A_L = 29% and the characteristic small gap Δ_S = 1.6 meV, which were obtained from IMARE spectroscopy data, were taken. In the first case (red lines in Fig. 4), Δ_S is assumed isotropic (A_S = 0). A significant difference between data and model calculations is seen at $T < 10$ K. In this variant, the best approximation is reached at a weight contribution of 82% from bands with the small gap. In the second case (blue lines in Fig. 4), we took an anisotropic small gap, which ensures better agreement between experimental data and calculation at a degree of anisotropy of A_S = 58% and a weight contribution of 62% from bands with the small gap. Under the variation of the criteria for the determination of the lower critical field H_c1 from magnetization curves, the best approximation of H_c1(T) allows the spread of the weight contribution from bands with the small gap within ±5% and the spread of the anisotropy of Δ_S within ±12% from the average A_S = 55%. Approximations of H_c1(T) curves with other criteria are given in the supplementary material.

Fig. 4.

(Color online) (Filled circles) Experimental temperature dependence of the lower critical field H_c1(T) and its approximations by (red lines) the α model with isotropic Δ_S and the weight coefficient $\varphi = 0.28$; (blue lines) the α model with 58% anisotropic Δ_S and the weight coefficient $\varphi = 0.38$; and (right axis, green lines) Eqs. (5) and (6) with 100% anisotropic Δ_S and the weight coefficient $\varphi = 0.6$ (green short dashed line is the contribution of bands with the isotropic small gap Δ_S ≈ 1.6 meV). The deviation of the approximations from experimental data are given in the corresponding colors in the bottom. The dashed and dash-dotted lines are contributions of bands with the small and large gaps (anisotropy A_L = 29%), respectively, whereas the solid lines are the total density of Cooper pairs ρ_sc.

The approximation of the normalized temperature dependence H_c1(T)/H_c1(0) by IMARE spectroscopy data on the microscopic order parameters $\Delta _{{\text{L}}}^{{{\text{eff}}}}(T)$ and $\Delta _{{\text{S}}}^{{{\text{eff}}}}(T)$ is shown by green lines in Fig. 4 (right axis). We note that the critical temperature T_c of the bulk crystal according to magnetization data coincides with the critical temperature T_c of the Andreev junction according to IMARE spectroscopy data. For the case of the isotropic small gap Δ_S ≈ 1.6 meV, the contribution of the corresponding bands to the superfluid density (short dashed line in Fig. 4) begins to sharply decrease at rather high temperatures $T \approx 6$ K; thus, the low-temperature part of the temperature dependence H_c1(T)/H_c1(0) cannot be approximated. Experimental data can generally be described by integrating Eq. (6) over the angle with the weight coefficient $\varphi \approx 0.6$ for bands with the small gap Δ_S under the assumption of its 100% anisotropy (which gives the effective value $\Delta _{{\text{S}}}^{{{\text{eff}}}}(0) \approx 0.8$ meV) (solid green line in Fig. 4).

Thus, the best approximation of H_c1(T) corresponds to the second considered case (blue line in Fig. 4 and the second row in Table 1).

Table 1. Degree of anisotropy of the small superconducting gap A_S, the characteristic ratio for its effective value $2\Delta _{{\text{S}}}^{{{\text{eff}}}}(0){\text{/}}{{k}_{{\text{B}}}}{{T}_{{\text{c}}}}$, and the weight contribution of bands with Δ_S obtained from the approximation of H_c1(T) with different criteria of choosing the H_c1 value in the case of the anisotropic large gap with threshold amplitudes $\Delta _{{\text{L}}}^{{{\text{in}}}} = 3.2$ meV and $\Delta _{{\text{L}}}^{{{\text{out}}}} = 4.5$ meV (anisotropy A_L = 29%)

The comparison of IMARE spectroscopy data with the lower critical field measurements shows that H_c1(T) data cannot be described with the isotropic small gap Δ_S. This indirectly indicates a fairly strong anisotropy of the small gap and that a feature only from the its outer edge $\Delta _{{\text{S}}}^{{{\text{out}}}} \approx 1.6$ meV can be observed in the tunnel experiment.

Since the strong anisotropy of the superconducting gap in the $k$ space can hardly be obtained within the pure ${{s}^{{ + + }}}$ approach [6], spin fluctuations moderately contribute in the superconducting pairing mechanism in underdoped BFNA. Nevertheless, the gap structure of BFNA with x = 0.08 is quite similar to our data on optimally doped and overdoped crystals [7, 8] (except for the strong anisotropy of the small gap Δ_S, which was not observed in our previous works and requires further study). We did not observe a noticeable change in the anisotropy of the large gap Δ_L in a weakly underdoped compound: the value A_L ≈ 30% is in a range of 27–37% estimated for compounds with x = 0.1 and 0.14 [7, 8].

The deviations of three approximations from the experimental data on H_c1(T) are shown in the corresponding colors in Fig. 4. It is seen that all used approaches hardly reproduce experimental data quantitatively in the region of the fast decrease in superfluid density in bands with the small gap Δ_S at T ~ 4 K. It can be assumed that this inconsistency is due either to an increase in the effect of some unincluded channel of inelastic scattering on impurities at these temperatures or to the asymmetry of electron–hole states below T_c in bands with the small gap Δ_S.

4 CONCLUSIONS

A comprehensive approach to the study of the anisotropic superconducting order parameter involving IMARE spectroscopy of planar SnS junctions and the measurement of the lower critical field has been proposed. We have found that the anisotropy of the large superconducting gap (without nodes in the k space) in weakly underdoped BaFe_1.92Ni_0.08As₂ pnictides with T_c ≈ 18.2 K is A_L ≈ 30%. No noticeable difference of the characteristic ratio 2Δ_L(0)/k_BT_c ≈ 4.1–5.7 (range corresponds to A_L) and the degree of anisotropy from the respective parameters in other regions of the phase diagram of BFNA has been observed [7, 8]. Nevertheless, a significant anisotropy of A_S ≈ 50–100% has been found for the small gap by fitting the temperature dependence H_c1(T)/H_c1(0).

The directly measured temperature dependences $\Delta _{{\text{L}}}^{{{\text{in}}{\text{,out}}}}(T)$ and Δ_S(T) are typical of the moderate interband interaction, and the degree of supposed anisotropy of the large gap hardly depends on the temperature.