Multiwell Potential in a Trench-Type Quantum Point Contact

A physical mechanism has been proposed to explain the appearance of the multichannel electron transport regime in trench quantum point contacts. It has been shown that the redistribution of electrons in a two-dimensional electron gas, which is due to the Coulomb interaction between them and with charged donors and X-valley electrons, results in the experimentally observed multichannel regime. The numerical simulation of the redistribution of electrons and its comparison with the measurements of the conductance of trench quantum point contacts based on a GaAs/AlGaAs heterostructure demonstrate the formation of a multiwell confining potential.

1 INTRODUCTION

A characteristic feature of quasi-one-dimensional ballistic transport is the quantization of the conductance, which is manifested as plateaus on the dependence of the conductance of a conductor on its width at values of $N \times 2{{e}^{2}}{\text{/}}h$ ($N = 1,2,3, \ldots$) [1, 2]. A quantum point contact (QPC), which is a microconstriction in a two-dimensional electron gas (2DEG) with a width comparable with the Fermi wavelength of an electron, is a typical structure demonstrating this phenomenon. Quantum point contacts are traditionally fabricated with the split metal gate technology. An alternative method of fabrication of the QPCs is the etching of lithographic trenches, which separate the conducting region from the side gates. The use of trench QPCs, in contrast to structures with a metal gate, allows the application of higher positive and negative voltages on gates. It was previously shown that the application of a potential difference between the gates can induce the spin polarization in a QPC [3–5]. Furthermore, the possibility of varying voltages across side gates independently allows one to study the conductance of the QPC in a wide range of the sum and difference of gate voltages. Such measurements make it possible to detect an extraordinary mode of quantization of the conductance of several conducting channels [6–9]. The formation of several channels inside a single QPC is usually attributed to Wigner crystallization [10–14] and is explained by a structural phase transition occurring in it from a one-dimensional chain of electrons to a correlated double-row zigzag structure (the so-called “zigzag–string” phase transition) [15–17]. Since the motion of electrons is correlated, the conductances of channels in such a double-row Wigner structure are dependent. At the same time, trench QPCs experimentally demonstrate a multichannel regime with an almost independent quantization of the conductances of channels, which cannot be explained by the above Wigner crystallization. This multichannel regime is considered in this work.

The physical mechanism of the multichannel regime is incompletely clear, but we suppose that the multichannel regime in the QPCs based on GaAs/AlGaAs heterostructures is due to the formation of a multiwell confining potential because of the self-consistent redistribution of charges in the heterostructure (Γ-valley electrons in the 2DEG, charged donors, and X-valley electrons localized on them), minimizing the energy of the system. In the context of the minimization of the energy of the system, the effect under consideration is similar to the mentioned zigzag–string transition in the Wigner crystal, but in our case, it primarily concerns charged donors and X electrons. It is important that the cooling of the sample results in the freezing of the formed distribution of charged donors and X electrons, thus fixing the appearing potential for Γ electrons in the 2DEG.

The numerical calculation reported in [18] demonstrates the formation of a double-well potential in the QPC with a metal gate because of the Coulomb interaction of electrons in the 2DEG. However, the channels associated with it are dependent as in the Wigner crystal. In addition, the effect of X electrons and charged donors, as well as the freezing of the potential created by them, was disregarded in that calculation. In this work, we present the numerical simulation of the QPC based on GaAs/AlGaAs heterostructures that demonstrates a physical mechanism of the multichannel regime caused by the redistribution of X electrons and positively charged donors, as well as by the freezing of the potential created by them. The numerical calculations describe the conditions for the formation of the double-, triple-, and generally multiwell confining potentials. We consider two models, one of which involves the redistribution of X electrons, and the other, of positively charged donors. Both models correspond to zero temperature. One of the results of the performed self-consistent calculations is the phase diagram of electrons in the ground state in the QPC, which describes the formation of one, two, and three wells in the confining potential. The calculations are compared with measurements of the conductance of the QPC as a function of the sum and difference of the gate voltages at a temperature of $T = 1.65$ K. These measurements demonstrate that two conducting channels with independently quantized conductances are formed in the QPC. The formation of several channels is independent of the method of cooling of the sample and is reproduced in different cooling cycles.

2 EXPERIMENTAL METHOD

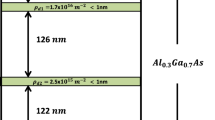
To study the multichannel electron transport regime, we fabricated the QPC based on the GaAs/AlGaAs heterostructure with the 2DEG grown by molecular beam epitaxy on a GaAs substrate (Fig. 1a). This heterostructure is a short-period AlAs/GaAs superlattice with a GaAs layer 13 mm thick, forming a symmetric square potential well for electrons. The doping of the structure with donor Si δ‑layers located symmetrically on both sides of the potential well makes it possible to fill the potential well with electrons, forming the 2DEG. The concentration and mobility of electrons at a temperature of 4.2 K were ${{n}_{{{\text{2D}}}}}$ = (6–7) × 10¹¹ cm^–2 and $\mu = 2 \times {{10}^{6}}$ cm²/(V s), respectively. A feature of used heterostructures is that low-mobility X-valley electrons with a characteristic concentration of ${{n}_{{\text{X}}}} \sim {{10}^{{10}}}$ cm^–2 are also localized on Si donors; these electrons do not contribute to the conductance at low temperatures but smooth fluctuations of the electrostatic potential of impurities, thus increasing the mobility of the 2DEG. Such an application of X electrons was proposed in [19]. The presence of the Al_0.8Ga_0.2As layer between the substrate and superlattice does not affect the discussed experiment. This layer was used to fabricate suspended nanostructures, i.e., nanostructures separated from the substrate [20, 21], but we study an unsuspended structure.

Fig. 1.

(Color online) Layouts of (a) the heterostructure with the 2DEG doped with Si δ-layers (dashed lines) and (b) the trench quantum point contact.

In this work, we study the QPC prepared by the etching of trenches 150 nm wide in the heterostructure, which separated the conducting region from two symmetric side gates (Fig. 1b). Trenches were formed by means of electron lithography and subsequent reactive ion etching. The lithographic width of the QPC was about 900 nm, and the radius of curvature of gates near the QPC was 1 μm.

The conductance of the QPC at various gate voltages ${{V}_{{{\text{G1}}}}}$ and ${{V}_{{{\text{G2}}}}}$ was measured by the synchronous detection of the alternating current ${{I}_{{{\text{AC}}}}}$ flowing through the QPC under the ac voltage with the amplitude ${{V}_{{{\text{AC}}}}} = 100$ μV applied between the source and drain. The measurements were performed in the linear response regime at a temperature of $T = 1.65$ K. The measured conductance is inverse to the total resistance of the QPC and its supplying regions:

$${{G}_{m}} = \frac{{{{I}_{{{\text{AC}}}}}}}{{{{V}_{{{\text{AC}}}}}}} = \frac{1}{{G_{{{\text{QPC}}}}^{{ - 1}} + R}},$$

where G_m is the measured conductance, G_QPC is the conductance of the QPC, and R ≈ 1.6 kΩ is the resistance of supplying regions, which is independent of the gate voltages.

3 RESULTS OF THE EXPERIMENT

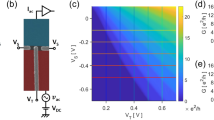
Figure 2a shows a series of curves obtained under the synchronous variation of voltages on side gates. Each curve is the dependence of the conductance on the sum ${{V}_{{{\text{G1}}}}} + {{V}_{{{\text{G2}}}}}$ of voltages applied to the gates at a fixed difference $\Delta {{V}_{{\text{G}}}} = {{V}_{{{\text{G1}}}}} - {{V}_{{{\text{G2}}}}} = {\text{const}}$ between the gate voltages. This difference for all curves is in the range from –10 to +10 V. For a better representation, the curves are shifted with respect to each other along the horizontal by 0.125 V. By numerical dif-ferentiation, we obtained the transconductance $\partial G{\text{/}}\partial ({{V}_{{{\text{G1}}}}} + {{V}_{{{\text{G2}}}}})$ whose distribution in the sum and difference of the gate voltages is shown in Fig. 2b on a black-and-white scale.

Fig. 2.

(Color online) (a) Conductance versus the sum of gate voltages at their fixed difference. The leftmost and rightmost lines correspond to $\Delta {{V}_{{\text{G}}}} = - 10$ and +10 V, respectively. The red arrow marks a half-integer plateau 0.5 × 2e²/h. (b) Distribution of the transconductance $\partial G{\text{/}}\partial ({{V}_{{{\text{G1}}}}} + {{V}_{{{\text{G2}}}}})$ in the sum and difference of the gate voltages. Dark regions correspond to plateaus of the conductance, whereas light regions correspond to the region of increasing conductance. Pairs of integers are the numbers of filled subbands in two individual channels, and their sums are the conductance in units of $2{{e}^{2}}{\text{/}}h$. Color lines separate regions with plateaus of the conductance; lines with an approximately identical slope are given in the same color.

Experimental curves presented in Fig. 2a exhibit plateaus at values multiple to 2e²/h, but the general picture has a more complex form inherent in paired QPCs parallel to each other [22–24]. It is clearly seen that some plateaus are absent and conductance jumps by 4e²/h are observed. For the sake of clarity, the conductances in units of 2e²/h are indicated in Fig. 2a, and lines separating the regions with different conductance plateaus are added (under the passage from one region in Fig. 2a to another through the line, the conductance changes by 2e²/h). These lines are also seen in the transconductance distribution (Fig. 2b). Lines that can be separated into two groups with approximately identical slope form a grid whose cells contain the region of the distribution in Fig. 2b corresponding to a certain conductance plateau. The formation of the grid can be explained by the presence of two conducting channels in the QPC whose conductances are quantized and summed [6, 7, 9]. However, we note that plateaus at large conductances near (5–6) × 2e²/h cannot even be separated by two groups of curves, in contrast to lower lying plateaus. At a large number of filled one-dimensional subbands, the conductance primarily depends on the sum of the gate voltages and depends slightly on their difference. In this respect, the picture becomes similar to a picture of the conductance of the single-channel QPC. This corresponds to the appearance of so-called anticrossings in the transconductance distribution (Fig. 2b), which were observed in [9]. Some curves demonstrate a half-integer conductance plateau at 0.5 × 2e²/h (red arrow in Fig. 2a), which is apparently due to the lateral spin–orbit coupling [4, 5].

The slopes of the lines presented in Fig. 2b are related to the corresponding capacitance coefficients, as described in [9]. Thus, the analysis of these slopes provides an estimate of approximately 250 nm for the distance between the channels.

4 NUMERICAL SIMULATION

A possible reason for the formation of several channels inside a single QPC is the correlated self-consistent redistribution of charges in the conducting channel, as well as charged impurities and X-valley electrons in AlAs/GaAs superlattice layers, caused by their Coulomb interaction. The mechanism of redistribution is schematically illustrated in Fig. 3. The distribution of charges in the channel is also affected by charged surface states on walls of trenches, which is taken into account in the numerical models below by introducing a parabolic confining potential created by them. The doping of the heterostructure by donor Si δ-layers results in the appearance of Γ-valley electrons forming the 2DEG and mentioned X electrons localized on donors. It can be hypothesized that several channels are formed because the distribution of these charges affects the distribution of Γ electrons, which can thereby be redistributed self-consistently and form several channels so that the total electrostatic energy decreases. The described redistribution of charges can occur under the cooling of the sample from room to low temperatures when the distribution of charged Si donors partially screened by X electrons is frozen, thus fixing the formed potential external for Γ electrons. In turn, Γ electrons in the 2DEG remain degenerate and can be redistributed under the action of the field of side gates and carry the electric current. We try to take into account the effect of aforementioned charges by means of self-consistent numerical calculations within two models, one of which involves the redistribution of X electrons, and the other, of positively charged Si donors. As shown below, the calculations within both models demonstrate the formation of the multiwell potential for Γ electrons in the 2DEG.

Fig. 3.

(Color online) (a) (–) Negative charge uniformly distributed in the 2DEG layer and (+) the total positive charge of donors and X electrons in doped δ-layers. (b) Etching of trenches is electrostatically equivalent to the addition of neutral pairs of virtual positive and negative charges in the regions of trenches. Compared to the uniform distribution, this is equivalent to the appearance of additional virtual negative charges in the planes of δ-layers (shown in blue) and additional virtual positive virtual charges in the plane of the 2DEG (given in red). Unlike the depleting effect of surface charges, the indicated charges create an enriching potential near trenches in their layers.

4.1 Inclusion of the Redistribution of X Electrons

In this model, the distribution of Si donors in δ‑layers remains uniform and the interaction between Γ and X electrons located in layers spaced by a distance of s = 30 nm along the growth axis of the heterostructure is taken into account (Fig. 4a). Since the motion along the QPC (y direction) is considered as free, the charge density in this direction is taken to be uniform. Thus, redistribution occurs entirely in the x direction transverse to the QPC, and the charge density element is modeled by a filament of a finite length L. The effect of X electrons expectedly leads to the lateral redistribution of Γ electrons in the 2DEG. Figure 4b schematically presents the distributions of (blue) the positive charge of donors, as well as of the negative charge of (red) X and (green) Γ electrons in donor layers and in the 2DEG layer, respectively. The shown example of the charge redistribution corresponds to the two-channel case. The aim of the self-consistent calculation is to demonstrate the possibility of such a redistribution. Within the model, electrons are distributed in the potential that is the sum of the external confining potential U_ext, which simulates the lithographic boundaries of the QPC and the surface charge collected on them, and the self-consistent potential U_eff[ρ_X(Γ)] created by X(Γ) electrons:

$${{U}_{{{\text{X}}\left( \Gamma \right)}}} = {{U}_{{{\text{ext}}}}} + {{U}_{{{\text{eff}}}}}\left[ {{{\rho }_{{{\text{X}}(\Gamma )}}}} \right].$$

Fig. 4.

(Color online) (a) Schematic arrangement of charges in the heterostructure. (b) Schematic of the charge density distribution. (c) Distributions of (blue line) the self-consistent potential and (green line) the electron density in the 2DEG calculated with the concentrations n_X = 10¹⁰ cm^–2 and n_Γ = 6 × 10¹¹ cm^–2, the width of the quantum point contact of 900 nm, and L = 3 μm. The dash-dotted line marks the lower quantum confinement subband for electrons in the 2DEG.

Here, the subscript X(Γ) marks quantities referring to X(Γ) electrons and the self-consistent potential U_eff[ρ_X(Γ)] is a functional of the density and is given by the expression

$${{U}_{{{\text{eff}}}}}[{{\rho }_{{{\text{X(}}\Gamma {\text{)}}}}}] = e\left( {{{\varphi }_{1}}[{{\rho }_{{{\text{X(}}\Gamma {\text{)}}}}}] + {{\varphi }_{2}}[{{\rho }_{{\Gamma {\text{(X)}}}}}]} \right).$$

(1)

Here, the first term is the potential created by electrons from the layer where the calculation is performed, and the second term is the potential created by electrons from the neighboring layer. They are given by the formulas

$$\begin{gathered} {{\varphi }_{1}}[\rho ](x) = \frac{e}{{4\pi {{\varepsilon }_{0}}\varepsilon }} \\ \times \;\int \rho (x{\kern 1pt} ')\ln \left[ {\frac{{\sqrt {{{{(L{\text{/}}2)}}^{2}} + {{{(x - x{\kern 1pt} ')}}^{2}}} + L{\text{/}}2}}{{\sqrt {{{{(L{\text{/}}2)}}^{2}} + {{{(x - x{\kern 1pt} ')}}^{2}}} - L{\text{/}}2}}} \right]wdx{\kern 1pt} ', \\ \end{gathered} $$

(2)

$$\begin{gathered} {{\varphi }_{2}}[\rho ](x) = \frac{e}{{4\pi {{\varepsilon }_{0}}\varepsilon }} \\ \times \;\int \rho (x{\kern 1pt} ')\ln \left[ {\frac{{\sqrt {{{{(L{\text{/}}2)}}^{2}} + {{{(x - x{\kern 1pt} ')}}^{2}} + {{s}^{2}}} + L{\text{/}}2}}{{\sqrt {{{{(L{\text{/}}2)}}^{2}} + {{{(x - x{\kern 1pt} ')}}^{2}} + {{s}^{2}}} - L{\text{/}}2}}} \right]wdx{\kern 1pt} ', \\ \end{gathered} $$

(3)

where w = 13 nm is the width of the potential well, $1{\text{/}}4\pi {{\varepsilon }_{0}}$ is the coefficient of proportionality in the Coulomb law, ε = 12.88 is the dielectric constant of GaAs, and the integrals are taken over the entire width of the QPC. The electron density was calculated by the successive approximation method. At each iteration, the Schrödinger equation in layers of X and Γ electrons was solved:

$${{\hat {H}}_{{{\text{X(}}\Gamma {\text{)}}}}}\psi = E\psi ,$$

(4)

$${{\hat {H}}_{{{\text{X(}}\Gamma {\text{)}}}}} = - \frac{{{{\hbar }^{2}}\Delta }}{{2{{m}_{{{\text{X(}}\Gamma {\text{)}}}}}}} + {{U}_{{{\text{X(}}\Gamma {\text{)}}}}},$$

where ${{m}_{{{\text{X(}}\Gamma {\text{)}}}}}$ is the effective mass of X(Γ) electrons. The desired electron density in the lower subband was calculated in terms of the wavefunction of the ground state ${{\psi }_{0}}$, which is a solution of Eq. (4):

$${{\rho }_{{{\text{X(}}\Gamma {\text{)}}}}}(x) = {{n}_{{{\text{X(}}\Gamma {\text{)}}}}}{{\left| {{{\psi }_{0}}(x)} \right|}^{2}},$$

(5)

where ${{n}_{{{\text{X(}}\Gamma {\text{)}}}}}$ is the concentration of X(Γ) electrons.

Figure 4c shows the Γ electron density ${{\rho }_{\Gamma }}(x)$ and the corresponding self-consistent potential calculated with the concentrations n_X = 10¹⁰ cm^–2 and n_Γ = 6 × 10¹¹ cm^–2, the width of the QPC of 900 nm, and L = 3 μm, which are close to the respective parameters in the experiment. The inclusion of the interaction of electrons in the 2DEG with X electrons results in the formation of a double-well potential. A voltage applied between the gates will promote an increase in the depth of one of the potential wells; i.e., the number of filled subbands in it and, thereby, the contribution to the conductance from one channel will increase. The distance between the potential wells is about 200 nm (Fig. 4c), which is comparable with the experimentally determined distance between the channels.

4.2 Inclusion of the Redistribution of Charged Si Donors

As described above, the charge density elements are modeled by filaments of a length L and the potentials created by them are specified by Eqs. (2) and (3). However, in contrast to the preceding model, the distribution of charged donors is not treated as uniform and the effect of their distribution on the distribution of Γ electrons in the 2DEG is taken into account. The cooling of the sample can be accompanied by change in the charge of donors, and their density distribution at low temperature corresponds to the minimum electrostatic energy of the system of charges. Since the distribution of charged donors at low temperatures hardly changes (is frozen), their density was specified as an initial condition in the calculation and did not change. We examined various density distributions of Si donors, modeled by steps of the same width with the height $2{{n}_{{\text{d}}}}{\text{/}}L$ (below, blocks), shown in Fig. 5a. The aim of the calculation was to determine how the electrostatic energy depends on the gap width d between donor blocks at various concentrations of charges n_2D = n_e = n_d and different widths W of the QPC to determine the electron density corresponding to the minimum electrostatic energy.

Fig. 5.

(Color online) (a) Studied configurations of the density of Si donors. (b) Total electrostatic energy of the system versus the gap between donor blocks at the width of the quantum point contact W = 450 nm and ${{n}_{{{\text{2D}}}}} = 4 \times {{10}^{{11}}}$ cm^–2. The red line corresponds to one block of donors, which is located in the middle of the quantum point contact, whereas the blue and green lines correspond to two and three donor blocks, respectively. (c) Phase diagram of electrons at the minimum electrostatic energy in (W, ${{n}_{{{\text{2D}}}}}$) coordinates. (d–f) Distributions of the (blue line) self-consistent potential, (green line) electron density, and (light blue line) donor density at the points (d) A, (e) B, and (f) C of the phase diagram. The dash-dotted line marks the lower one-dimensional quantum confinement subband for electrons.

Since the density of donors was fixed, the density was calculated only for Γ electrons distributed in the potential

$${{U}_{{\text{e}}}} = {{U}_{{{\text{ext}}}}} + {{U}_{{{\text{eff}}}}},$$

where U_ext is the external potential, which simulates the lithographic boundaries of the QPC and the surface charge on them and

$${{U}_{{{\text{eff}}}}} = e\left( {{{\varphi }_{1}}\left[ {{{\rho }_{{\text{e}}}}} \right]-{{\varphi }_{2}}\left[ {{{\rho }_{{\text{d}}}}} \right]} \right).$$

Here, φ₁ and φ₂ are the potentials given by Eqs. (2) and (3) and the electron density is calculated by the formula

$${{\rho }_{{\text{e}}}}(x) = {{n}_{{{\text{2D}}}}}{{\left| {{{\psi }_{0}}(x)} \right|}^{2}},$$

where ψ₀(x) is the wavefunction of the ground state that is a solution of the Schrödinger equation

$${{\hat {H}}_{{\text{e}}}}\psi = {{E}_{0}}{{\psi }_{0}},$$

$${{\hat {H}}_{{\text{e}}}} = - \frac{{{{\hbar }^{2}}\Delta }}{{2{{m}_{{\text{e}}}}}} + {{U}_{{\text{e}}}}.$$

The total electrostatic energy was calculated by the formula

$$E = e\int\limits_0^W ({{\rho }_{{\text{e}}}}{{\varphi }_{1}}\left[ {{{\rho }_{{\text{e}}}}} \right] + {{\rho }_{{\text{d}}}}{{\varphi }_{1}}\left[ {{{\rho }_{{\text{d}}}}} \right]$$

$$ - \;{{\rho }_{{\text{e}}}}{{\varphi }_{2}}\left[ {{{\rho }_{{\text{d}}}}} \right] - {{\rho }_{{\text{d}}}}{{\varphi }_{2}}\left[ {{{\rho }_{{\text{e}}}}} \right])Lsdx.$$

The dependence of the energy on the gap width d between donor blocks calculated at the concentration n_2D = 4 × 10¹¹ cm^–2 and the width of the QPC W = 450 nm is shown in Fig. 5b. Because of the effect of the boundaries of the QPC, the energy in the case of one donor block is obviously minimal if donors are concentrated in the middle of the QPC (this value is marked by the red horizontal straight line). It is also seen that these dependences for two and three donor blocks have minima. The energy minimum for the two-block configuration is lower than the minima of the three- and one-block configurations. The electron and donor density profiles shown in Fig. 5e for the same parameters indicate that the minimum electrostatic energy in this case is reached in the case of two channels.

The minimization of the energy described above was performed under the variation of the concentration in the range of (0.5–4) × 10¹¹ cm^–2 and the width of the QPC in the range of 300–600 nm. The result of the calculation is represented in the form of the phase diagram in Fig. 5c. For points A, B, and C of the phase diagram, we plot the electron and donor density distributions and the self-consistent potential with the energy level of the lower subband (Figs. 5d–5f). The results obtained within this model qualitatively describe the modification of the single-well potential for electrons in the 2DEG to double- and triple-well potentials at an increase in the concentration of electrons and the width of the QPC. Furthermore, the distance between the centers of donor blocks calculated at the parameters close to the experimental values (Fig. 5e) is 240 nm, which is close to the experimentally determined distance between channels.

It is also remarkable that peaks in electron density profiles are located near the centers of donor blocks (Figs. 5d–5f). A similar charge distribution in bilayer graphene calculated in [25] has the form of stripes (one-dimensional charge density wave) in the absence of boundaries. Trenches in our case fix the phase of this wave, matching it to the position of trenches. This ensures the reproducibility of the results.

5 CONCLUSIONS

The conductance of a single trench quantum point contact has been studied experimentally. Its dependence on the sum and difference of the gate voltages demonstrates that two electron conducting channels, which make independent contributions to the total conductance, exist in the quantum point contact. The performed model numerical calculations have shown that the multichannel regime can be due to the self-consistent redistribution of electrons in the 2DEG. This redistribution correlates with the distribution of X-valley electrons in superlattice AlAs/GaAs layers and positively charged Si donors in $\delta$-layers and reduces the electrostatic energy. A more detailed calculation including upper-lying subbands is necessary for a more complete quantitative description of the experiment.