INTRODUCTION

In recent years the progress was achieved in obtaining of extremely short pulses of attosecond duration [1, 2]. The studies of the interaction of such pulses with various media have become increasingly relevant [3–6]. In contrast to long multi-cycle pulses, other physical quantities come into play when it comes to few- and subcycle pulses. One of them is the electric area of the electromagnetic pulse, which is defined by the expression [7]:

$${{S}_{E}} = \int\limits_{ - \infty }^{ + \infty } E(t)dt,$$
(1)

where \(E(t)\) is the electric field strength at a given point in space and t is the time. It is worth noting that for the first time the value defined similarly to the expres-sion (1) was used to describe the propagation of extremely short pulses and their impact on multi-level quantum systems in [8–10]. In the case of usual multi-cycle pulses the electric field strength changes its sign many times over the pulse duration, so that the electric area (1) of such pulses is close to zero. However, for subcycle pulses it is possible to obtain pulses with a nonzero electric area. Such pulses are known as unipolar pulses. In recent years, multiple methods have been proposed for obtaining such unipolar pulses in the terahertz and optical ranges, see review [11] and papers [12–20]. Experimentally, unipolar pulses have been obtained quite recently in the terahertz frequency range [21, 22]. It should also be noted that the electric pulse area exhibits a unique property of conservation during one-dimensional propagation [7].

A unique feature of unipolar pulses is their ability to quickly and efficiently transfer the momentum to a quantum system due to the constant sign of the electric field in the pulse. Provided that the duration of a unipolar pulse is much smaller than the characteristic time of the wave packet motion in a quantum system, the effect of such pulses will be completely determined by the electric pulse area [11]. As a result, unipolar pulses can be used for faster and more efficient control of wave packets in matter, than when using multi-cycle bipolar pulses, as well as for accelerating charges and other applications, see review [11] and cited literature. Also, when describing the interaction of unipolar pulses with quantum systems, the standard concepts applicable to the interaction of long multi-cycle pulses become inapplicable because the physics of interaction becomes different if the pulse duration is shorter than the orbital period of an electron in the ground state [11]. Therefore, the results obtained cause further interest in studying the effects associated with the interaction of unipolar pulses with various optical media.

In this paper, the excitation of an extended layer of a two-level medium by a pair of unipolar half-cycle pulses is theoretically studied. In particular, we consider the case when the time delay between exciting pulses is exactly equal to half the period of resonant oscillations of a two-level medium. Under such conditions the second unipolar pulse stops the oscillations of the induced medium polarization left after the first pulse. The paper shows that due to the phenomenon of superradiance of resonant centers in an extended layer of the medium, the reflected field consists of two unipolar pulses of different polarity, following with a significant time delay between them. The effect obtained may be of interest for controlling the shape of subcycle pulses in resonant optical media.

EMISSION OF A STOPPED POLARIZATION PULSE

Previously, the possibility of the optical control of induced polarization in a nonlinear resonant medium for obtaining unipolar and single-cycle pulses was proposed and actively studied, see reviews [11, 23] and the cited literature. The key idea was to use a pair of successive ultrashort excitation pulses acting on resonant atoms in such a way that the first pulse causes oscillations of the induced dipole moment of the atom at its resonant frequency and the second pulse stops these oscillations. To implement such a dynamics, the incident pulses have to satisfy two conditions. First, the duration of each pulse must be much smaller than the period of resonant oscillations, so that the effect on resonant atoms can be approximated as the instantaneous one. Secondly, the delay between pulses must be exactly equal to half the period of resonant oscillations, since only in this case the second pulse completely stops the oscillations of the induced dipole moment. As a result, the emitted field in the far field has the form of a quasi-unipolar pulse.

It seems to be of particular interest to study such radiation not from a single emitter, but from a whole set of such emitters due to the possibility of observing the effects of collective radiation. Indeed, in the case of such coherent control of the radiation of many resonant atoms, the superradiance phenomenon can be observed, when a constructive interference of the radiations of many in-phase oscillating dipoles takes place [24–28]. Depending on the geometry of the problem under consideration, more complex forms of the optical response of the medium may arise as a result [23].

One of the special cases of such collective radiation of stopped polarization was studied earlier, where the generation of a single-cycle THz or optical pulse from a thin layer of a nonlinear resonant medium was considered in the one-dimensional approximation, see review [23] and the cited literature. As shown, the interference of the responses of individual emitters leads to a single-cycle reflected pulse in the near field. In this case, the layer of the medium was assumed to be optically thin, which ensured in-phase radiation from the entire layer when excitation pulses with a plane wavefront were used. The case of an optically extended medium has not been considered before.

In all the works considered, a model medium of two nonlinearly coupled oscillators with strongly different frequencies was used. A real-world example of such a medium is a Raman-active medium, which is often described using the model of nonlinearly coupled electron and nuclear oscillators [29]. At the same time, it is of obvious interest to extend the obtained results to other classical models, for example, standard resonant media with several levels.

In this paper, we consider the radiation of a stopped polarization pulse, firstly, in a two-level system, and secondly, for the case of an optically extended medium. A two-level medium is the most widely used model of a resonant medium, which has been used for the theoretical studies of many optical phenomena [30], including those associated with the action of extremely short pulses on matter [31]. A large layer thickness compared to the wavelength of the resonant transition can make it possible to obtain new effects associated with the interference of secondary waves from individual radiating centers. In particular, it can be expected that the manifestation of the superradiance phenomenon in such a geometry will lead to an amplification of the stopped polarization pulse emitted by resonant centers and to obtaining more complex optical response profiles of the layer.

It is worth addressing the applicability limits of the two-level approximation for description of the interaction of few-cycle and subcycle pulses with a resonant medium. In many atomic gases (helium, atomic hydrogen, etc.) high excited levels lie relatively close to the first excited level, so that the distance between levels rapidly decreases with increasing the principal quantum number. As a result, the contribution of such high excited levels to the polarization oscillations of the medium will only provide a low-amplitude trailing edge, which can be neglected in the first approximation [23]. In addition, the results of the numerical solution of the time-dependent Schrödinger equation showed that the probability of atom ionization by ultrashort pulses in some cases can be extremely small (on the order of 10–11), even though the photon energy exceeds the ionization potential [23]. The two-level approximation will best describe the medium response, if the two quantum levels under consideration are far from the other levels that are not covered by the spectrum of exciting pulses. In this case, the frequency of the resonant transition under consideration lies in the terahertz, far-infrared or mid-infrared range. The fulfillment of the above conditions eventually justifies using the two-level approximation.

PROBLEM STATEMENT

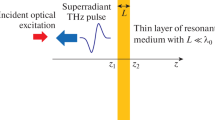
Let us consider an extended layer of a two-level resonant medium excited by a pair of unipolar pulses with a plane wavefront normally incident on the layer (see Fig. 1). The pulses are linearly polarized in the direction orthogonal to the propagation direction. In this layout it is possible to reduce the three-dimensional problem to the one-dimensional one. The layer thickness is assumed to be much greater than the wavelength of the resonant transition in the medium. It is important to note that the problem reduction to a one-dimensional one is justified only if the characteristic transverse dimensions of the system under consideration significantly exceed its longitudinal dimensions, or more precisely, if the distance from the resonant medium layer to the detector is significantly smaller than the diffraction length. Another suitable situation is the pulse propagation in coaxial waveguides, where the possibility of effectively one-dimensional propagation of unipolar pulses was earlier demonstrated [11].

Fig. 1.
figure 1

(Color online) General scheme of the system under consideration: two exciting unipolar pulses following with a time delay \({{T}_{0}}{\text{/}}2\) between them hit an extended layer of a two-level medium.

Full size image

The time delay between both exciting unipolar pulses is chosen to be equal to the half-cycle of the resonant transition in the medium \({{T}_{0}}{\text{/}}2\). In this case such a pair of pulses can effectively control the response of the medium, namely, the first pulse excites oscillations of the medium polarization at the resonant frequency, while the second pulse stops these oscillations [11, 23]. The duration of the exciting pulses should be then much less than the period of the resonant transition in the medium. It should be noted that the effect on the resonant medium will not be altered, if strictly unipolar pulses were replaced by quasi-unipolar pulses that are easier to obtain, while containing a long low-amplitude tail of opposite polarity and having therefore zero electric pulse area (1) [32].

To describe the response of a two-level medium, we will use the standard equations for the density matrix of a resonant medium [33]:

$$\begin{gathered} \frac{{\partial {{\rho }_{{12}}}(z,t)}}{{\partial t}} \\ = - \frac{{{{\rho }_{{12}}}(z,t)}}{{{{T}_{2}}}} + i{{\omega }_{0}}{{\rho }_{{12}}}(z,t) - \frac{i}{\hbar }{{d}_{{12}}}E(z,t)n(z,t), \\ \end{gathered} $$
(2)
$$\begin{gathered} \frac{{\partial n(z,t)}}{{\partial t}} \\ = - \frac{{n(z,t) - {{n}_{0}}(z)}}{{{{T}_{1}}}} + \frac{4}{\hbar }{{d}_{{12}}}E(z,t){\text{Im}}{\kern 1pt} {{\rho }_{{12}}}(z,t), \\ \end{gathered} $$
(3)
$$P(z,t) = 2{{N}_{0}}{{d}_{{12}}}{\text{Re}}{\kern 1pt} {{\rho }_{{12}}},$$
(4)

where P is the polarization of the medium, \({{\rho }_{{12}}}\) is the off-diagonal element of the density matrix of the two-level medium, \(n = {{\rho }_{{11}}} - {{\rho }_{{22}}}\) is the population difference of the two-level medium, \({{N}_{0}}\) is the particle concentration, \({{d}_{{12}}}\) is the transition dipole moment, E is the electric field strength, \({{\omega }_{0}}\) is the resonant transition frequency in the medium (\({{\lambda }_{0}} = 2\pi c{\text{/}}{{\omega }_{0}}\) is the wavelength of the resonant transition), \({{n}_{0}}\) is the equilibrium population difference in the absence of an electric field (\({{n}_{0}} = 1\) for an absorbing medium), \({{T}_{1}}\) is the upper level lifetime, \({{T}_{2}}\) is the relaxation time of the medium polarization, c is the speed of light in vacuum, and \(\hbar \) is the reduced Planck constant.

The equations for the medium have to be supplemented with a one-dimensional wave equation for the electric field:

$$\frac{{\partial E(z,t)}}{{\partial {{z}^{2}}}} - \frac{1}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}E(z,t)}}{{\partial {{t}^{2}}}} = \frac{{4\pi }}{{{{c}^{2}}}}\frac{{{{\partial }^{2}}P(z,t)}}{{\partial {{t}^{2}}}}.$$
(5)

The solution of Eqs. (2)–(5), supplemented by the corresponding initial and boundary conditions, makes it possible to calculate both the field reflected from the layer and the pulse transmitted through the medium.

SIMULATION RESULTS

Equations (2)–(5) were solved numerically by the finite-difference time-domain method (FDTD). Exciting unipolar pulses were taken in the form of Gaussian pulses:

$$E(t) = {{E}_{0}}{{e}^{{ - {{t}^{2}}/\tau _{p}^{2}}}} + {{E}_{0}}{{e}^{{ - {{{(t - {{T}_{0}}/2)}}^{2}}/\tau _{p}^{2}}}},$$

with the pulse amplitude \({{E}_{0}}\) and duration \({{\tau }_{p}}\).

Figure 2 shows an example of a pulse obtained in reflection from the layer. As can be seen from Fig. 2, the reflected field consists of two unipolar half-cycle pulses of opposite polarity separated in time. In between these half-cycle pulses the electric field is close to zero. The parameters of the medium used in the simulation correspond to gaseous media. Of main importance here is the relatively low concentration of active centers, which can easily be achieved in gaseous media, as well as the large values of the relaxation times \({{T}_{1}}\), \({{T}_{2}}\) compared to the resonant transition period in the medium, which also usually takes place in gaseous media. At the same time the exact values of the wavelength or the resonant transition period are not so important, as it is only the exciting pulses being much shorter in duration than the resonant transition period that matters.

Fig. 2.
figure 2

(Color online) Example of a field obtained in reflection from an extended layer of a two-level medium. Parameter values: resonant transition wavelength λ0 = 3 μm (T0 = 10 fs), transition dipole moment \({{d}_{{12}}} = 5{\kern 1pt} \) D, concentration of active centers N0 = 1018 cm–3, medium layer thickness 10 μm, relaxation times \({{T}_{1}} = {{T}_{2}} = 1{\kern 1pt} \) ns, excitation unipolar pulses have a Gaussian shape with duration \({{\tau }_{p}} = 300\) as and the electric field amplitude \({{E}_{0}} = \) 105 ESU.

Full size image

The character of the obtained medium response has a clear physical explanation. The field emitted by each separate two-level center in the layer, as it can be easily shown, represents a single-cycle pulse, i.e., one cycle of a sine wave. This result directly follows from the choice of the time delay between exciting unipolar pulses equal to the half-cycle of the resonant transition \({{T}_{0}}{\text{/}}2\). As a result, the first pulse excites the oscillations of the induced medium polarization at the frequency \({{\omega }_{0}}\), while the second pulse stops these oscillation. This result becomes especially clearly visible, if we plot the instantaneous distribution of the medium polarization \(P(z,t)\) inside the layer at a certain moment of time, when both exciting pulses are inside the medium, see Fig. 3. As can be clearly seen, the polarization distribution is a half-wave sandwiched between two exciting unipolar pulses and propagating along with them. Weak polarization oscillations that remain in the medium after the passage of pulses arise due to the incomplete stop of the medium polarization oscillations by the second unipolar pulse due to its gradual transformation during propagation in the layer. In this case, the field emitted by the resonant centers of the medium in the considered one-dimensional geometry is proportional not to the polarization of the medium itself, but to its first temporal derivative [11, 23]:

$${{E}_{{{\text{rad}}}}}(z,t) - \frac{{2\pi }}{c}\int\limits_{{{z}_{1}}}^{{{z}_{2}}} \frac{{\partial P}}{{\partial t}}\left( {z{\kern 1pt} ',t - \frac{{{\text{|}}z - z{\kern 1pt} '{\text{|}}}}{c}} \right)dz{\kern 1pt} ',$$
(6)

where the spatial integration is taken over the entire thickness of the layer. Except for some deviations during the start and stop of polarization oscillations, the temporal derivative of the medium polarization shown in Fig. 3 represents just one period of the sine wave. Hence, each resonant two-level center inside the layer upon the action of such a pair of unipolar pulses emits a single-cycle pulse at the medium resonant frequency.

Fig. 3.
figure 3

(Color online) Instantaneous distribution of the polarization of the resonant medium inside the layer at some point in time (blue line), as well as the corresponding instantaneous distribution of the electric field (red line). Vertical black dashed lines indicate the boundaries of the resonant medium layer. The system parameters are the same as in Fig. 2.

Full size image

Let us now consider how the interference of waves emitted by individual centers in the layer occurs. At the leading edge of the field reflected from the layer, there will be interference of halfwaves of the same sign out of single-cycle pulses from individual atoms located near the left boundary of the layer in Fig. 1. As a result, we get a constructive interference of such half-waves from individual centers and an intense unipolar half-cycle pulse at the leading edge of the signal reflected from the layer. Another similar unipolar half-cycle pulse, but of opposite polarity, will similarly appear at the trailing edge due to the constructive interference of half-waves of a different sign from single-cycle pulses from individual atoms located near the right boundary of the layer in Fig. 1. In the interval between these two unipolar bursts, half-waves of different signs of the field from different resonant centers in the layer volume will compensate each other, which will lead to a field close to zero. Thus, the field reflected from the layer consists of two time-separated unipolar half-cycle pulses of different field signs, while in the interval between then the field value is close to zero, which corresponds to Fig. 2.

Another physical interpretation of the form of the reflected signal in Fig. 2, based on the spatial distribution of the induced polarization of the medium in Fig. 3 and Eq. (6) for the field emitted by the medium, could be suggested. After the first of the exciting unipolar pulses enters the medium, a monopolar half-cycle pulse of stopped polarization begins to form in the layer, as shown in Fig. 3. At the same time, at the leading edge of this stopped polarization pulse the time derivative of the polarization is positive, so that, according to Eq. (6), the medium layer begins to emit a unipolar burst with a negative field sign, which corresponds to the leading edge of the reflected signal in Fig. 2. By the time the second of the exciting unipolar pulses enters the layer of the medium, a monopolar half-cycle pulse of stopped polarization has already formed in the layer, and at the trailing edge of the stopped polarization pulse, the time derivative of the polarization is negative, as a result, the integral over the layer thickness in (6) becomes zero. In reflection, in this case, a unipolar half-cycle pulse with a negative field sign is formed. Further, while both exciting unipolar pulses propagate inside the layer, the polarization distribution in the layer has the form, as shown in Fig. 3. In this time interval, the radiation from those parts of the layer where the induced polarization increases with time is completely compensated by the radiation from those parts where the induced polarization decreases with time. As a result, the integral in Eq. (6), and hence the field in the reflected signal, vanishes. Finally, after the first excitation pulse leaves the medium, the monopolar half-period pulse of stopped polarization also begins to disappear. In this case, the trailing edge of the stopped polarization pulse with a negative time derivative of the polarization will prevail, so that in the reflected field, according to (6), a unipolar half-cycle burst with a positive field sign similarly appears.

The above qualitative considerations can be supplemented by more rigorous theoretical calculations. We assume that each individual two-level center in the layer emits a single-cycle pulse:

$$E(z,t) = {{A}_{0}}\sin {{\omega }_{0}}t, \quad \frac{z}{c} \leqslant t \leqslant \frac{z}{c} + {{T}_{0}},$$
(7)

where for simplicity the amplitude of the emitted pulse \({{A}_{0}}\) is assumed to be constant over the entire volume of the layer, which is justified at a sufficiently low concentration of resonant centers. If we assume that the left boundary of the layer corresponds to \(z = 0\), as shown in Fig. 3, then the resonant center, located at the point with the coordinate z, starts emitting a single-cycle pulse (7) at the moment \(z{\text{/}}c\), when the first excitation pulse reaches it, and stops after one full period of oscillations at the resonant frequency, i.e., at the time point \(z{\text{/}}c + {{T}_{0}}\). The total radiation from the entire medium layer is expressed in this case by the integral:

$$E(t) = \int\limits_0^L {{N}_{0}}E(z,t)dz.$$
(8)

Here it is assumed that the reflected field \(E(t)\) is measured directly near the left boundary of the layer in Fig. 1 starting from the moment, when the first of the excitation pulses enters the medium. In particular, for \(0 \leqslant t \leqslant {{T}_{0}}\) integral (8) is reduced to the following form:

$$E(t) = \int\limits_0^{ct/2} {{N}_{0}}{{A}_{0}}\sin {{\omega }_{0}}\left( {t - \frac{{2z}}{c}} \right)dz$$
$$ = {{N}_{0}}{{A}_{0}}\frac{c}{{2{{\omega }_{0}}}}(1 - \cos {{\omega }_{0}}t),$$

i.e., we get a unipolar half-cycle pulse at the leading edge of the signal reflected from the layer. Similarly, it is shown that exactly the same unipolar half-cycle pulse, but of opposite polarity, is formed at the trailing edge of the signal reflected from the layer. Finally, let us consider the field in the central part of the reflected signal, i.e., at \({{T}_{0}} \leqslant t \leqslant 2L{\text{/}}c\). In this case, expres-sion (8) gives:

$$E(t) = \int\limits_{c(t - {{T}_{0}})/2}^{ct/2} {{N}_{0}}{{A}_{0}}\sin {{\omega }_{0}}\left( {t - \frac{{2z}}{c}} \right)dz = 0,$$

i.e., the radiation of individual resonant centers in the volume of the layer completely compensate each other, which leads to a zero value of the field.

Strictly speaking, the zero field in the central part of the reflected signal is obtained only when neglecting the change of the exciting pulses as they propagate inside the layer; i.e., if all two-level centers are excited by exactly the same pulses. Such an approximation, however, is justified only if the emitted field is much weaker than the field of exciting pulses, which can be achieved by reducing the concentration of resonant centers in the bulk of the layer. A change in the exciting pulses during propagation inside the layer leads, on the one hand, to a nonzero field in the central part of the reflected signal, and, on the other hand, to the presence of weakly damped oscillations right after the second half-cycle burst due to the incomplete stop of the oscillations of the induced medium polarization, as can be seen in Fig. 2.

The described nature of the constructive interference of the emitted secondary waves allows us to speak about the manifestation of the superradiance effect in the system under consideration. It should be noted that the term “superradiance” itself is now interpreted in a rather broad sense and is used to describe phenomena of various nature, for which the phased coherent radiation of an ensemble of dipole oscillators plays a fundamental role [28]. In our case, the radiation of individual resonant centers in the medium in the approximation of a sufficiently low volume concentration of centers will be coherent with each other, which allows us to talk about the phenomenon of superradiance in such a broad interpretation. The amplitude of the electric field of the generated unipolar pulses in this case will be proportional to the volume concentration of resonant centers. In this case, in contrast to the mechanism of collective spontaneous emission of a concentrated ensemble of dipole oscillators, which was originally described by Dicke [24], where the duration of emission is inversely proportional to the number of excited dipoles, in our system the duration of the resulting unipolar pulses does not almost depend on the volume concentration of resonant centers. It is also important that the characteristic coherence relaxation time in a two-level medium \({{T}_{2}}\) (transverse relaxation time) is much longer than the period of resonant oscillations \({{T}_{0}}\), so that the dephasing mechanisms of individual emitters that appear in the medium do not significantly affect the response of the medium layer.

The demonstrated effect is of interest primarily as one of the manifestations of the phenomenon of superradiance in resonant media, leading to the production of subcycle pulses. In addition, the proposed scheme can also be used to obtain unipolar pulses of various shapes. For example, the possibility of controlling the shape of reflected pulses can be achieved by creating a certain profile of the volume concentration of resonant centers along the length of the extended layer.

CONCLUSIONS

The paper is devoted to a new approach for obtaining unipolar pulses in resonant media, based on the superradiance phenomena. This approach makes use of the stopped polarization superradiance from an extended layer of a two-level resonant medium excited by a sequence of two unipolar pulses. Exciting pulses cause oscillations of the induced medium polarization and the delay between pulses is chosen so that the second pulse stops these oscillations. As a result, it is possible to generate two unipolar bursts of the electric field of different polarity and separated in time due to the constructive interference of the secondary waves emitted by the medium. The proposed method is applicable to radiation both in the terahertz and in the far- or even mid-infrared range.